19.2.3 平行四边形的判定 课件(共26张PPT)
文档属性
| 名称 | 19.2.3 平行四边形的判定 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 19:58:46 | ||
图片预览







文档简介
(共26张PPT)
第
3
课时
平行四边形的判定
沪科版·八年级数学下册
上课课件
第19章
四边形
学习目标
【知识与技能】
1.在探索平行四边形的判别条件中,理解并掌握用边、对角线来判定平行四边形的方法.
2.会综合运用平行四边形的判定方法和性质来解决问题.
3.培养用类比、逆向联想及运动的思维方法来研究问题.
【过程与方法】
经历平行四边形判定条件的探索过程,发展学生的合情推理意识和表述能力.
【情感态度】
培养学生合情推理能力,以及严谨的书写表达,体会几何思维的真正内涵.
【教学重点】
理解和掌握平行四边形的判定定理.
【教学难点】
几何推理方法的应用.
新课导入
平行四边形的定义:
两组对边_________的四边形叫做平行四边形.
性质1
平行四边形的_________.
性质2
平行四边形的_________.
分别平行
对边相等
对角相等
性质3
平行四边形的_______________.
对角线互相平分
新课推进
莉莉手中有一些木条,她想通过适当的测量、割剪,钉制一个平行四边形框架,你能帮她想出一些办法来吗?
取两根等长的木条AB,CD,将它们平行放置,再用两根木条BC,AD加固,得到的四边形ABCD是平行四边形吗?
A
B
C
D
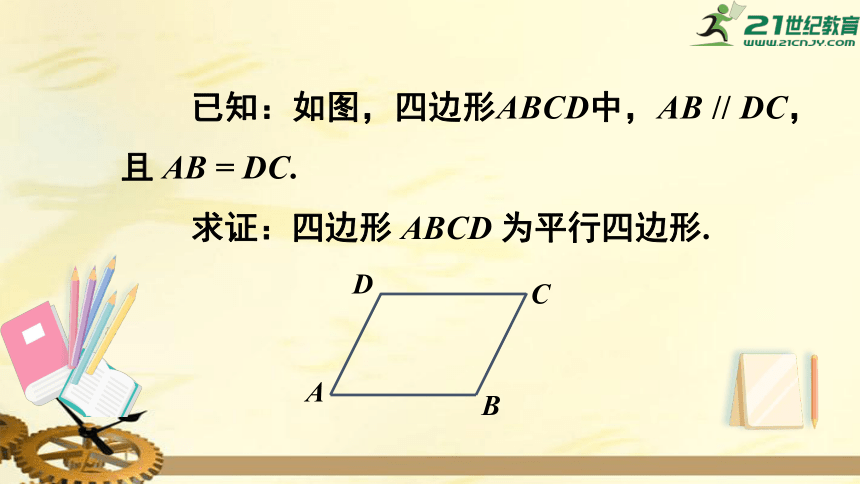
已知:如图,四边形ABCD中,AB
//
DC,且
AB
=
DC.
求证:四边形
ABCD
为平行四边形.
A
B
C
D
证明:连接
AC.
∵
AB
//
DC,
∴
∠BAC
=∠DCA.
又
AB
=
CD,AC
=
CA,
∴
△ABC
≌
△CDA.
∴∠ACB
=
∠CAD.
∴
AD
//
BC.
因此,四边形ABCD是平行四边形.
A
B
C
D
一组对边___________的四边形是平行四边形.
平行四边形判定定理
1
平行且相等
常用符号“____”表示“平行且相等”,
//
=
//
=
“AB
CD”读作“_________________”.
AB平行且等于CD
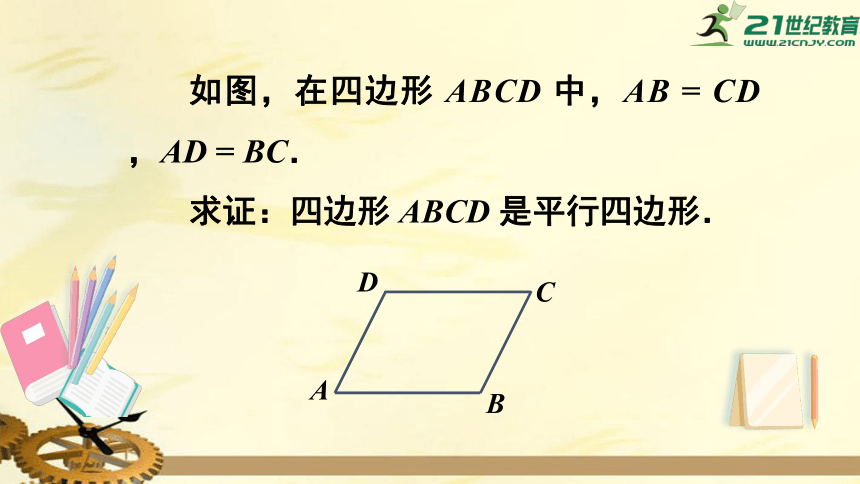
如图,在四边形
ABCD
中,AB
=
CD,AD
=
BC.
求证:四边形
ABCD
是平行四边形.
A
B
C
D
证明:连接BD.
∵ AB=CD,AD=BC,BD是公共边,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形.
D
A
B
C
1
2
3
4
两组对边__________的四边形是平行四边形.
平行四边形判定定理
2
分别相等
如图,在四边形
ABCD
中,
AC,BD
相交于点
O,且
OA
=
OC,OB
=
OD.求证:四边形
ABCD
是平行四边形.
D
A
B
C
O
证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴ △AOD≌△COB.
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形.
D
A
B
C
O
对角线__________的四边形是平行四边形.
平行四边形判定定理
3
互相平分
例5
已知:如图,点
E,F
是
ABCD
的对角线
AC
上的两点,且
AE
=
CF.
求证:四边形
BEDF
是平行四边形.
A
B
C
D
E
F
A
B
C
D
E
F
证明
连接
BD
交
AC
于点
O.
O
因为四边形
ABCD
是平行四边形,所以
AO
=
CO,BO
=
DO.
∵
AE
=
CF.
∴
OE=AO-AE=CO-CF=OF.
所以四边形
BEDF
是平行四边形.
随堂练习
1.四边形ABCD中,已知AB∥CD,再添加一个条件___________,使四边形ABCD是平行四边形.
AB=CD
2.下列条件中,能判定四边形ABCD是平行四边形的是(
)
A.
AB∥CD,AD=BC
B.∠A=∠B,∠C=∠D
C.
AB=CD,AD=BC
D.
AB=AD,CB=CD
C
3.如图,□ABCD
中,线段
EF、GH
分别在AB、CD
上运动,在运动过程中总是保持
EF
=
GH.
(1)试猜想四边形
EFGH
的形状,并说明理由.
解:四边形EFGH为平行四边形.
由平行四边形的性质得:AB∥CD,即
EF∥GH,又∵EF
=
GH,
∴四边形
EFGH
为平行四边形.
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
(2)若
EF=
AB,且S
ABCD
=
24,
则
S四边形EFGH
=____.
8
4.
如图,在
ABCD
中,BD
是它的一条对角线,过
A,C
两点分别作
AE⊥BD,CF⊥BD,E,F
为垂足.求证:四边形
AFCE
是平行四边形.
证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,∴∠ADE=∠CBF,
又∠AED=∠CFB=90°,∴△AED≌△CFB,
∴AE=CF.
又∵
∠AEF=∠CFE=90°,
∴
AE∥CF,
∴四边形AFCE是平行四边形.
平行四边形的
3
种判定方法:
课堂小结
③对角线互相平分的四边形是平行四边形.
①一组对边平行且相等的四边形是平行四边形;
②两组对边分别相等的四边形是平行四边形;
课后作业
1.从教材习题中选取.
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第
3
课时
平行四边形的判定
沪科版·八年级数学下册
上课课件
第19章
四边形
学习目标
【知识与技能】
1.在探索平行四边形的判别条件中,理解并掌握用边、对角线来判定平行四边形的方法.
2.会综合运用平行四边形的判定方法和性质来解决问题.
3.培养用类比、逆向联想及运动的思维方法来研究问题.
【过程与方法】
经历平行四边形判定条件的探索过程,发展学生的合情推理意识和表述能力.
【情感态度】
培养学生合情推理能力,以及严谨的书写表达,体会几何思维的真正内涵.
【教学重点】
理解和掌握平行四边形的判定定理.
【教学难点】
几何推理方法的应用.
新课导入
平行四边形的定义:
两组对边_________的四边形叫做平行四边形.
性质1
平行四边形的_________.
性质2
平行四边形的_________.
分别平行
对边相等
对角相等
性质3
平行四边形的_______________.
对角线互相平分
新课推进
莉莉手中有一些木条,她想通过适当的测量、割剪,钉制一个平行四边形框架,你能帮她想出一些办法来吗?
取两根等长的木条AB,CD,将它们平行放置,再用两根木条BC,AD加固,得到的四边形ABCD是平行四边形吗?
A
B
C
D
已知:如图,四边形ABCD中,AB
//
DC,且
AB
=
DC.
求证:四边形
ABCD
为平行四边形.
A
B
C
D
证明:连接
AC.
∵
AB
//
DC,
∴
∠BAC
=∠DCA.
又
AB
=
CD,AC
=
CA,
∴
△ABC
≌
△CDA.
∴∠ACB
=
∠CAD.
∴
AD
//
BC.
因此,四边形ABCD是平行四边形.
A
B
C
D
一组对边___________的四边形是平行四边形.
平行四边形判定定理
1
平行且相等
常用符号“____”表示“平行且相等”,
//
=
//
=
“AB
CD”读作“_________________”.
AB平行且等于CD
如图,在四边形
ABCD
中,AB
=
CD,AD
=
BC.
求证:四边形
ABCD
是平行四边形.
A
B
C
D
证明:连接BD.
∵ AB=CD,AD=BC,BD是公共边,
∴ △ABD≌△CDB.
∴ ∠1=∠2,∠3=∠4.
∴ AB∥DC,AD∥BC.
∴ 四边形ABCD是平行四边形.
D
A
B
C
1
2
3
4
两组对边__________的四边形是平行四边形.
平行四边形判定定理
2
分别相等
如图,在四边形
ABCD
中,
AC,BD
相交于点
O,且
OA
=
OC,OB
=
OD.求证:四边形
ABCD
是平行四边形.
D
A
B
C
O
证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴ △AOD≌△COB.
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形.
D
A
B
C
O
对角线__________的四边形是平行四边形.
平行四边形判定定理
3
互相平分
例5
已知:如图,点
E,F
是
ABCD
的对角线
AC
上的两点,且
AE
=
CF.
求证:四边形
BEDF
是平行四边形.
A
B
C
D
E
F
A
B
C
D
E
F
证明
连接
BD
交
AC
于点
O.
O
因为四边形
ABCD
是平行四边形,所以
AO
=
CO,BO
=
DO.
∵
AE
=
CF.
∴
OE=AO-AE=CO-CF=OF.
所以四边形
BEDF
是平行四边形.
随堂练习
1.四边形ABCD中,已知AB∥CD,再添加一个条件___________,使四边形ABCD是平行四边形.
AB=CD
2.下列条件中,能判定四边形ABCD是平行四边形的是(
)
A.
AB∥CD,AD=BC
B.∠A=∠B,∠C=∠D
C.
AB=CD,AD=BC
D.
AB=AD,CB=CD
C
3.如图,□ABCD
中,线段
EF、GH
分别在AB、CD
上运动,在运动过程中总是保持
EF
=
GH.
(1)试猜想四边形
EFGH
的形状,并说明理由.
解:四边形EFGH为平行四边形.
由平行四边形的性质得:AB∥CD,即
EF∥GH,又∵EF
=
GH,
∴四边形
EFGH
为平行四边形.
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
(2)若
EF=
AB,且S
ABCD
=
24,
则
S四边形EFGH
=____.
8
4.
如图,在
ABCD
中,BD
是它的一条对角线,过
A,C
两点分别作
AE⊥BD,CF⊥BD,E,F
为垂足.求证:四边形
AFCE
是平行四边形.
证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,∴∠ADE=∠CBF,
又∠AED=∠CFB=90°,∴△AED≌△CFB,
∴AE=CF.
又∵
∠AEF=∠CFE=90°,
∴
AE∥CF,
∴四边形AFCE是平行四边形.
平行四边形的
3
种判定方法:
课堂小结
③对角线互相平分的四边形是平行四边形.
①一组对边平行且相等的四边形是平行四边形;
②两组对边分别相等的四边形是平行四边形;
课后作业
1.从教材习题中选取.
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
