19.3.1.1 矩形的性质 课件(共27张PPT)
文档属性
| 名称 | 19.3.1.1 矩形的性质 课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 20:10:44 | ||
图片预览








文档简介
(共27张PPT)
19.3
矩形、菱形、正方形
1.
矩形
第
1
课时
矩形的性质
沪科版·八年级数学下册
上课课件
学习目标
【知识与技能】
1.掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系.
2.会初步运用矩形的概念和性质来解决有关问题.
【过程与方法】
经历探索矩形的概念和性质的过程,发展学生合情推理的意识;掌握几何思维方法.并渗透运动联系、从量变到质变的观点.
【情感态度】
培养严谨的推理能力,以及自主合作的精神,体会逻辑推理的思维价值.
【教学重点】
矩形的性质.
【教学难点】
矩形的性质的灵活应用.
新课导入
电脑,pad的显示屏是什么形状?
推进新课
矩形是常见的图形,门窗框、皮箱、扑克牌等都有矩形的形象.
你还能举出一些例子吗?
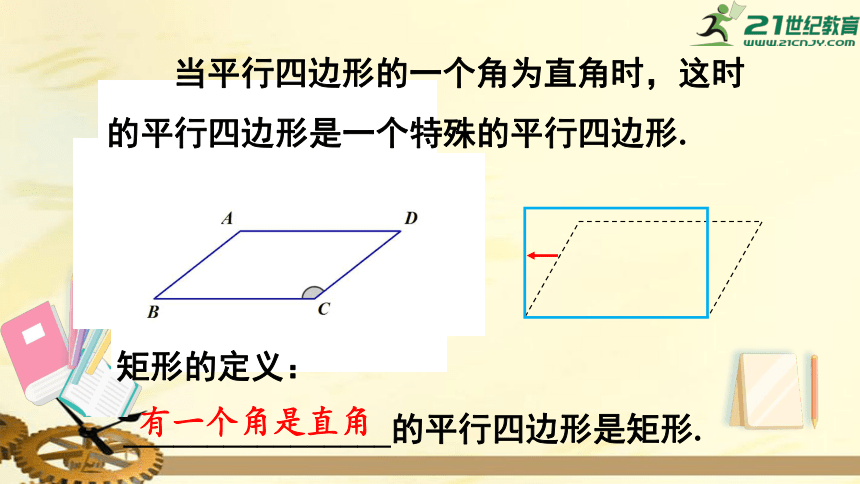
当平行四边形的一个角为直角时,这时的平行四边形是一个特殊的平行四边形.
________________的平行四边形是矩形.
矩形的定义:
有一个角是直角
矩形是特殊的平行四边形,所以它具有平行四边形的所有性质.
1
对边平行且相等
2
对角相等
3
对角线互相平分
因为矩形是平行四边形,所以它具有平行四边形的所有性质.由于它有一个角为直角,它是否具有一般平行四边形不具有的一些性质呢?
思
考
猜想1:矩形的四个角都是______.
直角
猜想2:矩形的对角线______.
相等
命题1:矩形的四个角都是直角.
已知:如图,四边形
ABCD
是矩形.
求证:∠A
=∠B
=∠C
=∠D
=
90°.
A
B
C
D
证明
由定义,矩形必有一个角是直角,设∠A
=
90°.
∵
AB
//
DC,AD
//
BC,
∴
∠B
=∠C
=∠D
=
90°.
(两直线平行,同旁内角互补)
即矩形
ABCD
的四个角都是直角.
A
B
C
D
已知:如图,四边形
ABCD
是矩形,
求证:AC
=
BD.
A
B
C
D
证明:在矩形ABCD中
∵∠ABC
=
∠DCB
=
90°
又∵AB
=
DC
,
BC
=
CB.
∴△ABC≌△DCB(SAS).
∴AC
=
BD,
即矩形的对角线相等.
命题2:矩形的对角线相等
小结
矩形的性质:
(1)矩形的四个角都是______;
(2)矩形的对角线______.
直角
相等
矩形具有而一般平行四边形不一定具有的性质是(
)
A.对边相等
B.对角相等
C.对角互补
D.对角线互相平分
C
练习
已知:在
Rt△ABC
中,∠ABC
=
90°,BO
是
AC
上的中线.
求证:
BO
=
AC.
A
B
C
O
A
B
C
O
证明
延长
BO
至
D,使OD
=
BO,,连结
AD,DC.
D
∵
AO
=
OC,BO
=
OD.
∴
四边形ABCD是平行四边形.
∵
∠ABC=90°.
∴
ABCD是矩形.
∴
AC
=
BD.
∴
BO
=
BD
=
AC.
矩形性质的推论
推论:直角三角形斜边上的中线等于_____________.
斜边的一半
A
B
C
O
例1 如图,矩形
ABCD
的两条对角线
AC,BD
相交于点
O,∠AOB
=
120°,AD
=
4
cm
.求矩形对角线的长.
D
A
B
C
O
∴AC
与
BD
相等且互相平分.
∴OA
=
OB
=
OC
=
OD,
∵∠AOB
=
120°.
解:∵四边形
ABCD
是矩形.
∴
∠OAB
=
∠OBA
=
=
30°.
在
Rt△ABD
中,有
BD
=
2AD
=
2×4
=
8(cm).
随堂练习
1.
矩形的一内角平分线把矩形的一边分成
3
cm
和
5
cm
的两部分,则此矩形的周长为(
)
A.
16
cm
B.
22
cm
C.
26
cm
D.
22
cm
或
26
cm
D
2.
矩形
ABCD
对角线
AC,BD
相交于点
O,AB
=
5
cm,BC
=
12
cm,则
△ABO
的周长等于________.
18
cm
3.
四边形
ABCD
是矩形
(1)若已知
AB
=
8
cm,AD
=
6
cm,
则AC
=____cm,
OB
=___cm.
(2)若已知
AC
=
10
cm,BC
=
6
cm,则矩形的周长
=____
cm,矩形的面积
=____cm2.
10
5
28
48
4.
已知:如图,矩形
ABCD
中,E
是
BC
上一点,DF⊥AE
于
F,若
AE
=
BC.
求证:CE
=
EF.
A
B
C
D
E
F
分析
CE,EF
分别是
BC,AE
等线段上的一部分,若
AF
=
BE,则问题解决,而证明
AF
=
BE,只要证明
△ABE
≌
△DFA
即可,在矩形中容易构造全等的直角三角形.
A
B
C
D
E
F
证明:∵四边形ABCD是矩形,
∴∠B
=90°,且AD∥BC.
∴∠1=∠2,
∵DF⊥AE,
∴∠AFD
=
90°.
∴∠B
=∠AFD.又
AD
=
AE
=
BC,
∴△ABE
≌
△DFA(AAS).
∴AF
=
BE.
∴AE-AF
=
BC-BE
∴EF
=
EC.
A
B
C
D
E
F
∠1
∠2
矩形的四个角都是直角.
矩形的两条对角线相等.
直角三角形斜边上的中线等于斜边的一半.
矩形的性质
1
2
矩形性质推论
课堂小结
课后作业
1.从教材习题中选取.
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
19.3
矩形、菱形、正方形
1.
矩形
第
1
课时
矩形的性质
沪科版·八年级数学下册
上课课件
学习目标
【知识与技能】
1.掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系.
2.会初步运用矩形的概念和性质来解决有关问题.
【过程与方法】
经历探索矩形的概念和性质的过程,发展学生合情推理的意识;掌握几何思维方法.并渗透运动联系、从量变到质变的观点.
【情感态度】
培养严谨的推理能力,以及自主合作的精神,体会逻辑推理的思维价值.
【教学重点】
矩形的性质.
【教学难点】
矩形的性质的灵活应用.
新课导入
电脑,pad的显示屏是什么形状?
推进新课
矩形是常见的图形,门窗框、皮箱、扑克牌等都有矩形的形象.
你还能举出一些例子吗?
当平行四边形的一个角为直角时,这时的平行四边形是一个特殊的平行四边形.
________________的平行四边形是矩形.
矩形的定义:
有一个角是直角
矩形是特殊的平行四边形,所以它具有平行四边形的所有性质.
1
对边平行且相等
2
对角相等
3
对角线互相平分
因为矩形是平行四边形,所以它具有平行四边形的所有性质.由于它有一个角为直角,它是否具有一般平行四边形不具有的一些性质呢?
思
考
猜想1:矩形的四个角都是______.
直角
猜想2:矩形的对角线______.
相等
命题1:矩形的四个角都是直角.
已知:如图,四边形
ABCD
是矩形.
求证:∠A
=∠B
=∠C
=∠D
=
90°.
A
B
C
D
证明
由定义,矩形必有一个角是直角,设∠A
=
90°.
∵
AB
//
DC,AD
//
BC,
∴
∠B
=∠C
=∠D
=
90°.
(两直线平行,同旁内角互补)
即矩形
ABCD
的四个角都是直角.
A
B
C
D
已知:如图,四边形
ABCD
是矩形,
求证:AC
=
BD.
A
B
C
D
证明:在矩形ABCD中
∵∠ABC
=
∠DCB
=
90°
又∵AB
=
DC
,
BC
=
CB.
∴△ABC≌△DCB(SAS).
∴AC
=
BD,
即矩形的对角线相等.
命题2:矩形的对角线相等
小结
矩形的性质:
(1)矩形的四个角都是______;
(2)矩形的对角线______.
直角
相等
矩形具有而一般平行四边形不一定具有的性质是(
)
A.对边相等
B.对角相等
C.对角互补
D.对角线互相平分
C
练习
已知:在
Rt△ABC
中,∠ABC
=
90°,BO
是
AC
上的中线.
求证:
BO
=
AC.
A
B
C
O
A
B
C
O
证明
延长
BO
至
D,使OD
=
BO,,连结
AD,DC.
D
∵
AO
=
OC,BO
=
OD.
∴
四边形ABCD是平行四边形.
∵
∠ABC=90°.
∴
ABCD是矩形.
∴
AC
=
BD.
∴
BO
=
BD
=
AC.
矩形性质的推论
推论:直角三角形斜边上的中线等于_____________.
斜边的一半
A
B
C
O
例1 如图,矩形
ABCD
的两条对角线
AC,BD
相交于点
O,∠AOB
=
120°,AD
=
4
cm
.求矩形对角线的长.
D
A
B
C
O
∴AC
与
BD
相等且互相平分.
∴OA
=
OB
=
OC
=
OD,
∵∠AOB
=
120°.
解:∵四边形
ABCD
是矩形.
∴
∠OAB
=
∠OBA
=
=
30°.
在
Rt△ABD
中,有
BD
=
2AD
=
2×4
=
8(cm).
随堂练习
1.
矩形的一内角平分线把矩形的一边分成
3
cm
和
5
cm
的两部分,则此矩形的周长为(
)
A.
16
cm
B.
22
cm
C.
26
cm
D.
22
cm
或
26
cm
D
2.
矩形
ABCD
对角线
AC,BD
相交于点
O,AB
=
5
cm,BC
=
12
cm,则
△ABO
的周长等于________.
18
cm
3.
四边形
ABCD
是矩形
(1)若已知
AB
=
8
cm,AD
=
6
cm,
则AC
=____cm,
OB
=___cm.
(2)若已知
AC
=
10
cm,BC
=
6
cm,则矩形的周长
=____
cm,矩形的面积
=____cm2.
10
5
28
48
4.
已知:如图,矩形
ABCD
中,E
是
BC
上一点,DF⊥AE
于
F,若
AE
=
BC.
求证:CE
=
EF.
A
B
C
D
E
F
分析
CE,EF
分别是
BC,AE
等线段上的一部分,若
AF
=
BE,则问题解决,而证明
AF
=
BE,只要证明
△ABE
≌
△DFA
即可,在矩形中容易构造全等的直角三角形.
A
B
C
D
E
F
证明:∵四边形ABCD是矩形,
∴∠B
=90°,且AD∥BC.
∴∠1=∠2,
∵DF⊥AE,
∴∠AFD
=
90°.
∴∠B
=∠AFD.又
AD
=
AE
=
BC,
∴△ABE
≌
△DFA(AAS).
∴AF
=
BE.
∴AE-AF
=
BC-BE
∴EF
=
EC.
A
B
C
D
E
F
∠1
∠2
矩形的四个角都是直角.
矩形的两条对角线相等.
直角三角形斜边上的中线等于斜边的一半.
矩形的性质
1
2
矩形性质推论
课堂小结
课后作业
1.从教材习题中选取.
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
