第19章 四边形章末复习 课件(共36张PPT)
文档属性
| 名称 | 第19章 四边形章末复习 课件(共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 20:15:10 | ||
图片预览










文档简介
(共36张PPT)
第19章
四边形
章末复习
沪科版·八年级数学下册
上课课件
学习目标
【知识与技能】
通过对几种平行四边形的回顾与思考,使学生梳理所学的知识,系统地复习平行四边形与各种特殊平行四边形的定义、性质、判定方法;
【过程与方法】
正确理解平行四边形与各种特殊平行四边形的联系与区别,在反思和交流过程中,逐渐建立知识体系;
【情感态度】
引导学生独立思考,通过归纳、概括、实践等系统数学活动,感受获得成功的体验,形成科学的学习习惯.
【教学重点】
1.平行四边形与各种特殊平行四边形的区别.
2.梳理平行四边形、矩形、菱形、正方形的知识体系及应用方法.
【教学难点】
平行四边形与各种特殊平行四边形的定义、性质、判定的综合运用.
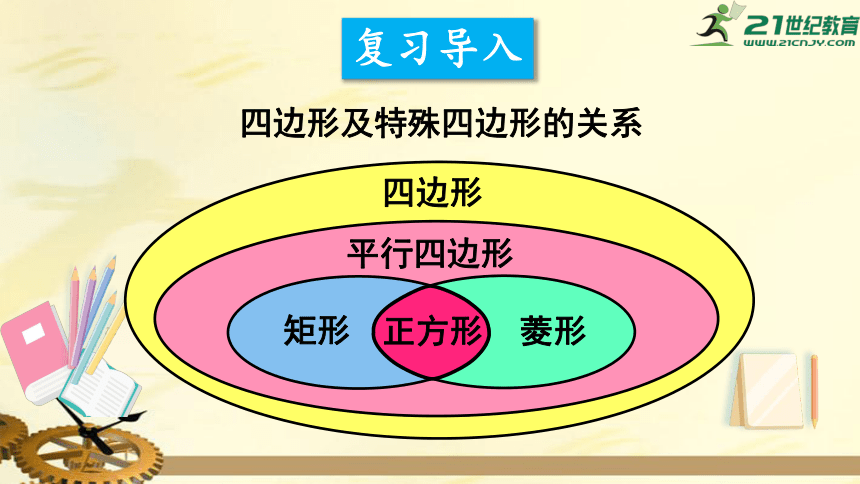
复习导入
四边形及特殊四边形的关系
矩形
菱形
正方形
平行四边形
四边形
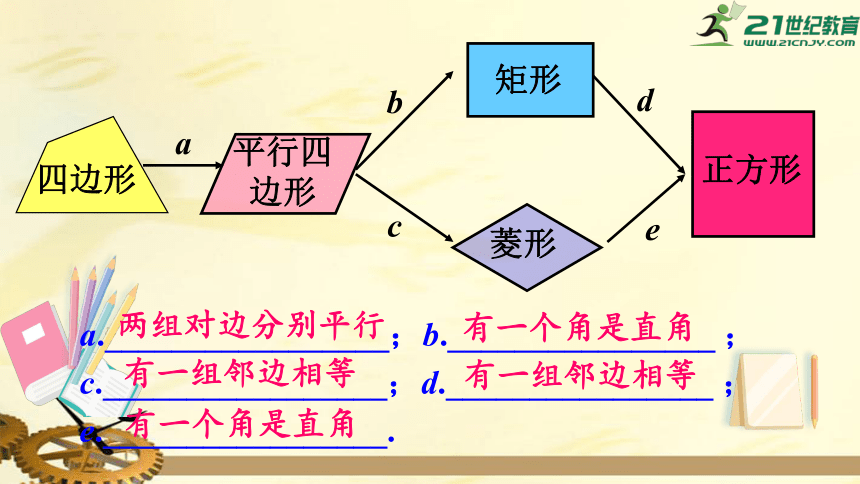
平行四
边形
矩形
菱形
正方形
四边形
a
b
c
d
e
a._________________;b.________________
;
c._________________;d.________________
;
e._________________.
两组对边分别平行
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
平行四边形
定义:________________的四边形是平行四边形.
两组对边分别平行
性质1
平行四边形的对边_____.
相等
性质2
平行四边形的对角_____.
相等
性质3
平行四边形的对角线__________.
互相平分
定理1
一组对边__________的四边形是平行四边形.
定理2
两组对边________的四边形是平行四边形.
定理3
对角线________的四边形是平行四边形.
分别平行
互相平分
平行且相等
判定定理
三角形的中位线
(1)连接三角形两边中点的线段叫做三角形的中位线.
(2)定理:三角形两边中点的连线平行于第三边,并且等于第三边的一半.
①三角形有___条中位线.
②三角形的三条中位线把原三角形分成全等的
4
个小三角形.每个小三角形的周长为原三角形周长的____.每个小三角形的面积为原三角形面积的____.
3
多边形内角和、外角和
(1)n
边形的内角和为___________
(n≥3).
(n-2)·180°
(2)正多边形的每个内角都相等,都等于
_____________.
(n-2)·180°
n
(3)多边形的外角和为360°,它与边数的多少无关.
矩形
定义:_______________的平行四边形是矩形.
有一个角是直角
性质1
矩形的四个角都是直角.
性质2
矩形的两条对角线相等.
推论
直角三角形斜边上的中线等于斜边的一半.
矩形的判定
定理1
对角线相等的平行四边形是矩形.
定理2
三个角是直角的四边形是矩形.
菱形
定义:______________的平行四边形叫做菱形.
有一组邻边相等
性质1
菱形的四条边都_______.
性质2
菱形的对角线_________.
相等
互相垂直
定理1
四条边都相等的四边形是菱形.
定理2
对角线互相垂直的平行四边形是菱形.
菱形的判定
正方形
定义:有一个角是_____,且有一组邻边____的平行四边形叫做正方形.
直角
相等
性质1
正方形的四条边都相等,四个角都是直角.
性质2
正方形的对角线相等且互相垂直平分.
正方形的判定
有一组邻边相等的矩形是正方形.
有一个角为直角的菱形是正方形.
典例解析
例
1
如图,E、F
是平行四边形
ABCD
对角线BD
上的两点,给出下列三个条件:①BE
=
DF;
②∠AEB
=∠DFC;③AF∥
EC.
请你从中选择一个适当的条件____,使四边形
AECF
是平行四边形,并证明你的结论.
①
A
B
C
D
E
F
证明:如图,连接
AC
交
BD
于
O.
∴AO
=
CO,OB
=
OD.
又∵BE
=
DF,∴OB-BE
=
OD-DF,∴OE
=
OF.
又∵AO
=
CO,
∴四边形
AECF
为平行四边形.
A
B
C
D
E
F
o
例
2
如图,点
E、F、G、H
分别为四边形ABCD
的边
AB、BC、CD、DA
的中点,试判断四边形
EFGH
的形状,并证明你的结论.
解:四边形
EFGH
为平行四边形.
如图,连接
AC,在
△ACD
中,H、G
分别为AD、CD
的中点,
∴HG∥AC,HG
=
AC,
同理:EF∥AC,EF
=
AC,
∴HG∥EF,HG
=
EF.
∴四边形
EFGH
为平行四边形.
例
3
如图,四边形
ABCD
是菱形,对角线
AC
=
8
cm,BD
=
6
cm,DH⊥AB
于
H,求高
DH
的长.
解:∵四边形
ABCD
为菱形,
∴AO
=
AC
=
4
cm,AC⊥BD,
∴在
Rt△AOB
中,
(cm).
S△ABD
=
DH
·
AB=
AO
·
BD
∴DH
=
(cm).
例
4
如图,正方形
ABCD
的对角线相交于点O,点
O
是正方形
A′B′C′O
的一个顶点,如果两个正方形的边长相等,那么正方形
A′B′C′O
绕点
O
无论怎样转动,两个正方形重叠部分的面积总等于一个正方形面积的四分之一,你能说明理由吗?
解:∵∠BOF+∠A′OB
=
90°,∠A′OB+∠AOE
=
90°.
∴∠BOF
=∠AOE.
又∵OA
=
OB,∠OAE
=
∠OBF.
∴△AOE
≌
△BOF.
∴S△AOE
=
S△BOF
.
∴S四边形EBFO
=
S△BOF
+
S△OEB
=
S△AOE
+
S
△OEB
=
S正方形ABCD.
例
5
如图,△ABC
中,BD,CE
为高,F
是边
BC
的中点,判断
△DEF
的形状,并说明理由.
解:△DEF
为等腰三角形.
在
Rt△BEC
中,∵F
为
BC
的中点,
∴EF
=
BC.
同理:FD
=
BC.
∴FD
=
EF,
∴
△DEF
为等腰三角形.
例
6
如图,在
△ABC
中,点
O
是
AC
上的一动点,过点
O
作直线
MN∥
BC,设
MN
交∠BCA
的平分线于点
E,交∠BCA
的外角平分线于点
F.
(1)求证:OC
=
EF.
证明:∵CE为∠BCA
的平分线,∴∠BCE
=∠ECO.
又∵MN∥
BC,∠BCE
=∠CEO.
∴∠CEO
=∠ECO,∴EO
=
OC.
同理:OC
=
OF,∴OC
=
EF.
(2)当点
O
运动到何处时,四边形
AECF是矩形?并证明你的结论.
解:当点
O
运动到
AC
的中点时,
四边形
AECF
是矩形.
∵由(1)可知,O
为
EF
的中点,
又∵O
为
AC
的中点.
∴四边形
AECF
为平行四边形.
又∵CE为∠BCA
的平分线,
CF为∠ACD
的平分线,∠ECF
=
90°.
∴四边形
AECF
是矩形.
随堂练习
1.下列图形:矩形、菱形、等腰梯形、正方形中对称轴最多的是(
)
A.
矩形
B.
菱形
C.
等腰梯形
D.
正方形
D
2.
如图,平行四边形
ABCD
中,∠A
的平分线
AE
交
CD
于
E,AB
=
5,BC
=
3,则
EC
的长是(
)
A.
1
B.
2
C.
1.5
D.
3
B
D
A
B
C
E
3.
如图所示,直线
l
过正方形
ABCD
的顶点
B.
A,C
两点到直线
l
的距离分别为
5
和
12,
则正方形的边长是____.
13
4.
如图,在矩形
ABCD
中,AB
=
3,AD
=
4,点
P
在
AD
上,PE⊥AC
于
E,PF⊥BD
于
F,
则
PE
+
PF
=____.
课后作业
1.从教材习题中选取.
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第19章
四边形
章末复习
沪科版·八年级数学下册
上课课件
学习目标
【知识与技能】
通过对几种平行四边形的回顾与思考,使学生梳理所学的知识,系统地复习平行四边形与各种特殊平行四边形的定义、性质、判定方法;
【过程与方法】
正确理解平行四边形与各种特殊平行四边形的联系与区别,在反思和交流过程中,逐渐建立知识体系;
【情感态度】
引导学生独立思考,通过归纳、概括、实践等系统数学活动,感受获得成功的体验,形成科学的学习习惯.
【教学重点】
1.平行四边形与各种特殊平行四边形的区别.
2.梳理平行四边形、矩形、菱形、正方形的知识体系及应用方法.
【教学难点】
平行四边形与各种特殊平行四边形的定义、性质、判定的综合运用.
复习导入
四边形及特殊四边形的关系
矩形
菱形
正方形
平行四边形
四边形
平行四
边形
矩形
菱形
正方形
四边形
a
b
c
d
e
a._________________;b.________________
;
c._________________;d.________________
;
e._________________.
两组对边分别平行
有一个角是直角
有一组邻边相等
有一组邻边相等
有一个角是直角
平行四边形
定义:________________的四边形是平行四边形.
两组对边分别平行
性质1
平行四边形的对边_____.
相等
性质2
平行四边形的对角_____.
相等
性质3
平行四边形的对角线__________.
互相平分
定理1
一组对边__________的四边形是平行四边形.
定理2
两组对边________的四边形是平行四边形.
定理3
对角线________的四边形是平行四边形.
分别平行
互相平分
平行且相等
判定定理
三角形的中位线
(1)连接三角形两边中点的线段叫做三角形的中位线.
(2)定理:三角形两边中点的连线平行于第三边,并且等于第三边的一半.
①三角形有___条中位线.
②三角形的三条中位线把原三角形分成全等的
4
个小三角形.每个小三角形的周长为原三角形周长的____.每个小三角形的面积为原三角形面积的____.
3
多边形内角和、外角和
(1)n
边形的内角和为___________
(n≥3).
(n-2)·180°
(2)正多边形的每个内角都相等,都等于
_____________.
(n-2)·180°
n
(3)多边形的外角和为360°,它与边数的多少无关.
矩形
定义:_______________的平行四边形是矩形.
有一个角是直角
性质1
矩形的四个角都是直角.
性质2
矩形的两条对角线相等.
推论
直角三角形斜边上的中线等于斜边的一半.
矩形的判定
定理1
对角线相等的平行四边形是矩形.
定理2
三个角是直角的四边形是矩形.
菱形
定义:______________的平行四边形叫做菱形.
有一组邻边相等
性质1
菱形的四条边都_______.
性质2
菱形的对角线_________.
相等
互相垂直
定理1
四条边都相等的四边形是菱形.
定理2
对角线互相垂直的平行四边形是菱形.
菱形的判定
正方形
定义:有一个角是_____,且有一组邻边____的平行四边形叫做正方形.
直角
相等
性质1
正方形的四条边都相等,四个角都是直角.
性质2
正方形的对角线相等且互相垂直平分.
正方形的判定
有一组邻边相等的矩形是正方形.
有一个角为直角的菱形是正方形.
典例解析
例
1
如图,E、F
是平行四边形
ABCD
对角线BD
上的两点,给出下列三个条件:①BE
=
DF;
②∠AEB
=∠DFC;③AF∥
EC.
请你从中选择一个适当的条件____,使四边形
AECF
是平行四边形,并证明你的结论.
①
A
B
C
D
E
F
证明:如图,连接
AC
交
BD
于
O.
∴AO
=
CO,OB
=
OD.
又∵BE
=
DF,∴OB-BE
=
OD-DF,∴OE
=
OF.
又∵AO
=
CO,
∴四边形
AECF
为平行四边形.
A
B
C
D
E
F
o
例
2
如图,点
E、F、G、H
分别为四边形ABCD
的边
AB、BC、CD、DA
的中点,试判断四边形
EFGH
的形状,并证明你的结论.
解:四边形
EFGH
为平行四边形.
如图,连接
AC,在
△ACD
中,H、G
分别为AD、CD
的中点,
∴HG∥AC,HG
=
AC,
同理:EF∥AC,EF
=
AC,
∴HG∥EF,HG
=
EF.
∴四边形
EFGH
为平行四边形.
例
3
如图,四边形
ABCD
是菱形,对角线
AC
=
8
cm,BD
=
6
cm,DH⊥AB
于
H,求高
DH
的长.
解:∵四边形
ABCD
为菱形,
∴AO
=
AC
=
4
cm,AC⊥BD,
∴在
Rt△AOB
中,
(cm).
S△ABD
=
DH
·
AB=
AO
·
BD
∴DH
=
(cm).
例
4
如图,正方形
ABCD
的对角线相交于点O,点
O
是正方形
A′B′C′O
的一个顶点,如果两个正方形的边长相等,那么正方形
A′B′C′O
绕点
O
无论怎样转动,两个正方形重叠部分的面积总等于一个正方形面积的四分之一,你能说明理由吗?
解:∵∠BOF+∠A′OB
=
90°,∠A′OB+∠AOE
=
90°.
∴∠BOF
=∠AOE.
又∵OA
=
OB,∠OAE
=
∠OBF.
∴△AOE
≌
△BOF.
∴S△AOE
=
S△BOF
.
∴S四边形EBFO
=
S△BOF
+
S△OEB
=
S△AOE
+
S
△OEB
=
S正方形ABCD.
例
5
如图,△ABC
中,BD,CE
为高,F
是边
BC
的中点,判断
△DEF
的形状,并说明理由.
解:△DEF
为等腰三角形.
在
Rt△BEC
中,∵F
为
BC
的中点,
∴EF
=
BC.
同理:FD
=
BC.
∴FD
=
EF,
∴
△DEF
为等腰三角形.
例
6
如图,在
△ABC
中,点
O
是
AC
上的一动点,过点
O
作直线
MN∥
BC,设
MN
交∠BCA
的平分线于点
E,交∠BCA
的外角平分线于点
F.
(1)求证:OC
=
EF.
证明:∵CE为∠BCA
的平分线,∴∠BCE
=∠ECO.
又∵MN∥
BC,∠BCE
=∠CEO.
∴∠CEO
=∠ECO,∴EO
=
OC.
同理:OC
=
OF,∴OC
=
EF.
(2)当点
O
运动到何处时,四边形
AECF是矩形?并证明你的结论.
解:当点
O
运动到
AC
的中点时,
四边形
AECF
是矩形.
∵由(1)可知,O
为
EF
的中点,
又∵O
为
AC
的中点.
∴四边形
AECF
为平行四边形.
又∵CE为∠BCA
的平分线,
CF为∠ACD
的平分线,∠ECF
=
90°.
∴四边形
AECF
是矩形.
随堂练习
1.下列图形:矩形、菱形、等腰梯形、正方形中对称轴最多的是(
)
A.
矩形
B.
菱形
C.
等腰梯形
D.
正方形
D
2.
如图,平行四边形
ABCD
中,∠A
的平分线
AE
交
CD
于
E,AB
=
5,BC
=
3,则
EC
的长是(
)
A.
1
B.
2
C.
1.5
D.
3
B
D
A
B
C
E
3.
如图所示,直线
l
过正方形
ABCD
的顶点
B.
A,C
两点到直线
l
的距离分别为
5
和
12,
则正方形的边长是____.
13
4.
如图,在矩形
ABCD
中,AB
=
3,AD
=
4,点
P
在
AD
上,PE⊥AC
于
E,PF⊥BD
于
F,
则
PE
+
PF
=____.
课后作业
1.从教材习题中选取.
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
