第三章 变量之间的关系一章一练(含解析)
文档属性
| 名称 | 第三章 变量之间的关系一章一练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 00:00:00 | ||
图片预览




文档简介
初中数学北师大版七年级下学期 第三章 单元测试卷
一、单选题(共8题;每题3分;共24分)
1.下列各曲线中不能表示y是x的函数是(??? )
A.?????????????B.?????????????C.?????????????D.?
2.函数 中,自变量 的取值范围是(?? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
3.如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是(?? )
A.?4℃?????????????????????????????????????B.?8℃?????????????????????????????????????C.?12℃?????????????????????????????????????D.?16℃
4.某人要在规定的时间内加工100个零件,如果用n表示工作效率,用t表示规定的时间,下列说法正确的是(??? )
A.?数100和n,t都是常量????????B.?数100和N都是变量????????C.?n和t都是变量????????D.?数100和t都是变量
5.如图, 中, ,正方形 的顶点 别在 边上,设 的长度为 , 与正方形 重叠部分的面积为 ,则下列图象中能表示 与 之间的函数关系的是(?? )
A.???????????????????B.???????????????????C.???????????????????D.?
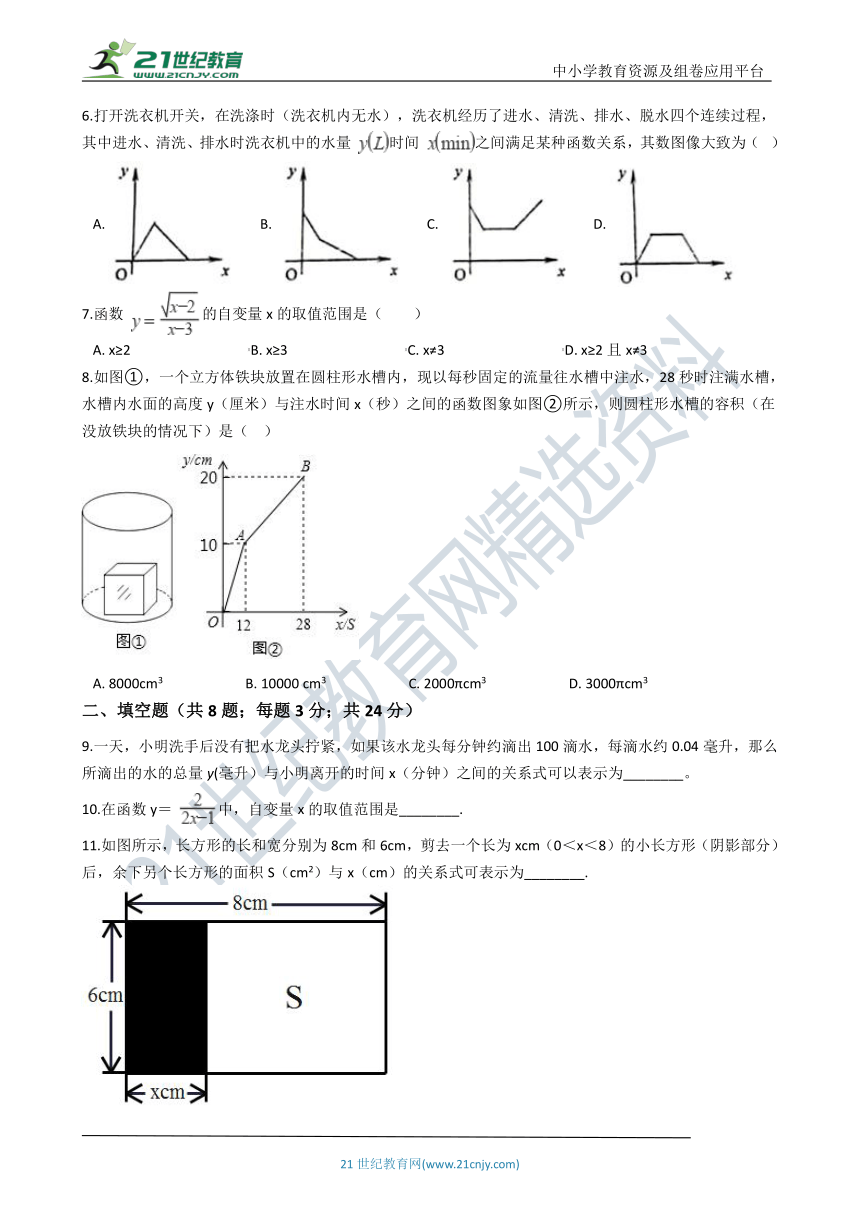
6.打开洗衣机开关,在洗涤时(洗衣机内无水),洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量 时间 之间满足某种函数关系,其数图像大致为(? )
A.?????????B.?????????C.?????????D.?
7.函数 的自变量x的取值范围是( )
A.?x≥2??????????????????????????????????B.?x≥3??????????????????????????????????C.?x≠3??????????????????????????????????D.?x≥2且x≠3
8.如图①,一个立方体铁块放置在圆柱形水槽内,现以每秒固定的流量往水槽中注水,28秒时注满水槽,水槽内水面的高度y(厘米)与注水时间x(秒)之间的函数图象如图②所示,则圆柱形水槽的容积(在没放铁块的情况下)是(?? )
A.?8000cm3????????????????????????B.?10000 cm3????????????????????????C.?2000πcm3????????????????????????D.?3000πcm3
二、填空题(共8题;每题3分;共24分)
9.一天,小明洗手后没有把水龙头拧紧,如果该水龙头每分钟约滴出100滴水,每滴水约0.04毫升,那么所滴出的水的总量y(毫升)与小明离开的时间x(分钟)之间的关系式可以表示为________。
10.在函数y= 中,自变量x的取值范围是________.
11.如图所示,长方形的长和宽分别为8cm和6cm,剪去一个长为xcm(0<x<8)的小长方形(阴影部分)后,余下另个长方形的面积S(cm2)与x(cm)的关系式可表示为________.
12.函数y= 的自变量x的取值范围为________.
13.小明参加了步行活动中,中途休息了一段时间.设他从学校出发后所用时间为 (分钟),所走的路程为 (米 ,s与t之间的函数关系如图17所示.则下列说法中,正确的序号为________.
①小明中途休息用了20分钟.
②小明休息前步行的平均速度为每分钟70米.
③小明休息前步行的平均速度大于休息后步行的平均速度.
④小明行走的路程为6600米.
14.某商城为促进同一款衣服的销量,当同一个人购买件数达到一定数目的时候,超过的件数,每件打8折,现任意挑选5个顾客的消费情况制定表格,其中 表示购买件数, 表示消费金额,根据表格数据请写出一个 关于 的函数解析式是:________.??
(件)
2
3
4
5
6
(元)
100
150
200
240
280
15.函数 的自变量的取值范围是________.
16.某水库的水位在6小时内持续上涨,初始的水位高度为8米,水位以每小时0.2米的速度匀速上升,则水库的水位高度 米与时间 小时( )之间的关系式为________.
三、解答题(共10题;共72分)
17.(5分)写出下列函数关系式,并指出关系式中的自变量和函数: 圆锥的底面半径为定值r,则圆锥的体积V与圆锥的高h之间的关系.
18.(5分)求下列函数中自变量的取值范围.
①y= ②y= .
19.(5分)指出下面各关系式中的常量与变量.
运动员在400m一圈的跑道上训练,他跑一圈所用的时间t(s)与跑步速度v(m/s)之间的函数关系式为t= .
20.(6分)在一次实验中,小明把一根弹簧的端固定,在其下端悬挂物体,下面是测得的弹簧的长度 与所挂物体的质量 的一组对应值:
所挂物体的质量
弹簧长度
(1)在这个变化的过程中,自变量是________;因变量是________;
(2)写出 与 之间的关系式,并求出当所挂重物为 时,弹簧的长度为多少?
21.(8分)为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h)
0
1
2
3
…
油箱剩余油量Q(L)
100
94
88
82
…
(1)在这个变化过程中,________是自变量,________是因变量;(填中文)
(2)根据上表的数据,请你写出Q与t的关系式:________;
(3)汽车行驶6h后,油箱中的剩余油量是________;
(4)该品牌汽车的油箱加满60L , 若以100km/h的速度匀速行驶,该车最多能行驶________km .
22.(9分)某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
(1)学校离他家多远?从出发到学校,用了多少时间?
(2)王老师吃早餐用了多少时间?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?
23.(9分)如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲乙所行驶的路程S和时间t的关系.
根据图象回答下列问题:
(1)甲和乙哪一个出发的更早?早出发多长时间?
(2)甲和乙哪一个早到达B城?早多长时间?
(3)乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少?
(4)请你根据图象上的数据,求出乙出发用多长时间就追上甲?
24.(9分)甲、乙两山地自行车选手进行骑行训练.他们在同地出发,反向而行,分别前往A地和B地.甲先出发一分钟且先到达A地.两人到达目的地后均以原速按原路立即返回,直至两人相遇.下图是两人之间的距离y(千米)随乙出发时间x(分钟)之间的变化图象.请根据图象解决下列问题:
(1)直接写出甲车和乙车的速度.
(2)在图中的两个括号内填上正确的数值.
(3)乙车出发多长时间两车首次相距22.6千米?
25.(8分)一个周末上午8:00,小张自驾小汽车从家出发,带全家人去一个4A级景区游玩,小张驾驶的小汽车离家的距离 (千米)与时间 (时)之间的关系如图所示,请结合图象解决下列问题:
(1)小张家距离景区________千米,全家人在景区游玩了________小时;
(2)在去景区的路上,汽车进行了一次加油,之后平均速度比原来增加了20千米 时,试求他加油共用了多少小时?
(3)如果汽车油箱中原来有油25升,平均每小时耗油10升,问小张在加油站至少加多少油才能开回家?
26.(8分)现代营养学家用体重指数判断人体的健康状况,这个指数等于人体质量(千克)与人体身高(米)的平方的商,一个健康人的体重指数在18.5?26.9之间,体重指数低于18.5,属于不健康的消瘦;体重指数高于26.9,属于不健康的肥胖.
(1)A同志的体重为90千克,身高为1.6米,A同志的健康状况如何?
(2)B同志的体重在65?70千克之间,经测定该同志的体重指数为23,请估算B同志的身高.
答案解析部分
一、单选题
1.【答案】 B
解:根据题图可知,A、C、D三选项中,对于自变量x的任何值,y都有唯一的值与之相对应,y是x的函数;
B、对于 的任何值,y都有二个值与之相对应,则y不是x的函数;
故答案为:B.
2.【答案】 C
解:根据题意得,2x?5≥0,
解得 .
故答案为:C.
3.【答案】 C
解:从折线统计图中可以看出,这一天中最高气温8℃,最低气温是﹣4℃,这一天中最高气温与最低气温的差为12℃,
故答案为:C.
4.【答案】 C
解:数100是常量,t,n是变量,故ABD不符合题意,C符合题意.
故答案为:C.
5.【答案】 A
解:当0<x≤1时,
?当1<x≤2时,ED交AB于M,EF交AB于N,
如图, CD=x,则AD=2-x,
∵Rt△ABC中,AC=BC=2,
?∴△ADM为等腰直角三角形,
?∴DM=2-x,
?∴EM=x-(2-x)=2x-2,
?∴
?∴
∴
故答案为:A.
6.【答案】 D
解:因为进水时水量增加,函数图象的走势向上,所以可以排除B、C,清洗时水量大致不变,函数图象与x轴平行,排水时水量减少,函数图象的走势向下,排除A,只有选项D符合.
故答案为:D.
7.【答案】 D
解:根据题意得:x﹣2≥0且x﹣3≠0,
解得:x≥2且x≠3.
故答案为:D.
8.【答案】 A
解:由题意可得:12秒时,水槽内水面的高度为10cm,12秒后水槽内高度变化趋势改变,
∴正方体的棱长为10cm;
∴正方体的体积为:103=1000cm3
设注水的速度为xcm3/s,圆柱的底面积为scm2 , 根据题意得:
解得:
∴圆柱形水槽的容积为:400×20=8000 cm3.
故答案为:A.
二、填空题
9.【答案】 y=4x
解:由题意得:y=0.04×100x=4x,
故答案为:y=4x.
10.【答案】 x≠
解:由题意,得
2x﹣1≠0,
解得x≠ ,
故答案为:x≠ .
11.【答案】 S=-6x+48
解:∵长方形的长和宽分别为8cm和6cm,剪去一个长为xcm(0<x<8)的小长方形(阴影部分)后,
∴余下另一个长方形的面积S(cm2)与x(cm)的关系式可表示为:S=6(8-x).即S=-6x+48.
故答案是:S=-6x+48.
12.【答案】x≥﹣1且x≠0
解:∵x+1≥0,且 ﹣1≠0, ∴x≥﹣1且x≠0,
故答案为x≥﹣1且x≠0.
13.【答案】 ①②③
解:①由图象可知,在40~60分钟,路程没有发生变化,
∴小明中途休息的时间为60-40=20(分钟),故①正确;
②由图象知:当t=40时,s=2800,
∴ 小明休息前步行的平均速度为2800÷40=70(米/分),故B正确;
③ 休息后步行的平均速度为:(3800-2800)÷(100-60)=25(米/分),
由②知小明休息前步行的平均速度为70米/分,
∵70>25,∴小明休息前步行的平均速度大于休息后步行的平均速度,故③正确;
④根据图形可知, 小明行走的路程为3800米,故④错误;
∴正确有①②③.
14.【答案】
解:由题意可得:当超过一定件数时,超过的件数打8折,
当x=2时,y=100;当x=3时,y=150;当x=4时,y=200,
可知:该件衣服的单价为50元一件,
由表中数据可得:当超过4件时,超过的部分打8折,
∴当x≤4时,y=50x,
当x>4时,y=4×50+(x-4)×0.8×50=40x+40,
∴y与x的表达式为: ,
故答案为: .
15.【答案】
解:由题意得,2x-1≥0且x+3≠0,
解得:x≥ ,
故答案为:x≥ .
16.【答案】 y=0.2x+8
解:根据题意可得:y=8+0.2x(0?x?6),
故答案为:y=8+0.2x.
三、解答题
17.【答案】解:圆锥的体积公式为:V= πr2h, ∴圆锥的体积V与圆锥的高h之间的函数关系式为:V= πr2h,
函数自变量为h,V为自变量h的函数
18.【答案】 解:①根据题意得,2x﹣1≠0,
解得x≠ ;
②根据题意得,2x﹣1≥0,
解得x≥
19.【答案】 解:运动员在400m一圈的跑道上训练,他跑一圈所用的时间t(s)与跑步速度v(m/s)之间的函数关系式为t= ,
常量是400m,变量是v、t
20.【答案】 解:(1)所挂物体的质量;弹簧的长度
(2)由表格可得:当所挂物体重量为1千克时,弹簧长20厘米;当不挂重物时,弹簧长18厘米,物体每增加1kg,弹簧伸长2cm
∴y=2x+18;
当所挂重物为6kg时,弹簧的长度为:y=12+18=30(cm).
21.【答案】 (1)汽车行驶时间;油箱剩余油量
(2)Q=100-6t
(3)64L
(4)解:贮满60L汽油的汽车,最多能行驶t= (小时), ∴10×100=1000(km), 该车最多能行驶1000km;
解:(1)在这个变化过程中,汽车行驶时间是自变量,油箱剩余油量是因变量;(2)由题意可知,Q=100-6t;(3)当t=6时,Q=100-6×6=64;
即汽车行驶6h后,油箱中的剩余油量是64L;
22.【答案】 (1)解:依题意得:学校离王老师家有10千米,从出发到学校王老师用了25分钟
(2)解:依题意得:王老师吃早餐用了10分钟
(3)解:吃早餐以前的速度为:5÷10=0.5km/分钟,吃完早餐以后的速度为:(10﹣5)÷(25﹣20)=1km/分钟=60km/小时,
∴王老师吃完早餐以后速度快,最快时速达到60km/小时
23.【答案】 (1)解:甲下午1时出发,乙下午2时出发,
所以甲更早,早出发1小时
(2)解:甲5时到达,乙3时到达,
所以乙更早,早到2小时
(3)解:乙的速度= =50(千米/小时),
甲的平均速度= =12.5(千米/小时)
(4)解:设乙出发x小时就追上甲,
根据题意得:50x=20+10x,
x=0.5,
答:乙出发0.5小时就追上甲
24.【答案】 (1)36千米/小时,30千米/小时
(2)33|66
(3)解:设乙车出发x时间两车首次相距22.6千米,
根据题意得:
解得: ,
所以乙车出发20分钟后两车首次相距22.6千米.
解:(1)甲的速度是: 千米/小时;
乙的速度是: 千米/分钟 千米/小时;(2)根据题意得:6×(0.6-0.5)=0.6千米,
33.6-0.6=33千米;
33÷(0.6+0.5)=30分钟,
36+30=66分钟;
25.【答案】 (1)200;4.5
(2)解:120÷(9.5?8)=80(千米/时),
200?12080+20=0.8(小时),
10.5?9.5?0.8=0.2(小时),
故他加油共用了0.2小时;
(3)解:200÷200?12016?15=2.5(小时),
9.5?8+0.8+2.5=4.8(小时),
10×4.8?25=23(升),
故小张在加油站至少加23升油才能开回家.
解:(1)由图示信息可知,小张家距离景区200千米,在景区停留了15?10.5=4.5(小时),所以游玩了4.5小时,
故答案为:200;4.5;
26.【答案】 (1)解:A同志的指数= =35.16,身体质量指数高于26.9,所以A同志属于不健康的胖;
(2)解:B同志的指数= =23,身高2= ,又∵B同志的体重在65~70之间,
如果体重为65千克,则身高= =1.68(米);如果体重为70千克,则身高= =1.74(米),∴B同志的身高在1.68至1.74之间.
一、单选题(共8题;每题3分;共24分)
1.下列各曲线中不能表示y是x的函数是(??? )
A.?????????????B.?????????????C.?????????????D.?
2.函数 中,自变量 的取值范围是(?? )
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
3.如图,是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是(?? )
A.?4℃?????????????????????????????????????B.?8℃?????????????????????????????????????C.?12℃?????????????????????????????????????D.?16℃
4.某人要在规定的时间内加工100个零件,如果用n表示工作效率,用t表示规定的时间,下列说法正确的是(??? )
A.?数100和n,t都是常量????????B.?数100和N都是变量????????C.?n和t都是变量????????D.?数100和t都是变量
5.如图, 中, ,正方形 的顶点 别在 边上,设 的长度为 , 与正方形 重叠部分的面积为 ,则下列图象中能表示 与 之间的函数关系的是(?? )
A.???????????????????B.???????????????????C.???????????????????D.?
6.打开洗衣机开关,在洗涤时(洗衣机内无水),洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量 时间 之间满足某种函数关系,其数图像大致为(? )
A.?????????B.?????????C.?????????D.?
7.函数 的自变量x的取值范围是( )
A.?x≥2??????????????????????????????????B.?x≥3??????????????????????????????????C.?x≠3??????????????????????????????????D.?x≥2且x≠3
8.如图①,一个立方体铁块放置在圆柱形水槽内,现以每秒固定的流量往水槽中注水,28秒时注满水槽,水槽内水面的高度y(厘米)与注水时间x(秒)之间的函数图象如图②所示,则圆柱形水槽的容积(在没放铁块的情况下)是(?? )
A.?8000cm3????????????????????????B.?10000 cm3????????????????????????C.?2000πcm3????????????????????????D.?3000πcm3
二、填空题(共8题;每题3分;共24分)
9.一天,小明洗手后没有把水龙头拧紧,如果该水龙头每分钟约滴出100滴水,每滴水约0.04毫升,那么所滴出的水的总量y(毫升)与小明离开的时间x(分钟)之间的关系式可以表示为________。
10.在函数y= 中,自变量x的取值范围是________.
11.如图所示,长方形的长和宽分别为8cm和6cm,剪去一个长为xcm(0<x<8)的小长方形(阴影部分)后,余下另个长方形的面积S(cm2)与x(cm)的关系式可表示为________.
12.函数y= 的自变量x的取值范围为________.
13.小明参加了步行活动中,中途休息了一段时间.设他从学校出发后所用时间为 (分钟),所走的路程为 (米 ,s与t之间的函数关系如图17所示.则下列说法中,正确的序号为________.
①小明中途休息用了20分钟.
②小明休息前步行的平均速度为每分钟70米.
③小明休息前步行的平均速度大于休息后步行的平均速度.
④小明行走的路程为6600米.
14.某商城为促进同一款衣服的销量,当同一个人购买件数达到一定数目的时候,超过的件数,每件打8折,现任意挑选5个顾客的消费情况制定表格,其中 表示购买件数, 表示消费金额,根据表格数据请写出一个 关于 的函数解析式是:________.??
(件)
2
3
4
5
6
(元)
100
150
200
240
280
15.函数 的自变量的取值范围是________.
16.某水库的水位在6小时内持续上涨,初始的水位高度为8米,水位以每小时0.2米的速度匀速上升,则水库的水位高度 米与时间 小时( )之间的关系式为________.
三、解答题(共10题;共72分)
17.(5分)写出下列函数关系式,并指出关系式中的自变量和函数: 圆锥的底面半径为定值r,则圆锥的体积V与圆锥的高h之间的关系.
18.(5分)求下列函数中自变量的取值范围.
①y= ②y= .
19.(5分)指出下面各关系式中的常量与变量.
运动员在400m一圈的跑道上训练,他跑一圈所用的时间t(s)与跑步速度v(m/s)之间的函数关系式为t= .
20.(6分)在一次实验中,小明把一根弹簧的端固定,在其下端悬挂物体,下面是测得的弹簧的长度 与所挂物体的质量 的一组对应值:
所挂物体的质量
弹簧长度
(1)在这个变化的过程中,自变量是________;因变量是________;
(2)写出 与 之间的关系式,并求出当所挂重物为 时,弹簧的长度为多少?
21.(8分)为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h)
0
1
2
3
…
油箱剩余油量Q(L)
100
94
88
82
…
(1)在这个变化过程中,________是自变量,________是因变量;(填中文)
(2)根据上表的数据,请你写出Q与t的关系式:________;
(3)汽车行驶6h后,油箱中的剩余油量是________;
(4)该品牌汽车的油箱加满60L , 若以100km/h的速度匀速行驶,该车最多能行驶________km .
22.(9分)某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
(1)学校离他家多远?从出发到学校,用了多少时间?
(2)王老师吃早餐用了多少时间?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?
23.(9分)如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲乙所行驶的路程S和时间t的关系.
根据图象回答下列问题:
(1)甲和乙哪一个出发的更早?早出发多长时间?
(2)甲和乙哪一个早到达B城?早多长时间?
(3)乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少?
(4)请你根据图象上的数据,求出乙出发用多长时间就追上甲?
24.(9分)甲、乙两山地自行车选手进行骑行训练.他们在同地出发,反向而行,分别前往A地和B地.甲先出发一分钟且先到达A地.两人到达目的地后均以原速按原路立即返回,直至两人相遇.下图是两人之间的距离y(千米)随乙出发时间x(分钟)之间的变化图象.请根据图象解决下列问题:
(1)直接写出甲车和乙车的速度.
(2)在图中的两个括号内填上正确的数值.
(3)乙车出发多长时间两车首次相距22.6千米?
25.(8分)一个周末上午8:00,小张自驾小汽车从家出发,带全家人去一个4A级景区游玩,小张驾驶的小汽车离家的距离 (千米)与时间 (时)之间的关系如图所示,请结合图象解决下列问题:
(1)小张家距离景区________千米,全家人在景区游玩了________小时;
(2)在去景区的路上,汽车进行了一次加油,之后平均速度比原来增加了20千米 时,试求他加油共用了多少小时?
(3)如果汽车油箱中原来有油25升,平均每小时耗油10升,问小张在加油站至少加多少油才能开回家?
26.(8分)现代营养学家用体重指数判断人体的健康状况,这个指数等于人体质量(千克)与人体身高(米)的平方的商,一个健康人的体重指数在18.5?26.9之间,体重指数低于18.5,属于不健康的消瘦;体重指数高于26.9,属于不健康的肥胖.
(1)A同志的体重为90千克,身高为1.6米,A同志的健康状况如何?
(2)B同志的体重在65?70千克之间,经测定该同志的体重指数为23,请估算B同志的身高.
答案解析部分
一、单选题
1.【答案】 B
解:根据题图可知,A、C、D三选项中,对于自变量x的任何值,y都有唯一的值与之相对应,y是x的函数;
B、对于 的任何值,y都有二个值与之相对应,则y不是x的函数;
故答案为:B.
2.【答案】 C
解:根据题意得,2x?5≥0,
解得 .
故答案为:C.
3.【答案】 C
解:从折线统计图中可以看出,这一天中最高气温8℃,最低气温是﹣4℃,这一天中最高气温与最低气温的差为12℃,
故答案为:C.
4.【答案】 C
解:数100是常量,t,n是变量,故ABD不符合题意,C符合题意.
故答案为:C.
5.【答案】 A
解:当0<x≤1时,
?当1<x≤2时,ED交AB于M,EF交AB于N,
如图, CD=x,则AD=2-x,
∵Rt△ABC中,AC=BC=2,
?∴△ADM为等腰直角三角形,
?∴DM=2-x,
?∴EM=x-(2-x)=2x-2,
?∴
?∴
∴
故答案为:A.
6.【答案】 D
解:因为进水时水量增加,函数图象的走势向上,所以可以排除B、C,清洗时水量大致不变,函数图象与x轴平行,排水时水量减少,函数图象的走势向下,排除A,只有选项D符合.
故答案为:D.
7.【答案】 D
解:根据题意得:x﹣2≥0且x﹣3≠0,
解得:x≥2且x≠3.
故答案为:D.
8.【答案】 A
解:由题意可得:12秒时,水槽内水面的高度为10cm,12秒后水槽内高度变化趋势改变,
∴正方体的棱长为10cm;
∴正方体的体积为:103=1000cm3
设注水的速度为xcm3/s,圆柱的底面积为scm2 , 根据题意得:
解得:
∴圆柱形水槽的容积为:400×20=8000 cm3.
故答案为:A.
二、填空题
9.【答案】 y=4x
解:由题意得:y=0.04×100x=4x,
故答案为:y=4x.
10.【答案】 x≠
解:由题意,得
2x﹣1≠0,
解得x≠ ,
故答案为:x≠ .
11.【答案】 S=-6x+48
解:∵长方形的长和宽分别为8cm和6cm,剪去一个长为xcm(0<x<8)的小长方形(阴影部分)后,
∴余下另一个长方形的面积S(cm2)与x(cm)的关系式可表示为:S=6(8-x).即S=-6x+48.
故答案是:S=-6x+48.
12.【答案】x≥﹣1且x≠0
解:∵x+1≥0,且 ﹣1≠0, ∴x≥﹣1且x≠0,
故答案为x≥﹣1且x≠0.
13.【答案】 ①②③
解:①由图象可知,在40~60分钟,路程没有发生变化,
∴小明中途休息的时间为60-40=20(分钟),故①正确;
②由图象知:当t=40时,s=2800,
∴ 小明休息前步行的平均速度为2800÷40=70(米/分),故B正确;
③ 休息后步行的平均速度为:(3800-2800)÷(100-60)=25(米/分),
由②知小明休息前步行的平均速度为70米/分,
∵70>25,∴小明休息前步行的平均速度大于休息后步行的平均速度,故③正确;
④根据图形可知, 小明行走的路程为3800米,故④错误;
∴正确有①②③.
14.【答案】
解:由题意可得:当超过一定件数时,超过的件数打8折,
当x=2时,y=100;当x=3时,y=150;当x=4时,y=200,
可知:该件衣服的单价为50元一件,
由表中数据可得:当超过4件时,超过的部分打8折,
∴当x≤4时,y=50x,
当x>4时,y=4×50+(x-4)×0.8×50=40x+40,
∴y与x的表达式为: ,
故答案为: .
15.【答案】
解:由题意得,2x-1≥0且x+3≠0,
解得:x≥ ,
故答案为:x≥ .
16.【答案】 y=0.2x+8
解:根据题意可得:y=8+0.2x(0?x?6),
故答案为:y=8+0.2x.
三、解答题
17.【答案】解:圆锥的体积公式为:V= πr2h, ∴圆锥的体积V与圆锥的高h之间的函数关系式为:V= πr2h,
函数自变量为h,V为自变量h的函数
18.【答案】 解:①根据题意得,2x﹣1≠0,
解得x≠ ;
②根据题意得,2x﹣1≥0,
解得x≥
19.【答案】 解:运动员在400m一圈的跑道上训练,他跑一圈所用的时间t(s)与跑步速度v(m/s)之间的函数关系式为t= ,
常量是400m,变量是v、t
20.【答案】 解:(1)所挂物体的质量;弹簧的长度
(2)由表格可得:当所挂物体重量为1千克时,弹簧长20厘米;当不挂重物时,弹簧长18厘米,物体每增加1kg,弹簧伸长2cm
∴y=2x+18;
当所挂重物为6kg时,弹簧的长度为:y=12+18=30(cm).
21.【答案】 (1)汽车行驶时间;油箱剩余油量
(2)Q=100-6t
(3)64L
(4)解:贮满60L汽油的汽车,最多能行驶t= (小时), ∴10×100=1000(km), 该车最多能行驶1000km;
解:(1)在这个变化过程中,汽车行驶时间是自变量,油箱剩余油量是因变量;(2)由题意可知,Q=100-6t;(3)当t=6时,Q=100-6×6=64;
即汽车行驶6h后,油箱中的剩余油量是64L;
22.【答案】 (1)解:依题意得:学校离王老师家有10千米,从出发到学校王老师用了25分钟
(2)解:依题意得:王老师吃早餐用了10分钟
(3)解:吃早餐以前的速度为:5÷10=0.5km/分钟,吃完早餐以后的速度为:(10﹣5)÷(25﹣20)=1km/分钟=60km/小时,
∴王老师吃完早餐以后速度快,最快时速达到60km/小时
23.【答案】 (1)解:甲下午1时出发,乙下午2时出发,
所以甲更早,早出发1小时
(2)解:甲5时到达,乙3时到达,
所以乙更早,早到2小时
(3)解:乙的速度= =50(千米/小时),
甲的平均速度= =12.5(千米/小时)
(4)解:设乙出发x小时就追上甲,
根据题意得:50x=20+10x,
x=0.5,
答:乙出发0.5小时就追上甲
24.【答案】 (1)36千米/小时,30千米/小时
(2)33|66
(3)解:设乙车出发x时间两车首次相距22.6千米,
根据题意得:
解得: ,
所以乙车出发20分钟后两车首次相距22.6千米.
解:(1)甲的速度是: 千米/小时;
乙的速度是: 千米/分钟 千米/小时;(2)根据题意得:6×(0.6-0.5)=0.6千米,
33.6-0.6=33千米;
33÷(0.6+0.5)=30分钟,
36+30=66分钟;
25.【答案】 (1)200;4.5
(2)解:120÷(9.5?8)=80(千米/时),
200?12080+20=0.8(小时),
10.5?9.5?0.8=0.2(小时),
故他加油共用了0.2小时;
(3)解:200÷200?12016?15=2.5(小时),
9.5?8+0.8+2.5=4.8(小时),
10×4.8?25=23(升),
故小张在加油站至少加23升油才能开回家.
解:(1)由图示信息可知,小张家距离景区200千米,在景区停留了15?10.5=4.5(小时),所以游玩了4.5小时,
故答案为:200;4.5;
26.【答案】 (1)解:A同志的指数= =35.16,身体质量指数高于26.9,所以A同志属于不健康的胖;
(2)解:B同志的指数= =23,身高2= ,又∵B同志的体重在65~70之间,
如果体重为65千克,则身高= =1.68(米);如果体重为70千克,则身高= =1.74(米),∴B同志的身高在1.68至1.74之间.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
