2020-2021学年度高中数学单元双基精品试卷 选修1-2第一章统计案例(A)(含答案)
文档属性
| 名称 | 2020-2021学年度高中数学单元双基精品试卷 选修1-2第一章统计案例(A)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 00:00:00 | ||
图片预览




文档简介
-1123950339725此卷只装订不密封
班级 姓名 准考证号 考场号 座位号
此卷只装订不密封
班级 姓名 准考证号 考场号 座位号
2020-2021学年度高中数学单元双基精品试卷
选修1-2第一章统计案例 (A)
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列关于回归分析与独立性检验的说法正确的是( )
①回归分析和独立性检验没有什么区别;
②回归分析是对两个变量准确关系的分析,而独立性检验是分析两个变量之间的不确定性关系;
③回归分析研究两个变量之间的相关关系,独立性检验是对两个变量是否具有某种关系的一种检验;
④独立性检验可以确定两个变量之间是否具有某种关系.
A.①② B.③ C.③④ D.全选
2.“人机大战,柯洁哭了,机器赢了”,2017年5月27日,19岁的世界围棋第一人柯洁不敌人工智能系统AlphaGo,落泪离席.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查.在参与调查的2600男性中,有1560人持反对意见,2400名女性中,有1118人持反对意见.再运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是( )
A.分层抽样 B.回归分析
C.独立性检验 D.频率分布直方图
3.为了研究某大型超市开业天数与销售额的情况,随机抽取了5天,其开业天数与每天的销售额的情况如表所示:
开业天数
10
20
30
40
50
销售额/天(万元)
62
75
81
89
根据上表提供的数据,求得关于的线性回归方程为,由于表中有一个数据模糊看不清,请你推断出该数据的值为( )
A. B. C. D.
4.某村庄对该村内名老年人、年轻人每年是否体检的情况进行了调查,统计数据如表所示:
每年体检
每年未体检
合计
老年人
年轻人
合计
已知抽取的老年人、年轻人各名,则对列联表数据的分析错误的是( )
A. B. C. D.
5.对四组数据进行统计,获得以下散点图,关于其线性相关系数比较,正确的是( )
A. B.
C. D.
6.下列说法错误的是( )
A.自变量取值一定时,因变量的取值有一定随机性的两个变量之间的关系叫做相关关系
B.在线性回归分析中,相关系数越大,变量间的相关性越强
C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D.在回归分析中,为的模型比为的模型拟合的效果好
7.下图是相关变量的散点图,现对这两个变量进行线性相关分析,方案一:根据图中所有数据,得到线性回归方程,相关系数为;方案二:剔除点,根据剩下数据,得到线性回归方程,相关系数为,则( )
A. B.
C. D.
8.某种产品的广告费支出与销售额(单位:万元)之间有如表关系,与的线性回归方程为,当广告支出5万元时,随机误差的效应(残差)为( )
2
4
5
6
8
30
40
60
50
70
A.10 B.20 C.30 D.40
9.某商场为了了解毛衣的月销售量(件)与月平均气温()之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温
17
13
8
2
月销售量(件)
24
33
40
55
由表中数据算出线性回归方程中的,气象部门预测下个月的平均气温为,据此估计该商场下个月毛衣销售量约为( )
A.58件 B.40件 C.38件 D.46件
10.2020年初,新型冠状病毒(COVID-19)引起的肺炎疫情爆发以来,各地医疗机构采取了各种针对性的治疗方法,取得了不错的成效,某地开始使用中西医结合方法后,每周治愈的患者人数如下表所示:
周数(x)
1
2
3
4
5
治愈人数(y)
2
17
36
93
142
由表格可得y关于x的二次回归方程为,则此回归模型第2周的残差(实际值与预报值之差)为( )
A.5 B.4 C.1 D.0
11.假设有两个分类变量和的列联表为:
????????
总计
总计
对同一样本,以下数据能说明与有关系的可能性最大的一组为( )
参考公式:,其中.
A. B.
C. D.
12.以模型去拟合一组数据时,为了求出回归方程,设,其变换后得到线性回归方程,则( )
A. B. C. D.
二、填空题:本大题共4小题,每小题5分.
13.下列说法中,正确的有_______.
①回归直线恒过点,且至少过一个样本点;
②根据列列联表中的数据计算得出,而,则有99%的把握认为两个分类变量有关系;
③是用来判断两个分类变量是否相关的随机变量,当的值很小时可以推断两个变量不相关.
14.甲?乙?丙?丁四位同学各自对A,B两个变量的线性相关性做试验,并用回归分析方法分别求得相关系数r与残差平方和m,如下表:
甲
乙
丙
丁
则________同学的试验结果体现A,B两变量有更强的线性相关性.
15.为了研究某种细菌在特定环境下,随时间变化繁殖情况,得如下实验数据,计算得回归方程为.由以上信息,得到下表中c的值为_________.
天数t(天)
繁殖个数y(千个)
16.有两个分类变量和,其中一组观测值为如下的2×2列联表:
总计
15
50
总计
20
45
65
其中,均为大于5的整数,则__________时,在犯错误的概率不超过的前提下为“和之间有关系”.附:.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
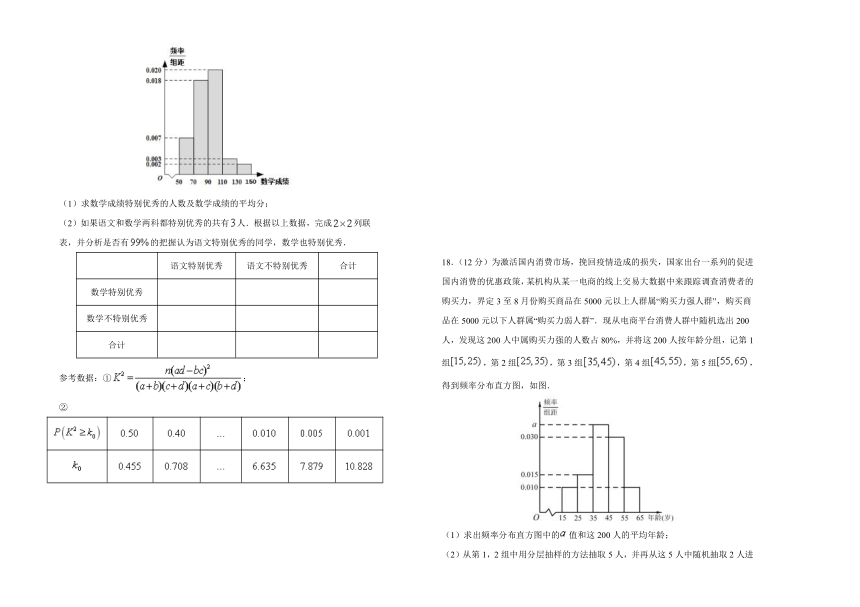
17.(10分)在一次模拟考试中,某校共有名文科学生参加考试,其中语文考试成绩低于的占,如果成绩不低于的为特别优秀,数学成绩的频率分布直方图如图.
(1)求数学成绩特别优秀的人数及数学成绩的平均分;
(2)如果语文和数学两科都特别优秀的共有人.根据以上数据,完成列联表,并分析是否有的把握认为语文特别优秀的同学,数学也特别优秀.
语文特别优秀
语文不特别优秀
合计
数学特别优秀
数学不特别优秀
合计
参考数据:①;
②
…
…
18.(12分)为激活国内消费市场,挽回疫情造成的损失,国家出台一系列的促进国内消费的优惠政策,某机构从某一电商的线上交易大数据中来跟踪调查消费者的购买力,界定3至8月份购买商品在5000元以上人群属“购买力强人群”,购买商品在5000元以下人群属“购买力弱人群”.现从电商平台消费人群中随机选出200人,发现这200人中属购买力强的人数占80%,并将这200人按年龄分组,记第1组,第2组,第3组,第4组,第5组,得到频率分布直方图,如图.
(1)求出频率分布直方图中的值和这200人的平均年龄;
(2)从第1,2组中用分层抽样的方法抽取5人,并再从这5人中随机抽取2人进行电话回访,求这两人恰好属于不同组别的概率;
(3)把年龄在第1,2,3组的居民称为青少年组,年龄在第4,5组的居民称为中老年组,若选出的200人中“购买力弱人群”的中老年人有20人,问是否有99%的把握认为是否属“购买力强人群”与年龄有关?
附:
,.
19.(12分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗(吨标准煤)的几组对应数据.
3
4
5
6
7
3
3
4
5
5
(1)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;
(2)已知该厂技改前,100吨甲产品的生产能耗为70吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低了多少吨标准煤?
参考公式,.
20.(12分)我国探月工程嫦娥五号探测器于2020年12月1日23时11分降落在月球表面预选着陆区,在顺利完成月面自动采样之后,成功将携带样品的上升器送入到预定环月轨道,这是我国首次实现月球无人采样和地外天体起飞,对我国航天事业具有重大而深远的影响,为进一步培养中学生对航空航天的兴趣爱好,某学校航空航天社团在本校高一年级进行了纳新工作,前五天的报名情况为:第1天3人,第2天6人,第3天10人,第4天13人,第5天18人,通过数据分析已知,报名人数与报名时间具有线性相关关系.
(1)已知第天的报名人数为,求关于的线性回归方程,并预测第7天的报名人数(结果四舍五入取整数);
(2)该社团为了解中学生对航空航天的兴趣爱好和性别是否有关系,随机调查了100名学生,并得到如下列联表:
有兴趣
无兴趣
合计
男生
45
5
50
女生
30
20
50
合计
75
25
100
请根据上面的列联表判断能否在犯错误的概率不超过的条件下认为“中学生对航空航天的兴趣爱好和性别有关系”.
参考公式及数据:回归方程中斜率的最小二乘估计公式为:,;
,其中.
21.(12分)某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每批产品的非原料总成本(元)与生产该产品的数量(千件)有关,经统计得到如下数据:
1
2
3
4
5
6
7
6
11
21
34
66
101
196
根据以上数据,绘制如图所示的散点图.
观察散点图,两个变量不具有线性相关关系,现考虑用对数函数模型和指数函数模型分别对两个变量的关系进行拟合.
(1)根据散点图判断,与(,均为大于零的常数)哪一个适宜作为非原料总成本关于生产该产品的数量的回归方程类型;(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表1中的数据,建立关于的回归方程;
(3)已知每件产品的原料成本为10元,若该产品的总成本不得高于123470元,请估计最多能生产多少千件产品.
参考数据:
其中,.
参考公式:对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计公式分别为,.
22.(12分)我国为全面建设社会主义现代化国家,制定了从2021年到2025年的“十四五”规划.某企业为响应国家号召,汇聚科研力量,加强科技创新,准备增加研发资金.现该企业为了了解年研发资金投入额(单位:亿元)对年盈利额(单位:亿元)的影响,研究了“十二五”和“十三五”规划发展期间近10年年研发资金投入额和年盈利额的数据.通过对比分析,建立了两个函数模型:①,②,其中,,,均为常数,为自然对数的底数.
令,,经计算得如下数据:
(1)请从相关系数的角度,分析哪一个模型拟合程度更好?
(2)(ⅰ)根据(1)的选择及表中数据,建立关于的回归方程;(系数精确到)
(ⅱ)若希望2021年盈利额为250亿元,请预测2021年的研发资金投入额为多少亿元?(结果精确到)
附:①相关系数,回归直线中:,.
②参考数据:,.
统计案例(A)答 案
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】B
【解析】回归分析是对两个变量之间的相关关系的一种分析,而相关关系是一种不确定关系,通过回归分析可能两个变量之间具有的相关关系.
而独立性检验是对两个变量之间是否具有某种关系的分析,并且可以分析这两个变量在多大程度上具有这种关系,但不能100%肯定这种关系,
故①②④错误,③正确,故选B.
2.【答案】C
【解析】本题考查“性别”对判断“人机大战是人类的胜利”这两个变量是否有关系,符合独立性检验的基本思想,因此,该题所选择的统计方法是独立性检验,故选C.
3.【答案】A
【解析】根据表中数据,可得,
代入线性回归方程中,求得,
则表中模糊不清的数据是,故选A.
4.【答案】D
【解析】由题意得,,,,,,
所以,,,,,则,
故选D.
5.【答案】B
【解析】由给出的四组数据的散点图可以看出,
图1和图3是正相关,相关系数大于0,则,,
图2和图4是负相关,相关系数小于0,则,,
图3和图4的点相对更加集中,所以相关性较强,所以接近于1,接近于,
图1和图2的点相对分散一些,所以相关性较弱,所以和比较接近0,
由此可得,故选B.
6.【答案】B
【解析】A.根据相关关系的定义,即可判断自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系,正确;
B.线性回归分析中,相关关系系数的绝对值越接近1,两个变量的线性相关性越强,错误;
C.残差图中,对于一组数据拟合程度的好坏评价,是残差点分别的带状区域宽度越狭窄,其模型拟合的精度越高,正确;
D.回归分析中,用相关系数刻画回归效果时,的值越大,说明模型的拟合效果越好,为的模型比为的模型拟合的效果好,正确,
故选B.
7.【答案】A
【解析】由散点图分布图可知,变量和成正相关,所以,,
在剔除点之后,且可看出回归直线的线性相关程度更强,更接近1.
所以,故选A.
8.【答案】A
【解析】因为与的线性回归方程为,
所以当时,,
由表格当广告支出万元时,销售额为万元,所以随机误差的效应(残差)为,故选A.
9.【答案】D
【解析】由表格得为,
因为在回归方程上且,
,解得,
,
当时,,故选D.
10.【答案】C
【解析】设,则,,
,所以.
令,得,故选C.
11.【答案】D
【解析】选项A:;
选项B:;
选项C:;
选项D:,
可得,
所以由选项D中的数据得到的值最大,说明与有关系的可能性最大,
故选D.
12.【答案】B
【解析】因为,,所以,
所以,故,故选B.
二、填空题:本大题共4小题,每小题5分.
13.【答案】②
【解析】①回归直线一定过中心点,可能不过任何一个样本点,①错;
②根据列列联表中的数据计算得出,而,则有99%的把握认为两个分类变量有关系,有1%的可能性使得“两个变量有关系”的推断出现错误,②正确;
③是用来判断两个分类变量是否相关的随机变量,的值的大小用来判断两变量相关性的可能性的大小,不是用来判断两变量是否相关,③错误,
故答案为②.
14.【答案】丁
【解析】越大,越小,线性相关性越强,
易知丁同学的试验结果体现A,B两变量的线性相关性较强,
故答案为丁.
15.【答案】6
【解析】因为,,
所以这组数据的样本中心点是,
把样本中心点代入回归方程,
所以,所以,故答案为6.
16.【答案】9
【解析】由题意知:,
则,
解得或,
因为且,,
综上得,,
所以,故答案为9.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1)4人,平均分为90;(2)列联表见解析,有的把握认为语文特别优秀的同学,数学也特别优秀.
【解析】(1)数学成绩特别优秀的概率为,
数学特别优秀的同学有人.
分.
(2)共有名文科学生参加考试,其中语文考试成绩低于的占,
语文成绩特别优秀的概率为,
语文特别优秀的同学有人,
列联表:
语文特别优秀
语文不特别优秀
合计
数学特别优秀
数学不特别优秀
合计
所以,
所以有的把握认为语文特别优秀的同学,数学也特别优秀.
18.【答案】(1),;(2);(3)没有.
【解析】(1)由题意得,所以,
200人的平均年龄为.
(2)由题意得:利用分层抽样的方法从第一组抽取2人,从第二组抽取3人,
记从第一组抽取的2人为,;从第二组抽取的3人为,,,
则从这5人中随机抽取2人的基本事件有,即10种,
其中两人恰好属于不同组别的基本事件有种,即6种,
故所求的概率.
(3)由题意可得列联表为:
购买力强人群
购买力弱人群
合计
青少年组
100
20
120
中老年组
60
20
80
合计
160
40
200
故的观测值,
故没有99%的把握认为是否属“购买力强人群”与年龄有关.
19.【答案】(1);(2)9(吨标准煤).
【解析】(1)由对应数据,计算得,,
,
所求的回归方程为.
(2),,
预测生产100吨甲产品的生产能耗比技改前降低(吨标准煤).
20.【答案】(1),25;(2)能在犯错误的概率不超过的条件下认为“中学生对航空航天的兴趣爱好和性别有关系”.
【解析】(1)时间的平均数为,
报名人数的平均数为,
所以,
,
所以线性回归方程为,
把代入得,所以第7天的报名人数约为25.
(2)由列联表数据可得,
因为,
所以,在犯错误的概率不超过的条件下认为“中学生对航空航天的兴趣爱好和性别有关系”.
21.【答案】(1)适宜;(2);(3)12千件产品.
【解析】(1)根据散点图判断,适宜作为非原料总成本y关于生产该产品的数量x的回归方程类型.
(2)由,两边同时取常用对数得.
设,∴,
∵,,,
∴.
把代入,得,
∴,∴,
∴,
即y关于x的回归方程为.
(3)设生产了x千件该产品.则生产总成本为.
又在其定义域内单调递增,且,
故最多能生产12千件产品.
22.【答案】(1)模型的拟合程度更好;(2)(ⅰ);(ⅱ).
【解析】(1)设和的相关系数为,和的相关系数为,
由题意,
;
,
则,因此从相关系数的角度,模型的拟合程度更好.
(2)(ⅰ)先建立关于的线性回归方程,
由,得,即,
,,
所以关于的线性回归方程为,
所以,则.
(ⅱ)2021年盈利额(亿元),
所以,则,
因为,
所以.
所以2021年的研发资金投入量约为亿元.
班级 姓名 准考证号 考场号 座位号
此卷只装订不密封
班级 姓名 准考证号 考场号 座位号
2020-2021学年度高中数学单元双基精品试卷
选修1-2第一章统计案例 (A)
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列关于回归分析与独立性检验的说法正确的是( )
①回归分析和独立性检验没有什么区别;
②回归分析是对两个变量准确关系的分析,而独立性检验是分析两个变量之间的不确定性关系;
③回归分析研究两个变量之间的相关关系,独立性检验是对两个变量是否具有某种关系的一种检验;
④独立性检验可以确定两个变量之间是否具有某种关系.
A.①② B.③ C.③④ D.全选
2.“人机大战,柯洁哭了,机器赢了”,2017年5月27日,19岁的世界围棋第一人柯洁不敌人工智能系统AlphaGo,落泪离席.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查.在参与调查的2600男性中,有1560人持反对意见,2400名女性中,有1118人持反对意见.再运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是( )
A.分层抽样 B.回归分析
C.独立性检验 D.频率分布直方图
3.为了研究某大型超市开业天数与销售额的情况,随机抽取了5天,其开业天数与每天的销售额的情况如表所示:
开业天数
10
20
30
40
50
销售额/天(万元)
62
75
81
89
根据上表提供的数据,求得关于的线性回归方程为,由于表中有一个数据模糊看不清,请你推断出该数据的值为( )
A. B. C. D.
4.某村庄对该村内名老年人、年轻人每年是否体检的情况进行了调查,统计数据如表所示:
每年体检
每年未体检
合计
老年人
年轻人
合计
已知抽取的老年人、年轻人各名,则对列联表数据的分析错误的是( )
A. B. C. D.
5.对四组数据进行统计,获得以下散点图,关于其线性相关系数比较,正确的是( )
A. B.
C. D.
6.下列说法错误的是( )
A.自变量取值一定时,因变量的取值有一定随机性的两个变量之间的关系叫做相关关系
B.在线性回归分析中,相关系数越大,变量间的相关性越强
C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D.在回归分析中,为的模型比为的模型拟合的效果好
7.下图是相关变量的散点图,现对这两个变量进行线性相关分析,方案一:根据图中所有数据,得到线性回归方程,相关系数为;方案二:剔除点,根据剩下数据,得到线性回归方程,相关系数为,则( )
A. B.
C. D.
8.某种产品的广告费支出与销售额(单位:万元)之间有如表关系,与的线性回归方程为,当广告支出5万元时,随机误差的效应(残差)为( )
2
4
5
6
8
30
40
60
50
70
A.10 B.20 C.30 D.40
9.某商场为了了解毛衣的月销售量(件)与月平均气温()之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温
17
13
8
2
月销售量(件)
24
33
40
55
由表中数据算出线性回归方程中的,气象部门预测下个月的平均气温为,据此估计该商场下个月毛衣销售量约为( )
A.58件 B.40件 C.38件 D.46件
10.2020年初,新型冠状病毒(COVID-19)引起的肺炎疫情爆发以来,各地医疗机构采取了各种针对性的治疗方法,取得了不错的成效,某地开始使用中西医结合方法后,每周治愈的患者人数如下表所示:
周数(x)
1
2
3
4
5
治愈人数(y)
2
17
36
93
142
由表格可得y关于x的二次回归方程为,则此回归模型第2周的残差(实际值与预报值之差)为( )
A.5 B.4 C.1 D.0
11.假设有两个分类变量和的列联表为:
????????
总计
总计
对同一样本,以下数据能说明与有关系的可能性最大的一组为( )
参考公式:,其中.
A. B.
C. D.
12.以模型去拟合一组数据时,为了求出回归方程,设,其变换后得到线性回归方程,则( )
A. B. C. D.
二、填空题:本大题共4小题,每小题5分.
13.下列说法中,正确的有_______.
①回归直线恒过点,且至少过一个样本点;
②根据列列联表中的数据计算得出,而,则有99%的把握认为两个分类变量有关系;
③是用来判断两个分类变量是否相关的随机变量,当的值很小时可以推断两个变量不相关.
14.甲?乙?丙?丁四位同学各自对A,B两个变量的线性相关性做试验,并用回归分析方法分别求得相关系数r与残差平方和m,如下表:
甲
乙
丙
丁
则________同学的试验结果体现A,B两变量有更强的线性相关性.
15.为了研究某种细菌在特定环境下,随时间变化繁殖情况,得如下实验数据,计算得回归方程为.由以上信息,得到下表中c的值为_________.
天数t(天)
繁殖个数y(千个)
16.有两个分类变量和,其中一组观测值为如下的2×2列联表:
总计
15
50
总计
20
45
65
其中,均为大于5的整数,则__________时,在犯错误的概率不超过的前提下为“和之间有关系”.附:.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)在一次模拟考试中,某校共有名文科学生参加考试,其中语文考试成绩低于的占,如果成绩不低于的为特别优秀,数学成绩的频率分布直方图如图.
(1)求数学成绩特别优秀的人数及数学成绩的平均分;
(2)如果语文和数学两科都特别优秀的共有人.根据以上数据,完成列联表,并分析是否有的把握认为语文特别优秀的同学,数学也特别优秀.
语文特别优秀
语文不特别优秀
合计
数学特别优秀
数学不特别优秀
合计
参考数据:①;
②
…
…
18.(12分)为激活国内消费市场,挽回疫情造成的损失,国家出台一系列的促进国内消费的优惠政策,某机构从某一电商的线上交易大数据中来跟踪调查消费者的购买力,界定3至8月份购买商品在5000元以上人群属“购买力强人群”,购买商品在5000元以下人群属“购买力弱人群”.现从电商平台消费人群中随机选出200人,发现这200人中属购买力强的人数占80%,并将这200人按年龄分组,记第1组,第2组,第3组,第4组,第5组,得到频率分布直方图,如图.
(1)求出频率分布直方图中的值和这200人的平均年龄;
(2)从第1,2组中用分层抽样的方法抽取5人,并再从这5人中随机抽取2人进行电话回访,求这两人恰好属于不同组别的概率;
(3)把年龄在第1,2,3组的居民称为青少年组,年龄在第4,5组的居民称为中老年组,若选出的200人中“购买力弱人群”的中老年人有20人,问是否有99%的把握认为是否属“购买力强人群”与年龄有关?
附:
,.
19.(12分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗(吨标准煤)的几组对应数据.
3
4
5
6
7
3
3
4
5
5
(1)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;
(2)已知该厂技改前,100吨甲产品的生产能耗为70吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低了多少吨标准煤?
参考公式,.
20.(12分)我国探月工程嫦娥五号探测器于2020年12月1日23时11分降落在月球表面预选着陆区,在顺利完成月面自动采样之后,成功将携带样品的上升器送入到预定环月轨道,这是我国首次实现月球无人采样和地外天体起飞,对我国航天事业具有重大而深远的影响,为进一步培养中学生对航空航天的兴趣爱好,某学校航空航天社团在本校高一年级进行了纳新工作,前五天的报名情况为:第1天3人,第2天6人,第3天10人,第4天13人,第5天18人,通过数据分析已知,报名人数与报名时间具有线性相关关系.
(1)已知第天的报名人数为,求关于的线性回归方程,并预测第7天的报名人数(结果四舍五入取整数);
(2)该社团为了解中学生对航空航天的兴趣爱好和性别是否有关系,随机调查了100名学生,并得到如下列联表:
有兴趣
无兴趣
合计
男生
45
5
50
女生
30
20
50
合计
75
25
100
请根据上面的列联表判断能否在犯错误的概率不超过的条件下认为“中学生对航空航天的兴趣爱好和性别有关系”.
参考公式及数据:回归方程中斜率的最小二乘估计公式为:,;
,其中.
21.(12分)某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每批产品的非原料总成本(元)与生产该产品的数量(千件)有关,经统计得到如下数据:
1
2
3
4
5
6
7
6
11
21
34
66
101
196
根据以上数据,绘制如图所示的散点图.
观察散点图,两个变量不具有线性相关关系,现考虑用对数函数模型和指数函数模型分别对两个变量的关系进行拟合.
(1)根据散点图判断,与(,均为大于零的常数)哪一个适宜作为非原料总成本关于生产该产品的数量的回归方程类型;(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表1中的数据,建立关于的回归方程;
(3)已知每件产品的原料成本为10元,若该产品的总成本不得高于123470元,请估计最多能生产多少千件产品.
参考数据:
其中,.
参考公式:对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计公式分别为,.
22.(12分)我国为全面建设社会主义现代化国家,制定了从2021年到2025年的“十四五”规划.某企业为响应国家号召,汇聚科研力量,加强科技创新,准备增加研发资金.现该企业为了了解年研发资金投入额(单位:亿元)对年盈利额(单位:亿元)的影响,研究了“十二五”和“十三五”规划发展期间近10年年研发资金投入额和年盈利额的数据.通过对比分析,建立了两个函数模型:①,②,其中,,,均为常数,为自然对数的底数.
令,,经计算得如下数据:
(1)请从相关系数的角度,分析哪一个模型拟合程度更好?
(2)(ⅰ)根据(1)的选择及表中数据,建立关于的回归方程;(系数精确到)
(ⅱ)若希望2021年盈利额为250亿元,请预测2021年的研发资金投入额为多少亿元?(结果精确到)
附:①相关系数,回归直线中:,.
②参考数据:,.
统计案例(A)答 案
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】B
【解析】回归分析是对两个变量之间的相关关系的一种分析,而相关关系是一种不确定关系,通过回归分析可能两个变量之间具有的相关关系.
而独立性检验是对两个变量之间是否具有某种关系的分析,并且可以分析这两个变量在多大程度上具有这种关系,但不能100%肯定这种关系,
故①②④错误,③正确,故选B.
2.【答案】C
【解析】本题考查“性别”对判断“人机大战是人类的胜利”这两个变量是否有关系,符合独立性检验的基本思想,因此,该题所选择的统计方法是独立性检验,故选C.
3.【答案】A
【解析】根据表中数据,可得,
代入线性回归方程中,求得,
则表中模糊不清的数据是,故选A.
4.【答案】D
【解析】由题意得,,,,,,
所以,,,,,则,
故选D.
5.【答案】B
【解析】由给出的四组数据的散点图可以看出,
图1和图3是正相关,相关系数大于0,则,,
图2和图4是负相关,相关系数小于0,则,,
图3和图4的点相对更加集中,所以相关性较强,所以接近于1,接近于,
图1和图2的点相对分散一些,所以相关性较弱,所以和比较接近0,
由此可得,故选B.
6.【答案】B
【解析】A.根据相关关系的定义,即可判断自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系,正确;
B.线性回归分析中,相关关系系数的绝对值越接近1,两个变量的线性相关性越强,错误;
C.残差图中,对于一组数据拟合程度的好坏评价,是残差点分别的带状区域宽度越狭窄,其模型拟合的精度越高,正确;
D.回归分析中,用相关系数刻画回归效果时,的值越大,说明模型的拟合效果越好,为的模型比为的模型拟合的效果好,正确,
故选B.
7.【答案】A
【解析】由散点图分布图可知,变量和成正相关,所以,,
在剔除点之后,且可看出回归直线的线性相关程度更强,更接近1.
所以,故选A.
8.【答案】A
【解析】因为与的线性回归方程为,
所以当时,,
由表格当广告支出万元时,销售额为万元,所以随机误差的效应(残差)为,故选A.
9.【答案】D
【解析】由表格得为,
因为在回归方程上且,
,解得,
,
当时,,故选D.
10.【答案】C
【解析】设,则,,
,所以.
令,得,故选C.
11.【答案】D
【解析】选项A:;
选项B:;
选项C:;
选项D:,
可得,
所以由选项D中的数据得到的值最大,说明与有关系的可能性最大,
故选D.
12.【答案】B
【解析】因为,,所以,
所以,故,故选B.
二、填空题:本大题共4小题,每小题5分.
13.【答案】②
【解析】①回归直线一定过中心点,可能不过任何一个样本点,①错;
②根据列列联表中的数据计算得出,而,则有99%的把握认为两个分类变量有关系,有1%的可能性使得“两个变量有关系”的推断出现错误,②正确;
③是用来判断两个分类变量是否相关的随机变量,的值的大小用来判断两变量相关性的可能性的大小,不是用来判断两变量是否相关,③错误,
故答案为②.
14.【答案】丁
【解析】越大,越小,线性相关性越强,
易知丁同学的试验结果体现A,B两变量的线性相关性较强,
故答案为丁.
15.【答案】6
【解析】因为,,
所以这组数据的样本中心点是,
把样本中心点代入回归方程,
所以,所以,故答案为6.
16.【答案】9
【解析】由题意知:,
则,
解得或,
因为且,,
综上得,,
所以,故答案为9.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1)4人,平均分为90;(2)列联表见解析,有的把握认为语文特别优秀的同学,数学也特别优秀.
【解析】(1)数学成绩特别优秀的概率为,
数学特别优秀的同学有人.
分.
(2)共有名文科学生参加考试,其中语文考试成绩低于的占,
语文成绩特别优秀的概率为,
语文特别优秀的同学有人,
列联表:
语文特别优秀
语文不特别优秀
合计
数学特别优秀
数学不特别优秀
合计
所以,
所以有的把握认为语文特别优秀的同学,数学也特别优秀.
18.【答案】(1),;(2);(3)没有.
【解析】(1)由题意得,所以,
200人的平均年龄为.
(2)由题意得:利用分层抽样的方法从第一组抽取2人,从第二组抽取3人,
记从第一组抽取的2人为,;从第二组抽取的3人为,,,
则从这5人中随机抽取2人的基本事件有,即10种,
其中两人恰好属于不同组别的基本事件有种,即6种,
故所求的概率.
(3)由题意可得列联表为:
购买力强人群
购买力弱人群
合计
青少年组
100
20
120
中老年组
60
20
80
合计
160
40
200
故的观测值,
故没有99%的把握认为是否属“购买力强人群”与年龄有关.
19.【答案】(1);(2)9(吨标准煤).
【解析】(1)由对应数据,计算得,,
,
所求的回归方程为.
(2),,
预测生产100吨甲产品的生产能耗比技改前降低(吨标准煤).
20.【答案】(1),25;(2)能在犯错误的概率不超过的条件下认为“中学生对航空航天的兴趣爱好和性别有关系”.
【解析】(1)时间的平均数为,
报名人数的平均数为,
所以,
,
所以线性回归方程为,
把代入得,所以第7天的报名人数约为25.
(2)由列联表数据可得,
因为,
所以,在犯错误的概率不超过的条件下认为“中学生对航空航天的兴趣爱好和性别有关系”.
21.【答案】(1)适宜;(2);(3)12千件产品.
【解析】(1)根据散点图判断,适宜作为非原料总成本y关于生产该产品的数量x的回归方程类型.
(2)由,两边同时取常用对数得.
设,∴,
∵,,,
∴.
把代入,得,
∴,∴,
∴,
即y关于x的回归方程为.
(3)设生产了x千件该产品.则生产总成本为.
又在其定义域内单调递增,且,
故最多能生产12千件产品.
22.【答案】(1)模型的拟合程度更好;(2)(ⅰ);(ⅱ).
【解析】(1)设和的相关系数为,和的相关系数为,
由题意,
;
,
则,因此从相关系数的角度,模型的拟合程度更好.
(2)(ⅰ)先建立关于的线性回归方程,
由,得,即,
,,
所以关于的线性回归方程为,
所以,则.
(ⅱ)2021年盈利额(亿元),
所以,则,
因为,
所以.
所以2021年的研发资金投入量约为亿元.
