2021学年度高中数学选修2-3第二章随机变量及其分布双基精品试卷 随机变量及其分布(A)(含答案)
文档属性
| 名称 | 2021学年度高中数学选修2-3第二章随机变量及其分布双基精品试卷 随机变量及其分布(A)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 00:00:00 | ||
图片预览




文档简介
-1123950339725此卷只装订不密封
班级 姓名 准考证号 考场号 座位号
此卷只装订不密封
班级 姓名 准考证号 考场号 座位号
2021学年度高中数学选修2-3第二章随机变量及其分布
双基精品试卷
随机变量及其分布(A)
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知某种产品的合格率是,合格品中的一级品率是.则这种产品的一级品率为( )
A. B. C. D.
2.已知随机变量的分布列如下:
ξ
0
1
2
P
a
b
c
其中成等差数列,则函数有且只有一个零点的概率为( )
A. B. C. D.
3.已知随机变量服从二项分布,若,,则( )
A. B. C. D.
4.若随机变量X的分布列如下所示:
且,则a、b的值分别是( )
A.04,01 B.01,04 C.03,02 D.02,03
5.电视机的使用寿命与显像管开关的次数有关,某品牌的电视机的显像管开关了次还能继续使用的概率是,开关了次后还能继续使用的概率是,则已经开关了次的电视机显像管还能继续使用到次的概率是( )
A. B. C. D.
6.设每个工作日甲?乙?丙?丁人需使用某种设备的概率分别为,,,,各人是否需使用设备相互独立,则同一工作日至少人需使用设备的概率为( )
A.025 B.030 C.031 D.035
7.将两颗骰子各掷一次,设事件“两个点数都不相同”,“至少出现一个5点”,则概率( )
A. B. C. D.
8.设随机变量,函数没有零点的概率是,
则( )
附:若,则,.
A. B. C. D.
9.已知在10件产品中可能存在次品,从中抽取2件检查,其中次品数为ξ,已知,且该产品的次品率不超过40%,则这10件产品的次品率为( )
A.10% B.20% C.30% D.40%
10.某大学进行“羽毛球”、“美术”、“音乐”三个社团选拔.某同学经过考核选拔通过该校的“羽毛球”“美术”、“音乐”三个社团的概率依次为,已知三个社团中他恰好能进入两个的概率为,假设该同学经过考核通过这三个社团选拔成功与否相互独立,则该同学一个社团都不能进入的概率为( )
A. B. C. D.
11.俄国著名飞机设计师埃格?西科斯基设计了世界上第一架四引擎飞机和第一种投入生产的直升机,当代著名的“黑鹰”直升机就是由西科斯基公司生产的.年,为了远程性和安全性上与美国波音竞争,欧洲空中客车公司设计并制造了,是一种有四台发动机的远程双过道宽体客机,取代只有两台发动机的.假设每一架飞机的引擎在飞行中出现故障率为,且各引擎是否有故障是独立的,已知飞机至少有个引擎正常运行,飞机就可成功飞行;飞机需要个引擎全部正常运行,飞机才能成功飞行.若要使飞机比飞机更安全,则飞机引擎的故障率应控制的范围是( )
A. B. C. D.
12.一只小虫从数轴上的原点出发爬行,若一次爬行过程中,小虫等概率地向前或向后爬行1个单位,设爬行次后小虫所在位置对应的数为随机变量,则下列说法错误的是( )
A. B.
C. D.
二、填空题:本大题共4小题,每小题5分.
13.投掷红、蓝两颗均匀的骰子,设事件:蓝色骰子的点数为5或6;事件:两骰子的点数之和大于8,则已知事件发生的条件下事件发生的概率______.
14.11分制乒乓球比赛,每赢一球得1分,当某局打成后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲乙两位同学进行单打比赛,假设甲发球时甲得分的概率为05,乙发球时乙得分的概率为06,各球的结果相互独立.在某局打成后,甲先发球,乙以获胜的概率为______.
15.在一个不透明的摸奖箱中有五个分别标有1,2,3,4,5号码的大小相同的小球,现甲?乙?丙三个人依次参加摸奖活动,规定:每个人连续有放回地摸三次,若得到的三个球编号之和恰为4的倍数,则算作获奖,记获奖的人数为,则的数学期望为___________.
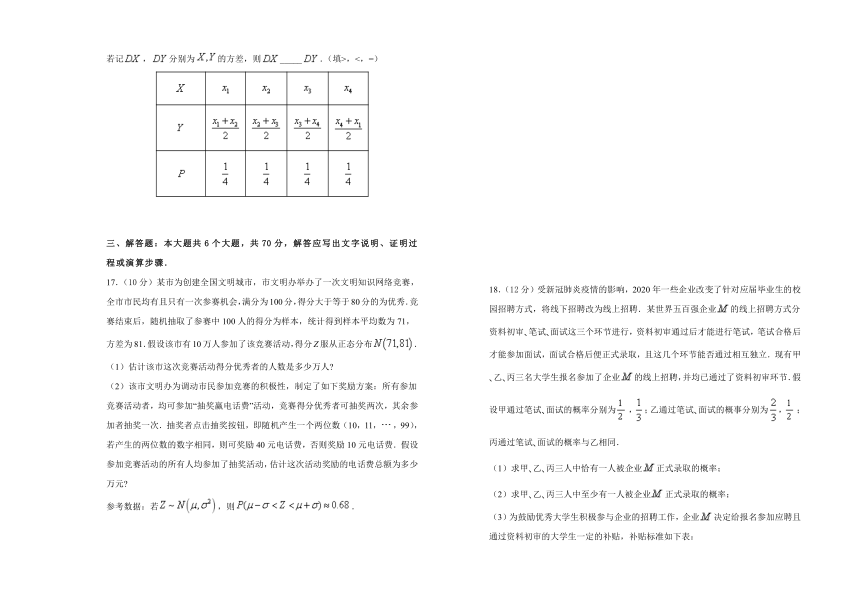
16.设为互不相等的正实数,随机变量和的分布列如下表,若记,分别为的方差,则_____.(填>,<,=)
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)某市为创建全国文明城市,市文明办举办了一次文明知识网络竞赛,全市市民均有且只有一次参赛机会,满分为100分,得分大于等于80分的为优秀.竞赛结束后,随机抽取了参赛中100人的得分为样本,统计得到样本平均数为71,方差为81.假设该市有10万人参加了该竞赛活动,得分Z服从正态分布.
(1)估计该市这次竞赛活动得分优秀者的人数是多少万人?
(2)该市文明办为调动市民参加竞赛的积极性,制定了如下奖励方案:所有参加竞赛活动者,均可参加“抽奖赢电话费”活动,竞赛得分优秀者可抽奖两次,其余参加者抽奖一次.抽奖者点击抽奖按钮,即随机产生一个两位数(10,11,,99),若产生的两位数的数字相同,则可奖励40元电话费,否则奖励10元电话费.假设参加竞赛活动的所有人均参加了抽奖活动,估计这次活动奖励的电话费总额为多少万元?
参考数据:若,则.
18.(12分)受新冠肺炎疫情的影响,2020年一些企业改变了针对应届毕业生的校园招聘方式,将线下招聘改为线上招聘.某世界五百强企业的线上招聘方式分资料初审?笔试?面试这三个环节进行,资料初审通过后才能进行笔试,笔试合格后才能参加面试,面试合格后便正式录取,且这几个环节能否通过相互独立.现有甲?乙?丙三名大学生报名参加了企业的线上招聘,并均已通过了资料初审环节.假设甲通过笔试?面试的概率分别为,;乙通过笔试?面试的概事分别为,;丙通过笔试?面试的概率与乙相同.
(1)求甲?乙?丙三人中恰有一人被企业正式录取的概率;
(2)求甲?乙?丙三人中至少有一人被企业正式录取的概率;
(3)为鼓励优秀大学生积极参与企业的招聘工作,企业决定给报名参加应聘且通过资料初审的大学生一定的补贴,补贴标准如下表:
参与环节
笔试
面试
补贴(元)
100
200
记甲?乙?丙三人获得的所有补贴之和为元,求的分布列和数学期望.
19.(12分)现有一堆颜色不同,形状一样的小球放入两个袋中,其中甲袋有5个红色小球,4个白色小球,乙袋中有4个红色小球,3个白色小球.
(1)分别从甲乙两袋中各取一个小球(相互无影响),求两个小球颜色不同的概率;
(2)先从两袋中任取一袋,然后在所取袋中任取一球,求取出为白球的概率;
(3)将两袋合为一袋,然后在袋中任取3球,设所取3个球中红球的个数为,求的分布列.
20.(12分)面对环境污染,党和政府高度重视,各级环保部门制定了严格措施治理污染,同时宣传部门加大保护环境的宣传力度,因此绿色低碳出行越来越成为市民的共识,为此吉安市在吉州区建立了公共自行车服务系统,市民凭本人二代身份证到公共自行车服务中心办理诚信借车卡,初次办卡时卡内预先赠送20分,当诚信积分为0时,借车卡自动锁定,限制借车,用户应持卡到公共自行车服务中心以1元购1个积分的形式再次激活该卡,为了鼓励市民租用公共自行车出行,同时督促市民尽快还车,方便更多的市民使用,公共自行车按每车每次的租用时间进行扣分缴费,具体扣分标准如下:①租用时间不超过1小时,免费;②租用时间为1小时以上且不超过2小时,扣1分;③租用时间为2小时以上且不超过3小时,扣2分;④租用时间为3小时以上且不超过4小时,扣3分;⑤租车时间超过4小时除扣3分外,超出时间按每小时扣2分收费(不足1小时的部分按1小时计算).甲?乙两人独立出行,各租用公共自行车一次,且两人租车时间都不会超过4小时,设甲?乙租用时间不超过一小时的概率分别是,;租用时间为1小时以上且不超过2小时的概率分别是,;租用时间为2小时以上且不超过3小时的概率分别是,.
(1)求甲比乙所扣积分多的概率;
(2)设甲?乙两人所扣积分之和为随机变量,求的分布列和数学期望.
21.(12分)一台设备由三个部件构成,假设在一天的运转中,部件1,2,3需要调整的概率分别为01,02,03,各部件的状态相互独立.
(1)求设备在一天的运转中,部件1,2中至少有1个需要调整的概率;
(2)记设备在一天的运转中需要调整的部件个数为,求的分布列及数学期望.
22.(12分)某电商平台联合手机厂家共同推出“分期购”服务,付款方式分为四个档次:1期、2期、3期和4期.记随机变量、分别表示顾客购买型手机和型手机的分期付款期数,根据以往销售数据统计,和的分布列如下表所示:
1
2
3
4
01
04
04
01
1
2
3
4
04
01
01
04
(1)若某位顾客购买型和手机各一部,求这位顾客两种手机都选择分4期付款的概率;
(2)电商平台销售一部型手机,若顾客选择分1期付款,则电商平台获得的利润为300元;若顾客选择分2期付款,则电商平台获得的利润为350元;若顾客选择分3期付款,则电商平台获得的利润为400元;若顾客选择分4期付款,则电商平台获得的利润为450元.记电商平台销售两部型手机所获得的利润为(单位:元),求的分布列;
(3)比较与的大小(只需写出结论).
随机变量及其分布(A)答 案
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】A
【解析】设事件为合格品,事件为一级品,则,,
则,故选A.
2.【答案】B
【解析】由题意知,且,解得,
又由函数有且只有一个零点,
即对于方程只有一个根,可得,解得,
所以,故选B.
3.【答案】A
【解析】由题意,解得,故选A.
4.【答案】B
【解析】由随机变量X的分布列得,
所以,
又因为,解得,
所以,故选B.
5.【答案】D
【解析】记事件电视机的显像管开关了次还能继续使用,
记事件电视机的显像管开关了次后还能继续使用,
则,,
所以,已经开关了次的电视机显像管还能继续使用到次的概率为,
故选D.
6.【答案】C
【解析】设甲?乙?丙?丁需使用设备分别为事件,,,,
则,,,
所以恰好人使用设备的概率为
,
人使用设备的概率,
故所求概率,故选C.
7.【答案】A
【解析】根据条件概率的含义,其含义为在发生的情况下,发生的概率,
即在“至少出现一个5点”的情况下,“两个点数都不相同”的概率,
“至少出现一个5点”的情况数目为,
“两个点数都不相同”则只有一个5点,共种,
故,故选A.
8.【答案】B
【解析】函数没有零点,二次方程无实根,
,,
又没有零点的概率是,,
由正态曲线的对称性知,
,,,
,
,,
,
故选B.
9.【答案】B
【解析】设10件产品中有x件次品,
则,所以x=2或8.
因为次品率不超过40%,所以x=2,
所以次品率为,故选B.
10.【答案】D
【解析】由题知,三个社团中他恰好能进入两个的概率为,
则,所以,
所以,
所以该同学一个社团都不进入的概率
,
故选D.
11.【答案】C
【解析】由题意,飞机引擎正常运行的概率为,
则飞机能成功飞行的概率为,
飞机能成功飞行的概率为,
令,即,解得,
所以飞机引擎的故障率应控制的范围是,故选C.
12.【答案】C
【解析】由题意知:设爬行次后小虫所在位置对应的数为随机变量,且小虫向前或向后爬行1个单位的概率均为,
∴爬行次后小虫一共向前爬行次,则向后爬行次,
有,
故,则,,故A、B正确;
,,即,有,故C错误;
,即,
有,故D正确,
故选C.
二、填空题:本大题共4小题,每小题5分.
13.【答案】
【解析】设为掷红骰子得的点数,为掷蓝骰子得的点数,则所有可能的事件与建立一一对应的关系,则共有36种基本事件,
事件:蓝色骰子的点数为5或6,有以下基本事件,,,,,,,,,,,共12个;
事件:两骰子的点数之和大于8,有以下基本事件,,,,,,,,,共10个,
故,,,
所以,故答案为.
14.【答案】015
【解析】依题意还需进行四场比赛,其中前两场乙输一场、最后两场乙赢,
其中发球方分别是甲、乙、甲、乙,
所以乙以获胜的概率,
故答案为.
15.【答案】
【解析】三个球编号之和恰为4的倍数的基本事件:有3种、有6种、有6种、有3种、有3种、有3种、有6种、有1种,
而总共有,
∴三个球编号之和恰为4的倍数的概率为,
由题意,∴的数学期望,
故答案为.
16.【答案】>
【解析】,
故
.
,
.
要比较的大小,只需比较与,
两者作差并化简得
①,
由于为互不相等的正实数,故,
也即,
也即,故答案为.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1)16(万人);(2)1508万元.
【解析】(1)因得分,所以标准差,所以优秀者得分,
由,得,
因此,估计这次参加竞赛活动得分优秀者的人数为(万人).
(2)设抽奖一次获得的话费为X元,
则,,
所以抽奖一次获得电话费的期望值为,
又由于10万人均参加抽奖,且优秀者参加两次,
所以抽奖总次数为万次,
因此,估计这次活动所需电话费为万元.
18.【答案】(1);(2);(3)分布列见解析,数学期望.
【解析】(1)设事件表示“甲被企业正式录取”,事件表示“乙被企业正式录取”,事件表示“丙被企业正式录取”,
则,,
所以甲?乙?丙三人中恰有一人被企业正式录取的概率
.
(2)设事件表示“甲、乙、丙三人都没有被企业正式录取”,
则,
所以甲?乙?丙三人中至少有一人被企业正式录取的概率.
(3)的所有可能取值为300,500,700,900,
,,
,.
所以的分布列为
300
500
700
900
.
19.【答案】(1);(2);(3)分布列见解析.
【解析】(1)设事件为“从甲袋中取出红球”,事件为“从乙袋中取出红球”,
事件为“两球颜色不同”,则,,
所以.
(2)设事件为“取出为白球”,事件为“取到甲袋”,事件为“取到乙袋”,
则,,,
则
.
(3)合为一袋后,有9个红球和7个白球,则的取值范围应为,
;;
;,
0
1
2
3
20.【答案】(1);(2)分布列见解析,数学期望.
【解析】(1)根据题意,分别记“甲扣分为0分?1分?2分?3分”为事件,,,,
它们彼此互斥,且,,,;
分别记“乙扣分为0分?1分?2分?3分”为事件,,,,
它们彼此互斥,且,,,,
由题知,事件,,,与事件,,,相互独立,
记甲比乙所扣积分多为事件,
则,
所以
.
(2)根据题的可能取值为:0,1,2,3,4,5,6,
则,
,
,
,
,
,
.
所以的分布列为:
0
1
2
3
4
5
6
的数学期望
.
21.【答案】(1)028;(2)分布列见解析,.
【解析】(1)设部件1需要调整为事件A,部件2需要调整为事件B,部件3需要调整为事件C,
由题意可知:,,.
部件1,2中至少有1个需要调整的概率为:
.
(2)由题意可知X的取值为0,1,2,3.
且
,
,
.
,
故X的分布列为:
0
1
2
3
其数学期望:.
22.【答案】(1);(2)见解析;(3).
【解析】(1)某位顾客购买型和手机是独立事件,
则这位顾客两种手机都选择分4期付款的概率为.
(2)的可能取值为,
,
,
,
,
,
,
,
则的分布列为
(3).
班级 姓名 准考证号 考场号 座位号
此卷只装订不密封
班级 姓名 准考证号 考场号 座位号
2021学年度高中数学选修2-3第二章随机变量及其分布
双基精品试卷
随机变量及其分布(A)
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知某种产品的合格率是,合格品中的一级品率是.则这种产品的一级品率为( )
A. B. C. D.
2.已知随机变量的分布列如下:
ξ
0
1
2
P
a
b
c
其中成等差数列,则函数有且只有一个零点的概率为( )
A. B. C. D.
3.已知随机变量服从二项分布,若,,则( )
A. B. C. D.
4.若随机变量X的分布列如下所示:
且,则a、b的值分别是( )
A.04,01 B.01,04 C.03,02 D.02,03
5.电视机的使用寿命与显像管开关的次数有关,某品牌的电视机的显像管开关了次还能继续使用的概率是,开关了次后还能继续使用的概率是,则已经开关了次的电视机显像管还能继续使用到次的概率是( )
A. B. C. D.
6.设每个工作日甲?乙?丙?丁人需使用某种设备的概率分别为,,,,各人是否需使用设备相互独立,则同一工作日至少人需使用设备的概率为( )
A.025 B.030 C.031 D.035
7.将两颗骰子各掷一次,设事件“两个点数都不相同”,“至少出现一个5点”,则概率( )
A. B. C. D.
8.设随机变量,函数没有零点的概率是,
则( )
附:若,则,.
A. B. C. D.
9.已知在10件产品中可能存在次品,从中抽取2件检查,其中次品数为ξ,已知,且该产品的次品率不超过40%,则这10件产品的次品率为( )
A.10% B.20% C.30% D.40%
10.某大学进行“羽毛球”、“美术”、“音乐”三个社团选拔.某同学经过考核选拔通过该校的“羽毛球”“美术”、“音乐”三个社团的概率依次为,已知三个社团中他恰好能进入两个的概率为,假设该同学经过考核通过这三个社团选拔成功与否相互独立,则该同学一个社团都不能进入的概率为( )
A. B. C. D.
11.俄国著名飞机设计师埃格?西科斯基设计了世界上第一架四引擎飞机和第一种投入生产的直升机,当代著名的“黑鹰”直升机就是由西科斯基公司生产的.年,为了远程性和安全性上与美国波音竞争,欧洲空中客车公司设计并制造了,是一种有四台发动机的远程双过道宽体客机,取代只有两台发动机的.假设每一架飞机的引擎在飞行中出现故障率为,且各引擎是否有故障是独立的,已知飞机至少有个引擎正常运行,飞机就可成功飞行;飞机需要个引擎全部正常运行,飞机才能成功飞行.若要使飞机比飞机更安全,则飞机引擎的故障率应控制的范围是( )
A. B. C. D.
12.一只小虫从数轴上的原点出发爬行,若一次爬行过程中,小虫等概率地向前或向后爬行1个单位,设爬行次后小虫所在位置对应的数为随机变量,则下列说法错误的是( )
A. B.
C. D.
二、填空题:本大题共4小题,每小题5分.
13.投掷红、蓝两颗均匀的骰子,设事件:蓝色骰子的点数为5或6;事件:两骰子的点数之和大于8,则已知事件发生的条件下事件发生的概率______.
14.11分制乒乓球比赛,每赢一球得1分,当某局打成后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲乙两位同学进行单打比赛,假设甲发球时甲得分的概率为05,乙发球时乙得分的概率为06,各球的结果相互独立.在某局打成后,甲先发球,乙以获胜的概率为______.
15.在一个不透明的摸奖箱中有五个分别标有1,2,3,4,5号码的大小相同的小球,现甲?乙?丙三个人依次参加摸奖活动,规定:每个人连续有放回地摸三次,若得到的三个球编号之和恰为4的倍数,则算作获奖,记获奖的人数为,则的数学期望为___________.
16.设为互不相等的正实数,随机变量和的分布列如下表,若记,分别为的方差,则_____.(填>,<,=)
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)某市为创建全国文明城市,市文明办举办了一次文明知识网络竞赛,全市市民均有且只有一次参赛机会,满分为100分,得分大于等于80分的为优秀.竞赛结束后,随机抽取了参赛中100人的得分为样本,统计得到样本平均数为71,方差为81.假设该市有10万人参加了该竞赛活动,得分Z服从正态分布.
(1)估计该市这次竞赛活动得分优秀者的人数是多少万人?
(2)该市文明办为调动市民参加竞赛的积极性,制定了如下奖励方案:所有参加竞赛活动者,均可参加“抽奖赢电话费”活动,竞赛得分优秀者可抽奖两次,其余参加者抽奖一次.抽奖者点击抽奖按钮,即随机产生一个两位数(10,11,,99),若产生的两位数的数字相同,则可奖励40元电话费,否则奖励10元电话费.假设参加竞赛活动的所有人均参加了抽奖活动,估计这次活动奖励的电话费总额为多少万元?
参考数据:若,则.
18.(12分)受新冠肺炎疫情的影响,2020年一些企业改变了针对应届毕业生的校园招聘方式,将线下招聘改为线上招聘.某世界五百强企业的线上招聘方式分资料初审?笔试?面试这三个环节进行,资料初审通过后才能进行笔试,笔试合格后才能参加面试,面试合格后便正式录取,且这几个环节能否通过相互独立.现有甲?乙?丙三名大学生报名参加了企业的线上招聘,并均已通过了资料初审环节.假设甲通过笔试?面试的概率分别为,;乙通过笔试?面试的概事分别为,;丙通过笔试?面试的概率与乙相同.
(1)求甲?乙?丙三人中恰有一人被企业正式录取的概率;
(2)求甲?乙?丙三人中至少有一人被企业正式录取的概率;
(3)为鼓励优秀大学生积极参与企业的招聘工作,企业决定给报名参加应聘且通过资料初审的大学生一定的补贴,补贴标准如下表:
参与环节
笔试
面试
补贴(元)
100
200
记甲?乙?丙三人获得的所有补贴之和为元,求的分布列和数学期望.
19.(12分)现有一堆颜色不同,形状一样的小球放入两个袋中,其中甲袋有5个红色小球,4个白色小球,乙袋中有4个红色小球,3个白色小球.
(1)分别从甲乙两袋中各取一个小球(相互无影响),求两个小球颜色不同的概率;
(2)先从两袋中任取一袋,然后在所取袋中任取一球,求取出为白球的概率;
(3)将两袋合为一袋,然后在袋中任取3球,设所取3个球中红球的个数为,求的分布列.
20.(12分)面对环境污染,党和政府高度重视,各级环保部门制定了严格措施治理污染,同时宣传部门加大保护环境的宣传力度,因此绿色低碳出行越来越成为市民的共识,为此吉安市在吉州区建立了公共自行车服务系统,市民凭本人二代身份证到公共自行车服务中心办理诚信借车卡,初次办卡时卡内预先赠送20分,当诚信积分为0时,借车卡自动锁定,限制借车,用户应持卡到公共自行车服务中心以1元购1个积分的形式再次激活该卡,为了鼓励市民租用公共自行车出行,同时督促市民尽快还车,方便更多的市民使用,公共自行车按每车每次的租用时间进行扣分缴费,具体扣分标准如下:①租用时间不超过1小时,免费;②租用时间为1小时以上且不超过2小时,扣1分;③租用时间为2小时以上且不超过3小时,扣2分;④租用时间为3小时以上且不超过4小时,扣3分;⑤租车时间超过4小时除扣3分外,超出时间按每小时扣2分收费(不足1小时的部分按1小时计算).甲?乙两人独立出行,各租用公共自行车一次,且两人租车时间都不会超过4小时,设甲?乙租用时间不超过一小时的概率分别是,;租用时间为1小时以上且不超过2小时的概率分别是,;租用时间为2小时以上且不超过3小时的概率分别是,.
(1)求甲比乙所扣积分多的概率;
(2)设甲?乙两人所扣积分之和为随机变量,求的分布列和数学期望.
21.(12分)一台设备由三个部件构成,假设在一天的运转中,部件1,2,3需要调整的概率分别为01,02,03,各部件的状态相互独立.
(1)求设备在一天的运转中,部件1,2中至少有1个需要调整的概率;
(2)记设备在一天的运转中需要调整的部件个数为,求的分布列及数学期望.
22.(12分)某电商平台联合手机厂家共同推出“分期购”服务,付款方式分为四个档次:1期、2期、3期和4期.记随机变量、分别表示顾客购买型手机和型手机的分期付款期数,根据以往销售数据统计,和的分布列如下表所示:
1
2
3
4
01
04
04
01
1
2
3
4
04
01
01
04
(1)若某位顾客购买型和手机各一部,求这位顾客两种手机都选择分4期付款的概率;
(2)电商平台销售一部型手机,若顾客选择分1期付款,则电商平台获得的利润为300元;若顾客选择分2期付款,则电商平台获得的利润为350元;若顾客选择分3期付款,则电商平台获得的利润为400元;若顾客选择分4期付款,则电商平台获得的利润为450元.记电商平台销售两部型手机所获得的利润为(单位:元),求的分布列;
(3)比较与的大小(只需写出结论).
随机变量及其分布(A)答 案
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】A
【解析】设事件为合格品,事件为一级品,则,,
则,故选A.
2.【答案】B
【解析】由题意知,且,解得,
又由函数有且只有一个零点,
即对于方程只有一个根,可得,解得,
所以,故选B.
3.【答案】A
【解析】由题意,解得,故选A.
4.【答案】B
【解析】由随机变量X的分布列得,
所以,
又因为,解得,
所以,故选B.
5.【答案】D
【解析】记事件电视机的显像管开关了次还能继续使用,
记事件电视机的显像管开关了次后还能继续使用,
则,,
所以,已经开关了次的电视机显像管还能继续使用到次的概率为,
故选D.
6.【答案】C
【解析】设甲?乙?丙?丁需使用设备分别为事件,,,,
则,,,
所以恰好人使用设备的概率为
,
人使用设备的概率,
故所求概率,故选C.
7.【答案】A
【解析】根据条件概率的含义,其含义为在发生的情况下,发生的概率,
即在“至少出现一个5点”的情况下,“两个点数都不相同”的概率,
“至少出现一个5点”的情况数目为,
“两个点数都不相同”则只有一个5点,共种,
故,故选A.
8.【答案】B
【解析】函数没有零点,二次方程无实根,
,,
又没有零点的概率是,,
由正态曲线的对称性知,
,,,
,
,,
,
故选B.
9.【答案】B
【解析】设10件产品中有x件次品,
则,所以x=2或8.
因为次品率不超过40%,所以x=2,
所以次品率为,故选B.
10.【答案】D
【解析】由题知,三个社团中他恰好能进入两个的概率为,
则,所以,
所以,
所以该同学一个社团都不进入的概率
,
故选D.
11.【答案】C
【解析】由题意,飞机引擎正常运行的概率为,
则飞机能成功飞行的概率为,
飞机能成功飞行的概率为,
令,即,解得,
所以飞机引擎的故障率应控制的范围是,故选C.
12.【答案】C
【解析】由题意知:设爬行次后小虫所在位置对应的数为随机变量,且小虫向前或向后爬行1个单位的概率均为,
∴爬行次后小虫一共向前爬行次,则向后爬行次,
有,
故,则,,故A、B正确;
,,即,有,故C错误;
,即,
有,故D正确,
故选C.
二、填空题:本大题共4小题,每小题5分.
13.【答案】
【解析】设为掷红骰子得的点数,为掷蓝骰子得的点数,则所有可能的事件与建立一一对应的关系,则共有36种基本事件,
事件:蓝色骰子的点数为5或6,有以下基本事件,,,,,,,,,,,共12个;
事件:两骰子的点数之和大于8,有以下基本事件,,,,,,,,,共10个,
故,,,
所以,故答案为.
14.【答案】015
【解析】依题意还需进行四场比赛,其中前两场乙输一场、最后两场乙赢,
其中发球方分别是甲、乙、甲、乙,
所以乙以获胜的概率,
故答案为.
15.【答案】
【解析】三个球编号之和恰为4的倍数的基本事件:有3种、有6种、有6种、有3种、有3种、有3种、有6种、有1种,
而总共有,
∴三个球编号之和恰为4的倍数的概率为,
由题意,∴的数学期望,
故答案为.
16.【答案】>
【解析】,
故
.
,
.
要比较的大小,只需比较与,
两者作差并化简得
①,
由于为互不相等的正实数,故,
也即,
也即,故答案为.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1)16(万人);(2)1508万元.
【解析】(1)因得分,所以标准差,所以优秀者得分,
由,得,
因此,估计这次参加竞赛活动得分优秀者的人数为(万人).
(2)设抽奖一次获得的话费为X元,
则,,
所以抽奖一次获得电话费的期望值为,
又由于10万人均参加抽奖,且优秀者参加两次,
所以抽奖总次数为万次,
因此,估计这次活动所需电话费为万元.
18.【答案】(1);(2);(3)分布列见解析,数学期望.
【解析】(1)设事件表示“甲被企业正式录取”,事件表示“乙被企业正式录取”,事件表示“丙被企业正式录取”,
则,,
所以甲?乙?丙三人中恰有一人被企业正式录取的概率
.
(2)设事件表示“甲、乙、丙三人都没有被企业正式录取”,
则,
所以甲?乙?丙三人中至少有一人被企业正式录取的概率.
(3)的所有可能取值为300,500,700,900,
,,
,.
所以的分布列为
300
500
700
900
.
19.【答案】(1);(2);(3)分布列见解析.
【解析】(1)设事件为“从甲袋中取出红球”,事件为“从乙袋中取出红球”,
事件为“两球颜色不同”,则,,
所以.
(2)设事件为“取出为白球”,事件为“取到甲袋”,事件为“取到乙袋”,
则,,,
则
.
(3)合为一袋后,有9个红球和7个白球,则的取值范围应为,
;;
;,
0
1
2
3
20.【答案】(1);(2)分布列见解析,数学期望.
【解析】(1)根据题意,分别记“甲扣分为0分?1分?2分?3分”为事件,,,,
它们彼此互斥,且,,,;
分别记“乙扣分为0分?1分?2分?3分”为事件,,,,
它们彼此互斥,且,,,,
由题知,事件,,,与事件,,,相互独立,
记甲比乙所扣积分多为事件,
则,
所以
.
(2)根据题的可能取值为:0,1,2,3,4,5,6,
则,
,
,
,
,
,
.
所以的分布列为:
0
1
2
3
4
5
6
的数学期望
.
21.【答案】(1)028;(2)分布列见解析,.
【解析】(1)设部件1需要调整为事件A,部件2需要调整为事件B,部件3需要调整为事件C,
由题意可知:,,.
部件1,2中至少有1个需要调整的概率为:
.
(2)由题意可知X的取值为0,1,2,3.
且
,
,
.
,
故X的分布列为:
0
1
2
3
其数学期望:.
22.【答案】(1);(2)见解析;(3).
【解析】(1)某位顾客购买型和手机是独立事件,
则这位顾客两种手机都选择分4期付款的概率为.
(2)的可能取值为,
,
,
,
,
,
,
,
则的分布列为
(3).
