2021学年度高中数学选修2-3第三章统计案例双基精品试卷 统计案例(B)(含答案)
文档属性
| 名称 | 2021学年度高中数学选修2-3第三章统计案例双基精品试卷 统计案例(B)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 00:00:00 | ||
图片预览



文档简介
-1123950339725此卷只装订不密封
班级 姓名 准考证号 考场号 座位号
此卷只装订不密封
班级 姓名 准考证号 考场号 座位号
2021学年度高中数学选修2-3第三章统计案例双基精品试卷
统计案例(B)
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是( )
A. B.
C. D.
2.为了解学生对街舞的喜欢是否与性别有关,在全校学生中进行抽样调查,根据数据,求得的观测值,则至少有( )的把握认为对街舞的喜欢与性别有关.参考数据:
A. B. C. D.
3.为检测某药品服用后的多长时间开始有药物反应,现随机抽取服用了该药品的1000人,其服用后开始有药物反应的时间(分钟)与人数的数据绘成的频率分布直方图如图所示.若将直方图中分组区间的中点值设为解释变量(分钟),这个区间上的人数为(人),易见两变量,线性相关,那么一定在其线性回归直线上的点为( )
A. B. C. D.
4.2015年年岁史诗大剧《芈月传》风靡大江南北,影响力不亚于以前的《甄嬛传》.某记者调查了大量《芈月传》的观众,发现年龄段与爱看的比例存在较好的线性相关关系,年龄在,,,,的爱看比例分别为,,,,.现用这5个年龄段的中间值代表年龄段,如12代表,代表,根据前四个数据求得关于爱看比例的线性回归方程为,由此可推测的值为( )
A. B. C. D.
5.某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系,随机抽查52名中学生,得到统计数据如表1至表4,这与性别有关联的可能性最大的变量是( )
A.成绩 B.视力 C.智商 D.阅读量
6.为预测某种产品的回收率y,需要研究它和原料有效成分的含量x之间的相关关系,现取了8组观察值.计算得,,,,则y对x的回归方程是( )
A. B.
C. D.
7.某饮料店的日销售收入(单位:百元)与当天平均气温(单位:)之间有下列数据:
0
1
2
4
2
2
1
甲、乙、丙三位同学对上述数据进行研究,分别得到了与之间的四个线性回归方程,其中正确的是( )
A. B.
C. D.
8.变量与相对应的一组数据为,,,,;变量与相对应的一组数据为,,,,.表示变量,之间的线性相关系数,表示变量与之间的线性相关系数,则( )
A. B. C. D.
9.某商场为了了解不同厂家生产的散装面包的月销售量(千克)与售价(元/千克)之间的关系,随机统计了某几个月的月销售量与当月各散装面包的售价,相关数据如下表:
售价(元/千克)
月销售量(千克)
由表中数据算出线性回归方程为,则样本在处的残差为( )
A. B. C. D.
10.下列有关线性回归分析的六个命题:
①线性回归直线必过样本数据的中心点;
②回归直线就是散点图中经过样本数据点最多的那条直线;
③当相关性系数时,两个变量正相关;
④如果两个变量的相关性越强,则相关性系数就越接近于1;
⑤残差图中残差点所在的水平带状区域越宽,则回归方程的预报精确度越高;
⑥甲、乙两个模型的分别约为和,则模型乙的拟合效果更好.
其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
11.假设2个分类变量X和Y的2×2列联表如下:
Y
X
y1
y2
总计
x1
a
10
a+10
x2
c
30
c+30
总计
a+c
40
100
对于同一样本,以下数据能说明和有关系的可能性最大的一组是( )
A., B.,
C., D.,
12.下列四个命题:
①在回归模型中,预报变量y的值不能由解释变量x唯一确定;
②若变量x,y满足关系,且变量y与z正相关,则x与z也正相关;
③在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;
④以模型去拟合一组数据时,为了求出回归方程,设,将其变换后得到线性方程,则,.
其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题:本大题共4小题,每小题5分.
13.已知x、y之间的一组数据如下:
x
0
1
2
3
y
8
2
6
4
则线性回归方程所表示的直线必经过点________.
14.如图所示是世界20个地区受教育程度的人口百分比与人均收入的散点图,样本点基本集中在一个条型区域,因此两个变量呈线性相关关系.利用散点图中的数据建立的回归方程为,若受教育的人口百分比相差10%,则其人均收入相差_________.
15.已知如下四个命题:①在线性回归模型中,相关指数表示解释变量对于预报变量的贡献率,越接近于,表示回归效果越好;②在回归直线方程中,当解释变量每增加一个单位时,预报变量平均增加个单位;③两个变量相关性越强,则相关系数的绝对值就越接近于;④对分类变量与,对它们的随机变量的观测值来说,越小,则“与有关系”的把握程度越大.其中正确命题的序号是__________.
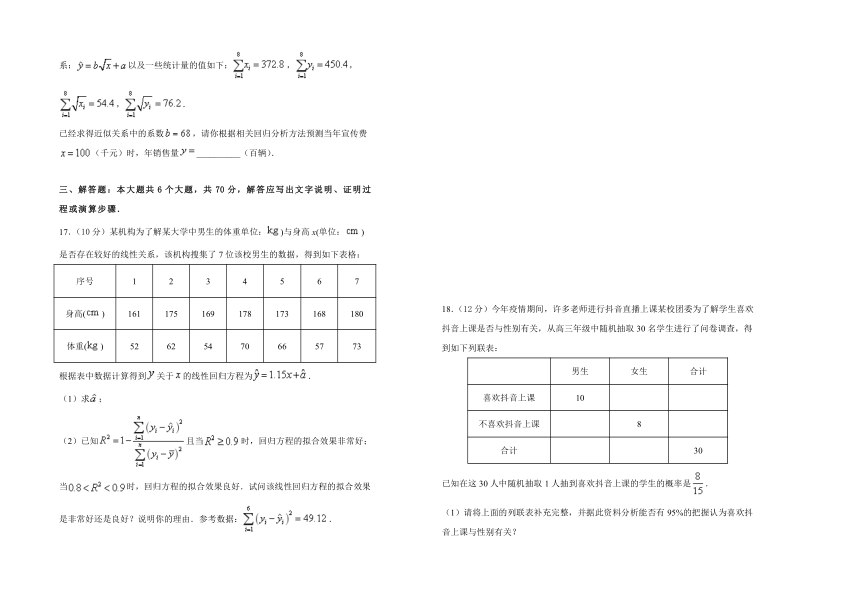
16.某汽车销售公司为确定下一年度投入某种产品的宣传费,需了解年宣传费(单位:千元)对年销售量(单位:百辆)的影响,对近8年的年宣传费和年销售量数据作了初步处理,得到年销售量与年宣传费具有近似关系:以及一些统计量的值如下:,,,.
已经求得近似关系中的系数,请你根据相关回归分析方法预测当年宣传费(千元)时,年销售量__________(百辆).
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)某机构为了解某大学中男生的体重单位:)与身高x(单位:)是否存在较好的线性关系,该机构搜集了7位该校男生的数据,得到如下表格:
序号
1
2
3
4
5
6
7
身高()
161
175
169
178
173
168
180
体重()
52
62
54
70
66
57
73
根据表中数据计算得到关于的线性回归方程为.
(1)求;
(2)已知且当时,回归方程的拟合效果非常好;当时,回归方程的拟合效果良好.试问该线性回归方程的拟合效果是非常好还是良好?说明你的理由.参考数据:.
18.(12分)今年疫情期间,许多老师进行抖音直播上课某校团委为了解学生喜欢抖音上课是否与性别有关,从高三年级中随机抽取30名学生进行了问卷调查,得到如下列联表:
男生
女生
合计
喜欢抖音上课
10
不喜欢抖音上课
8
合计
30
已知在这30人中随机抽取1人抽到喜欢抖音上课的学生的概率是.
(1)请将上面的列联表补充完整,并据此资料分析能否有95%的把握认为喜欢抖音上课与性别有关?
(2)若从这30人中的女生中随机抽取2人,记喜欢抖音上课的人数为X,求X的分布列、数学期望.
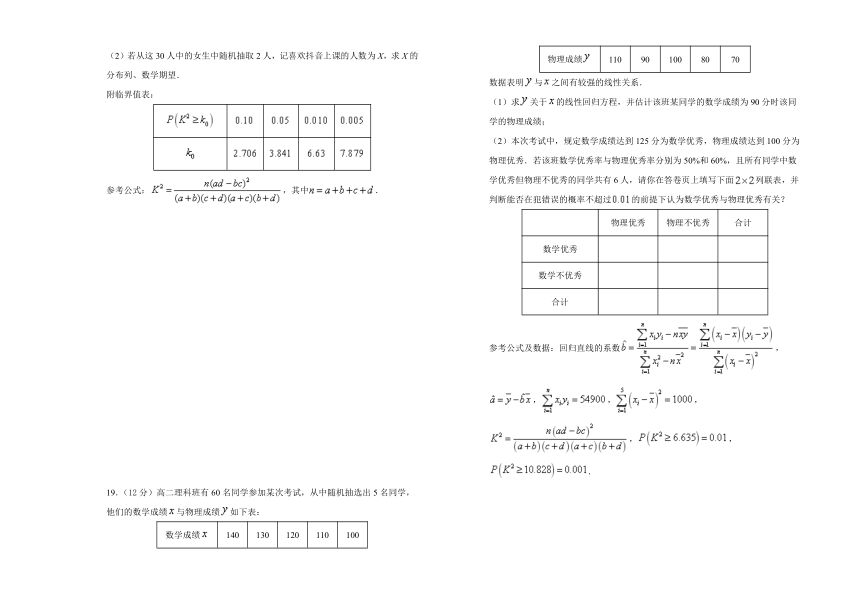
附临界值表:
参考公式:,其中.
19.(12分)高二理科班有60名同学参加某次考试,从中随机抽选出5名同学,他们的数学成绩与物理成绩如下表:
数学成绩
140
130
120
110
100
物理成绩
110
90
100
80
70
数据表明与之间有较强的线性关系.
(1)求关于的线性回归方程,并估计该班某同学的数学成绩为90分时该同学的物理成绩;
(2)本次考试中,规定数学成绩达到125分为数学优秀,物理成绩达到100分为物理优秀.若该班数学优秀率与物理优秀率分别为50%和60%,且所有同学中数学优秀但物理不优秀的同学共有6人,请你在答卷页上填写下面列联表,并判断能否在犯错误的概率不超过的前提下认为数学优秀与物理优秀有关?
物理优秀
物理不优秀
合计
数学优秀
数学不优秀
合计
参考公式及数据:回归直线的系数,,,,,,.
20.(12分)学校食堂统计了最近天到餐厅就餐的人数(百人)与食堂向食材公司购买所需食材(原材料)的数量(袋),得到如下统计表:
第一天
第二天
第三天
第四天
第五天
就餐人数(百人)
13
9
8
10
12
原材料(袋)
32
23
18
24
28
(1)根据所给的组数据,求出关于的线性回归方程;
(2)已知购买食材的费用(元)与数量(袋)的关系为,投入使用的每袋食材相应的销售单价为元,多余的食材必须无偿退还食材公司,据悉下周一大约有人到食堂餐厅就餐,根据(1)中求出的线性回归方程,预测食堂应购买多少袋食材,才能获得最大利润,最大利润是多少?(注:利润L =销售收入-原材料费用)
参考公式:,,
参考数据:,,.
21.(12分)2019年的“金九银十”变成“铜九铁十”,国各地房价“跳水”严重,但某地二手房交易却“逆市”而行.如图是该地某小区2018年11月至2019年1月间,当月在售二手房均价(单位:万元平方米)的散点图.(图中月份代码1~13分别对应2018年11月~2019年11月)
根据散点图选择和两个模型进行拟合,经过数据处理得到两个回归方程分别为和,并得到以下一些统计量的值:
(1)请利用相关指数判断哪个模型的拟合效果更好;
(2)某位购房者拟于2020年4月购买这个小区平方米的二手房(欲购房为其家庭首套房).
若购房时该小区所有住房的房产证均已满2但未满5年,请你利用(1)中拟合效果更好的模型解决以下问题:
(i)估算该购房者应支付的购房金额;(购房金额房款税费,房屋均价精确到万元平方米);
(ii)若该购房者拟用不超过100万元的资金购买该小区一套二手房,试估算其可购买的最大面积.(精确到1平方米)
附注:根据有关规定,二手房交易需要缴纳若干项税费,税费是按房屋的计税价格(计税价格房款)进行征收的.
房产证满2年但未满5年的征收方式如下:首套面积90平方米以内(含90平方米)为;首套面积90平方米以上且140平方米以内(含140平方米);首套面积140平方米以上或非首套为.
参考数据:,,,,,,,.
参考公式:相关指数.
22.(12分)根据国家统计局数据,1999年至2019年我国进出口贸易总额从3万亿元跃升至万亿元,中国在国际市场上的贸易份额越来越大对外贸易在国民经济中的作用日益突出.将年份1999,2004,2009,2014,2019分别用1,2,3,4,5代替,并表示为,表示全国进出口贸易总额.
(1)根据以上统计数据及图表,给出了下列两个方案,请解决方案1中的问题.
方案1:用作为全国进出口贸易总额关于的回归方程,根据以下参考数据,求出关于的回归方程,并求相关指数.
方案2:用作为全国进出口贸易总额关于的回归方程,求得回归方程,相关指数.
(2)通过对比(1)中两个方案的相关指数,你认为哪个方案中的回归方程更合适,并利用此回归方程预测2020年全国进出口贸易总额.
参考数据:
①;②;③;④.
参考公式:线性回归方程中的斜率和截距的最小二乘法估计公式分别为:,,相关指数.
统计案例(B)答 案
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】A
【解析】因为商品销售量与销售价格负相关,所以排除B,D选项,
将代入,可得,不符合实际,故A正确.
2.【答案】B
【解析】因为,所以有的把握认为对街舞的喜欢与性别有关.
3.【答案】C
【解析】由频率分布直方图可知,第一个区间中点坐标,,
第二个区间中点坐标,,
第三个区间中点坐标,,
第四个区间中点坐标,,
则,,
则一定在其线性回归直线上的点为,故选C.
4.【答案】B
【解析】前4个数据对应的,(把百分数转化为小数),
而,
,,,
当,.
5.【答案】D
【解析】由表中数据可得
表1:;
表2:;
表3:;
表4:.
其中最大,所以阅读量与性别有关联的可能性最大,故D正确.
6.【答案】A
【解析】由,,直接计算得,,
所以,选A.
7.【答案】A
【解析】由题意可知,,
由回归方程过中心点,代入选项中只有A项满足.
8.【答案】C
【解析】变量与相对应的一组数据为,,,,,
,,
即;
变量与相对应的一组数据为,,,,,
,
这一组数据的相关系数,
则第一组数据的相关系数大于,第二组数据的相关系数小于,
则,故选C.
9.【答案】B
【解析】由表格得为,
又回归直线方程经过样本中心点,
所以,解得,
所以回归直线方程为,
把代入回归直线方程可得,
故样本在处的残差为,故选B.
10.【答案】B
【解析】①线性回归直线必过样本数据中心点,故①正确;
②回归直线方程在散点图中可能不经过任意样本数据点,故②错误;
③当相关性系数时,则两个变量正相关,故③正确;
④如果两个变量的相关性越强,则相关性系数就越接近于1或,故④错误;
⑤残差图中残差点所在的水平带状区域越窄,回归方程的预报精确度越高,
故⑤错误;
⑥甲、乙两个模型的分别约为和,则模型甲的拟合效果更好,
故⑥错误,
真命题的个数为,故选B.
11.【答案】B
【解析】的观测值,
根据2×2列联表和独立性检验的相关知识,当,一定时,,相差越大,
与相差就越大,就越大,即和有关系的可能性越大,
选项B中,与其它选项相比相差最大,故选B.
12.【答案】C
【解析】下列四个命题:
①在回归模型中,预报变量y的值不能由解释变量x唯一确定;根据回归模型中的变量关系,正确;
②若变量x,y满足关系,且变量y与z正相关,则x与z也正相关;应该是负相关,故错误;
③在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高,即越接近于回归直线的距离越小,故正确;
④以模型去拟合一组数据时,为了求出回归方程,设,将其变换后得到线性方程,则,,故正确,
故选C.
二、填空题:本大题共4小题,每小题5分.
13.【答案】
【解析】由题意可得,,
线性回归方程过样本中心点,即线性回归方程所表示的直线必经过点.
14.【答案】美元
【解析】设所受教育百分比分别为,,且,
根据回归方程为,
收入相差大约为,
即受教育的人口百分比相差,则其人均收入相差约美元,
故答案为美元.
15.【答案】②③
【解析】①在线性回归模型中,相关指数表示解释变量对于预报变量的贡献率,越接近于1,表示回归效果越好,所以①错误;
②在回归直线方程中,当解释变量x每增加一个单位时,预报变量平均增加个单位,正确;
③两个变量相关性越强,则相关系数的绝对值就越接近于1,正确;
④对分类变量X与Y,对它们的随机变量的观测值k来说,k越小,则“X与Y有关系”的把握程度越小,所以④错误,
故正确命题的序号是②③.
16.【答案】
【解析】由,得,
,
当时,,所以年销售量.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1);(2)该线性回归方程的拟合效果是良好,理由见解析.
【解析】(1)∵,,
将代入回归方程得,∴.
(2),
y关于x的线性回归方程为,
∴,
,
∴,
故该线性回归方程的拟合效果是良好.
18.【答案】(1)列联表见解析,没有;(2)分布列见解析,.
【解析】(1)列联表补充如下:
男生
女生
合计
喜欢抖音上课
10
6
16
不喜欢抖音上课
6
8
14
合计
16
14
30
由30人中随机抽取1人抽到喜欢抖音上课的学生的概率是,
故喜欢抖音上课的学生共有16人.
由已知数据可求得,
所以没有95%的把握认为喜欢抖音上课与性别有关.
(2)X的可能取值为0,1,2.
,,,
所以X的分布列为:
X
0
1
2
P
X的数学期望为.
19.【答案】(1),估计该班某同学的数学成绩为90分时该同学的物理成绩为63分;(2)能在犯错误的概率不超过的前提下认为数学优秀与物理优秀有关.
【解析】(1),
,
,
,
关于的线性回归方程为,
取,得,
估计该班某同学的数学成绩为90分时该同学的物理成绩为63分.
(2)由题意填写列联表:
物理优秀
物理不优秀
合计
数学优秀
24
6
30
数学不优秀
12
18
30
合计
36
24
60
,
能在犯错误的概率不超过的前提下认为数学优秀与物理优秀有关.
20.【答案】(1);(2)食堂购买袋食,能获得最大利润,最大利润为元.
【解析】(1)由所给数据可得,,
,,
故关于的线性回归方程为.
(2)因为,所以当时,,即预计需要购买食材袋,
因为,
所以当时,利润,
此时当时,,
当时,由题意可知,剩余的食材只能无偿退还,
此时当时,,
当时,利润,
综上所述,食堂应购买袋食,才能获得最大利润,最大利润为元.
21.【答案】(1)模型二拟合效果好;(2)(i)2020年4月份二手房均价的预测值为(万元平方米);(ii)最大面积为94平方米.
【解析】(1)模型一中,的残差平方和为,
相关指数为;
模型二中,的残差平方和为,
相关指数为,
相关指数较大的模型二拟合效果好些.
(2)通过散点图确定2020年4月对应的,
代入(1)中拟合效果更好的模型二,代入计算
(万元平方米),
则2020年4月份二手房均价的预测值为(万元平方米),
(i)设该购房者应支付的购房金额万元,因为税费中买方只需缴纳契税,
①当时,契税为计税价格的,
故;
②当时,契税为计税价格的,
故;
③当时,契税为计税价格的,
故,
,
当时购房金额为万元,
当时购房金额为万元,
当时购房金额为万元.
(ii)设该购房者可购买该小区二手房的最大面积为平方米,
由(i)知,当时,应支付的购房金额为,
又;
又因为房屋均价约为万元平方米,所以,所以,
由,解得,且,
所以该购房者可购买该小区二手房的最大面积为94平方米.
22.【答案】(1),;(2)方案1更适合,万亿元.
【解析】(1),
,
,,
,,
关于的回归方程为,
由,
.
(2)由(1)知,,
更适合作为全国进出口贸易总额关于的回归方程,
2020年对应的,当时,,
可以预测2020年全国进出口贸易总额为万亿元.
班级 姓名 准考证号 考场号 座位号
此卷只装订不密封
班级 姓名 准考证号 考场号 座位号
2021学年度高中数学选修2-3第三章统计案例双基精品试卷
统计案例(B)
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是( )
A. B.
C. D.
2.为了解学生对街舞的喜欢是否与性别有关,在全校学生中进行抽样调查,根据数据,求得的观测值,则至少有( )的把握认为对街舞的喜欢与性别有关.参考数据:
A. B. C. D.
3.为检测某药品服用后的多长时间开始有药物反应,现随机抽取服用了该药品的1000人,其服用后开始有药物反应的时间(分钟)与人数的数据绘成的频率分布直方图如图所示.若将直方图中分组区间的中点值设为解释变量(分钟),这个区间上的人数为(人),易见两变量,线性相关,那么一定在其线性回归直线上的点为( )
A. B. C. D.
4.2015年年岁史诗大剧《芈月传》风靡大江南北,影响力不亚于以前的《甄嬛传》.某记者调查了大量《芈月传》的观众,发现年龄段与爱看的比例存在较好的线性相关关系,年龄在,,,,的爱看比例分别为,,,,.现用这5个年龄段的中间值代表年龄段,如12代表,代表,根据前四个数据求得关于爱看比例的线性回归方程为,由此可推测的值为( )
A. B. C. D.
5.某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系,随机抽查52名中学生,得到统计数据如表1至表4,这与性别有关联的可能性最大的变量是( )
A.成绩 B.视力 C.智商 D.阅读量
6.为预测某种产品的回收率y,需要研究它和原料有效成分的含量x之间的相关关系,现取了8组观察值.计算得,,,,则y对x的回归方程是( )
A. B.
C. D.
7.某饮料店的日销售收入(单位:百元)与当天平均气温(单位:)之间有下列数据:
0
1
2
4
2
2
1
甲、乙、丙三位同学对上述数据进行研究,分别得到了与之间的四个线性回归方程,其中正确的是( )
A. B.
C. D.
8.变量与相对应的一组数据为,,,,;变量与相对应的一组数据为,,,,.表示变量,之间的线性相关系数,表示变量与之间的线性相关系数,则( )
A. B. C. D.
9.某商场为了了解不同厂家生产的散装面包的月销售量(千克)与售价(元/千克)之间的关系,随机统计了某几个月的月销售量与当月各散装面包的售价,相关数据如下表:
售价(元/千克)
月销售量(千克)
由表中数据算出线性回归方程为,则样本在处的残差为( )
A. B. C. D.
10.下列有关线性回归分析的六个命题:
①线性回归直线必过样本数据的中心点;
②回归直线就是散点图中经过样本数据点最多的那条直线;
③当相关性系数时,两个变量正相关;
④如果两个变量的相关性越强,则相关性系数就越接近于1;
⑤残差图中残差点所在的水平带状区域越宽,则回归方程的预报精确度越高;
⑥甲、乙两个模型的分别约为和,则模型乙的拟合效果更好.
其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
11.假设2个分类变量X和Y的2×2列联表如下:
Y
X
y1
y2
总计
x1
a
10
a+10
x2
c
30
c+30
总计
a+c
40
100
对于同一样本,以下数据能说明和有关系的可能性最大的一组是( )
A., B.,
C., D.,
12.下列四个命题:
①在回归模型中,预报变量y的值不能由解释变量x唯一确定;
②若变量x,y满足关系,且变量y与z正相关,则x与z也正相关;
③在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;
④以模型去拟合一组数据时,为了求出回归方程,设,将其变换后得到线性方程,则,.
其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题:本大题共4小题,每小题5分.
13.已知x、y之间的一组数据如下:
x
0
1
2
3
y
8
2
6
4
则线性回归方程所表示的直线必经过点________.
14.如图所示是世界20个地区受教育程度的人口百分比与人均收入的散点图,样本点基本集中在一个条型区域,因此两个变量呈线性相关关系.利用散点图中的数据建立的回归方程为,若受教育的人口百分比相差10%,则其人均收入相差_________.
15.已知如下四个命题:①在线性回归模型中,相关指数表示解释变量对于预报变量的贡献率,越接近于,表示回归效果越好;②在回归直线方程中,当解释变量每增加一个单位时,预报变量平均增加个单位;③两个变量相关性越强,则相关系数的绝对值就越接近于;④对分类变量与,对它们的随机变量的观测值来说,越小,则“与有关系”的把握程度越大.其中正确命题的序号是__________.
16.某汽车销售公司为确定下一年度投入某种产品的宣传费,需了解年宣传费(单位:千元)对年销售量(单位:百辆)的影响,对近8年的年宣传费和年销售量数据作了初步处理,得到年销售量与年宣传费具有近似关系:以及一些统计量的值如下:,,,.
已经求得近似关系中的系数,请你根据相关回归分析方法预测当年宣传费(千元)时,年销售量__________(百辆).
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)某机构为了解某大学中男生的体重单位:)与身高x(单位:)是否存在较好的线性关系,该机构搜集了7位该校男生的数据,得到如下表格:
序号
1
2
3
4
5
6
7
身高()
161
175
169
178
173
168
180
体重()
52
62
54
70
66
57
73
根据表中数据计算得到关于的线性回归方程为.
(1)求;
(2)已知且当时,回归方程的拟合效果非常好;当时,回归方程的拟合效果良好.试问该线性回归方程的拟合效果是非常好还是良好?说明你的理由.参考数据:.
18.(12分)今年疫情期间,许多老师进行抖音直播上课某校团委为了解学生喜欢抖音上课是否与性别有关,从高三年级中随机抽取30名学生进行了问卷调查,得到如下列联表:
男生
女生
合计
喜欢抖音上课
10
不喜欢抖音上课
8
合计
30
已知在这30人中随机抽取1人抽到喜欢抖音上课的学生的概率是.
(1)请将上面的列联表补充完整,并据此资料分析能否有95%的把握认为喜欢抖音上课与性别有关?
(2)若从这30人中的女生中随机抽取2人,记喜欢抖音上课的人数为X,求X的分布列、数学期望.
附临界值表:
参考公式:,其中.
19.(12分)高二理科班有60名同学参加某次考试,从中随机抽选出5名同学,他们的数学成绩与物理成绩如下表:
数学成绩
140
130
120
110
100
物理成绩
110
90
100
80
70
数据表明与之间有较强的线性关系.
(1)求关于的线性回归方程,并估计该班某同学的数学成绩为90分时该同学的物理成绩;
(2)本次考试中,规定数学成绩达到125分为数学优秀,物理成绩达到100分为物理优秀.若该班数学优秀率与物理优秀率分别为50%和60%,且所有同学中数学优秀但物理不优秀的同学共有6人,请你在答卷页上填写下面列联表,并判断能否在犯错误的概率不超过的前提下认为数学优秀与物理优秀有关?
物理优秀
物理不优秀
合计
数学优秀
数学不优秀
合计
参考公式及数据:回归直线的系数,,,,,,.
20.(12分)学校食堂统计了最近天到餐厅就餐的人数(百人)与食堂向食材公司购买所需食材(原材料)的数量(袋),得到如下统计表:
第一天
第二天
第三天
第四天
第五天
就餐人数(百人)
13
9
8
10
12
原材料(袋)
32
23
18
24
28
(1)根据所给的组数据,求出关于的线性回归方程;
(2)已知购买食材的费用(元)与数量(袋)的关系为,投入使用的每袋食材相应的销售单价为元,多余的食材必须无偿退还食材公司,据悉下周一大约有人到食堂餐厅就餐,根据(1)中求出的线性回归方程,预测食堂应购买多少袋食材,才能获得最大利润,最大利润是多少?(注:利润L =销售收入-原材料费用)
参考公式:,,
参考数据:,,.
21.(12分)2019年的“金九银十”变成“铜九铁十”,国各地房价“跳水”严重,但某地二手房交易却“逆市”而行.如图是该地某小区2018年11月至2019年1月间,当月在售二手房均价(单位:万元平方米)的散点图.(图中月份代码1~13分别对应2018年11月~2019年11月)
根据散点图选择和两个模型进行拟合,经过数据处理得到两个回归方程分别为和,并得到以下一些统计量的值:
(1)请利用相关指数判断哪个模型的拟合效果更好;
(2)某位购房者拟于2020年4月购买这个小区平方米的二手房(欲购房为其家庭首套房).
若购房时该小区所有住房的房产证均已满2但未满5年,请你利用(1)中拟合效果更好的模型解决以下问题:
(i)估算该购房者应支付的购房金额;(购房金额房款税费,房屋均价精确到万元平方米);
(ii)若该购房者拟用不超过100万元的资金购买该小区一套二手房,试估算其可购买的最大面积.(精确到1平方米)
附注:根据有关规定,二手房交易需要缴纳若干项税费,税费是按房屋的计税价格(计税价格房款)进行征收的.
房产证满2年但未满5年的征收方式如下:首套面积90平方米以内(含90平方米)为;首套面积90平方米以上且140平方米以内(含140平方米);首套面积140平方米以上或非首套为.
参考数据:,,,,,,,.
参考公式:相关指数.
22.(12分)根据国家统计局数据,1999年至2019年我国进出口贸易总额从3万亿元跃升至万亿元,中国在国际市场上的贸易份额越来越大对外贸易在国民经济中的作用日益突出.将年份1999,2004,2009,2014,2019分别用1,2,3,4,5代替,并表示为,表示全国进出口贸易总额.
(1)根据以上统计数据及图表,给出了下列两个方案,请解决方案1中的问题.
方案1:用作为全国进出口贸易总额关于的回归方程,根据以下参考数据,求出关于的回归方程,并求相关指数.
方案2:用作为全国进出口贸易总额关于的回归方程,求得回归方程,相关指数.
(2)通过对比(1)中两个方案的相关指数,你认为哪个方案中的回归方程更合适,并利用此回归方程预测2020年全国进出口贸易总额.
参考数据:
①;②;③;④.
参考公式:线性回归方程中的斜率和截距的最小二乘法估计公式分别为:,,相关指数.
统计案例(B)答 案
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】A
【解析】因为商品销售量与销售价格负相关,所以排除B,D选项,
将代入,可得,不符合实际,故A正确.
2.【答案】B
【解析】因为,所以有的把握认为对街舞的喜欢与性别有关.
3.【答案】C
【解析】由频率分布直方图可知,第一个区间中点坐标,,
第二个区间中点坐标,,
第三个区间中点坐标,,
第四个区间中点坐标,,
则,,
则一定在其线性回归直线上的点为,故选C.
4.【答案】B
【解析】前4个数据对应的,(把百分数转化为小数),
而,
,,,
当,.
5.【答案】D
【解析】由表中数据可得
表1:;
表2:;
表3:;
表4:.
其中最大,所以阅读量与性别有关联的可能性最大,故D正确.
6.【答案】A
【解析】由,,直接计算得,,
所以,选A.
7.【答案】A
【解析】由题意可知,,
由回归方程过中心点,代入选项中只有A项满足.
8.【答案】C
【解析】变量与相对应的一组数据为,,,,,
,,
即;
变量与相对应的一组数据为,,,,,
,
这一组数据的相关系数,
则第一组数据的相关系数大于,第二组数据的相关系数小于,
则,故选C.
9.【答案】B
【解析】由表格得为,
又回归直线方程经过样本中心点,
所以,解得,
所以回归直线方程为,
把代入回归直线方程可得,
故样本在处的残差为,故选B.
10.【答案】B
【解析】①线性回归直线必过样本数据中心点,故①正确;
②回归直线方程在散点图中可能不经过任意样本数据点,故②错误;
③当相关性系数时,则两个变量正相关,故③正确;
④如果两个变量的相关性越强,则相关性系数就越接近于1或,故④错误;
⑤残差图中残差点所在的水平带状区域越窄,回归方程的预报精确度越高,
故⑤错误;
⑥甲、乙两个模型的分别约为和,则模型甲的拟合效果更好,
故⑥错误,
真命题的个数为,故选B.
11.【答案】B
【解析】的观测值,
根据2×2列联表和独立性检验的相关知识,当,一定时,,相差越大,
与相差就越大,就越大,即和有关系的可能性越大,
选项B中,与其它选项相比相差最大,故选B.
12.【答案】C
【解析】下列四个命题:
①在回归模型中,预报变量y的值不能由解释变量x唯一确定;根据回归模型中的变量关系,正确;
②若变量x,y满足关系,且变量y与z正相关,则x与z也正相关;应该是负相关,故错误;
③在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高,即越接近于回归直线的距离越小,故正确;
④以模型去拟合一组数据时,为了求出回归方程,设,将其变换后得到线性方程,则,,故正确,
故选C.
二、填空题:本大题共4小题,每小题5分.
13.【答案】
【解析】由题意可得,,
线性回归方程过样本中心点,即线性回归方程所表示的直线必经过点.
14.【答案】美元
【解析】设所受教育百分比分别为,,且,
根据回归方程为,
收入相差大约为,
即受教育的人口百分比相差,则其人均收入相差约美元,
故答案为美元.
15.【答案】②③
【解析】①在线性回归模型中,相关指数表示解释变量对于预报变量的贡献率,越接近于1,表示回归效果越好,所以①错误;
②在回归直线方程中,当解释变量x每增加一个单位时,预报变量平均增加个单位,正确;
③两个变量相关性越强,则相关系数的绝对值就越接近于1,正确;
④对分类变量X与Y,对它们的随机变量的观测值k来说,k越小,则“X与Y有关系”的把握程度越小,所以④错误,
故正确命题的序号是②③.
16.【答案】
【解析】由,得,
,
当时,,所以年销售量.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1);(2)该线性回归方程的拟合效果是良好,理由见解析.
【解析】(1)∵,,
将代入回归方程得,∴.
(2),
y关于x的线性回归方程为,
∴,
,
∴,
故该线性回归方程的拟合效果是良好.
18.【答案】(1)列联表见解析,没有;(2)分布列见解析,.
【解析】(1)列联表补充如下:
男生
女生
合计
喜欢抖音上课
10
6
16
不喜欢抖音上课
6
8
14
合计
16
14
30
由30人中随机抽取1人抽到喜欢抖音上课的学生的概率是,
故喜欢抖音上课的学生共有16人.
由已知数据可求得,
所以没有95%的把握认为喜欢抖音上课与性别有关.
(2)X的可能取值为0,1,2.
,,,
所以X的分布列为:
X
0
1
2
P
X的数学期望为.
19.【答案】(1),估计该班某同学的数学成绩为90分时该同学的物理成绩为63分;(2)能在犯错误的概率不超过的前提下认为数学优秀与物理优秀有关.
【解析】(1),
,
,
,
关于的线性回归方程为,
取,得,
估计该班某同学的数学成绩为90分时该同学的物理成绩为63分.
(2)由题意填写列联表:
物理优秀
物理不优秀
合计
数学优秀
24
6
30
数学不优秀
12
18
30
合计
36
24
60
,
能在犯错误的概率不超过的前提下认为数学优秀与物理优秀有关.
20.【答案】(1);(2)食堂购买袋食,能获得最大利润,最大利润为元.
【解析】(1)由所给数据可得,,
,,
故关于的线性回归方程为.
(2)因为,所以当时,,即预计需要购买食材袋,
因为,
所以当时,利润,
此时当时,,
当时,由题意可知,剩余的食材只能无偿退还,
此时当时,,
当时,利润,
综上所述,食堂应购买袋食,才能获得最大利润,最大利润为元.
21.【答案】(1)模型二拟合效果好;(2)(i)2020年4月份二手房均价的预测值为(万元平方米);(ii)最大面积为94平方米.
【解析】(1)模型一中,的残差平方和为,
相关指数为;
模型二中,的残差平方和为,
相关指数为,
相关指数较大的模型二拟合效果好些.
(2)通过散点图确定2020年4月对应的,
代入(1)中拟合效果更好的模型二,代入计算
(万元平方米),
则2020年4月份二手房均价的预测值为(万元平方米),
(i)设该购房者应支付的购房金额万元,因为税费中买方只需缴纳契税,
①当时,契税为计税价格的,
故;
②当时,契税为计税价格的,
故;
③当时,契税为计税价格的,
故,
,
当时购房金额为万元,
当时购房金额为万元,
当时购房金额为万元.
(ii)设该购房者可购买该小区二手房的最大面积为平方米,
由(i)知,当时,应支付的购房金额为,
又;
又因为房屋均价约为万元平方米,所以,所以,
由,解得,且,
所以该购房者可购买该小区二手房的最大面积为94平方米.
22.【答案】(1),;(2)方案1更适合,万亿元.
【解析】(1),
,
,,
,,
关于的回归方程为,
由,
.
(2)由(1)知,,
更适合作为全国进出口贸易总额关于的回归方程,
2020年对应的,当时,,
可以预测2020年全国进出口贸易总额为万亿元.
