2021学年度高中数学选修2-3第一章计数原理双基精品试卷 计数原理(A)(含答案)
文档属性
| 名称 | 2021学年度高中数学选修2-3第一章计数原理双基精品试卷 计数原理(A)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 11:57:15 | ||
图片预览



文档简介
-1123950339725此卷只装订不密封
班级 姓名 准考证号 考场号 座位号
此卷只装订不密封
班级 姓名 准考证号 考场号 座位号
2021学年度高中数学选修2-3第一章计数原理双基精品试卷
计数原理(A)
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知下列问题:
①从甲、乙、丙三名同学中选出两名分别参加数学和物理学习小组
②从甲、乙、丙三名同学中选出两名同学参加一项活动
③从a,b,c,d四个字母中取出2个字母
④从1,2,3,4四个数字中取出2个数字组成一个两位数
其中是排列问题的有( )
A.1个 B.2个 C.3个 D.4个
2.在的展开式中,常数项为( )
A. B. C. D.
3.2020年12月1日,大连市开始实行生活垃圾分类管理.某单位有四个垃圾桶,分别是一个可回收物垃圾桶?一个有害垃圾桶?一个厨余垃圾桶?一个其它垃圾桶.因为场地限制,要将这四个垃圾桶摆放在三个固定角落,每个角落至少摆放一个,则不同的摆放方法共有(如果某两个垃圾桶摆放在同一角落,它们的前后左右位置关系不作考虑)( )
A.种 B.种 C.种 D.种
4.在的展开式中,第2项与第6项的二项式系数相等,则( )
A.6 B.7 C.8 D.9
5.已知的展开式中各项系数的和为2,则该展开式中常数项为( )
A. B. C. D.
6.某海军舰长要求队员们依次完成六项任务,并对任务的顺序提出了如下要求:重点任务A必须排在前三位,且任务E?F必须排在一起,则这六项任务的不同安排方案共有( )
A.240种 B.188种 C.156种 D.120种
7.化简:( )
A. B. C. D.
8.第十一届全国少数民族传统体育运动会在河南郑州举行,某项目比赛期间需要安排3名志愿者完成5项工作,每人至少完成一项,每项工作由一人完成,则不同的安排方式共有( )种.
A.60 B.90 C.120 D.150
9.牡丹江一中2019年将实行新课程改革,即除语、数、外三科为必考科目外,还要在理、化、生、史、地、政六科中选择三科作为选考科目.已知某生的高考志愿为北京大学环境科学专业,按照17年北大高考招生选考科目要求物、化必选,为该生安排课表(上午四节、下午四节,上午第四节和下午第一节不算相邻),现该生某天最后两节为自习课,且数学不排下午第一节,语文、外语不相邻,则该生该天课表有( )种.
A.444 B.1776 C.1440 D.1560
10.的所有可能的值是( )
A.7 B.4或7
C.7或11 D.4或7或11
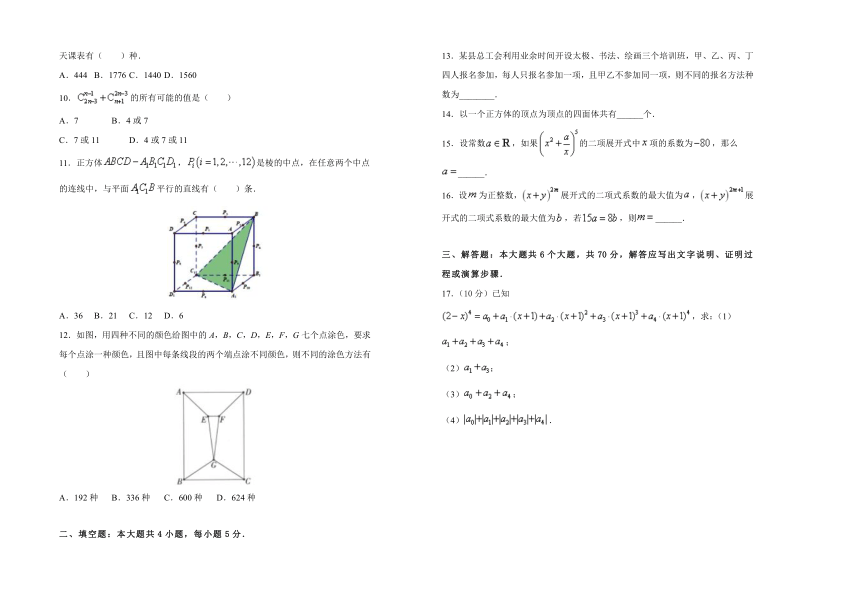
11.正方体,是棱的中点,在任意两个中点的连线中,与平面平行的直线有( )条.
A.36 B.21 C.12 D.6
12.如图,用四种不同的颜色给图中的A,B,C,D,E,F,G七个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法有( )
A.192种 B.336种 C.600种 D.624种
二、填空题:本大题共4小题,每小题5分.
13.某县总工会利用业余时间开设太极、书法、绘画三个培训班,甲、乙、丙、丁四人报名参加,每人只报名参加一项,且甲乙不参加同一项,则不同的报名方法种数为________.
14.以一个正方体的顶点为顶点的四面体共有______个.
15.设常数,如果的二项展开式中项的系数为,那么______.
16.设为正整数,展开式的二项式系数的最大值为,展开式的二项式系数的最大值为,若,则______.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知,求:(1);
(2);
(3);
(4).
18.(12分)名班委有种不同的职务,甲、乙、丙三人在名班委中,现对名班委进行职务具体分工.
(1)若正、副班长两职只能从甲、乙、丙三人中选两人担任,有多少种不同的分工方案?
(2)若正、副班长两职至少要选甲、乙、丙三人中的一人担任,有多少种不同的分工方案?
19.(12分)一条铁路有个车站,为适应客运需要,新增了个车站,且知,客运车票增加了62种,问原来有多少个车站?现在有多少个车站?
20.(12分)一场小型晚会有个唱歌节目和个相声节目,要求排出一个节目单.
(1)个相声节目要排在一起,有多少种排法?
(2)第一个节目和最后一个节目都是唱歌节目,有多少种排法?
(3)前个节目中要有相声节目,有多少种排法?
(要求:每小题都要有过程,且计算结果都用数字表示)
21.(12分)按照下列要求,分别求有多少种不同的方法?(用数字作答)
(1)个不同的小球放入个不同的盒子;
(2)个不同的小球放入个不同的盒子,每个盒子至少一个小球;
(3)个相同的小球放入个不同的盒子,每个盒子至少一个小球;
(4)个不同的小球放入个不同的盒子,恰有个空盒.
22.(12分)从1到9的九个数字中取三个偶数四个奇数,试问:
(1)能组成多少个没有重复数字的七位数?
(2)在(1)中的七位数中三个偶数排在一起的有几个?
(3)在(1)中的七位数中,偶数排在一起、奇数也排在一起的有几个?
(4)在(1)中任意两偶然都不相邻的七位数有几个?
(答题要求:先列式,后计算,结果用具体数字表示.)
计数原理(A)答 案
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】B
【解析】①中,因为两名同学参加的学习小组与顺序有关,所以是排列问题;
②中,因为两名同学参加的活动与顺序无关,不是排列问题;
③中,因为取出的两个字母与顺序无关,不是排列问题;
④中,因为取出的两个数字还需要按顺序排列,是排列问题,
故选B.
2.【答案】B
【解析】二项式展开式的通项为,
令,解得,所以,故选B.
3.【答案】C
【解析】根据题意,有四个垃圾桶放到三个固定角落,其中有一个角落放两个垃圾桶,
先选出两个垃圾桶,有种选法,
之后与另两个垃圾桶分别放在三个不同的地方有种放法,
所以不同的摆放方法共有种,故选C.
4.【答案】A
【解析】由已知得,可知,故选A.
5.【答案】D
【解析】令二项式中的为1得到展开式的各项系数和为,
,,
,
展开式中常数项为的常数项与含的系数和,
展开式的通项为,
令,得;令,无整数解,
展开式中常数项为,故选D.
6.【答案】D
【解析】当E,F排在前三位时,有种安排方案;
当E,F排在后三位时,有种安排方案:
当E,F排中间两位时,有种安排方案,
综上,不同的安排方案共有(种),故选D.
7.【答案】B
【解析】,
故选B.
8.【答案】D
【解析】根据题意,分2步进行分析:
①、将5项工作分成3组,
若分成1、1、3的三组,有种分组方法,
若分成1、2、2的三组,有种分组方法,
则将5项工作分成3组,有种分组方法;
②、将分好的三组全排列,对应3名志愿者,有种情况,
则有种不同的分组方法,故选D.
9.【答案】B
【解析】首先理、化、生、史、地、政六选三,且物、化必选,
所以只需在生、史、地、政四选一有种;
然后对语文、外语排课进行分类,
第1类:语文外语有一科在下午第一节,则另一科可以安排在上午四节课任意一节,剩下的四科可全排列,共种;
第2类:语文外语都不在下午第一节,则下午第一节可在除语数外三科的另三科中选择,语文和外语可都安排在上午,可以是上午第一、三,上午一、四、上午二、四节3种,也可一科在上午任一节一科在下午第二节,其他三科可以全排列,共,
所以总共有种.
10.【答案】D
【解析】由组合数的条件可知,即,故n=2,3,4.
当时,;
当时,;
当时,,
故选D.
11.【答案】B
【解析】考虑与平面平行的平面,平面,平面,
共有,故选B.
12.【答案】C
【解析】由题意,点E,F,G分别有4,3,2种涂法,
(1)当A与F相同时,A有1种涂色方法,此时B有2种涂色方法,
①若C与F相同,则C有1种涂色方法,此时D有3种涂色方法;
②若C与F不同,则D有2种涂色方法.
故此时共有种涂色方法;
(2)当A与G相同时,A有1种涂色方法,
①若C与F相同,则C有1种涂色方法,此时B有2种涂色方法,D有2种涂色方法;
②若C与F不同,则C有2种涂色方法,此时B有2种涂色方法,D有1种涂色方法.
故此时共有种涂色方法;
(3)当A既不同于F又不同于G时,A有1种涂色方法.
①若B与F相同,则C与A相同时,D有2种涂色方法,C与A不同时,C和D均只有1种涂色方法;
②若B与F不同,则B有1种涂色方法,
(i)若C与F相同,则C有1种涂色方法,此时D有2种涂色方法;
(ii)若C与F不同,则必与A相同,C有1种涂色方法,此时D有2种涂色方法,
故此时共有种涂色方法,
综上,共有种涂色方法,故选C.
二、填空题:本大题共4小题,每小题5分.
13.【答案】54
【解析】甲有三个培训可选,甲乙不参加同一项,所以乙有二个培训可选,丙、丁各有三个培训可选,
根据乘法计数原理,不同的报名方法种数为.
14.【答案】
【解析】正方体的个顶点中任取个共有个,
不能组成四面体的个顶点有,已有个面,对角面有个,
所以,以一个正方体的顶点为顶点的四面体共有个,
故答案为.
15.【答案】
【解析】的二项展开式的通项公式,
令,解得,
∴,解得,
故答案为.
16.【答案】7
【解析】展开式中二项式系数的最大值为,
展开式中二项式系数的最大值为,
因为,所以,
即,解得.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1);(2);(3);(4).
【解析】令,则①,
令,则②,
令,则③,
(1)②-①,得.
(2)(②-③),得.
(3)(②+③),得.
(4).
18.【答案】(1)种;(2)种.
【解析】(1)先排正、副班长,有种方法,再安排其余职务有种方法,
由分步乘法计数原理知共有种不同的分工方案.
(2)人中任意分工,有种不同的分工方案,
甲、乙、丙三人中无一人担任正、副班长的分工方案有种,
因此甲、乙、丙三人中至少有一人担任正、副班长的分工方案有种.
19.【答案】15;17.
【解析】原来个车站有车票种,新增了个车站,有车票种,
由题意得,即,
整理得,∴,
由从而有,∴.
又∵,解得,即,
当时,均不为整数,只有时,符合题意,
∴,故原来有15个车站,现在有17个车站.
20.【答案】(1);(2);(3).
【解析】(1)把两个相声节目捆绑在一起作为一个节目与其他节目排列共有排法.
(2)选两个唱歌节目排在首尾,剩下的3个节目在中间排列,排法为.
(3)5个节目全排列减去后两个都是相声的排法,共有.
21.【答案】(1)4096;(2)1560;(3)10;(4)2160.
【解析】(1).
(2).
(3)或.
(4).
22.【答案】(1)100800个;(2)14400个;(3)5760个;(4)28800个.
【解析】(1)分步完成:第一步在四个偶数中取三个,可有种情况;
第二步在五个奇数中取四个,可有种情况;
第三步三个偶数,四个奇数进行排列,可有种情况,
所以符合题意的七位数有个.
(2)上述七位数中,三个偶数排在一起的有.
(3)上述七位数中,三个偶数排在一起,四个奇数也排在一起的有个.
(4)上述七位数中,偶数都不相邻,可先把四个奇数排好,再将三个偶数分别插入5个空档,
共有个.
班级 姓名 准考证号 考场号 座位号
此卷只装订不密封
班级 姓名 准考证号 考场号 座位号
2021学年度高中数学选修2-3第一章计数原理双基精品试卷
计数原理(A)
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知下列问题:
①从甲、乙、丙三名同学中选出两名分别参加数学和物理学习小组
②从甲、乙、丙三名同学中选出两名同学参加一项活动
③从a,b,c,d四个字母中取出2个字母
④从1,2,3,4四个数字中取出2个数字组成一个两位数
其中是排列问题的有( )
A.1个 B.2个 C.3个 D.4个
2.在的展开式中,常数项为( )
A. B. C. D.
3.2020年12月1日,大连市开始实行生活垃圾分类管理.某单位有四个垃圾桶,分别是一个可回收物垃圾桶?一个有害垃圾桶?一个厨余垃圾桶?一个其它垃圾桶.因为场地限制,要将这四个垃圾桶摆放在三个固定角落,每个角落至少摆放一个,则不同的摆放方法共有(如果某两个垃圾桶摆放在同一角落,它们的前后左右位置关系不作考虑)( )
A.种 B.种 C.种 D.种
4.在的展开式中,第2项与第6项的二项式系数相等,则( )
A.6 B.7 C.8 D.9
5.已知的展开式中各项系数的和为2,则该展开式中常数项为( )
A. B. C. D.
6.某海军舰长要求队员们依次完成六项任务,并对任务的顺序提出了如下要求:重点任务A必须排在前三位,且任务E?F必须排在一起,则这六项任务的不同安排方案共有( )
A.240种 B.188种 C.156种 D.120种
7.化简:( )
A. B. C. D.
8.第十一届全国少数民族传统体育运动会在河南郑州举行,某项目比赛期间需要安排3名志愿者完成5项工作,每人至少完成一项,每项工作由一人完成,则不同的安排方式共有( )种.
A.60 B.90 C.120 D.150
9.牡丹江一中2019年将实行新课程改革,即除语、数、外三科为必考科目外,还要在理、化、生、史、地、政六科中选择三科作为选考科目.已知某生的高考志愿为北京大学环境科学专业,按照17年北大高考招生选考科目要求物、化必选,为该生安排课表(上午四节、下午四节,上午第四节和下午第一节不算相邻),现该生某天最后两节为自习课,且数学不排下午第一节,语文、外语不相邻,则该生该天课表有( )种.
A.444 B.1776 C.1440 D.1560
10.的所有可能的值是( )
A.7 B.4或7
C.7或11 D.4或7或11
11.正方体,是棱的中点,在任意两个中点的连线中,与平面平行的直线有( )条.
A.36 B.21 C.12 D.6
12.如图,用四种不同的颜色给图中的A,B,C,D,E,F,G七个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法有( )
A.192种 B.336种 C.600种 D.624种
二、填空题:本大题共4小题,每小题5分.
13.某县总工会利用业余时间开设太极、书法、绘画三个培训班,甲、乙、丙、丁四人报名参加,每人只报名参加一项,且甲乙不参加同一项,则不同的报名方法种数为________.
14.以一个正方体的顶点为顶点的四面体共有______个.
15.设常数,如果的二项展开式中项的系数为,那么______.
16.设为正整数,展开式的二项式系数的最大值为,展开式的二项式系数的最大值为,若,则______.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知,求:(1);
(2);
(3);
(4).
18.(12分)名班委有种不同的职务,甲、乙、丙三人在名班委中,现对名班委进行职务具体分工.
(1)若正、副班长两职只能从甲、乙、丙三人中选两人担任,有多少种不同的分工方案?
(2)若正、副班长两职至少要选甲、乙、丙三人中的一人担任,有多少种不同的分工方案?
19.(12分)一条铁路有个车站,为适应客运需要,新增了个车站,且知,客运车票增加了62种,问原来有多少个车站?现在有多少个车站?
20.(12分)一场小型晚会有个唱歌节目和个相声节目,要求排出一个节目单.
(1)个相声节目要排在一起,有多少种排法?
(2)第一个节目和最后一个节目都是唱歌节目,有多少种排法?
(3)前个节目中要有相声节目,有多少种排法?
(要求:每小题都要有过程,且计算结果都用数字表示)
21.(12分)按照下列要求,分别求有多少种不同的方法?(用数字作答)
(1)个不同的小球放入个不同的盒子;
(2)个不同的小球放入个不同的盒子,每个盒子至少一个小球;
(3)个相同的小球放入个不同的盒子,每个盒子至少一个小球;
(4)个不同的小球放入个不同的盒子,恰有个空盒.
22.(12分)从1到9的九个数字中取三个偶数四个奇数,试问:
(1)能组成多少个没有重复数字的七位数?
(2)在(1)中的七位数中三个偶数排在一起的有几个?
(3)在(1)中的七位数中,偶数排在一起、奇数也排在一起的有几个?
(4)在(1)中任意两偶然都不相邻的七位数有几个?
(答题要求:先列式,后计算,结果用具体数字表示.)
计数原理(A)答 案
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】B
【解析】①中,因为两名同学参加的学习小组与顺序有关,所以是排列问题;
②中,因为两名同学参加的活动与顺序无关,不是排列问题;
③中,因为取出的两个字母与顺序无关,不是排列问题;
④中,因为取出的两个数字还需要按顺序排列,是排列问题,
故选B.
2.【答案】B
【解析】二项式展开式的通项为,
令,解得,所以,故选B.
3.【答案】C
【解析】根据题意,有四个垃圾桶放到三个固定角落,其中有一个角落放两个垃圾桶,
先选出两个垃圾桶,有种选法,
之后与另两个垃圾桶分别放在三个不同的地方有种放法,
所以不同的摆放方法共有种,故选C.
4.【答案】A
【解析】由已知得,可知,故选A.
5.【答案】D
【解析】令二项式中的为1得到展开式的各项系数和为,
,,
,
展开式中常数项为的常数项与含的系数和,
展开式的通项为,
令,得;令,无整数解,
展开式中常数项为,故选D.
6.【答案】D
【解析】当E,F排在前三位时,有种安排方案;
当E,F排在后三位时,有种安排方案:
当E,F排中间两位时,有种安排方案,
综上,不同的安排方案共有(种),故选D.
7.【答案】B
【解析】,
故选B.
8.【答案】D
【解析】根据题意,分2步进行分析:
①、将5项工作分成3组,
若分成1、1、3的三组,有种分组方法,
若分成1、2、2的三组,有种分组方法,
则将5项工作分成3组,有种分组方法;
②、将分好的三组全排列,对应3名志愿者,有种情况,
则有种不同的分组方法,故选D.
9.【答案】B
【解析】首先理、化、生、史、地、政六选三,且物、化必选,
所以只需在生、史、地、政四选一有种;
然后对语文、外语排课进行分类,
第1类:语文外语有一科在下午第一节,则另一科可以安排在上午四节课任意一节,剩下的四科可全排列,共种;
第2类:语文外语都不在下午第一节,则下午第一节可在除语数外三科的另三科中选择,语文和外语可都安排在上午,可以是上午第一、三,上午一、四、上午二、四节3种,也可一科在上午任一节一科在下午第二节,其他三科可以全排列,共,
所以总共有种.
10.【答案】D
【解析】由组合数的条件可知,即,故n=2,3,4.
当时,;
当时,;
当时,,
故选D.
11.【答案】B
【解析】考虑与平面平行的平面,平面,平面,
共有,故选B.
12.【答案】C
【解析】由题意,点E,F,G分别有4,3,2种涂法,
(1)当A与F相同时,A有1种涂色方法,此时B有2种涂色方法,
①若C与F相同,则C有1种涂色方法,此时D有3种涂色方法;
②若C与F不同,则D有2种涂色方法.
故此时共有种涂色方法;
(2)当A与G相同时,A有1种涂色方法,
①若C与F相同,则C有1种涂色方法,此时B有2种涂色方法,D有2种涂色方法;
②若C与F不同,则C有2种涂色方法,此时B有2种涂色方法,D有1种涂色方法.
故此时共有种涂色方法;
(3)当A既不同于F又不同于G时,A有1种涂色方法.
①若B与F相同,则C与A相同时,D有2种涂色方法,C与A不同时,C和D均只有1种涂色方法;
②若B与F不同,则B有1种涂色方法,
(i)若C与F相同,则C有1种涂色方法,此时D有2种涂色方法;
(ii)若C与F不同,则必与A相同,C有1种涂色方法,此时D有2种涂色方法,
故此时共有种涂色方法,
综上,共有种涂色方法,故选C.
二、填空题:本大题共4小题,每小题5分.
13.【答案】54
【解析】甲有三个培训可选,甲乙不参加同一项,所以乙有二个培训可选,丙、丁各有三个培训可选,
根据乘法计数原理,不同的报名方法种数为.
14.【答案】
【解析】正方体的个顶点中任取个共有个,
不能组成四面体的个顶点有,已有个面,对角面有个,
所以,以一个正方体的顶点为顶点的四面体共有个,
故答案为.
15.【答案】
【解析】的二项展开式的通项公式,
令,解得,
∴,解得,
故答案为.
16.【答案】7
【解析】展开式中二项式系数的最大值为,
展开式中二项式系数的最大值为,
因为,所以,
即,解得.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1);(2);(3);(4).
【解析】令,则①,
令,则②,
令,则③,
(1)②-①,得.
(2)(②-③),得.
(3)(②+③),得.
(4).
18.【答案】(1)种;(2)种.
【解析】(1)先排正、副班长,有种方法,再安排其余职务有种方法,
由分步乘法计数原理知共有种不同的分工方案.
(2)人中任意分工,有种不同的分工方案,
甲、乙、丙三人中无一人担任正、副班长的分工方案有种,
因此甲、乙、丙三人中至少有一人担任正、副班长的分工方案有种.
19.【答案】15;17.
【解析】原来个车站有车票种,新增了个车站,有车票种,
由题意得,即,
整理得,∴,
由从而有,∴.
又∵,解得,即,
当时,均不为整数,只有时,符合题意,
∴,故原来有15个车站,现在有17个车站.
20.【答案】(1);(2);(3).
【解析】(1)把两个相声节目捆绑在一起作为一个节目与其他节目排列共有排法.
(2)选两个唱歌节目排在首尾,剩下的3个节目在中间排列,排法为.
(3)5个节目全排列减去后两个都是相声的排法,共有.
21.【答案】(1)4096;(2)1560;(3)10;(4)2160.
【解析】(1).
(2).
(3)或.
(4).
22.【答案】(1)100800个;(2)14400个;(3)5760个;(4)28800个.
【解析】(1)分步完成:第一步在四个偶数中取三个,可有种情况;
第二步在五个奇数中取四个,可有种情况;
第三步三个偶数,四个奇数进行排列,可有种情况,
所以符合题意的七位数有个.
(2)上述七位数中,三个偶数排在一起的有.
(3)上述七位数中,三个偶数排在一起,四个奇数也排在一起的有个.
(4)上述七位数中,偶数都不相邻,可先把四个奇数排好,再将三个偶数分别插入5个空档,
共有个.
