5.3绝对值 课件-2020-2021学年沪教版(上海)六年级数学下册(17张PPT)
文档属性
| 名称 | 5.3绝对值 课件-2020-2021学年沪教版(上海)六年级数学下册(17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 818.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 18:55:07 | ||
图片预览



文档简介
第5章 有理数
第1节 有理数
5.3 绝对值
沪教版·六年级数学下册
情景引入
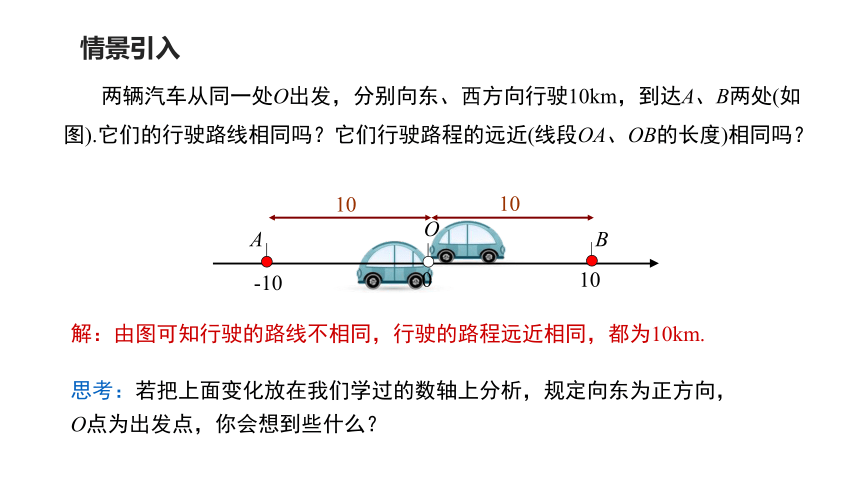
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处(如图).它们的行驶路线相同吗?它们行驶路程的远近(线段OA、OB的长度)相同吗?
A
O
B
10
10
解:由图可知行驶的路线不相同,行驶的路程远近相同,都为10km.
思考:若把上面变化放在我们学过的数轴上分析,规定向东为正方向,O点为出发点,你会想到些什么?
-10
0
10
讨论
什么叫一个数的绝对值?
o
x
b
a
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
│4│=4
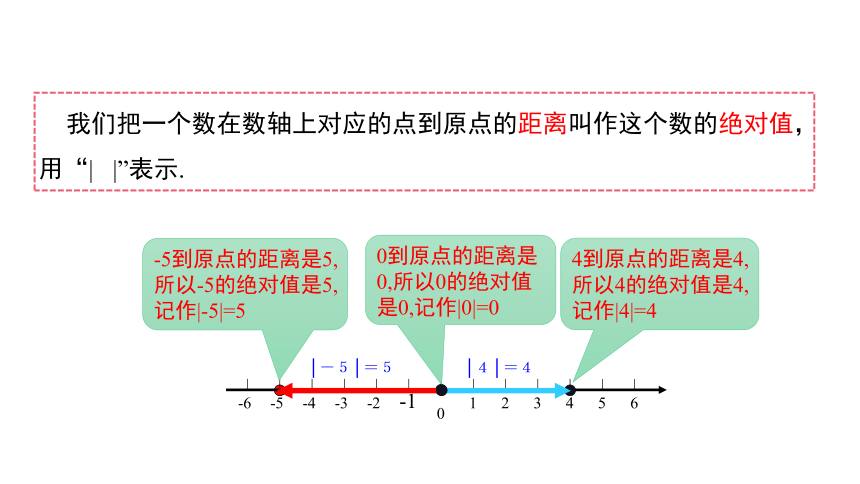
4到原点的距离是4,所以4的绝对值是4,记作|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记作|-5|=5
我们把一个数在数轴上对应的点到原点的距离叫作这个数的绝对值,用“| |”表示.
0到原点的距离是0,所以0的绝对值是0,记作|0|=0
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
4到原点的距离是4,所以4的绝对值是4,记作|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记作|-5|=5
数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.互为相反数的绝对值相等.如-8和8的绝对值是8.
0到原点的距离是0,所以0的绝对值是0,记作|0|=0
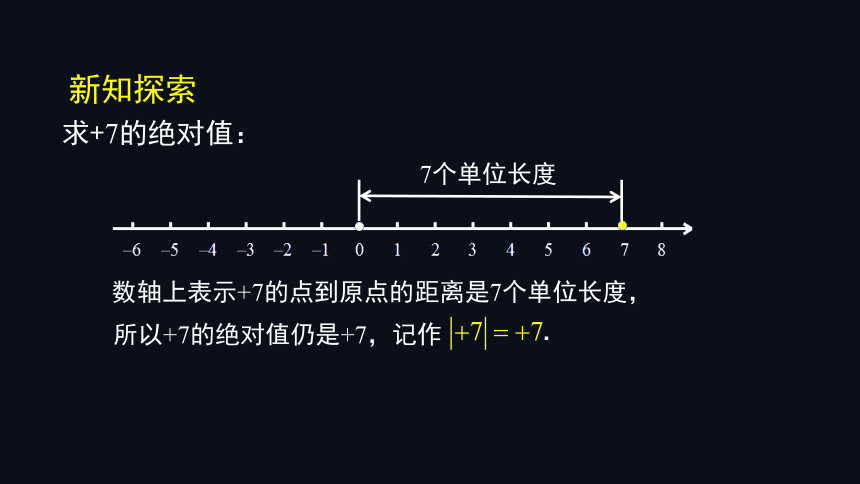
求+7的绝对值:
数轴上表示+7的点到原点的距离是7个单位长度,
所以+7的绝对值仍是+7,记作
新知探索
7个单位长度
判断正误
(1)|-0.3|=|0.3|; ( )
(2)-|-5|=|-5|; ( )
(3)-|3|=|-3|; ( )
(4)有理数的绝对值一定是正数; ( )
(5)绝对值最小的数是0; ( )
(6)如果数a的绝对值等于a,那么a一定为正数 ( )
(7)若a=b,则|a|=|b|; ( )
(8)若|a|=|b|,则a=b. ( )
巩固练习
由绝对值的定义可知:
a.一个正数的绝对值是它本身;
b.一个负数的绝对值是它的相反数;
c.0的绝对值是0.
即
(1)若a > 0,则| a | = a;
(2)若a < 0,则| a | = ﹣a;
(3)若a = 0,则| a | = 0;
讨论下面3个问题:
(1)有没有绝对值等于﹣2的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是什么数?
深入理解
结论:不论有理数a取何值,它的绝对值总是正数或0(非负数),即对任意有理数a,总有|a|≥ 0.
思考
(1)一个数的绝对值会是负数吗?为什么?
(2)不论有理数a取何值,它的绝对值总是什么数?为什么?
重要结论:
任何一个有理数a的绝对值总是非负数
符号表示:|a|≥0
不会是负数!
(3)互为相反数的两个数的绝对值有什么关系?
表示一对相反数的点分别在原点两侧,它们到原点的距离是相等的,所以互为相反数的两个数的绝对值相等。
解:根据题意可知
x-4=0,y-3=0,
所以x=4,y=3,故x+y=7.
归纳总结: 几个非负数的和为0,则这几个数都为0.
[解析] 一个数的绝对值总是大于或等于0,即为非负数,若两个非负数的和为0,则这两个数同时为0.
思考:有理数的大小比较,一定要借助于数轴吗?
能直接进行比较吗?
例.比较下列各数的大小.
解:先化简,-(-3)=3,
-(+2)=-2,
因为正数大于负数,所以3>-2,
即
-(-3)>-(+2)
-(-3)和-(+2);
异号两数比较要考虑它们的正负.
解:两个负数做比较,先求它们的绝对值.
同号两数比较要考虑它们的绝对值.
两负数相比较,绝对值大的反而小.
绝对值
1.数轴上表示数a的点与原点的距离叫做数a的绝对值.
2.绝对值的性质
(1)|a|≥0;
(2)
3.比较有理数大小的方法.
方法①:数轴上表示的两个数,右边的总比左边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
强化练习
(1)一个数的绝对值是4?,则这数是-4. (2)有理数的绝对值一定是正数.
(3)若a=-b,则|a|=|b|.
(4)若|a|=|b|,则a=b.
(5)若|a|=-a,则a必为负数.
(6)互为相反数的两个数的绝对值相等.
判断下列说法是否正确.
×
√
√
×
×
×
判断:
(1)一个数的绝对值是 2?,则这数是2 .
(2)|5|=|-5|.
(3)|-0.3|=|0.3|.
(4)|3|>0.
(5)|-1.4|>0.
(6)有理数的绝对值一定是正数.
(7)若a=b,则|a|=|b|.
(8)若|a|=|b|,则a=b.
(9)若|a|=-a,则a必为负数.
(10)互为相反数的两个数的绝对值相等.
拓展练习
如果a是有理数,试比较|a|与-2a的大小.
分析:由于不能确定a的正负,所以需分类讨论
解:?当a>0时,|a|>0,-2a<0,所以|a|>-2a;
?当a=0时,|a|=0,-2a=0,所以|a|=-2a;
?当a<0时,-2a>0,|a|=-a,
因为-2a>-a,所以|a|<-2a.
第1节 有理数
5.3 绝对值
沪教版·六年级数学下册
情景引入
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处(如图).它们的行驶路线相同吗?它们行驶路程的远近(线段OA、OB的长度)相同吗?
A
O
B
10
10
解:由图可知行驶的路线不相同,行驶的路程远近相同,都为10km.
思考:若把上面变化放在我们学过的数轴上分析,规定向东为正方向,O点为出发点,你会想到些什么?
-10
0
10
讨论
什么叫一个数的绝对值?
o
x
b
a
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
│-5│=5
│4│=4
4到原点的距离是4,所以4的绝对值是4,记作|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记作|-5|=5
我们把一个数在数轴上对应的点到原点的距离叫作这个数的绝对值,用“| |”表示.
0到原点的距离是0,所以0的绝对值是0,记作|0|=0
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
4到原点的距离是4,所以4的绝对值是4,记作|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记作|-5|=5
数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.互为相反数的绝对值相等.如-8和8的绝对值是8.
0到原点的距离是0,所以0的绝对值是0,记作|0|=0
求+7的绝对值:
数轴上表示+7的点到原点的距离是7个单位长度,
所以+7的绝对值仍是+7,记作
新知探索
7个单位长度
判断正误
(1)|-0.3|=|0.3|; ( )
(2)-|-5|=|-5|; ( )
(3)-|3|=|-3|; ( )
(4)有理数的绝对值一定是正数; ( )
(5)绝对值最小的数是0; ( )
(6)如果数a的绝对值等于a,那么a一定为正数 ( )
(7)若a=b,则|a|=|b|; ( )
(8)若|a|=|b|,则a=b. ( )
巩固练习
由绝对值的定义可知:
a.一个正数的绝对值是它本身;
b.一个负数的绝对值是它的相反数;
c.0的绝对值是0.
即
(1)若a > 0,则| a | = a;
(2)若a < 0,则| a | = ﹣a;
(3)若a = 0,则| a | = 0;
讨论下面3个问题:
(1)有没有绝对值等于﹣2的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是什么数?
深入理解
结论:不论有理数a取何值,它的绝对值总是正数或0(非负数),即对任意有理数a,总有|a|≥ 0.
思考
(1)一个数的绝对值会是负数吗?为什么?
(2)不论有理数a取何值,它的绝对值总是什么数?为什么?
重要结论:
任何一个有理数a的绝对值总是非负数
符号表示:|a|≥0
不会是负数!
(3)互为相反数的两个数的绝对值有什么关系?
表示一对相反数的点分别在原点两侧,它们到原点的距离是相等的,所以互为相反数的两个数的绝对值相等。
解:根据题意可知
x-4=0,y-3=0,
所以x=4,y=3,故x+y=7.
归纳总结: 几个非负数的和为0,则这几个数都为0.
[解析] 一个数的绝对值总是大于或等于0,即为非负数,若两个非负数的和为0,则这两个数同时为0.
思考:有理数的大小比较,一定要借助于数轴吗?
能直接进行比较吗?
例.比较下列各数的大小.
解:先化简,-(-3)=3,
-(+2)=-2,
因为正数大于负数,所以3>-2,
即
-(-3)>-(+2)
-(-3)和-(+2);
异号两数比较要考虑它们的正负.
解:两个负数做比较,先求它们的绝对值.
同号两数比较要考虑它们的绝对值.
两负数相比较,绝对值大的反而小.
绝对值
1.数轴上表示数a的点与原点的距离叫做数a的绝对值.
2.绝对值的性质
(1)|a|≥0;
(2)
3.比较有理数大小的方法.
方法①:数轴上表示的两个数,右边的总比左边的大.
方法②:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
强化练习
(1)一个数的绝对值是4?,则这数是-4. (2)有理数的绝对值一定是正数.
(3)若a=-b,则|a|=|b|.
(4)若|a|=|b|,则a=b.
(5)若|a|=-a,则a必为负数.
(6)互为相反数的两个数的绝对值相等.
判断下列说法是否正确.
×
√
√
×
×
×
判断:
(1)一个数的绝对值是 2?,则这数是2 .
(2)|5|=|-5|.
(3)|-0.3|=|0.3|.
(4)|3|>0.
(5)|-1.4|>0.
(6)有理数的绝对值一定是正数.
(7)若a=b,则|a|=|b|.
(8)若|a|=|b|,则a=b.
(9)若|a|=-a,则a必为负数.
(10)互为相反数的两个数的绝对值相等.
拓展练习
如果a是有理数,试比较|a|与-2a的大小.
分析:由于不能确定a的正负,所以需分类讨论
解:?当a>0时,|a|>0,-2a<0,所以|a|>-2a;
?当a=0时,|a|=0,-2a=0,所以|a|=-2a;
?当a<0时,-2a>0,|a|=-a,
因为-2a>-a,所以|a|<-2a.
