五年级下册数学课件 5.1.2 长方体和正方体的体积 冀教版(共74张PPT)
文档属性
| 名称 | 五年级下册数学课件 5.1.2 长方体和正方体的体积 冀教版(共74张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 9.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 22:19:02 | ||
图片预览











文档简介
(共74张PPT)
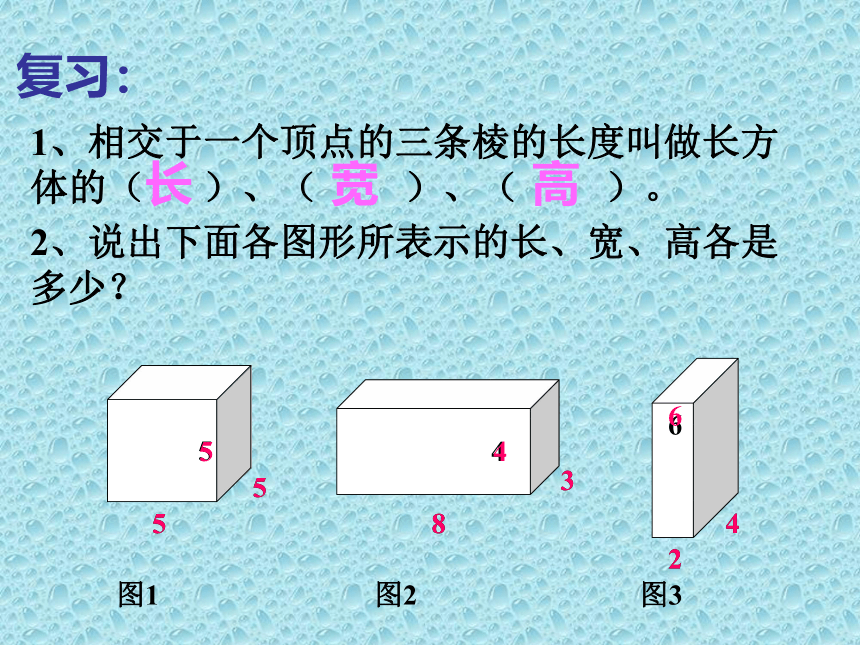
复习:
1、相交于一个顶点的三条棱的长度叫做长方体的(
)、(
)、(
)。
长
高
宽
5
5
5
4
8
3
6
2
4
5
5
5
8
3
4
4
2
6
图1
图2
图3
2、说出下面各图形所表示的长、宽、高各是多少?
物体所占空间的大小叫做
物体的体积
粉笔
1
、什么是物体的体积?
(一)复习
常用的体积单位有:
立方厘米
立方分米
立方米
dm
3
m
3
cm
3
棱长是1cm的正方体,体积是1cm3。
1cm
1cm
1cm
体积单位
接近1立方厘米的物体:
1dm
1dm
1dm
棱长是1dm的正方体,体积是1dm3。
接近1立方分米的物体:
棱长是1米的正方体,体积是1立方米。
1米
接近1立方米的物体:
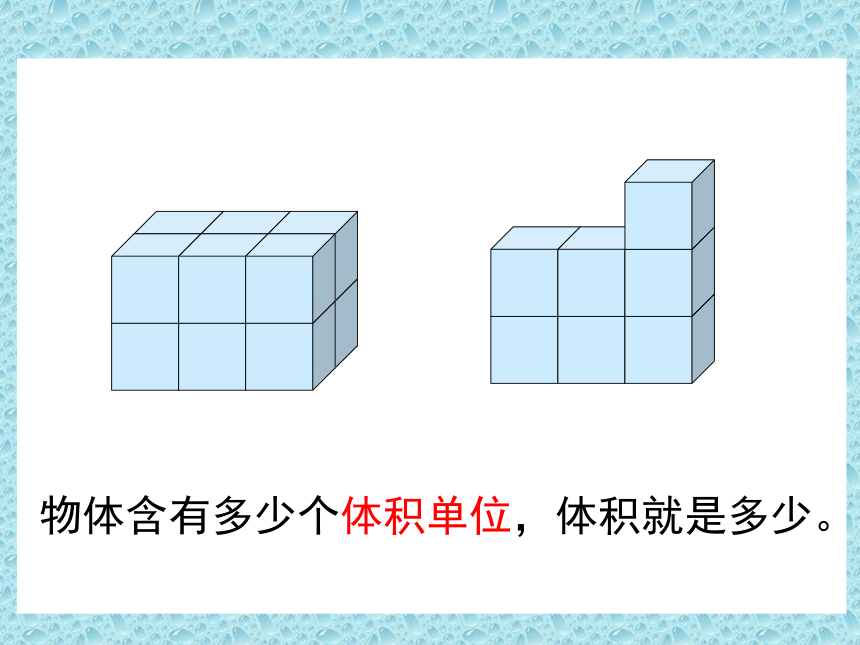
下面的图形都是由棱长为1厘米的小正方体拼成的,它们的体积各是多少呢?你是怎么知道的?
36立方厘米
24立方厘米
27立方厘米
要知道一个物体的体积,就要看这个物体含有多少个体积单位
物体含有多少个体积单位,体积就是多少。
长方体和正方体的体积
?
长方体所占空间的大小叫做长方体的体积
长方体的体积可以怎样算呢?
数体积单位个数的方法求长方体的体积
下面的长方体都是用棱长1cm的小正方体摆成的,你知道这个长方体的体积吗?
问:你是怎么知道的?
下面的长方体都是用棱长1cm的小正方体摆成的,你知道这个长方体的体积吗?
问:你是怎么知道的?
问:我们是怎样知道这些长方体体积的?
小结:我们通过数体积单位的个数知道了长方体的体积,但受客观条件的限制,有些物体是不能切割的,我们怎么知道这些物体的体积呢?今天我们就一起研究长方体和正方体体积的计算方法。
板书课题:长方体和正方体体积的计算方法
长方体的体积计算方法
观
察
操
作
用一些体积是1立方厘米的正方体拼四个不同的长方体。
观察下面的长方体,看它包含有多少个体积单位?它的体积是多少?并指出它的长、宽、高各是多少?
5
体积
5
5
长
1
1
宽
1
1
高
15
体积
5
5
长
宽
3
3
1
高
1
体积
12
3
长
3
宽
2
2
高
2
2
5
体积
5
5
长
1
1
宽
1
1
高
15
5
5
3
3
1
1
12
3
3
2
2
2
2
=
×
×
=
×
×
=
×
×
想一想:长方体的体积与它的长、宽、高
有什么关系?
长方体的体积正好是长、宽、高的乘积。
a
b
h
长
宽
高
长方体的体积=长×宽×高
V=abh
你能总结出长方体的体积计算公式吗
一个长方体,长7cm,宽4cm,高3cm,它的体积是多少?
V=abh
=7×4×3
=84(cm3)
计算下面长方体的体积
2
分米
3
分米
0.8
分米
0.
4
米
2.
2
米
6
米
V
=
abh
=
2×0.8×3
=
4.8(立方分米)
V
=
abh
=
6×2.2×0.4
=
5.28(立方米)
正方体的体积怎么样计算呢?
正方体所占空间的大小叫做正方体的体积
正方体的是特殊的长方体是长宽高都相等的长方体
长方体的体积
=
长
×
宽
×
高
棱长
棱长
棱长
棱长
棱长
棱长
正
棱长
棱长
棱长
正方体的体积
=
长
×
宽
×
高
棱长
棱长
棱长
a
a
a
V
=
a
a
a
V
=
a3
a
×
a
×
a
V
=
a3
3a
{
a
+
a
+
a
3
×
a
比较a×3和a3
a×3表示3和a相乘
a3表示3个a相乘
2、计算。
33
53
13
103
0.13
=27
=125
=1
=1000
=0.001
一块正方体石料,棱长是6dm,这块石料的体积是多少立方分米?
V
=
a3
=63
=6×6×6
=216(dm3)
答:这块石料的体积是216
dm3。
比一比:
5厘米
5厘米
5厘米
8厘米
4厘米
4厘米
v=a
=5×5×5
=125(立方厘米)
v=abh
=8×4×4
=128(立方厘米)
3
1、一块砖的长是12厘米,宽是长的一半,厚是3厘米,它的体积是多少立方厘米?
宽:12÷2=6厘米
V=abh
=
12X6X3
=216(立方厘米)
答:它的体积是216立方厘米
2、一个正方体的棱长总和是36厘米,它的
体积是多少?
棱长=36÷12
=3厘米
V=a.a.a
=3X3X3
=27立方厘米
答:它的体积是27立方厘米
2、长方体的体积=(
)
用字母表示V=(
)
长×宽×高
abh
3、正方体的体积=(
)
用字母表示V=(
)
棱长×棱长×棱长
a
×a
×a
1、物体(
)叫做物体的体积。
所占空间的大小
1.我们想要知道一个长方体的体积需要测量出这个物体的(
),(
),(
),再把它们(
),长方体体积=(
)
2.
我们想要知道一个正方体的体积只需要测量出这个物体的(
)就可以了,正方体体积=(
)
总结:
长
相乘
高
宽
棱长
长x宽x高
棱长x棱长x棱长
长方体或正方体底面的面积叫底面积。
底面
底面
长方体的体积=长×宽×高
V
=
sh
h
a
b
底面积
正方体的体积=棱长×棱长×棱长
V
=
sh
a
底面积
a
a
长方体(或正方体)的体积=底面积×高
底面
底面
V
=
sh
V
=
sh
长
横截面
长方体(或正方体)的体积=横截面×长
一根长方体木料,长5m,横截面的面积是0.06m2。这根木料的体积是多少?
0.06m2
(3)
、一个长方体的底面边长是2分米,
高是10分米,它的体积是多少立方分米?
2分米
2分米
2×2×10=40(立方分米)
建筑工地要挖一个长50m,宽30m,深50cm的长方体土坑,挖出多少方的土?
一块棱长30cm的正方体冰块,它的体积是多少立方厘米?
一块正方体石料,棱长8分米。这块石料的体积是多少立方分米?如果1立方分米的石料重3千克,这块石料重多少千克?
512×3=1536(千克)
答:这块石料的体积是512立方分米,重1536千克。
8×8×8=512(立方分米)
某体育场有一个长6.5米、宽4米、深0.5米
的长方体沙坑,已知每立方米黄沙重1.7吨,填满这个
沙坑需要用黄沙多少吨?
1.7
×(6.5
×4
×0.5)
=
1.7
×13
=
22.1(吨)
答:填满这个沙坑需要用黄沙22.1吨。
综合应用
看
谁
想
得
快?
判断题
1、一个长方体被切割成两个小长方体,
它的表面积和体积都没有改变。(
)
×
多了2个面
看
谁
想
得
快?
判断题
1、一个长方体被切割成两个小长方体,
它的表面积和体积都没有改变。(
)
×
2、一个长方体,长、宽、高都扩大2倍,
体积也扩大2倍。(
)
×
2厘米
1厘米
3厘米
2
×
1
×
3
=
2
×
3
=
6(立方厘米)
4厘米
2厘米
6厘米
4
×
2
×
6
=
8
×
6
=
48(立方厘米)
8
看谁想得快?
判断题
1、一个长方体被切割成两个小长方体,
它的表面积和体积都没有改变。(
)
?
×
2、一个长方体,长、宽、高都扩大2倍,
体积也扩大2倍。(
)
×
3、长方体的体积也可以用底面积乘以高
求得。
(
)
V=abh
长方体的体积=长×宽×高
长方体的体积=底面积×高
选择(1)如果把长方体的高扩大到3倍,长、宽都不变,那么它的体积扩大到(
)倍.
A、3
B 、6
C、9
D、27
A
(2)如果把长方体的长扩大到2倍,宽扩大到3倍,高不变,那么它的体积扩大到(
)倍.
A、2 B
、6 C、
8
D、9
B
考考你
7分米
5分米
3分米
一个长方体水箱,长7分米,宽5分米,水深3分米。把一个铁球浸
没在水中,水面升高到5分米。这个铁球的体积是多少立方分米?
5分米
★解法一:
7×5
×5-7
×5
×3
=175
-105
=70(立方分米)
答:这个铁球的体积是70立方分米。
★解法二
7×5
×(5-3)
=35
×2
=70(立方分米)
答:这个铁球的体积是70立方分米。
用12个棱长为1厘米的小正方体摆出不同的长方体
长(厘米)
宽(厘米)
高(厘米)
正方体的个数
体积(厘米3)
第一个长方体
第二个长方体
第三个长方体
第四个长方体
宽
1
cm
高
1
cm
长
12
cm
宽
2
cm
高
1
cm
长
6
cm
高
1
cm
宽
3
cm
长
4
cm
长
宽
高
长方体的体积
小木块的数量
层数高
排数宽
每排个数长
4
3
1
12
12
3
2
2
12
12
12
1
1
12
12
6
2
1
12
12
复习:
1、相交于一个顶点的三条棱的长度叫做长方体的(
)、(
)、(
)。
长
高
宽
5
5
5
4
8
3
6
2
4
5
5
5
8
3
4
4
2
6
图1
图2
图3
2、说出下面各图形所表示的长、宽、高各是多少?
物体所占空间的大小叫做
物体的体积
粉笔
1
、什么是物体的体积?
(一)复习
常用的体积单位有:
立方厘米
立方分米
立方米
dm
3
m
3
cm
3
棱长是1cm的正方体,体积是1cm3。
1cm
1cm
1cm
体积单位
接近1立方厘米的物体:
1dm
1dm
1dm
棱长是1dm的正方体,体积是1dm3。
接近1立方分米的物体:
棱长是1米的正方体,体积是1立方米。
1米
接近1立方米的物体:
下面的图形都是由棱长为1厘米的小正方体拼成的,它们的体积各是多少呢?你是怎么知道的?
36立方厘米
24立方厘米
27立方厘米
要知道一个物体的体积,就要看这个物体含有多少个体积单位
物体含有多少个体积单位,体积就是多少。
长方体和正方体的体积
?
长方体所占空间的大小叫做长方体的体积
长方体的体积可以怎样算呢?
数体积单位个数的方法求长方体的体积
下面的长方体都是用棱长1cm的小正方体摆成的,你知道这个长方体的体积吗?
问:你是怎么知道的?
下面的长方体都是用棱长1cm的小正方体摆成的,你知道这个长方体的体积吗?
问:你是怎么知道的?
问:我们是怎样知道这些长方体体积的?
小结:我们通过数体积单位的个数知道了长方体的体积,但受客观条件的限制,有些物体是不能切割的,我们怎么知道这些物体的体积呢?今天我们就一起研究长方体和正方体体积的计算方法。
板书课题:长方体和正方体体积的计算方法
长方体的体积计算方法
观
察
操
作
用一些体积是1立方厘米的正方体拼四个不同的长方体。
观察下面的长方体,看它包含有多少个体积单位?它的体积是多少?并指出它的长、宽、高各是多少?
5
体积
5
5
长
1
1
宽
1
1
高
15
体积
5
5
长
宽
3
3
1
高
1
体积
12
3
长
3
宽
2
2
高
2
2
5
体积
5
5
长
1
1
宽
1
1
高
15
5
5
3
3
1
1
12
3
3
2
2
2
2
=
×
×
=
×
×
=
×
×
想一想:长方体的体积与它的长、宽、高
有什么关系?
长方体的体积正好是长、宽、高的乘积。
a
b
h
长
宽
高
长方体的体积=长×宽×高
V=abh
你能总结出长方体的体积计算公式吗
一个长方体,长7cm,宽4cm,高3cm,它的体积是多少?
V=abh
=7×4×3
=84(cm3)
计算下面长方体的体积
2
分米
3
分米
0.8
分米
0.
4
米
2.
2
米
6
米
V
=
abh
=
2×0.8×3
=
4.8(立方分米)
V
=
abh
=
6×2.2×0.4
=
5.28(立方米)
正方体的体积怎么样计算呢?
正方体所占空间的大小叫做正方体的体积
正方体的是特殊的长方体是长宽高都相等的长方体
长方体的体积
=
长
×
宽
×
高
棱长
棱长
棱长
棱长
棱长
棱长
正
棱长
棱长
棱长
正方体的体积
=
长
×
宽
×
高
棱长
棱长
棱长
a
a
a
V
=
a
a
a
V
=
a3
a
×
a
×
a
V
=
a3
3a
{
a
+
a
+
a
3
×
a
比较a×3和a3
a×3表示3和a相乘
a3表示3个a相乘
2、计算。
33
53
13
103
0.13
=27
=125
=1
=1000
=0.001
一块正方体石料,棱长是6dm,这块石料的体积是多少立方分米?
V
=
a3
=63
=6×6×6
=216(dm3)
答:这块石料的体积是216
dm3。
比一比:
5厘米
5厘米
5厘米
8厘米
4厘米
4厘米
v=a
=5×5×5
=125(立方厘米)
v=abh
=8×4×4
=128(立方厘米)
3
1、一块砖的长是12厘米,宽是长的一半,厚是3厘米,它的体积是多少立方厘米?
宽:12÷2=6厘米
V=abh
=
12X6X3
=216(立方厘米)
答:它的体积是216立方厘米
2、一个正方体的棱长总和是36厘米,它的
体积是多少?
棱长=36÷12
=3厘米
V=a.a.a
=3X3X3
=27立方厘米
答:它的体积是27立方厘米
2、长方体的体积=(
)
用字母表示V=(
)
长×宽×高
abh
3、正方体的体积=(
)
用字母表示V=(
)
棱长×棱长×棱长
a
×a
×a
1、物体(
)叫做物体的体积。
所占空间的大小
1.我们想要知道一个长方体的体积需要测量出这个物体的(
),(
),(
),再把它们(
),长方体体积=(
)
2.
我们想要知道一个正方体的体积只需要测量出这个物体的(
)就可以了,正方体体积=(
)
总结:
长
相乘
高
宽
棱长
长x宽x高
棱长x棱长x棱长
长方体或正方体底面的面积叫底面积。
底面
底面
长方体的体积=长×宽×高
V
=
sh
h
a
b
底面积
正方体的体积=棱长×棱长×棱长
V
=
sh
a
底面积
a
a
长方体(或正方体)的体积=底面积×高
底面
底面
V
=
sh
V
=
sh
长
横截面
长方体(或正方体)的体积=横截面×长
一根长方体木料,长5m,横截面的面积是0.06m2。这根木料的体积是多少?
0.06m2
(3)
、一个长方体的底面边长是2分米,
高是10分米,它的体积是多少立方分米?
2分米
2分米
2×2×10=40(立方分米)
建筑工地要挖一个长50m,宽30m,深50cm的长方体土坑,挖出多少方的土?
一块棱长30cm的正方体冰块,它的体积是多少立方厘米?
一块正方体石料,棱长8分米。这块石料的体积是多少立方分米?如果1立方分米的石料重3千克,这块石料重多少千克?
512×3=1536(千克)
答:这块石料的体积是512立方分米,重1536千克。
8×8×8=512(立方分米)
某体育场有一个长6.5米、宽4米、深0.5米
的长方体沙坑,已知每立方米黄沙重1.7吨,填满这个
沙坑需要用黄沙多少吨?
1.7
×(6.5
×4
×0.5)
=
1.7
×13
=
22.1(吨)
答:填满这个沙坑需要用黄沙22.1吨。
综合应用
看
谁
想
得
快?
判断题
1、一个长方体被切割成两个小长方体,
它的表面积和体积都没有改变。(
)
×
多了2个面
看
谁
想
得
快?
判断题
1、一个长方体被切割成两个小长方体,
它的表面积和体积都没有改变。(
)
×
2、一个长方体,长、宽、高都扩大2倍,
体积也扩大2倍。(
)
×
2厘米
1厘米
3厘米
2
×
1
×
3
=
2
×
3
=
6(立方厘米)
4厘米
2厘米
6厘米
4
×
2
×
6
=
8
×
6
=
48(立方厘米)
8
看谁想得快?
判断题
1、一个长方体被切割成两个小长方体,
它的表面积和体积都没有改变。(
)
?
×
2、一个长方体,长、宽、高都扩大2倍,
体积也扩大2倍。(
)
×
3、长方体的体积也可以用底面积乘以高
求得。
(
)
V=abh
长方体的体积=长×宽×高
长方体的体积=底面积×高
选择(1)如果把长方体的高扩大到3倍,长、宽都不变,那么它的体积扩大到(
)倍.
A、3
B 、6
C、9
D、27
A
(2)如果把长方体的长扩大到2倍,宽扩大到3倍,高不变,那么它的体积扩大到(
)倍.
A、2 B
、6 C、
8
D、9
B
考考你
7分米
5分米
3分米
一个长方体水箱,长7分米,宽5分米,水深3分米。把一个铁球浸
没在水中,水面升高到5分米。这个铁球的体积是多少立方分米?
5分米
★解法一:
7×5
×5-7
×5
×3
=175
-105
=70(立方分米)
答:这个铁球的体积是70立方分米。
★解法二
7×5
×(5-3)
=35
×2
=70(立方分米)
答:这个铁球的体积是70立方分米。
用12个棱长为1厘米的小正方体摆出不同的长方体
长(厘米)
宽(厘米)
高(厘米)
正方体的个数
体积(厘米3)
第一个长方体
第二个长方体
第三个长方体
第四个长方体
宽
1
cm
高
1
cm
长
12
cm
宽
2
cm
高
1
cm
长
6
cm
高
1
cm
宽
3
cm
长
4
cm
长
宽
高
长方体的体积
小木块的数量
层数高
排数宽
每排个数长
4
3
1
12
12
3
2
2
12
12
12
1
1
12
12
6
2
1
12
12
