2020-2021学年高二上学期物理鲁科版(2019)必修第三册2.4带电粒子在电场中的运动课件
文档属性
| 名称 | 2020-2021学年高二上学期物理鲁科版(2019)必修第三册2.4带电粒子在电场中的运动课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-22 00:00:00 | ||
图片预览










文档简介
第2章 电势能与电势差
第4节 带电粒子在电场中的运动
课标解读
课标要求
素养形成
1.能分析带电粒子在电场中的运动情况
2.能解释相关的物理现象
1.物理观念:知道各种基本粒子的符号、质量、电荷等,知道示波管的主要构造和工作原理
2.科学思维:运用理想化方法,突出主要因素,忽略次要因素,不计粒子重力
3.科学探究:通过带电粒子运动规律的分析,培养学生的推理能力及热爱科学的精神;让学生通过讨论和思考得出知识,注重知识的建构过程
4.科学态度与责任:通过理论分析与实验验证相结合,让学生形成科学世界观,自然规律是可以理解的,我们要学习科学,利用科学知识为人类服务
精读教材·必备知识
情境导学
1.一个电子的质量为0.91×10-30 kg,电荷量e=1.6×10-19 C,g取10 m/s2,当它位于E
=5×104 V/m的电场中时,受到的重力G为多大?受到的静电力F为多大??等于
多少?你会发现什么?
提示:G=mg=9.1×10-30 N
F=qE=8×10-15 N
?≈1×1015
电子、质子、离子等微观带电粒子所受重力一般远小于静电力,重力可以忽
略(有说明或暗示除外)。
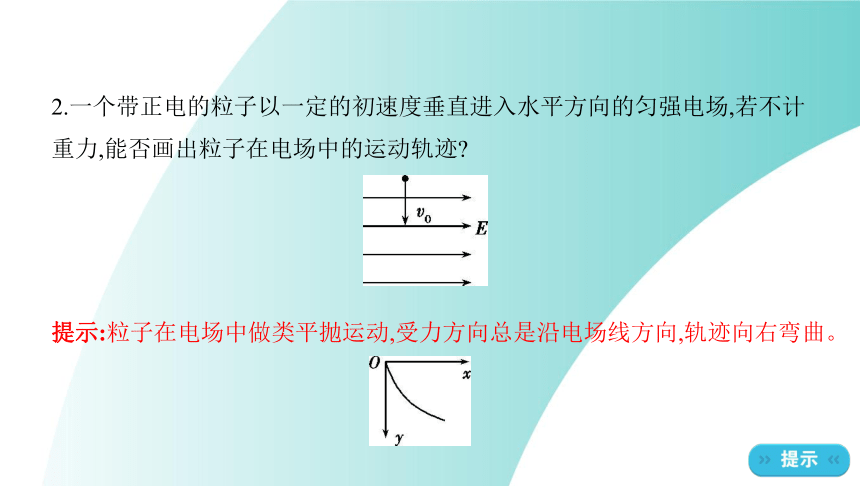
2.一个带正电的粒子以一定的初速度垂直进入水平方向的匀强电场,若不计
重力,能否画出粒子在电场中的运动轨迹?
提示:粒子在电场中做类平抛运动,受力方向总是沿电场线方向,轨迹向右弯曲。
必备知识
新知梳理
一、带电粒子加速
1.在现代科学实验和技术设备中,常常利用 ????来改变或控制带电
粒子的运动。简单情况下,利用 ????使带电粒子加速。
2.分析带电粒子加速问题的两种思路
(1)利用 ????结合匀变速直线运动公式来分析。适用于解决匀强电
场且涉及运动时间等描述运动过程的物理量的问题。
电场
电场
牛顿第二定律
(2)利用静电力做功结合 ????来分析。适用于解决只涉及位移、速
率等动能定理公式中的物理量或非匀强电场的问题。
二、带电粒子偏转
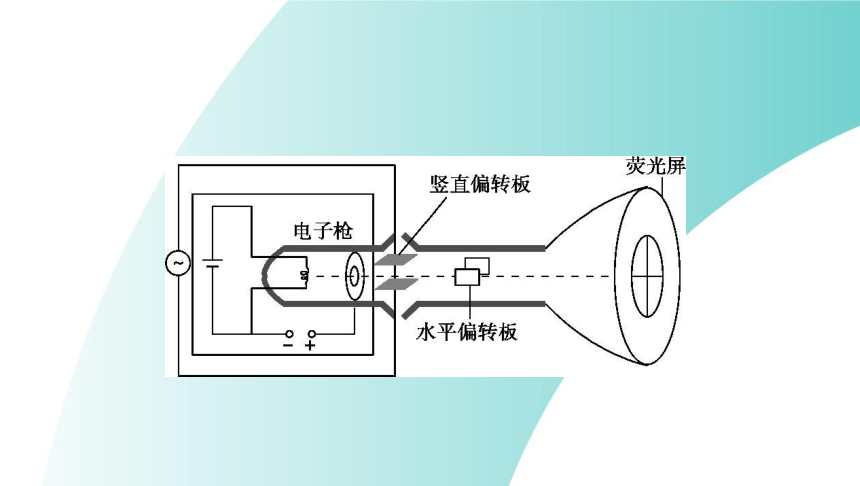
1.示波管的结构及原理
(1)构造:示波管是示波器的核心部件,由 ????、偏转电极和 ????
????组成,如图所示。
动能定理
电子枪
荧光屏
(2)工作原理
a.当竖直偏转板、水平偏转板都未加电压时,电子束从电子枪发出后沿 ????
????运动,在荧光屏上产生一个亮斑。
b.示波管实际工作时,竖直偏转板、水平偏转板都加电压,打在荧光屏上的亮
斑既在竖直方向上偏移也在水平方向上偏移,亮斑的运动就是两个方向运动
的 ????。
直线
合运动
2.带电粒子在电场中的偏转
(1)带电粒子的初速度方向跟匀强电场方向垂直时,带电粒子的运动轨迹是一
条 ????,类似平抛运动的轨迹。
(2)带电粒子沿平行于平行板电容器的方向射入匀强电场,只在静电力的作用
下做类平抛运动:
①运动性质
a.沿初速度方向: ????。
b.垂直初速度方向: ????。
抛物线
匀速直线运动
匀加速直线运动
②运动规律
a.偏移距离:因为t=?,a=?,所以偏移距离y=?at2=?。
b.偏转角度:因为vy=at=?,所以 tan θ=?=?。
思维诊断
1.基本带电粒子在电场中不受重力。?( )
2.带电粒子仅在电场力作用下运动时,动能一定增加。?( )
3.带电粒子仅在电场力作用下运动时,运动轨迹一定是直线。?( )
4.带电粒子在匀强电场中无论是直线加速还是偏转,均做匀变速运动。(???? )
5.示波管电子枪的作用是产生高速飞行的电子束,偏转电极的作用是使电子
束发生偏转,打在荧光屏的不同位置。?( )
?
?
?
√
√
要点一 带电粒子在电场中的直线运动
互动探究·关键能力
情境探究
在真空中有一对平行金属板,由于接上电池组而带电,两板间电势差为U,若一
个质量为m、带正电荷量为q的粒子,以初速度v0从正极板附近向负极板运动。
试结合上述情境讨论:
1.怎样计算它到达负极板时的速度?
提示:由动能定理有qU=?mv2-?m?,得v=?。
2.若粒子带的是负电荷(初速度为v0),将做匀减速直线运动,如果能到达负极
板,则到达负极板时速度大小是多少?
提示:由动能定理有-qU=?mv2-?m?,得v=?。
3.上述问题中,两块金属板是平行的,两板间的电场是匀强电场,如果两金属板
是其他形状,中间的电场不再均匀,上面的结果是否仍然适用?为什么?
提示:结果仍然适用。因为不管是否为匀强电场,静电力做功都可以用W=qU
计算,动能定理仍然适用。
知识深化
1.粒子做直线运动的条件
(1)粒子所受合外力F合=0,粒子静止或做匀速直线运动。
(2)粒子所受合外力F合≠0,且与初速度方向在同一条直线上,带电粒子将做匀
加速直线运动或匀减速直线运动。
项目
动力学角度
功能关系角度
应用知识
牛顿第二定律以及匀变速直线运动公式
功的公式及动能定理
适用条件
匀强电场,静电力是恒力
匀强电场、非匀强电场;静电力是恒力、变力
2.处理带电粒子在电场中加速问题的两个角度
题组过关
典例1 如图所示,一个质子以初速度v0=5×106 m/s水平射入一个由两块带电
的平行金属板组成的区域。两板距离为20 cm,设金属板之间电场是匀强电
场,电场强度为3×105 N/C。质子质量m=1.67×10-27 kg,电荷量q=1.60×10-19 C。
求:
(1)质子由板上小孔射出时的速度大小;
(2)若质子刚好不能从小孔中射出,其他条件不变,则金属板之间的电场强度
至少为多大?方向如何?
?
解析 (1)根据动能定理
W=?m?-?m?
而W=qEd=1.60×10-19×3×105×0.2 J=9.6×10-15 J
所以v1=?=? m/s≈6×106 m/s
质子飞出时的速度约为6×106 m/s。
(2)若质子刚好不能从小孔中射出,根据动能定理-qE'd=0-?m?,则E'=?=
? N/C≈6.5×105 N/C,方向水平向左。
答案 (1)6×106 m/s (2)6.5×105 N/C 方向水平向左
特别提醒
带电粒子在电场中的重力问题
(1)基本粒子:如电子、质子、α粒子、离子等除有说明或有明确的暗示以外,
一般都不考虑重力(但并不忽略质量)。
(2)带电颗粒:如液滴、油滴、尘埃、小球等,除有说明或有明确的暗示以外,
一般都不能忽略重力。
针对训练1????(多选)示波管中电子枪的原理示意图如图所示,示波管内被抽成
真空。A为发射电子的阴极,K为接在高电势点的加速阳极,A、K间电压为U,
电子离开阴极时的速度可以忽略,电子经加速后从K的小孔
中射出时的速度大小为v。下面的说法正确的是?( )
A.如果A、K间距离减半而电压仍为U,则电子离开K时的速度仍为v
B.如果A、K间距离减半而电压仍为U,则电子离开K时的速度变为?
C.如果A、K间距离不变而电压减半,则电子离开K时的速度变为?v
D.如果A、K间距离不变而电压减半,则电子离开K时的速度变为?
AC
解析 电子在两个电极间的加速电场中进行加速,由动能定理eU=?mv2-0
得v=?,当电压不变,A、K间距离变化时,不影响电子的速度,故A正确,B
错误;电压减半,则电子离开K时的速度为?v,C正确,D错误。
针对训练2 如图所示,两块水平放置的平行金属板与电源连接,上、下板分
别带正、负电荷。油滴从喷雾器喷出后,由于摩擦而带负电,油滴进入上板中
央小孔后落到匀强电场中,通过显微镜可以观察到油滴的运动情况。两金属
板间的距离为d,忽略空气对油滴的浮力和阻力。
若油滴进入电场时的速度可以忽略,当两金属板
间的电势差为U时,观察到某个质量为m的油滴
进入电场后做匀加速运动,经过时间t运动到下
极板。重力加速度为g,求该油滴所带电荷量。
答案??????
解析 油滴进入电场后做匀加速运动,
由牛顿第二定律得mg-q?=ma?①
根据位移时间公式得d=?at2?②
①②联立解得q=??。
要点二 带电粒子在电场中的偏转
如图所示,质量为m、电荷量为q的粒子以初速度v0垂直于电场方向射入两极
板间,两平行板间存在方向竖直向下的匀强电场,已知板长为l,板间电压为U,
板间距为d,不计粒子的重力,假设粒子能飞出极板。
情境探究
请根据上述情境回答下列问题:
1.带电粒子在垂直于电场方向做什么运动?
提示:匀速直线运动。
2.带电粒子在沿电场方向做什么运动?
提示:初速度为零的匀加速直线运动。
3.怎样求带电粒子在电场中运动的时间?
提示:t=?。
4.粒子所受静电力多大?加速度多大?
提示:F=q?,a=?=?。
5.带电粒子在沿电场方向的偏转距离为多少?
提示:y=??·?=?。
6.粒子离开电场时沿电场方向的速度大小是多少?
提示:vy=?·?=?。
7.求粒子离开电场时的速度大小和方向。
提示:v=?=?,tan θ=?=?。
知识深化
1.带电粒子在匀强电场中偏转的基本规律
初速度方向:vx=v0,l=v0t。
电场线方向:vy=at,y=?at2。
2.偏转位移和偏转角
(1)粒子离开电场时的偏转位移y=?at2=???=?。
(2)粒子离开电场时的偏转角 tan θ=?=?。
(3)粒子离开电场时位移与初速度夹角的正切值 tan α=?=?。
3.两个常用的推论
(1)粒子射出电场时好像从板长l的?处沿直线射出。
(2)位移方向与初速度方向夹角的正切值为速度偏转角正切值的?,即 tan α=?
tan θ。
4.运动轨迹:抛物线。
题组过关
典例2 一束电子流在经U=5 000 V的加速电压加速后,在距两极板相等位置
处垂直进入平行板间的匀强电场,如图所示。若两板间距d=1.0 cm,板长l=5.0
cm,那么要使电子能从平行板间飞出,两个极板上最大能加多大电压?若使电
子打到下板中间,其他条件不变,则两个极板上需要加多大的电压?
答案 400 V 1 600 V
解析 加速过程,由动能定理得
eU=?m??①
进入偏转电场,电子在平行于板面的方向上做匀速直线运动l=v0t?②
在垂直于板面的方向上做匀加速直线运动
加速度a=?=??③
偏转距离y=?at2?④
能飞出的条件为y≤??⑤
联立①~⑤式解得U'≤?=400 V
即要使电子能飞出,所加电压最大为400 V。
若使电子打到下板中间,由eU=?m?
a=?
?=?at2
?=v0t
联立解得U″=?=1 600 V。
规律方法
带电粒子在电场中运动问题的两种求解思路
1.运动学与动力学观点
①带电粒子初速度方向与电场线共线,则粒子做匀变速直线运动;
②带电粒子的初速度方向垂直电场线,则粒子做匀变速曲线运动(类平抛运
动)。
③当带电粒子在电场中做匀变速曲线运动时,一般要采取类似平抛运动的解
决方法。
2.功能观点
①若选用动能定理,则要分清有多少个力做功,是恒力做功还是变力做功,同
时要明确初、末状态及运动过程中的动能的变化量。
②若选用能量守恒定律,则要分清带电粒子在运动中共有多少种能量参与转
化,哪些能量是增加的,哪些能量是减少的。
针对训练3 如图所示,从炽热的金属丝逸出的电子(速度可视为零),经加速
电场加速后从两极板中间垂直射入偏转电场。电子的重力不计。在满足电
子能射出偏转电场的条件下,下述四种情况中,一定能使电子的偏转角变大的
是?( )
A.仅将偏转电场极性对调
B.仅增大偏转电极间的距离
C.仅增大偏转电极间的电压
D.仅减小偏转电极间的电压
C
解析 设加速电场的电压为U0,偏转电压为U,极板长度为L,间距为d,电子加
速过程中,由U0e=?,得v0=?,电子进入极板间后做类平抛运动,时间t=
?,加速度a=?,竖直分速度vy=at,tan θ=?=?,故可知C正确。
针对训练4????(多选)如图所示,M、N是竖直放置的两平行金属板,分别带等量
异种电荷,两板间产生一个水平向右的匀强电场,电场强度为E,一质量为m、
电荷量为+q的微粒以初速度v0沿竖直向上方向从与两板等距的A点射入匀强
电场中,在静电力的作用下垂直打到N板上的C点,已知AB=BC。不计空气阻
力,g为重力加速度,则可知?( )
AB
A.微粒在电场中做曲线运动
B.微粒打到C点时的速率与射入电场时的速率相等
C.M、N板间的电势差为?
D.M、N板间的电势差为?
解析 由题意可知,微粒受水平向右的静电力qE和竖直向下的重力mg作
用,合力与v0不共线,所以微粒做曲线运动,A正确;因AB=BC,即?·t=?·t,故vC=
v0,B正确;由q·?=?m?,得U=?=?,C错误;由mg=qE,得q=?,代入U=?,
得U=?,D错误。
评价检测·素养提升
课堂检测
1.一带电粒子在电场中只受静电力作用时,它不可能出现的运动状态是?
(???? )
A.匀速直线运动 ???? B.匀加速直线运动
C.匀变速曲线运动 ???? D.匀速圆周运动
解析 因为粒子只受到静电力的作用,所以不可能做匀速直线运动。
A
2.喷墨打印机的简化模型如图所示。重力可忽略的墨汁微滴,经带电室带负
电后,以速度v沿垂直于匀强电场方向飞入极板间,最终打在纸上,则微滴在极
板间电场中?( )
A.向负极板偏转
B.电势能逐渐增大
C.运动轨迹是抛物线
D.运动轨迹与带电荷量无关
C
解析 由于微滴带负电,其所受静电力指向正极板,故微滴在极板间电场中
向正极板偏转,A项错误。微滴在极板间电场中所受静电力做正功,电势能减
小,B项错误。由于极板间电场是匀强电场,静电力不变,故微滴在极板间电场
中做匀变速曲线运动,并且轨迹为抛物线,C项正确。微滴所带电荷量影响静
电力及其加速度大小,运动轨迹与加速度大小有关,故D项错误。
3.电子以初速度v0沿垂直电场方向射入两平行金属板中间的匀强电场中,现
增大两板间的电压,但仍能使电子穿过该电场。则电子穿越平行板间的电场
所需时间?( )
A.随电压的增大而减小 ???? B.随电压的增大而增大
C.与电压无关 ???? D.不能判定是否与电压有关
解析 电子以初速度v0沿垂直电场方向射入两平行金属板间的匀强电场后,
做类平抛运动,垂直电场方向做匀速直线运动,设板长为l,由于电子始终能穿
过电场,则电子穿越电场的时间t=?,与两极板间电压无关,C正确。
C
4.如图所示,在P板附近有一电子由静止开始向Q板
运动。已知两极板间电势差为U,板间距为d,电子
质量为m,电荷量为e。则关于电子在两板间的运
动情况,下列说法正确的是?( )
A.若将板间距d增大一倍,则电子到达Q板时的速率保持不变
B.若将板间距d增大一倍,则电子到达Q板时的速率也增大一倍
C.若将两极板间电势差U增大一倍,则电子到达Q板的时间保持不变
D.若将两极板间电势差U增大一倍,则电子到达Q板的时间减为一半
A
解析 根据动能定理得,eU=?mv2知,电子到达Q板的速度v=?,将板间距
增大一倍,电子到达Q板的速率不变,故A正确,B错误。电子的加速度大小a=
?=?,根据d=?at2得,t=?,U增大一倍,则电子到达Q板的时间变为原来
的?,故C、D错误。
等效思维方法就是将一个复杂的物理问题,等效为一个熟知的物理模型或问
题的方法。例如我们学习过的分力与合力、合运动与分运动等都体现了等
效思维方法。常见的等效法有“分解”“合成”“等效类比”“等效替
换”“等效变换”“等效简化”等,从而化繁为简,化难为易。
带电体在匀强电场和重力场组成的复合场中做圆周运动的问题,是高中物理
教学中一类重要而典型的题型。对于这类问题,若采用常规方法求解,过程复
杂,运算量大。若采用“等效法”求解,则能避开复杂的运算,过程比较简
创新视野
捷。先求出重力与静电力的合力,将这个合力视为一个“等效重力”,将a=
?视为“等效重力加速度”。再将物体在重力场中做圆周运动的规律迁移
到等效重力场中分析求解即可。
1.一个带负电荷量为q,质量为m的小球,从光滑绝缘的斜面轨道的A点由静止
下滑,小球恰能通过半径为R的竖直圆形轨道的最高点B而做圆周运动。现在
竖直方向上加如图所示的匀强电场,若仍从A点由静止释放该小球,则?(???? )
A.小球不能过B点
B.小球仍恰好能过B点
C.小球能过B点,且在B点与轨道之间压力不为0
D.以上说法都不对
B
解析 没有电场时,设小球在最高点B速度为v,则mg=m?
又根据机械能守恒定律,有:mg(h-2R)=?mv2
解得:h=?R
加上电场时,恰好过最高点需要的速度设为v',则:mg-qE=m?
解得:v'=?
根据动能定理,得mg(h-2R)-qE(h-2R)=?mv″2,
解得:v″=?
说明小球仍恰好能过B点,且与轨道间无作用力,故B正确。
2.在竖直平面内有水平向右、电场强度大小为E的匀强电场,在匀强电场中有一根长为L的绝缘细线,一端固定在O点,另一端系一质量为m的带电小球,
它静止时位于A点,此时细线与竖直方向成37°角,如图所示。现给小球一沿与细线方向垂直的速度,使小球能绕O点在竖直平面内做完整的圆周运动。下列对小球运动的分析正确的是(不考虑空气阻力,细线不会缠绕在O点上)?( )
D
A.小球运动到C点时动能最小
B.小球运动到C点时细线拉力最小
C.小球运动到Q点时动能最大
D.小球运动到B点时机械能最大
解析 由题意可知,小球所受的静电力与重力的合力沿OA方向,小球从A点
开始无论向哪运动,合力对小球都做负功,小球动能将减小,所以运动到A点时
动能最大,C错误;小球运动到与A点关于圆心对称的点时动能最小,在该点时
细线的拉力最小,A、B错误;小球在运动过程中,运动到B点时静电力做功最
多,因此机械能最大,D正确。
第4节 带电粒子在电场中的运动
课标解读
课标要求
素养形成
1.能分析带电粒子在电场中的运动情况
2.能解释相关的物理现象
1.物理观念:知道各种基本粒子的符号、质量、电荷等,知道示波管的主要构造和工作原理
2.科学思维:运用理想化方法,突出主要因素,忽略次要因素,不计粒子重力
3.科学探究:通过带电粒子运动规律的分析,培养学生的推理能力及热爱科学的精神;让学生通过讨论和思考得出知识,注重知识的建构过程
4.科学态度与责任:通过理论分析与实验验证相结合,让学生形成科学世界观,自然规律是可以理解的,我们要学习科学,利用科学知识为人类服务
精读教材·必备知识
情境导学
1.一个电子的质量为0.91×10-30 kg,电荷量e=1.6×10-19 C,g取10 m/s2,当它位于E
=5×104 V/m的电场中时,受到的重力G为多大?受到的静电力F为多大??等于
多少?你会发现什么?
提示:G=mg=9.1×10-30 N
F=qE=8×10-15 N
?≈1×1015
电子、质子、离子等微观带电粒子所受重力一般远小于静电力,重力可以忽
略(有说明或暗示除外)。
2.一个带正电的粒子以一定的初速度垂直进入水平方向的匀强电场,若不计
重力,能否画出粒子在电场中的运动轨迹?
提示:粒子在电场中做类平抛运动,受力方向总是沿电场线方向,轨迹向右弯曲。
必备知识
新知梳理
一、带电粒子加速
1.在现代科学实验和技术设备中,常常利用 ????来改变或控制带电
粒子的运动。简单情况下,利用 ????使带电粒子加速。
2.分析带电粒子加速问题的两种思路
(1)利用 ????结合匀变速直线运动公式来分析。适用于解决匀强电
场且涉及运动时间等描述运动过程的物理量的问题。
电场
电场
牛顿第二定律
(2)利用静电力做功结合 ????来分析。适用于解决只涉及位移、速
率等动能定理公式中的物理量或非匀强电场的问题。
二、带电粒子偏转
1.示波管的结构及原理
(1)构造:示波管是示波器的核心部件,由 ????、偏转电极和 ????
????组成,如图所示。
动能定理
电子枪
荧光屏
(2)工作原理
a.当竖直偏转板、水平偏转板都未加电压时,电子束从电子枪发出后沿 ????
????运动,在荧光屏上产生一个亮斑。
b.示波管实际工作时,竖直偏转板、水平偏转板都加电压,打在荧光屏上的亮
斑既在竖直方向上偏移也在水平方向上偏移,亮斑的运动就是两个方向运动
的 ????。
直线
合运动
2.带电粒子在电场中的偏转
(1)带电粒子的初速度方向跟匀强电场方向垂直时,带电粒子的运动轨迹是一
条 ????,类似平抛运动的轨迹。
(2)带电粒子沿平行于平行板电容器的方向射入匀强电场,只在静电力的作用
下做类平抛运动:
①运动性质
a.沿初速度方向: ????。
b.垂直初速度方向: ????。
抛物线
匀速直线运动
匀加速直线运动
②运动规律
a.偏移距离:因为t=?,a=?,所以偏移距离y=?at2=?。
b.偏转角度:因为vy=at=?,所以 tan θ=?=?。
思维诊断
1.基本带电粒子在电场中不受重力。?( )
2.带电粒子仅在电场力作用下运动时,动能一定增加。?( )
3.带电粒子仅在电场力作用下运动时,运动轨迹一定是直线。?( )
4.带电粒子在匀强电场中无论是直线加速还是偏转,均做匀变速运动。(???? )
5.示波管电子枪的作用是产生高速飞行的电子束,偏转电极的作用是使电子
束发生偏转,打在荧光屏的不同位置。?( )
?
?
?
√
√
要点一 带电粒子在电场中的直线运动
互动探究·关键能力
情境探究
在真空中有一对平行金属板,由于接上电池组而带电,两板间电势差为U,若一
个质量为m、带正电荷量为q的粒子,以初速度v0从正极板附近向负极板运动。
试结合上述情境讨论:
1.怎样计算它到达负极板时的速度?
提示:由动能定理有qU=?mv2-?m?,得v=?。
2.若粒子带的是负电荷(初速度为v0),将做匀减速直线运动,如果能到达负极
板,则到达负极板时速度大小是多少?
提示:由动能定理有-qU=?mv2-?m?,得v=?。
3.上述问题中,两块金属板是平行的,两板间的电场是匀强电场,如果两金属板
是其他形状,中间的电场不再均匀,上面的结果是否仍然适用?为什么?
提示:结果仍然适用。因为不管是否为匀强电场,静电力做功都可以用W=qU
计算,动能定理仍然适用。
知识深化
1.粒子做直线运动的条件
(1)粒子所受合外力F合=0,粒子静止或做匀速直线运动。
(2)粒子所受合外力F合≠0,且与初速度方向在同一条直线上,带电粒子将做匀
加速直线运动或匀减速直线运动。
项目
动力学角度
功能关系角度
应用知识
牛顿第二定律以及匀变速直线运动公式
功的公式及动能定理
适用条件
匀强电场,静电力是恒力
匀强电场、非匀强电场;静电力是恒力、变力
2.处理带电粒子在电场中加速问题的两个角度
题组过关
典例1 如图所示,一个质子以初速度v0=5×106 m/s水平射入一个由两块带电
的平行金属板组成的区域。两板距离为20 cm,设金属板之间电场是匀强电
场,电场强度为3×105 N/C。质子质量m=1.67×10-27 kg,电荷量q=1.60×10-19 C。
求:
(1)质子由板上小孔射出时的速度大小;
(2)若质子刚好不能从小孔中射出,其他条件不变,则金属板之间的电场强度
至少为多大?方向如何?
?
解析 (1)根据动能定理
W=?m?-?m?
而W=qEd=1.60×10-19×3×105×0.2 J=9.6×10-15 J
所以v1=?=? m/s≈6×106 m/s
质子飞出时的速度约为6×106 m/s。
(2)若质子刚好不能从小孔中射出,根据动能定理-qE'd=0-?m?,则E'=?=
? N/C≈6.5×105 N/C,方向水平向左。
答案 (1)6×106 m/s (2)6.5×105 N/C 方向水平向左
特别提醒
带电粒子在电场中的重力问题
(1)基本粒子:如电子、质子、α粒子、离子等除有说明或有明确的暗示以外,
一般都不考虑重力(但并不忽略质量)。
(2)带电颗粒:如液滴、油滴、尘埃、小球等,除有说明或有明确的暗示以外,
一般都不能忽略重力。
针对训练1????(多选)示波管中电子枪的原理示意图如图所示,示波管内被抽成
真空。A为发射电子的阴极,K为接在高电势点的加速阳极,A、K间电压为U,
电子离开阴极时的速度可以忽略,电子经加速后从K的小孔
中射出时的速度大小为v。下面的说法正确的是?( )
A.如果A、K间距离减半而电压仍为U,则电子离开K时的速度仍为v
B.如果A、K间距离减半而电压仍为U,则电子离开K时的速度变为?
C.如果A、K间距离不变而电压减半,则电子离开K时的速度变为?v
D.如果A、K间距离不变而电压减半,则电子离开K时的速度变为?
AC
解析 电子在两个电极间的加速电场中进行加速,由动能定理eU=?mv2-0
得v=?,当电压不变,A、K间距离变化时,不影响电子的速度,故A正确,B
错误;电压减半,则电子离开K时的速度为?v,C正确,D错误。
针对训练2 如图所示,两块水平放置的平行金属板与电源连接,上、下板分
别带正、负电荷。油滴从喷雾器喷出后,由于摩擦而带负电,油滴进入上板中
央小孔后落到匀强电场中,通过显微镜可以观察到油滴的运动情况。两金属
板间的距离为d,忽略空气对油滴的浮力和阻力。
若油滴进入电场时的速度可以忽略,当两金属板
间的电势差为U时,观察到某个质量为m的油滴
进入电场后做匀加速运动,经过时间t运动到下
极板。重力加速度为g,求该油滴所带电荷量。
答案??????
解析 油滴进入电场后做匀加速运动,
由牛顿第二定律得mg-q?=ma?①
根据位移时间公式得d=?at2?②
①②联立解得q=??。
要点二 带电粒子在电场中的偏转
如图所示,质量为m、电荷量为q的粒子以初速度v0垂直于电场方向射入两极
板间,两平行板间存在方向竖直向下的匀强电场,已知板长为l,板间电压为U,
板间距为d,不计粒子的重力,假设粒子能飞出极板。
情境探究
请根据上述情境回答下列问题:
1.带电粒子在垂直于电场方向做什么运动?
提示:匀速直线运动。
2.带电粒子在沿电场方向做什么运动?
提示:初速度为零的匀加速直线运动。
3.怎样求带电粒子在电场中运动的时间?
提示:t=?。
4.粒子所受静电力多大?加速度多大?
提示:F=q?,a=?=?。
5.带电粒子在沿电场方向的偏转距离为多少?
提示:y=??·?=?。
6.粒子离开电场时沿电场方向的速度大小是多少?
提示:vy=?·?=?。
7.求粒子离开电场时的速度大小和方向。
提示:v=?=?,tan θ=?=?。
知识深化
1.带电粒子在匀强电场中偏转的基本规律
初速度方向:vx=v0,l=v0t。
电场线方向:vy=at,y=?at2。
2.偏转位移和偏转角
(1)粒子离开电场时的偏转位移y=?at2=???=?。
(2)粒子离开电场时的偏转角 tan θ=?=?。
(3)粒子离开电场时位移与初速度夹角的正切值 tan α=?=?。
3.两个常用的推论
(1)粒子射出电场时好像从板长l的?处沿直线射出。
(2)位移方向与初速度方向夹角的正切值为速度偏转角正切值的?,即 tan α=?
tan θ。
4.运动轨迹:抛物线。
题组过关
典例2 一束电子流在经U=5 000 V的加速电压加速后,在距两极板相等位置
处垂直进入平行板间的匀强电场,如图所示。若两板间距d=1.0 cm,板长l=5.0
cm,那么要使电子能从平行板间飞出,两个极板上最大能加多大电压?若使电
子打到下板中间,其他条件不变,则两个极板上需要加多大的电压?
答案 400 V 1 600 V
解析 加速过程,由动能定理得
eU=?m??①
进入偏转电场,电子在平行于板面的方向上做匀速直线运动l=v0t?②
在垂直于板面的方向上做匀加速直线运动
加速度a=?=??③
偏转距离y=?at2?④
能飞出的条件为y≤??⑤
联立①~⑤式解得U'≤?=400 V
即要使电子能飞出,所加电压最大为400 V。
若使电子打到下板中间,由eU=?m?
a=?
?=?at2
?=v0t
联立解得U″=?=1 600 V。
规律方法
带电粒子在电场中运动问题的两种求解思路
1.运动学与动力学观点
①带电粒子初速度方向与电场线共线,则粒子做匀变速直线运动;
②带电粒子的初速度方向垂直电场线,则粒子做匀变速曲线运动(类平抛运
动)。
③当带电粒子在电场中做匀变速曲线运动时,一般要采取类似平抛运动的解
决方法。
2.功能观点
①若选用动能定理,则要分清有多少个力做功,是恒力做功还是变力做功,同
时要明确初、末状态及运动过程中的动能的变化量。
②若选用能量守恒定律,则要分清带电粒子在运动中共有多少种能量参与转
化,哪些能量是增加的,哪些能量是减少的。
针对训练3 如图所示,从炽热的金属丝逸出的电子(速度可视为零),经加速
电场加速后从两极板中间垂直射入偏转电场。电子的重力不计。在满足电
子能射出偏转电场的条件下,下述四种情况中,一定能使电子的偏转角变大的
是?( )
A.仅将偏转电场极性对调
B.仅增大偏转电极间的距离
C.仅增大偏转电极间的电压
D.仅减小偏转电极间的电压
C
解析 设加速电场的电压为U0,偏转电压为U,极板长度为L,间距为d,电子加
速过程中,由U0e=?,得v0=?,电子进入极板间后做类平抛运动,时间t=
?,加速度a=?,竖直分速度vy=at,tan θ=?=?,故可知C正确。
针对训练4????(多选)如图所示,M、N是竖直放置的两平行金属板,分别带等量
异种电荷,两板间产生一个水平向右的匀强电场,电场强度为E,一质量为m、
电荷量为+q的微粒以初速度v0沿竖直向上方向从与两板等距的A点射入匀强
电场中,在静电力的作用下垂直打到N板上的C点,已知AB=BC。不计空气阻
力,g为重力加速度,则可知?( )
AB
A.微粒在电场中做曲线运动
B.微粒打到C点时的速率与射入电场时的速率相等
C.M、N板间的电势差为?
D.M、N板间的电势差为?
解析 由题意可知,微粒受水平向右的静电力qE和竖直向下的重力mg作
用,合力与v0不共线,所以微粒做曲线运动,A正确;因AB=BC,即?·t=?·t,故vC=
v0,B正确;由q·?=?m?,得U=?=?,C错误;由mg=qE,得q=?,代入U=?,
得U=?,D错误。
评价检测·素养提升
课堂检测
1.一带电粒子在电场中只受静电力作用时,它不可能出现的运动状态是?
(???? )
A.匀速直线运动 ???? B.匀加速直线运动
C.匀变速曲线运动 ???? D.匀速圆周运动
解析 因为粒子只受到静电力的作用,所以不可能做匀速直线运动。
A
2.喷墨打印机的简化模型如图所示。重力可忽略的墨汁微滴,经带电室带负
电后,以速度v沿垂直于匀强电场方向飞入极板间,最终打在纸上,则微滴在极
板间电场中?( )
A.向负极板偏转
B.电势能逐渐增大
C.运动轨迹是抛物线
D.运动轨迹与带电荷量无关
C
解析 由于微滴带负电,其所受静电力指向正极板,故微滴在极板间电场中
向正极板偏转,A项错误。微滴在极板间电场中所受静电力做正功,电势能减
小,B项错误。由于极板间电场是匀强电场,静电力不变,故微滴在极板间电场
中做匀变速曲线运动,并且轨迹为抛物线,C项正确。微滴所带电荷量影响静
电力及其加速度大小,运动轨迹与加速度大小有关,故D项错误。
3.电子以初速度v0沿垂直电场方向射入两平行金属板中间的匀强电场中,现
增大两板间的电压,但仍能使电子穿过该电场。则电子穿越平行板间的电场
所需时间?( )
A.随电压的增大而减小 ???? B.随电压的增大而增大
C.与电压无关 ???? D.不能判定是否与电压有关
解析 电子以初速度v0沿垂直电场方向射入两平行金属板间的匀强电场后,
做类平抛运动,垂直电场方向做匀速直线运动,设板长为l,由于电子始终能穿
过电场,则电子穿越电场的时间t=?,与两极板间电压无关,C正确。
C
4.如图所示,在P板附近有一电子由静止开始向Q板
运动。已知两极板间电势差为U,板间距为d,电子
质量为m,电荷量为e。则关于电子在两板间的运
动情况,下列说法正确的是?( )
A.若将板间距d增大一倍,则电子到达Q板时的速率保持不变
B.若将板间距d增大一倍,则电子到达Q板时的速率也增大一倍
C.若将两极板间电势差U增大一倍,则电子到达Q板的时间保持不变
D.若将两极板间电势差U增大一倍,则电子到达Q板的时间减为一半
A
解析 根据动能定理得,eU=?mv2知,电子到达Q板的速度v=?,将板间距
增大一倍,电子到达Q板的速率不变,故A正确,B错误。电子的加速度大小a=
?=?,根据d=?at2得,t=?,U增大一倍,则电子到达Q板的时间变为原来
的?,故C、D错误。
等效思维方法就是将一个复杂的物理问题,等效为一个熟知的物理模型或问
题的方法。例如我们学习过的分力与合力、合运动与分运动等都体现了等
效思维方法。常见的等效法有“分解”“合成”“等效类比”“等效替
换”“等效变换”“等效简化”等,从而化繁为简,化难为易。
带电体在匀强电场和重力场组成的复合场中做圆周运动的问题,是高中物理
教学中一类重要而典型的题型。对于这类问题,若采用常规方法求解,过程复
杂,运算量大。若采用“等效法”求解,则能避开复杂的运算,过程比较简
创新视野
捷。先求出重力与静电力的合力,将这个合力视为一个“等效重力”,将a=
?视为“等效重力加速度”。再将物体在重力场中做圆周运动的规律迁移
到等效重力场中分析求解即可。
1.一个带负电荷量为q,质量为m的小球,从光滑绝缘的斜面轨道的A点由静止
下滑,小球恰能通过半径为R的竖直圆形轨道的最高点B而做圆周运动。现在
竖直方向上加如图所示的匀强电场,若仍从A点由静止释放该小球,则?(???? )
A.小球不能过B点
B.小球仍恰好能过B点
C.小球能过B点,且在B点与轨道之间压力不为0
D.以上说法都不对
B
解析 没有电场时,设小球在最高点B速度为v,则mg=m?
又根据机械能守恒定律,有:mg(h-2R)=?mv2
解得:h=?R
加上电场时,恰好过最高点需要的速度设为v',则:mg-qE=m?
解得:v'=?
根据动能定理,得mg(h-2R)-qE(h-2R)=?mv″2,
解得:v″=?
说明小球仍恰好能过B点,且与轨道间无作用力,故B正确。
2.在竖直平面内有水平向右、电场强度大小为E的匀强电场,在匀强电场中有一根长为L的绝缘细线,一端固定在O点,另一端系一质量为m的带电小球,
它静止时位于A点,此时细线与竖直方向成37°角,如图所示。现给小球一沿与细线方向垂直的速度,使小球能绕O点在竖直平面内做完整的圆周运动。下列对小球运动的分析正确的是(不考虑空气阻力,细线不会缠绕在O点上)?( )
D
A.小球运动到C点时动能最小
B.小球运动到C点时细线拉力最小
C.小球运动到Q点时动能最大
D.小球运动到B点时机械能最大
解析 由题意可知,小球所受的静电力与重力的合力沿OA方向,小球从A点
开始无论向哪运动,合力对小球都做负功,小球动能将减小,所以运动到A点时
动能最大,C错误;小球运动到与A点关于圆心对称的点时动能最小,在该点时
细线的拉力最小,A、B错误;小球在运动过程中,运动到B点时静电力做功最
多,因此机械能最大,D正确。
同课章节目录
- 第1章 静电力与电场强度
- 第1节 静电的产生及其微观解释
- 第2节 库仑定律
- 第3节 电场与电场强度
- 第4节 点电荷的电场 匀强电场
- 第5节 静电的利用与防护
- 第2章 电势能与电势差
- 第1节 静电力做功与电势能
- 第2节 电势与等势面
- 第3节 电势差与电场强度的关系
- 第4节 带电粒子在电场中的运动
- 第5节 科学探究:电容器
- 第3章 恒定电流
- 第1节 电流
- 第2节 电阻
- 第3节 电功与电热
- 第4节 串联电路和并联电路
- 第5节 科学测量:长度的测量及测量工具的选用
- 第6节 科学测量:金属丝的电阻率
- 第4章 闭合电路欧姆定律与科学用电
- 第1节 闭合电路欧姆定律
- 第2节 科学测量:电源的电动势和内阻
- 第3节 科学测量:用多用电表测量电学量
- 第4节 科学用电
- 第5章 初识电磁场与电磁波
- 第1节 磁场及其描述
- 第2节 电磁感应现象及其应用
- 第3节 初识电磁波及其应用
- 第4节 初识光量子与量子世界
- 第6章 能源与可持续发展
- 第1节 能量的多种形式
- 第2节 能量的转化与守恒
- 第3节 珍惜大自然
