2020-2021学年高二上学期物理鲁科版(2019)必修第三册第2章电势能与电势差 章末总结课件32张PPT
文档属性
| 名称 | 2020-2021学年高二上学期物理鲁科版(2019)必修第三册第2章电势能与电势差 章末总结课件32张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-22 20:25:56 | ||
图片预览










文档简介
第2章 电势能与电势差
章末总结
要点一 电场中的功能关系
整合归纳
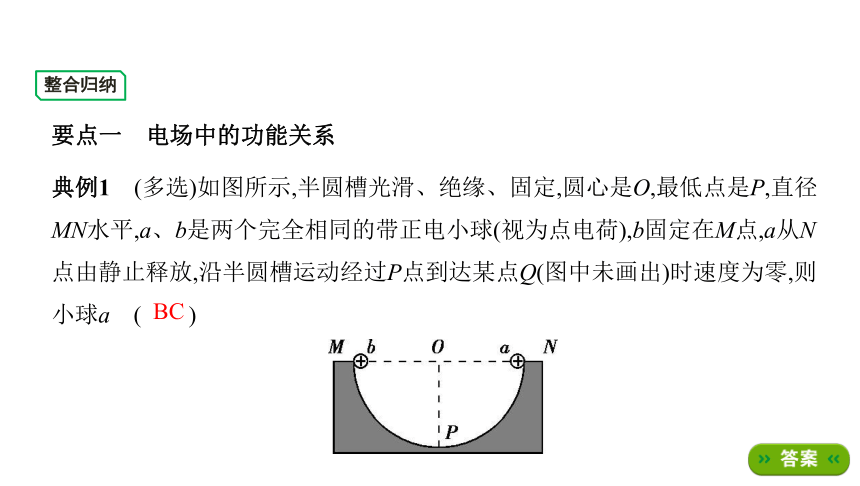
典例1????(多选)如图所示,半圆槽光滑、绝缘、固定,圆心是O,最低点是P,直径
MN水平,a、b是两个完全相同的带正电小球(视为点电荷),b固定在M点,a从N
点由静止释放,沿半圆槽运动经过P点到达某点Q(图中未画出)时速度为零,则
小球a?( )
BC
A.从N点到Q点的过程中,重力与库仑力的合力先增大后减小
B.从N点到P点的过程中,速率先增大后减小
C.从N点到Q点的过程中,电势能一直增加
D.从P点到Q点的过程中,动能减少量小于电势能增加量
解析 小球a从N点释放到达Q点的过程中,a、b两球的距离一直减小,库
仑力变大,a受重力不变,重力和库仑力的夹角从90°一直减小,故合力一直变
大,选项A错误;小球a从N到P的过程中,速度方向与重力和库仑力的合力方向
的夹角由小于90°到大于90°,故库仑力与重力的合力先做正功后做负功,a球
速率先增大后减小,选项B正确;小球a由N到Q的过程中库仑力一直做负功,电
势能一直增加,选项C正确;小球a从P到Q的过程中,减少的动能转化为重力势
能和电势能,故动能的减少量大于电势能的增加量,选项D错误。
整合归纳
1.功能关系
(1)若只有静电力做功,电势能与动能之和保持不变。
(2)若只有静电力和重力做功,电势能、重力势能、动能之和保持不变。
(3)除重力外,其他各力对物体做的功等于物体机械能的变化量。
(4)所有力对物体所做功的代数和,等于物体动能的变化量。
2.静电力做功的计算方法
(1)由公式W=Fl cos α计算,此公式只适用于匀强电场,可变形为:W=qEl cos
α。
(2)由W=qU计算,此公式适用于任何形式的静电场。
(3)由动能定理计算:W静电力+W其他力=ΔEk。
(4)由电势能的变化计算:WAB=?-?。
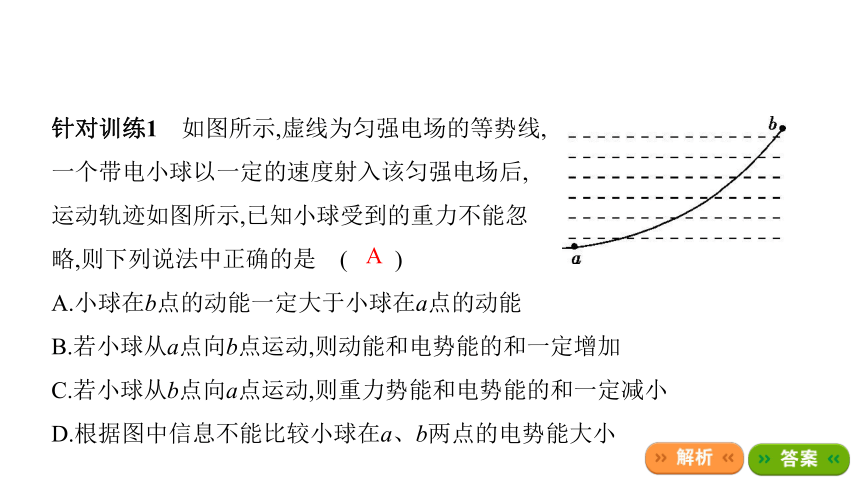
针对训练1 如图所示,虚线为匀强电场的等势线,
一个带电小球以一定的速度射入该匀强电场后,
运动轨迹如图所示,已知小球受到的重力不能忽
略,则下列说法中正确的是?( )
A.小球在b点的动能一定大于小球在a点的动能
B.若小球从a点向b点运动,则动能和电势能的和一定增加
C.若小球从b点向a点运动,则重力势能和电势能的和一定减小
D.根据图中信息不能比较小球在a、b两点的电势能大小
A
解析 由于等势线水平,则电场线一定沿竖直方向,根据曲线运动的轨迹与
合力的关系可知,小球受到的静电力一定竖直向上,且合力也竖直向上,由此
可知若小球从a点向b点运动,合力对小球做正功,故小球动能一定增加,若小
球从b点向a点运动,合力对小球做负功,故小球的动能减少,则选项A正确;小
球从a点向b点运动的过程中重力势能增加,根据能量守恒定律,可知动能和电
势能的和一定减小,则选项B错误;同理可知小球从b点向a点运动过程中动能
减小,则重力势能和电势能的和一定增加,则选项C错误;由于小球从a点向b点
运动过程中,静电力一定做正功,则电势能一定减小,故小球在a点的电势能一
定大于在b点的电势能,故选项D错误。
要点二 电场线、电势线(面)及带电粒子的运动轨迹问题
典例2 如图所示,真空中有一个固定的点电荷,电荷量为+Q。虚线表示该点
电荷产生的电场中的等势面。两个一价离子M、N(不计重力和它们之间的
相互作用力)先后从a点以相同的速率v0射入该电场,曲线apb为M离子的运动
轨迹,曲线aqc为N离子的运动轨迹,其中p、q分别是它们离固定点电荷最近的
位置。下列说法中正确的是?( )
B
A.M是正离子,N是负离子
B.M在p点的速率大于N在q点的速率
C.M在b点的速率大于N在c点的速率
D.M从p→b过程中电势能的增量等于N从a→q过程中电势能的增量
解析 由题图可知离子N受到中心电荷的斥力,而离子M受到中心电荷的引
力,故两离子的电性一定不同,由于中心电荷为正电荷,则M一定是负离子,N一
定是正离子,故A错误;由题图可知M离子从a→p的过程中,静电力做正功,动能
增加;而N离子从a→q的过程中,静电力做负功,动能减小,所以M在p点的速率
一定大于N在q点的速率,故B正确;a、b、c三点在同一等势面上,可知从a到b
和从a到c过程中静电力所做的总功为零,根据动能定理可知M在b点的速率等
于N在c点的速率,故C错误。由题图可知p、b间电势差的绝对值小于a、q间
电势差的绝对值,根据静电力做功W=Uq知,M从p→b过程中静电力做的功小
于N从a→q过程中静电力做的功,M从p→b过程中电势能的增量小于N从a→q
过程中电势能的增量,故D错误。
学法指导
1.等势面总是和电场线垂直,已知电场线可以画出等势面,已知等势面也可以
画出电场线。
2.带电粒子运动轨迹的分析
(1)判断速度方向:带电粒子运动轨迹上过某点的切线方向为粒子在该点处的
速度方向。
(2)判断静电力(或电场强度)的方向:仅受静电力作用时,带电粒子所受静电力
方向指向轨迹的凹侧,再根据粒子带电的正、负判断电场强度的方向。
(3)判断静电力做功的正、负及电势能的增减:若静电力与速度方向成锐角,
则静电力做正功,电势能减少;若静电力与速度方向成钝角,则静电力做负功,
电势能增加。
针对训练2????(多选)如图所示,实线是α粒子仅在静
电力作用下由a点运动到b点的运动轨迹,虚线可能
是电场线,也可能是等差等势线,则?( )
A.若虚线是电场线,则α粒子在a点的电势能大,动能小
B.若虚线是等差等势线,则α粒子在a点的电势能大,动能小
C.无论虚线是电场线还是等差等势线,a点的电势一定低于b点的电势
D.无论虚线是电场线还是等差等势线,α粒子在a点的加速度一定大于在b点
的加速度
BD
解析 若虚线是电场线,因为α粒子带正电荷,由其运动轨迹可知其受静电
力方向向左,则α粒子由a点运动到b点过程中,静电力做负功,动能减小,电势能
增大,故a点电势低于b点电势;若虚线是等差等势线,则电场线与虚线垂直指
向下方,则α粒子由a点运动到b点过程中,静电力做正功,动能增大,电势能减
小,故a点电势高于b点电势,B项正确,A、C项错误。无论虚线是电场线还是
等差等势线,均有Ea>Eb,则Fa>Fb,再结合牛顿第二定律可知α粒子在a点的加速
度一定大于在b点的加速度,D项正确。
要点三 带电粒子在交变电场中的运动
典例3 如图甲所示,A和B是真空中正对面积很大的平行金属板,O点是一个
可以连续产生粒子的粒子源,O点到A、B的距离都是l。现在A、B之间加上
电压,电压UAB随时间变化的规律如图乙所示。已知粒子源在交变电压的一个
周期内可以均匀产生300个粒子,粒子质量为m、电荷量为-q。这种粒子产生
后,在静电力作用下从静止开始运动。设粒子一旦碰到金属板,它就附在金属
板上不再运动,且电荷量同时消失,不影响A、B板间电压。不计粒子的重力,
不考虑粒子之间的相互作用力。已知上述物理量l=0.6 m,U0=1.2×103 V,T=1.2
×10-2 s,m=5×10-10 kg,q=1.0×10-7 C。
?
(1)在t=0时刻产生的粒子,会在什么时刻到达哪个极板?
(2)在t=0到t=?这段时间内哪个时刻产生的粒子刚好不能到达A板?
(3)在t=0到t=?这段时间内产生的粒子有多少个可到达A板?
解析 (1)根据题图乙可知,从t=0时刻开始,A板电势高于B板电势,粒子向A板
运动。因为x=??=3.6 m>l,所以粒子从t=0时刻开始,一直加速到达A
板。设粒子到达A板的时间为t,则l=??t2
解得t=?×10-3 s。
(2)在0~?时间内,粒子的加速度大小为a1=?=2×105 m/s2
在?~T时间内,粒子的加速度大小为a2=?=4×105 m/s2
可知a2=2a1,若粒子在0~?时间内加速Δt,再在?~T时间内减速?刚好不能到
答案 (1)?×10-3 s 到达A极板 (2)4×10-3 s (3)100个
达A板,则l=?a1Δt·?Δt
解得Δt=2×10-3 s
因为?=6×10-3 s,所以在0~?时间里4×10-3 s时刻产生的粒子刚好不能到达A
板。
(3)因为粒子源在一个周期内可以产生300个粒子,而在0~?时间内的前?时间
内产生的粒子可以到达A板,所以到达A板的粒子数n=300×?×?=100(个)。
典例4 在金属板A、B间加上如图乙所示的大小不变、方向周期性变化的
交变电压,其周期为T。现有电子以平行于金属板的速度v0从两板中央射入
(如图甲所示)。已知电子的质量为m,电荷量为e,不计电子的重力,求:
(1)若电子从t=0时刻射入,在半个周期内恰好能从A板的边缘飞出,则电子飞出时速度的大小为多少?
(2)若电子从t=0时刻射入,恰能平行于金属板飞出,则金属板至少为多长?
(3)若电子恰能从两板中央平行于金属板飞出,电子应从哪一时刻射入?两板
间距至少为多大?
答案 (1)? (2)v0T (3)?+k·?(k=0,1,2,…)????T?
解析 (1)由动能定理得:
e·?=?mv2-?m?
解得v=?。
(2)t=0时刻射入的电子,在垂直于极板方向上做匀加速运动,向正极板方向偏
转,半个周期后电场方向反向,则电子继续在该方向上做匀减速运动,再经过
半个周期,电场方向上的速度减到零,实际速度等于初速度v0,平行于极板,以
后继续重复这样的运动。
要使电子恰能平行于金属板飞出,则在OO'方向上至少运动一个周期,故金属
板长至少为L=v0T。
(3)若要使电子从极板中央平行于极板飞出,则电子在电场方向上应先加速、
再减速,反向加速再减速,每段时间相同,一个周期后恰好回到OO'。所以应在
t=?+k·?(k=0,1,2,…)时射入。
极板间距离要求满足在加速、减速阶段电子不打到极板上。设极板间距
为d。
由牛顿第二定律有a=?。
加速阶段运动的距离s=?·?·?≤?
可解得d≥T?
故两极板间距至少为T?。
学法指导
1.注重全面分析(分析受力特点和运动规律),抓住粒子的运动具有周期性和
在空间上具有对称性的特征,求解粒子运动过程中的速度、位移、做功或确
定与物理过程相关的边界条件。
2.分析时从两条思路出发:一是力和运动的关系,根据牛顿第二定律及运动学
规律分析;二是功能关系。
3.此类题型一般有三种情况:一是粒子做单向直线运动(一般用牛顿运动定律
求解),二是粒子做往返运动(一般分段研究),三是粒子做偏转运动(一般根据
交变电场的特点分段研究)。
针对训练3????(多选)如图甲所示,两平行金属板竖直放置,左极板接地,中间有
小孔,右极板电势随时间变化的规律如图乙所示,电子原来静止在左极板小孔
处,不计电子的重力,下列说法正确的是?( )
AC
A.若t=0时刻释放电子,电子始终向右运动,直到打到右极板上
B.若t=0时刻释放电子,电子可能在两板间做往返运动
C.若t=?时刻释放电子,电子可能在两板间做往返运动,也可能打到右极板上
D.若t=?时刻释放电子,电子必然打到左极板上
解析 若t=0时刻释放电子,电子将重复先加速后减速的运动,直到打到右
极板,不会在两板间做往返运动,所以A正确,B错误;若从t=?时刻释放电子,电
子先加速?,再减速?,电子可能已到达右极板,若此时未到达右极板,则电子
将在两极板间做往返运动,所以C正确;同理,若从t=?时刻释放电子,电子有
可能达到右极板,也有可能从左极板射出,这取决于两板间的距离,所以D项错
误。
针对训练4 如图甲所示,在y=0和y=2 m之间有沿着x轴方向的匀强电场,MN
为电场区域的上边界,在x轴方向范围足够大。电场强度的变化如图乙所示,
取x轴正方向为电场正方向,现有一个带负电的粒子,粒子的比荷为?=1.0×
10-2 C/kg,在t=0时刻以速度v0=5×102 m/s从O点沿y轴正方向进入电场区域,不计
粒子重力。求:
(1)粒子通过电场区域的时间;
(2)粒子离开电场时的位置坐标;
(3)粒子通过电场区域后沿x轴方向的速度大小。
答案 (1)4×10-3 s (2)(-2×10-5 m,2 m) (3)4×10-3 m/s
解析 (1)因粒子初速度方向垂直电场方向,在电场中做类平抛运动,所以粒
子通过电场区域的时间
t=?=4×10-3 s
(2)粒子沿x轴负方向先加速后减速,加速时的加速度大小为a1=?=4 m/s2,减
速时的加速度大小为a2=?=2 m/s2由运动学规律得
x轴方向上的位移为x=?a1?+a1?-?a2?=2×10-5 m
因此粒子离开电场时的位置坐标为(-2×10-5 m,2 m)
(3)粒子通过电场区域后沿x轴方向的速度为vx=a1?-a2?=4×10-3 m/s
章末总结
要点一 电场中的功能关系
整合归纳
典例1????(多选)如图所示,半圆槽光滑、绝缘、固定,圆心是O,最低点是P,直径
MN水平,a、b是两个完全相同的带正电小球(视为点电荷),b固定在M点,a从N
点由静止释放,沿半圆槽运动经过P点到达某点Q(图中未画出)时速度为零,则
小球a?( )
BC
A.从N点到Q点的过程中,重力与库仑力的合力先增大后减小
B.从N点到P点的过程中,速率先增大后减小
C.从N点到Q点的过程中,电势能一直增加
D.从P点到Q点的过程中,动能减少量小于电势能增加量
解析 小球a从N点释放到达Q点的过程中,a、b两球的距离一直减小,库
仑力变大,a受重力不变,重力和库仑力的夹角从90°一直减小,故合力一直变
大,选项A错误;小球a从N到P的过程中,速度方向与重力和库仑力的合力方向
的夹角由小于90°到大于90°,故库仑力与重力的合力先做正功后做负功,a球
速率先增大后减小,选项B正确;小球a由N到Q的过程中库仑力一直做负功,电
势能一直增加,选项C正确;小球a从P到Q的过程中,减少的动能转化为重力势
能和电势能,故动能的减少量大于电势能的增加量,选项D错误。
整合归纳
1.功能关系
(1)若只有静电力做功,电势能与动能之和保持不变。
(2)若只有静电力和重力做功,电势能、重力势能、动能之和保持不变。
(3)除重力外,其他各力对物体做的功等于物体机械能的变化量。
(4)所有力对物体所做功的代数和,等于物体动能的变化量。
2.静电力做功的计算方法
(1)由公式W=Fl cos α计算,此公式只适用于匀强电场,可变形为:W=qEl cos
α。
(2)由W=qU计算,此公式适用于任何形式的静电场。
(3)由动能定理计算:W静电力+W其他力=ΔEk。
(4)由电势能的变化计算:WAB=?-?。
针对训练1 如图所示,虚线为匀强电场的等势线,
一个带电小球以一定的速度射入该匀强电场后,
运动轨迹如图所示,已知小球受到的重力不能忽
略,则下列说法中正确的是?( )
A.小球在b点的动能一定大于小球在a点的动能
B.若小球从a点向b点运动,则动能和电势能的和一定增加
C.若小球从b点向a点运动,则重力势能和电势能的和一定减小
D.根据图中信息不能比较小球在a、b两点的电势能大小
A
解析 由于等势线水平,则电场线一定沿竖直方向,根据曲线运动的轨迹与
合力的关系可知,小球受到的静电力一定竖直向上,且合力也竖直向上,由此
可知若小球从a点向b点运动,合力对小球做正功,故小球动能一定增加,若小
球从b点向a点运动,合力对小球做负功,故小球的动能减少,则选项A正确;小
球从a点向b点运动的过程中重力势能增加,根据能量守恒定律,可知动能和电
势能的和一定减小,则选项B错误;同理可知小球从b点向a点运动过程中动能
减小,则重力势能和电势能的和一定增加,则选项C错误;由于小球从a点向b点
运动过程中,静电力一定做正功,则电势能一定减小,故小球在a点的电势能一
定大于在b点的电势能,故选项D错误。
要点二 电场线、电势线(面)及带电粒子的运动轨迹问题
典例2 如图所示,真空中有一个固定的点电荷,电荷量为+Q。虚线表示该点
电荷产生的电场中的等势面。两个一价离子M、N(不计重力和它们之间的
相互作用力)先后从a点以相同的速率v0射入该电场,曲线apb为M离子的运动
轨迹,曲线aqc为N离子的运动轨迹,其中p、q分别是它们离固定点电荷最近的
位置。下列说法中正确的是?( )
B
A.M是正离子,N是负离子
B.M在p点的速率大于N在q点的速率
C.M在b点的速率大于N在c点的速率
D.M从p→b过程中电势能的增量等于N从a→q过程中电势能的增量
解析 由题图可知离子N受到中心电荷的斥力,而离子M受到中心电荷的引
力,故两离子的电性一定不同,由于中心电荷为正电荷,则M一定是负离子,N一
定是正离子,故A错误;由题图可知M离子从a→p的过程中,静电力做正功,动能
增加;而N离子从a→q的过程中,静电力做负功,动能减小,所以M在p点的速率
一定大于N在q点的速率,故B正确;a、b、c三点在同一等势面上,可知从a到b
和从a到c过程中静电力所做的总功为零,根据动能定理可知M在b点的速率等
于N在c点的速率,故C错误。由题图可知p、b间电势差的绝对值小于a、q间
电势差的绝对值,根据静电力做功W=Uq知,M从p→b过程中静电力做的功小
于N从a→q过程中静电力做的功,M从p→b过程中电势能的增量小于N从a→q
过程中电势能的增量,故D错误。
学法指导
1.等势面总是和电场线垂直,已知电场线可以画出等势面,已知等势面也可以
画出电场线。
2.带电粒子运动轨迹的分析
(1)判断速度方向:带电粒子运动轨迹上过某点的切线方向为粒子在该点处的
速度方向。
(2)判断静电力(或电场强度)的方向:仅受静电力作用时,带电粒子所受静电力
方向指向轨迹的凹侧,再根据粒子带电的正、负判断电场强度的方向。
(3)判断静电力做功的正、负及电势能的增减:若静电力与速度方向成锐角,
则静电力做正功,电势能减少;若静电力与速度方向成钝角,则静电力做负功,
电势能增加。
针对训练2????(多选)如图所示,实线是α粒子仅在静
电力作用下由a点运动到b点的运动轨迹,虚线可能
是电场线,也可能是等差等势线,则?( )
A.若虚线是电场线,则α粒子在a点的电势能大,动能小
B.若虚线是等差等势线,则α粒子在a点的电势能大,动能小
C.无论虚线是电场线还是等差等势线,a点的电势一定低于b点的电势
D.无论虚线是电场线还是等差等势线,α粒子在a点的加速度一定大于在b点
的加速度
BD
解析 若虚线是电场线,因为α粒子带正电荷,由其运动轨迹可知其受静电
力方向向左,则α粒子由a点运动到b点过程中,静电力做负功,动能减小,电势能
增大,故a点电势低于b点电势;若虚线是等差等势线,则电场线与虚线垂直指
向下方,则α粒子由a点运动到b点过程中,静电力做正功,动能增大,电势能减
小,故a点电势高于b点电势,B项正确,A、C项错误。无论虚线是电场线还是
等差等势线,均有Ea>Eb,则Fa>Fb,再结合牛顿第二定律可知α粒子在a点的加速
度一定大于在b点的加速度,D项正确。
要点三 带电粒子在交变电场中的运动
典例3 如图甲所示,A和B是真空中正对面积很大的平行金属板,O点是一个
可以连续产生粒子的粒子源,O点到A、B的距离都是l。现在A、B之间加上
电压,电压UAB随时间变化的规律如图乙所示。已知粒子源在交变电压的一个
周期内可以均匀产生300个粒子,粒子质量为m、电荷量为-q。这种粒子产生
后,在静电力作用下从静止开始运动。设粒子一旦碰到金属板,它就附在金属
板上不再运动,且电荷量同时消失,不影响A、B板间电压。不计粒子的重力,
不考虑粒子之间的相互作用力。已知上述物理量l=0.6 m,U0=1.2×103 V,T=1.2
×10-2 s,m=5×10-10 kg,q=1.0×10-7 C。
?
(1)在t=0时刻产生的粒子,会在什么时刻到达哪个极板?
(2)在t=0到t=?这段时间内哪个时刻产生的粒子刚好不能到达A板?
(3)在t=0到t=?这段时间内产生的粒子有多少个可到达A板?
解析 (1)根据题图乙可知,从t=0时刻开始,A板电势高于B板电势,粒子向A板
运动。因为x=??=3.6 m>l,所以粒子从t=0时刻开始,一直加速到达A
板。设粒子到达A板的时间为t,则l=??t2
解得t=?×10-3 s。
(2)在0~?时间内,粒子的加速度大小为a1=?=2×105 m/s2
在?~T时间内,粒子的加速度大小为a2=?=4×105 m/s2
可知a2=2a1,若粒子在0~?时间内加速Δt,再在?~T时间内减速?刚好不能到
答案 (1)?×10-3 s 到达A极板 (2)4×10-3 s (3)100个
达A板,则l=?a1Δt·?Δt
解得Δt=2×10-3 s
因为?=6×10-3 s,所以在0~?时间里4×10-3 s时刻产生的粒子刚好不能到达A
板。
(3)因为粒子源在一个周期内可以产生300个粒子,而在0~?时间内的前?时间
内产生的粒子可以到达A板,所以到达A板的粒子数n=300×?×?=100(个)。
典例4 在金属板A、B间加上如图乙所示的大小不变、方向周期性变化的
交变电压,其周期为T。现有电子以平行于金属板的速度v0从两板中央射入
(如图甲所示)。已知电子的质量为m,电荷量为e,不计电子的重力,求:
(1)若电子从t=0时刻射入,在半个周期内恰好能从A板的边缘飞出,则电子飞出时速度的大小为多少?
(2)若电子从t=0时刻射入,恰能平行于金属板飞出,则金属板至少为多长?
(3)若电子恰能从两板中央平行于金属板飞出,电子应从哪一时刻射入?两板
间距至少为多大?
答案 (1)? (2)v0T (3)?+k·?(k=0,1,2,…)????T?
解析 (1)由动能定理得:
e·?=?mv2-?m?
解得v=?。
(2)t=0时刻射入的电子,在垂直于极板方向上做匀加速运动,向正极板方向偏
转,半个周期后电场方向反向,则电子继续在该方向上做匀减速运动,再经过
半个周期,电场方向上的速度减到零,实际速度等于初速度v0,平行于极板,以
后继续重复这样的运动。
要使电子恰能平行于金属板飞出,则在OO'方向上至少运动一个周期,故金属
板长至少为L=v0T。
(3)若要使电子从极板中央平行于极板飞出,则电子在电场方向上应先加速、
再减速,反向加速再减速,每段时间相同,一个周期后恰好回到OO'。所以应在
t=?+k·?(k=0,1,2,…)时射入。
极板间距离要求满足在加速、减速阶段电子不打到极板上。设极板间距
为d。
由牛顿第二定律有a=?。
加速阶段运动的距离s=?·?·?≤?
可解得d≥T?
故两极板间距至少为T?。
学法指导
1.注重全面分析(分析受力特点和运动规律),抓住粒子的运动具有周期性和
在空间上具有对称性的特征,求解粒子运动过程中的速度、位移、做功或确
定与物理过程相关的边界条件。
2.分析时从两条思路出发:一是力和运动的关系,根据牛顿第二定律及运动学
规律分析;二是功能关系。
3.此类题型一般有三种情况:一是粒子做单向直线运动(一般用牛顿运动定律
求解),二是粒子做往返运动(一般分段研究),三是粒子做偏转运动(一般根据
交变电场的特点分段研究)。
针对训练3????(多选)如图甲所示,两平行金属板竖直放置,左极板接地,中间有
小孔,右极板电势随时间变化的规律如图乙所示,电子原来静止在左极板小孔
处,不计电子的重力,下列说法正确的是?( )
AC
A.若t=0时刻释放电子,电子始终向右运动,直到打到右极板上
B.若t=0时刻释放电子,电子可能在两板间做往返运动
C.若t=?时刻释放电子,电子可能在两板间做往返运动,也可能打到右极板上
D.若t=?时刻释放电子,电子必然打到左极板上
解析 若t=0时刻释放电子,电子将重复先加速后减速的运动,直到打到右
极板,不会在两板间做往返运动,所以A正确,B错误;若从t=?时刻释放电子,电
子先加速?,再减速?,电子可能已到达右极板,若此时未到达右极板,则电子
将在两极板间做往返运动,所以C正确;同理,若从t=?时刻释放电子,电子有
可能达到右极板,也有可能从左极板射出,这取决于两板间的距离,所以D项错
误。
针对训练4 如图甲所示,在y=0和y=2 m之间有沿着x轴方向的匀强电场,MN
为电场区域的上边界,在x轴方向范围足够大。电场强度的变化如图乙所示,
取x轴正方向为电场正方向,现有一个带负电的粒子,粒子的比荷为?=1.0×
10-2 C/kg,在t=0时刻以速度v0=5×102 m/s从O点沿y轴正方向进入电场区域,不计
粒子重力。求:
(1)粒子通过电场区域的时间;
(2)粒子离开电场时的位置坐标;
(3)粒子通过电场区域后沿x轴方向的速度大小。
答案 (1)4×10-3 s (2)(-2×10-5 m,2 m) (3)4×10-3 m/s
解析 (1)因粒子初速度方向垂直电场方向,在电场中做类平抛运动,所以粒
子通过电场区域的时间
t=?=4×10-3 s
(2)粒子沿x轴负方向先加速后减速,加速时的加速度大小为a1=?=4 m/s2,减
速时的加速度大小为a2=?=2 m/s2由运动学规律得
x轴方向上的位移为x=?a1?+a1?-?a2?=2×10-5 m
因此粒子离开电场时的位置坐标为(-2×10-5 m,2 m)
(3)粒子通过电场区域后沿x轴方向的速度为vx=a1?-a2?=4×10-3 m/s
同课章节目录
- 第1章 静电力与电场强度
- 第1节 静电的产生及其微观解释
- 第2节 库仑定律
- 第3节 电场与电场强度
- 第4节 点电荷的电场 匀强电场
- 第5节 静电的利用与防护
- 第2章 电势能与电势差
- 第1节 静电力做功与电势能
- 第2节 电势与等势面
- 第3节 电势差与电场强度的关系
- 第4节 带电粒子在电场中的运动
- 第5节 科学探究:电容器
- 第3章 恒定电流
- 第1节 电流
- 第2节 电阻
- 第3节 电功与电热
- 第4节 串联电路和并联电路
- 第5节 科学测量:长度的测量及测量工具的选用
- 第6节 科学测量:金属丝的电阻率
- 第4章 闭合电路欧姆定律与科学用电
- 第1节 闭合电路欧姆定律
- 第2节 科学测量:电源的电动势和内阻
- 第3节 科学测量:用多用电表测量电学量
- 第4节 科学用电
- 第5章 初识电磁场与电磁波
- 第1节 磁场及其描述
- 第2节 电磁感应现象及其应用
- 第3节 初识电磁波及其应用
- 第4节 初识光量子与量子世界
- 第6章 能源与可持续发展
- 第1节 能量的多种形式
- 第2节 能量的转化与守恒
- 第3节 珍惜大自然
