第一章三角形的证明单元测试卷(Word版 含答案)
文档属性
| 名称 | 第一章三角形的证明单元测试卷(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 289.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 19:35:37 | ||
图片预览



文档简介
第一章 三角形的证明单元测试卷
一、选择题(共10小题,3*10=30)
1.满足下列条件的三角形不是直角三角形的是( )
A.三个内角之比为3∶4∶5
B.三边之比为3∶4∶5
C.三个内角之比为1∶2∶3
D.三边之比为1∶2∶
2.如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )
A.44° B.60° C.67° D.77°
3.如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
4.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD B.AC=BC
C.∠ABC=∠ABD D.∠BAC=∠BAD
5.如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是( )
A.30° B.35° C.40° D.45°
6. 如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )
A.40° B.36° C.30° D.25°
7. 如图,轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处测得灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )
A.45海里 B.35海里
C.50海里 D.25海里
8.已知∠AOB=30°,点P在∠AOB内部,P1与P关于OB对称,P2与P关于OA对称,则P1,O,P2三点所构成的三角形是( )
A.直角三角形 B. 钝角三角形
C.等腰三角形 D.等边三角形
9.如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E,若AC=3,BC=4,则DE等于( )
A.2 B. C. D.
10.如图,△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F. 下列结论:①∠BAD=∠CAD;②AD上任意一点到AB,AC的距离相等;③BD=CD;④若点P在直线AD上,则PB=PC.其中正确的是( )
A.① B.①② C.①②③ D.①②③④
二.填空题(共8小题,3*8=24)
11. 已知:在△ABC中,AB≠AC,求证:∠B≠∠C.若用反证法来证明这个结论,可以假设__________.
12. “垂直于同一条直线的两条直线互相平行”的逆命题是__ __(填“真”或“假”)命题.
13. 如图,已知点B,C,F,E在同一条直线上,∠1=∠2,BC=EF,要使△ABC≌△DEF,还需添加一个条件,这个条件可以是_________________.(只需写出一个)
14.如图,在△ABC中,高AD,CE相交于点H,且CH=AB,则∠ACB=________.
15. 如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,点E为AD边上一点,连接BD,CE,CE与BD交于点F,且CE∥AB,若AB=8,CE=6,则BC的长为________.
16.在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,连接AD,若△ABD为直角三角形,则∠ADC的度数为______________
17.如图,圆柱形容器的高为1.2 m,底面周长为1 m,在容器内壁离容器底部0.3 m的点B处有一只蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3 m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为_________.(容器厚度忽略不计)
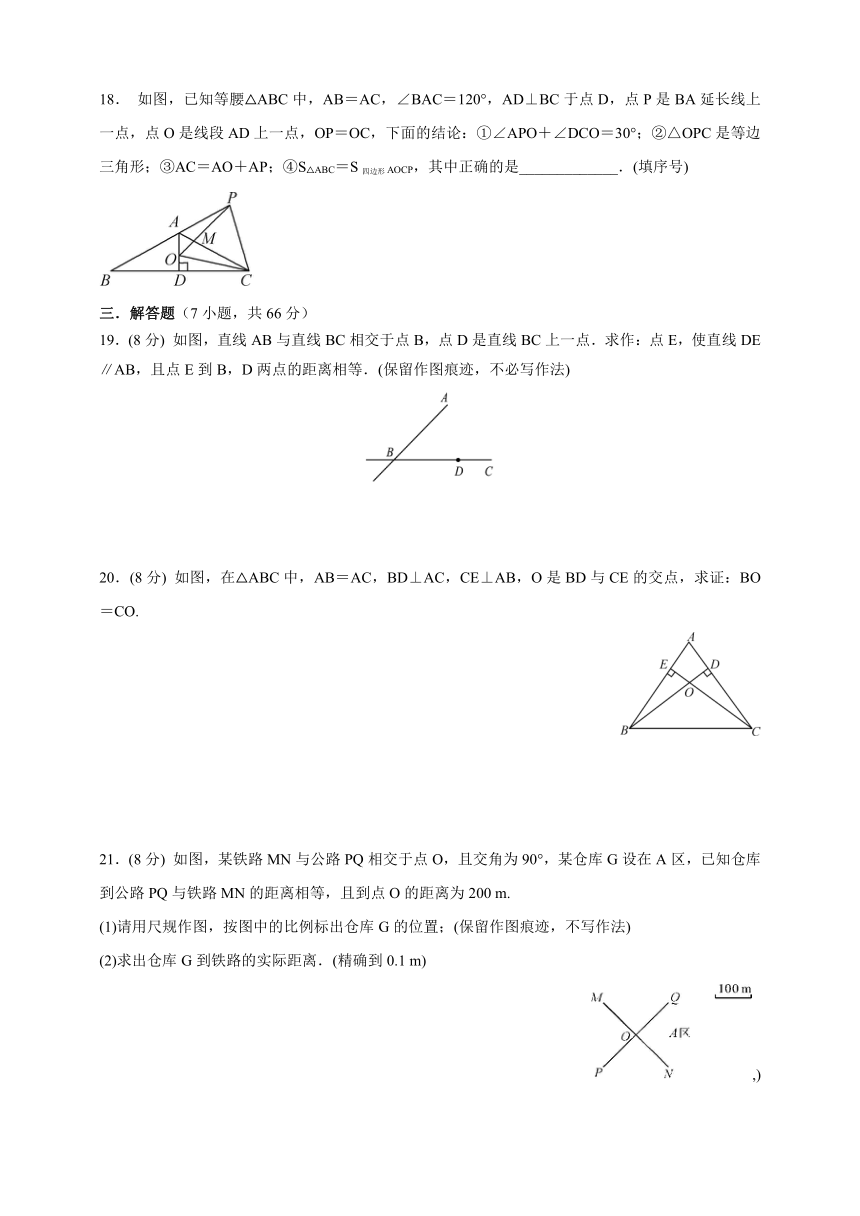
18. 如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP,其中正确的是_____________.(填序号)
三.解答题(7小题,共66分)
19.(8分) 如图,直线AB与直线BC相交于点B,点D是直线BC上一点.求作:点E,使直线DE∥AB,且点E到B,D两点的距离相等.(保留作图痕迹,不必写作法)
20.(8分) 如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,O是BD与CE的交点,求证:BO=CO.
21.(8分) 如图,某铁路MN与公路PQ相交于点O,且交角为90°,某仓库G设在A区,已知仓库到公路PQ与铁路MN的距离相等,且到点O的距离为200 m.
(1)请用尺规作图,按图中的比例标出仓库G的位置;(保留作图痕迹,不写作法)
(2)求出仓库G到铁路的实际距离.(精确到0.1 m)
,)
22.(10分) 如图,已知△ABC是边长为6 cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速运动,其中点P运动的速度是1 cm/s,点Q运动的速度是2 cm/s,当点Q到达点C时,P,Q两点都停止运动,设运动时间为t s,解答下列问题:
(1)当点Q到达点C时,PQ与AB的位置关系如何?请说明理由.
(2)在点P与点Q的运动过程中,△BPQ是否能成为等边三角形?若能,请求出t;若不能,请说明理由.
23.(10分) 如图,在Rt△ABC中,∠C=90°,∠A=30°.
(1)作线段AB的垂直平分线DE,垂足为点E,交AC于点D,要求用尺规作图,保留作图痕迹,标注有关字母,不要求写作法和证明;
(2)连接BD,求∠CBD的度数;
(3)如果△BCD的面积为4,请求出△BAD的面积.
24.(10分) 如图,在△ABC中,∠ABC=45°,DH垂直平分BC交AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F.求证:
(1)BF=AC;
(2)CE=BF.
25.(12分) 如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形APQ.
(1)求点B的坐标.
(2)在点P运动过程中,∠ABQ的大小是否发生改变?若不改变,求出其大小;若改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求点P的坐标.
参考答案
1-5 ACAAC 6-10BDDCD
11.∠B=∠C 12.真 13.AC=DF(答案不唯一) 14.45° 15.2 16. 130°或90°
17. 1.3m 18. ①②③④
19.解:图略,过点D作∠CDF=∠CBA,延长FD交线段BD的垂直平分线于点E,则DE∥AB,且点E到B,D两点的距离相等.
20. 证明:∵AB=AC,∴∠ABC=∠ACB. ∵BD⊥AC,CE⊥AB,∴∠BDC=∠CEB=90°,在△BCE和△CBD中,∴△BCE≌△CBD(AAS), ∴∠BCE=∠CBD,∴BO=CO.
21. 解:(1)仓库G的位置如图所示.
(2)过点G作DG⊥MN,垂足为D.由(1)得,OG平分∠QON. ∵∠QON=90°,∴∠OGD=∠GOD=45°. ∴OD=DG.∵DO2+DG2=40 000,解得OD=DG=100≈141.4 m. ∴仓库到铁路的实际距离约为141.4 m.
22.解:(1)当点Q到达点C时,PQ与AB垂直.理由:∵点Q到达点C时,BQ=BC=6 cm,∴t==3. ∴AP=3 cm. ∴BP=AB-AP=3 cm=AP. ∴点P为AB的中点.∴PQ⊥AB.
(2)能.∵∠B=60°,∴当BP=BQ时,△BPQ为等边三角形.∴6-t=2t,解得t=2. ∴当t=2时,△BPQ是等边三角形.
23. 解:(1)如图,DE为所作. (2)∵DE垂直平分AB, ∴DA=DB, ∴∠DBA=∠A=30°, ∵∠ABC=90°-∠A=60°,∴∠CBD=∠ABC-∠DBA=60°-30°=30°.(3)在Rt△BCD中,∵∠CBD=30°,∴DB=2CD, 而DA=DB, ∴DA=2CD,∴S△ABD=2S△BCD=8.
24. 解:(1)∵DH垂直平分BC,∴BD=DC,∴∠ABC=∠DCB=45°,∴∠BDC=180°-45°-45°=90°,∴∠ADC=90°,∴∠ABE+∠A=∠ACD+∠A=90°,∴∠ABE=∠ACD,∴△BDF≌△CDA(ASA),∴BF=AC.(2)∵BE平分∠ABC,∴∠ABE=∠CBE,又∵BE⊥AC,∴∠AEB=∠CEB=90°,又∵BE=BE,∴△ABE≌△CBE(ASA),∴CE=AE=AC,又∵AC=BF,∴CE=BF.
25.解:(1)如图①,过点B作BC⊥x轴于点C. ∵△AOB为等边三角形,且OA=2,∴∠AOB=60°,BO=OA=2. ∴∠BOC=30°. 又∵∠OCB=90°, ∴BC=OB=1,∴OC=. ∴点B的坐标为(,1).
(2)∠ABQ的大小始终不变.∵△APQ,△AOB均为等边三角形,∴AP=AQ,AO=AB,∠PAQ=∠OAB=60°. ∴∠PAO=∠QAB. 在△APO与△AQB中,
∴△APO≌△AQB(SAS).∴∠ABQ=∠AOP=90°.
(3)如图②,当OQ∥AB时点P在x轴的负半轴上,点Q在点B的下方,∵AB∥OQ,∴∠BQO=180°-∠ABQ=90°,∠BOQ=∠ABO=60°. ∴∠OBQ=30°. 又OB=OA=2,
∴OQ=OB=1,∴BQ=. 由(2)可知,△APO≌△AQB,∴OP=BQ=. ∴此时点P的坐标为(-,0).
一、选择题(共10小题,3*10=30)
1.满足下列条件的三角形不是直角三角形的是( )
A.三个内角之比为3∶4∶5
B.三边之比为3∶4∶5
C.三个内角之比为1∶2∶3
D.三边之比为1∶2∶
2.如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠BDC等于( )
A.44° B.60° C.67° D.77°
3.如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
4.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD B.AC=BC
C.∠ABC=∠ABD D.∠BAC=∠BAD
5.如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是( )
A.30° B.35° C.40° D.45°
6. 如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )
A.40° B.36° C.30° D.25°
7. 如图,轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处测得灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )
A.45海里 B.35海里
C.50海里 D.25海里
8.已知∠AOB=30°,点P在∠AOB内部,P1与P关于OB对称,P2与P关于OA对称,则P1,O,P2三点所构成的三角形是( )
A.直角三角形 B. 钝角三角形
C.等腰三角形 D.等边三角形
9.如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E,若AC=3,BC=4,则DE等于( )
A.2 B. C. D.
10.如图,△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F. 下列结论:①∠BAD=∠CAD;②AD上任意一点到AB,AC的距离相等;③BD=CD;④若点P在直线AD上,则PB=PC.其中正确的是( )
A.① B.①② C.①②③ D.①②③④
二.填空题(共8小题,3*8=24)
11. 已知:在△ABC中,AB≠AC,求证:∠B≠∠C.若用反证法来证明这个结论,可以假设__________.
12. “垂直于同一条直线的两条直线互相平行”的逆命题是__ __(填“真”或“假”)命题.
13. 如图,已知点B,C,F,E在同一条直线上,∠1=∠2,BC=EF,要使△ABC≌△DEF,还需添加一个条件,这个条件可以是_________________.(只需写出一个)
14.如图,在△ABC中,高AD,CE相交于点H,且CH=AB,则∠ACB=________.
15. 如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,点E为AD边上一点,连接BD,CE,CE与BD交于点F,且CE∥AB,若AB=8,CE=6,则BC的长为________.
16.在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,连接AD,若△ABD为直角三角形,则∠ADC的度数为______________
17.如图,圆柱形容器的高为1.2 m,底面周长为1 m,在容器内壁离容器底部0.3 m的点B处有一只蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3 m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为_________.(容器厚度忽略不计)
18. 如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP,其中正确的是_____________.(填序号)
三.解答题(7小题,共66分)
19.(8分) 如图,直线AB与直线BC相交于点B,点D是直线BC上一点.求作:点E,使直线DE∥AB,且点E到B,D两点的距离相等.(保留作图痕迹,不必写作法)
20.(8分) 如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,O是BD与CE的交点,求证:BO=CO.
21.(8分) 如图,某铁路MN与公路PQ相交于点O,且交角为90°,某仓库G设在A区,已知仓库到公路PQ与铁路MN的距离相等,且到点O的距离为200 m.
(1)请用尺规作图,按图中的比例标出仓库G的位置;(保留作图痕迹,不写作法)
(2)求出仓库G到铁路的实际距离.(精确到0.1 m)
,)
22.(10分) 如图,已知△ABC是边长为6 cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速运动,其中点P运动的速度是1 cm/s,点Q运动的速度是2 cm/s,当点Q到达点C时,P,Q两点都停止运动,设运动时间为t s,解答下列问题:
(1)当点Q到达点C时,PQ与AB的位置关系如何?请说明理由.
(2)在点P与点Q的运动过程中,△BPQ是否能成为等边三角形?若能,请求出t;若不能,请说明理由.
23.(10分) 如图,在Rt△ABC中,∠C=90°,∠A=30°.
(1)作线段AB的垂直平分线DE,垂足为点E,交AC于点D,要求用尺规作图,保留作图痕迹,标注有关字母,不要求写作法和证明;
(2)连接BD,求∠CBD的度数;
(3)如果△BCD的面积为4,请求出△BAD的面积.
24.(10分) 如图,在△ABC中,∠ABC=45°,DH垂直平分BC交AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F.求证:
(1)BF=AC;
(2)CE=BF.
25.(12分) 如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形APQ.
(1)求点B的坐标.
(2)在点P运动过程中,∠ABQ的大小是否发生改变?若不改变,求出其大小;若改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求点P的坐标.
参考答案
1-5 ACAAC 6-10BDDCD
11.∠B=∠C 12.真 13.AC=DF(答案不唯一) 14.45° 15.2 16. 130°或90°
17. 1.3m 18. ①②③④
19.解:图略,过点D作∠CDF=∠CBA,延长FD交线段BD的垂直平分线于点E,则DE∥AB,且点E到B,D两点的距离相等.
20. 证明:∵AB=AC,∴∠ABC=∠ACB. ∵BD⊥AC,CE⊥AB,∴∠BDC=∠CEB=90°,在△BCE和△CBD中,∴△BCE≌△CBD(AAS), ∴∠BCE=∠CBD,∴BO=CO.
21. 解:(1)仓库G的位置如图所示.
(2)过点G作DG⊥MN,垂足为D.由(1)得,OG平分∠QON. ∵∠QON=90°,∴∠OGD=∠GOD=45°. ∴OD=DG.∵DO2+DG2=40 000,解得OD=DG=100≈141.4 m. ∴仓库到铁路的实际距离约为141.4 m.
22.解:(1)当点Q到达点C时,PQ与AB垂直.理由:∵点Q到达点C时,BQ=BC=6 cm,∴t==3. ∴AP=3 cm. ∴BP=AB-AP=3 cm=AP. ∴点P为AB的中点.∴PQ⊥AB.
(2)能.∵∠B=60°,∴当BP=BQ时,△BPQ为等边三角形.∴6-t=2t,解得t=2. ∴当t=2时,△BPQ是等边三角形.
23. 解:(1)如图,DE为所作. (2)∵DE垂直平分AB, ∴DA=DB, ∴∠DBA=∠A=30°, ∵∠ABC=90°-∠A=60°,∴∠CBD=∠ABC-∠DBA=60°-30°=30°.(3)在Rt△BCD中,∵∠CBD=30°,∴DB=2CD, 而DA=DB, ∴DA=2CD,∴S△ABD=2S△BCD=8.
24. 解:(1)∵DH垂直平分BC,∴BD=DC,∴∠ABC=∠DCB=45°,∴∠BDC=180°-45°-45°=90°,∴∠ADC=90°,∴∠ABE+∠A=∠ACD+∠A=90°,∴∠ABE=∠ACD,∴△BDF≌△CDA(ASA),∴BF=AC.(2)∵BE平分∠ABC,∴∠ABE=∠CBE,又∵BE⊥AC,∴∠AEB=∠CEB=90°,又∵BE=BE,∴△ABE≌△CBE(ASA),∴CE=AE=AC,又∵AC=BF,∴CE=BF.
25.解:(1)如图①,过点B作BC⊥x轴于点C. ∵△AOB为等边三角形,且OA=2,∴∠AOB=60°,BO=OA=2. ∴∠BOC=30°. 又∵∠OCB=90°, ∴BC=OB=1,∴OC=. ∴点B的坐标为(,1).
(2)∠ABQ的大小始终不变.∵△APQ,△AOB均为等边三角形,∴AP=AQ,AO=AB,∠PAQ=∠OAB=60°. ∴∠PAO=∠QAB. 在△APO与△AQB中,
∴△APO≌△AQB(SAS).∴∠ABQ=∠AOP=90°.
(3)如图②,当OQ∥AB时点P在x轴的负半轴上,点Q在点B的下方,∵AB∥OQ,∴∠BQO=180°-∠ABQ=90°,∠BOQ=∠ABO=60°. ∴∠OBQ=30°. 又OB=OA=2,
∴OQ=OB=1,∴BQ=. 由(2)可知,△APO≌△AQB,∴OP=BQ=. ∴此时点P的坐标为(-,0).
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
