18.2.3正方形的性质与判定同步练习(Word版 含答案)
文档属性
| 名称 | 18.2.3正方形的性质与判定同步练习(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 875.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 19:46:29 | ||
图片预览

文档简介
18.2.3正方形的性质与判定
一、选择题
1、下列说法不正确的是( )
A.一组同旁内角相等的平行四边形是矩形 B.一组邻边相等的菱形是正方形
C.有三个角是直角的四边形是矩形 D.对角线相等的菱形是正方形
2、已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.①② B.②③ C.①③ D.②④
3、如图,已知P是正方形ABCD的对角线BD上一点,且BP=BC,则∠BCP的度数是( )
A.45° B.22.5° C.67.5° D.75°
4、如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为( )
A.45° B.55° C.60° D.75°
5、如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.4 B.2 C. D.2
6、如图,有一个平行四边形ABCD和一个正方形CEFG,其中点E在边AD上.若∠ECD=43°,∠AEF=28°,则∠B的度数为( )
A.55° B.75° C.65° D.60°
7、如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为( )
A.(1,2.5) B.(1,1+) C.(1,3) D.(﹣1,1+)
8、如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E;PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,
正确的有( )个.
A.5 B.4 C.3 D.2
9、如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:
①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的是( )
A.①③ B.①②③④ C.①②③ D.①③④
10、已知:如图,在正方形ABCD外取一点E, 连接AE、BE、DE.过点A作AE的垂线交DE 于点P.
若AE=AP=1,PB=.下列结论:①APD≌△AEB;②点B到直线AE的距离为;③EB⊥ED;④S△APD+S△APB=1+;⑤S正方形ABCD=4+. 其中正确结论的序号是( )
A.①③④ B.①②⑤ C.①③④ D.①③⑤
二、填空题
11、如图,在正方形ABCD中,E是对角线BD上一点,AE的延长线交CD于点F,连接CE.若∠BAE=56°,则∠CEF= °.
12、如图,三个边长均为2的正方形重叠在一起,O1,O2是其中两个正方形的中心,
则阴影部分的面积是 ?
13、四边形ABCD的对角线AC和BD相交于点O,设有下列条件:①AB=AD;②∠DAB=90°;
③AO=CO,BO=DO;④矩形ABCD;⑤菱形ABCD,⑥正方形ABCD,
则在下列推理不成立的是
A、①④?⑥; B、①③?⑤; C、①②?⑥; D、②③?④
14、如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,
则正方形ABCD的边长为_____.
15、如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,
那么CH的长是 .
16、如图,在正方形ABCD的各边上顺次截取AE=BF=CG=DH=3,若四边形EFGH面积是10,
则正方形ABCD的面积为 .
17、如图,正方形ABCD的边长为2,E为边BC的中点,点P在对角线BD上移动,
则PE+PC的最小值是 .?
18、如图,以的斜边为边,向外作正方形,设正方形的对角线与的交点为O,连接,若,,则的值是__________.
19、已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
20、如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,
下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.
其中正确结论有( )个.
A.2 B.3 C.4 D.5
三、解答题
21、正方形中,对角线、交于点O,E为上一点,延长到点N,使,连接、.
(1)求证:为直角三角形.
(2)若,正方形的边长为6,求的长.
22、如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
23、如图,在△ABC中,AC=BC=6,∠ACB>90°,∠ABC的平分线交AC于点D,E是AB上点,且BE=BC,CF∥ED交BD于点F,连接EF,ED.
(1)求证:四边形CDEF是菱形;
(2)当∠ACB= 度时,四边形CDEF是正方形,请给予证明;并求此时正方形的边长.
24、如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
25、如图,正方形ABCD的对角线AC、BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)判断四边形AECF的形状,并证明你的猜想;
(2)若AB=3,BE=3,求四边形AECF的周长.
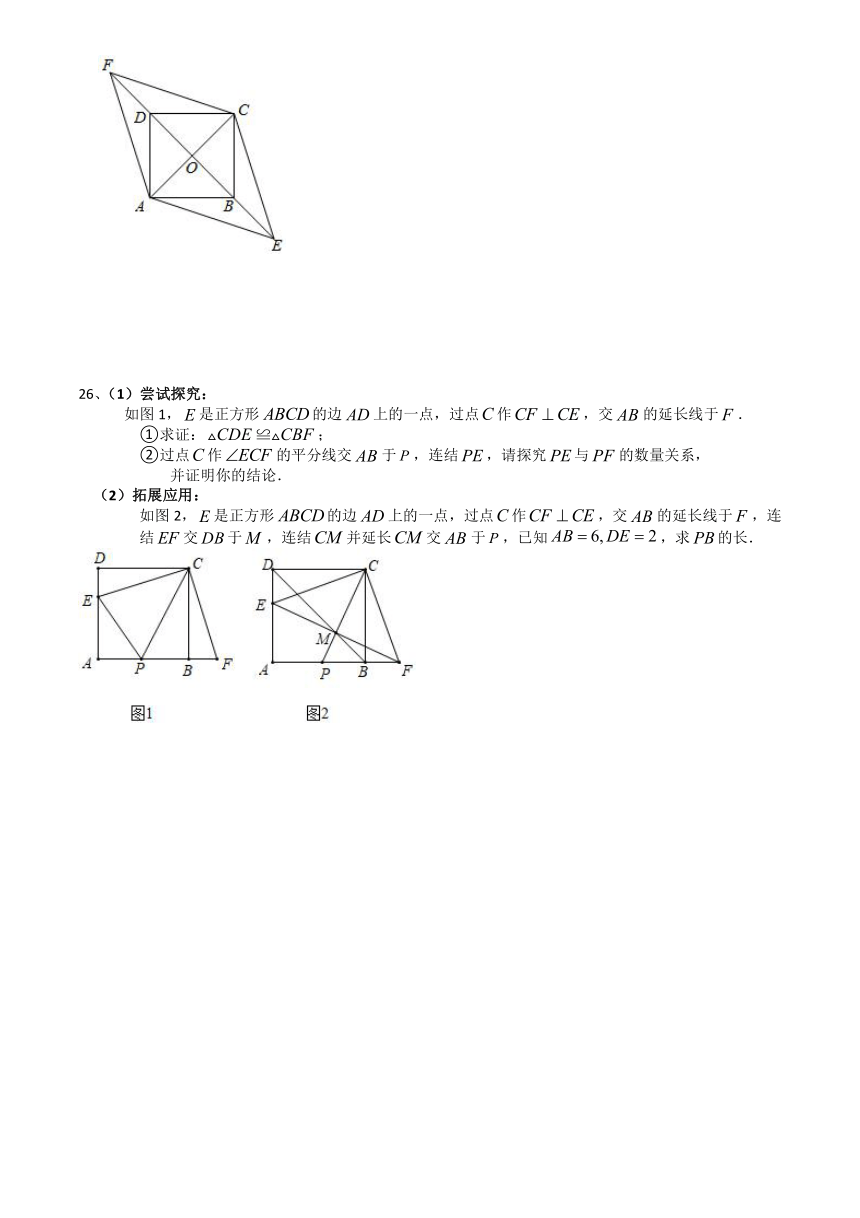
26、(1)尝试探究:
如图1,是正方形的边上的一点,过点作,交的延长线于.
①求证:;
②过点作的平分线交于,连结,请探究与的数量关系,
并证明你的结论.
(2)拓展应用:
如图2,是正方形的边上的一点,过点作,交的延长线于,连结交于,连结并延长交于,已知,求的长.
一、选择题
1、下列说法不正确的是( )
A.一组同旁内角相等的平行四边形是矩形 B.一组邻边相等的菱形是正方形
C.有三个角是直角的四边形是矩形 D.对角线相等的菱形是正方形
解:A、一组同旁内角相等的平行四边形是矩形,正确;
B、一组邻边相等的菱形是正方形,错误;
C、有三个角是直角的四边形是矩形,正确;
D、对角线相等的菱形是正方形,正确.
故选:B.
2、已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.①② B.②③ C.①③ D.②④
解析: 添加①可得平行四边形ABCD是菱形, 添加②可得平行四边形ABCD是矩形,
添加③可得平行四边形ABCD是矩形,添加 ④可得平行四边形ABCD是菱形,
所以选②③不能使得平行四边形ABCD是正方形. 故选B
3、如图,已知P是正方形ABCD的对角线BD上一点,且BP=BC,则∠BCP的度数是( )
A.45° B.22.5° C.67.5° D.75°
解析: ∵四边形ABCD是正方形,
∴∠DBC=45°.
∵BP=BC,∴∠BCP=∠BPC=(180°-45°)=67.5°.故选C
4、如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为( )
A.45° B.55° C.60° D.75°
解:∵四边形ABCD是正方形,∴AB=AD,
又∵△ADE是等边三角形,∴AE=AD=DE,∠DAE=60°,∴AB=AE,
∴∠ABE=∠AEB,∠BAE=90°+60°=150°,
∴∠ABE=(180°﹣150°)÷2=15°,
又∵∠BAC=45°,∴∠BFC=45°+15°=60°.
故选:C.
5、如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.4 B.2 C. D.2
【解析】在正方形ABCD中,OA⊥OB,∠OAD=45°,
∵PE⊥AC,PF⊥BD,∴四边形OEPF为矩形,△AEP是等腰直角三角形,
∴PF=OE,PE=AE,∴PE+PF=AE+OE=OA,
∵正方形ABCD的边长为2,∴OA=AC==.
故选:C.
6、如图,有一个平行四边形ABCD和一个正方形CEFG,其中点E在边AD上.若∠ECD=43°,∠AEF=28°,则∠B的度数为( )
A.55° B.75° C.65° D.60°
【解析】∵四边形CEFG是正方形,∴∠CEF=90°,
∵∠CED=180°﹣∠AEF﹣∠CEF=180°﹣28°﹣90°=62°,
∴∠D=180°﹣∠CED﹣∠ECD=180°﹣62°﹣43°=75°,
∵四边形ABCD为平行四边形,∴∠B=∠D=75°(平行四边形对角相等).
故选:B.
7、如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为( )
A.(1,2.5) B.(1,1+) C.(1,3) D.(﹣1,1+)
解:过D作DH⊥y轴于H,
∵四边形AOCB是矩形,四边形BDEF是正方形,
∴AO=BC,DE=EF=BF,∠AOC=∠DEF=∠BFE=∠BCF=90°,
∴∠OEF+∠EFO=∠BFC+∠EFO=90°,∴∠OEF=∠BFO,
∴△EOF≌△FCB(ASA),∴BC=OF,OE=CF,∴AO=OF,
∵E是OA的中点,∴OE=OA=OF=CF,
∵点C的坐标为(3,0),∴OC=3,
∴OF=OA=2,AE=OE=CF=1,
同理△DHE≌△EOF(ASA),∴DH=OE=1,HE=OF=2,
∴OH=2,∴点D的坐标为(1,3),故选:C.
8、如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E;PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,正确的有( )个.
A.5 B.4 C.3 D.2
【解析】①正确,连接PC,可得PC=EF,PC=PA,∴AP=EF;
②正确;延长AP,交EF于点N,则∠EPN=∠BAP=∠PCE=∠PFE,可得AP⊥EF;
③正确;∠PFE=∠PCE=∠BAP;
④错误,PDPFCE;⑤正确,PB2+PD2=2PA2.
故选:B.
9、如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:
①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的是( )
A.①③ B.①②③④ C.①②③ D.①③④
解:∵四边形ABCD是正方形,E是AD边上的中点,∴AE=DE,AB=CD,∠BAD=∠CDA=90°,
∴△BAE≌△CDE(SAS),∴∠ABE=∠DCE,故①正确;
∵四边形ABCD是正方形,∴AD=DC,∠ADB=∠CDB=45°,DH=DH,
∴△ADH≌△CDH(SAS),∴∠HAD=∠HCD,∵∠ABE=∠DCE, ∴∠ABE=∠HAD,
∵∠BAD=∠BAH+∠DAH=90°,∴∠ABE+∠BAH=90°,∴∠AGB=180°﹣90°=90°,
∴AG⊥BE,故②正确;
∵AD∥BC,∴S△BDE=S△CDE,∴S△BDE﹣S△DEH=S△CDE﹣S△DEH,即;S△BHE=S△CHD,故③正确;
∵△ADH≌△CDH,∴∠AHD=∠CHD,∴∠AHB=∠CHB,
∵∠BHC=∠DHE,∴∠AHB=∠EHD,故④正确;
故选:B.
10、已知:如图,在正方形ABCD外取一点E, 连接AE、BE、DE.过点A作AE的垂线交DE 于点P.
若AE=AP=1,PB=.下列结论:①APD≌△AEB;②点B到直线AE的距离为;③EB⊥ED;④S△APD+S△APB=1+;⑤S正方形ABCD=4+. 其中正确结论的序号是( )
A.①③④ B.①②⑤ C.①③④ D.①③⑤
解:①∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,∴∠EAB=∠PAD,
又∵AE=AP,AB=AD,∴△APD≌△AEB(故①正确);
③∵△APD≌△AEB,∴∠APD=∠AEB,
又∵∠AEB=∠AEP+∠BEP,∠APD=∠AEP+∠PAE,∴∠BEP=∠PAE=90°,∴EB⊥ED(故③正确);
②过B作BF⊥AE,交AE的延长线于F,∵AE=AP,∠EAP=90°,∴∠AEP=∠APE=45°,
又∵③中EB⊥ED,BF⊥AF,∴∠FEB=∠FBE=45°,
又,,(故②不正确);
④如图,连接BD,在Rt△AEP中,∵AE=AP=1,∴EP=,
又,, ∵△APD≌△AEB,∴PD=BE=,
∴S△ABP+S△ADP=S△ABD-S△BDP=S正方形ABCD
⑤∵EF=BF=,∴在Rt△ABF中,,
∴S正方形ABCD=AB2=4+,(故⑤正确)
故选:D.
二、填空题
11、如图,在正方形ABCD中,E是对角线BD上一点,AE的延长线交CD于点F,连接CE.若∠BAE=56°,则∠CEF= °.
【解析】∵正方形ABCD中,∠BAD=∠ADF=90°,∠BAE=56°,∴∠DAF=34°,∠DFE=56°,
∵AD=CD,∠ADE=∠CDE,DE=DE,∴△ADE≌△CDE(SAS),∴∠DCE=∠DAF=34°,
∵∠DFE是△CEF的外角,∴∠CEF=∠DFE﹣∠DCE=56°﹣34°=22°,
故答案为:22.
12、如图,三个边长均为2的正方形重叠在一起,O1,O2是其中两个正方形的中心,
则阴影部分的面积是 2 ?
13、四边形ABCD的对角线AC和BD相交于点O,设有下列条件:①AB=AD;②∠DAB=90°;
③AO=CO,BO=DO;④矩形ABCD;⑤菱形ABCD,⑥正方形ABCD,
则在下列推理不成立的是
A、①④?⑥; B、①③?⑤; C、①②?⑥; D、②③?④
【解答】解:A、由①④得,一组邻边相等的矩形是正方形,故正确;
B、由③得,四边形是平行四边形,再由①,一组邻边相等的平行四边形是菱形,故正确;
C、由①②不能判断四边形是正方形;
D、由③得,四边形是平行四边形,再由②,一个角是直角的平行四边形是矩形,故正确.
故选C.
14、如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,
则正方形ABCD的边长为_____.
解:将△DAF绕点A顺时针旋转90度到△BAF′位置,
由题意可得出:△DAF≌△BAF′,∴DF=BF′,∠DAF=∠BAF′,∴∠EAF′=45°,
在△FAE和△EAF′中 ,∴△FAE≌△EAF′(SAS),∴EF=EF′,
∵△ECF的周长为4,∴EF+EC+FC=FC+CE+EF′=FC+BC+BF′=DF+FC+BC=4,
∴2BC=4,∴BC=2.故答案为:2.
15、如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,
那么CH的长是 .
解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,
∴AB=BC=1,CE=EF=3,∠E=90°,
延长AD交EF于M,连接AC、CF,
则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,∴∠ACD=∠GCF=45°,∴∠ACF=90°,
∵H为AF的中点,∴CH=AF,
在Rt△AMF中,由勾股定理得:AF===2,∴CH=,
故答案为:.
16、如图,在正方形ABCD的各边上顺次截取AE=BF=CG=DH=3,若四边形EFGH面积是10,
则正方形ABCD的面积为 .
【解析】∵AB=BC=CD=AD,AE=BF=CG=DH=3,∴BE=CF=DG=AH,
∵四边形EFGH面积=(AH+3)23×AH3×DG3×CF3×BE=10,
∴AH=BE=CF=DG=1,∴AD=AH+DH=4,
∴正方形ABCD的面积=4×4=16,
故答案为:16.
17、如图,正方形ABCD的边长为2,E为边BC的中点,点P在对角线BD上移动,
则PE+PC的最小值是 .?
18、如图,以的斜边为边,向外作正方形,设正方形的对角线与的交点为O,连接,若,,则的值是__________.
【详解】如图所示:作垂足为F,的延长线,垂足为G,则四边形AFOG为矩形,
四边形BCDE是正方形,OB=OC,,
S
四边形AFDG为正方形
故答案为:.
19、已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
解:∵四边形ABCD为正方形,∴∠BAE=∠D=90°,AB=AD,
∵AB=AD,∠BAE=∠D,AE=DF,∴△ABE≌△DAF(SAS),∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,∴∠DAF+∠BEA=90°,∴∠AGE=∠BGF=90°,
∵点H为BF的中点,∴GH=BF,
∵BC=8,CF=CD﹣DF=8﹣2=6, ∴BF==10,∴GH=5,故答案为:5
20、如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,
下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.
其中正确结论有( )个.
A.2 B.3 C.4 D.5
解答:解:∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,∴AE=EF=AF,∠EAF=60°.∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,,Rt△ABE≌Rt△ADF(HL),∴BE=DF,①正确.∠BAE=∠DAF,
∴∠DAF+∠DAF=30°,即∠DAF=15°②正确,
∵BC=CD,∴BC﹣BE=CD﹣DF,即CE=CF, ∵AE=AF,∴AC垂直平分EF.③正确.
设EC=x,由勾股定理,得EF=x,CG=x,AG=x,∴AC=,
∴AB=,∴BE=﹣x=,∴BE+DF=x﹣x≠x,④错误,
∵S△CEF=,S△ABE==,∴2S△ABE==S△CEF,⑤正确.
综上所述,正确的有4个,故选C.
三、解答题
21、正方形中,对角线、交于点O,E为上一点,延长到点N,使,连接、.
(1)求证:为直角三角形.
(2)若,正方形的边长为6,求的长.
解:(1)证明:∵四边形ABCD是正方形,∴∠ABD=∠CBD=45°,AB=CB,
在△ABE和△CBE中,,∴△ABE≌△CBE(SAS),∴AE=CE;
∵AE=CE,AE=EN,∴∠EAC=∠ECA,CE=EN,∴∠ECN=∠N,
∵∠EAC+∠ECA+∠ECN+∠N=180°,∴∠ACE+∠ECN=90°,即∠ACN=90°,
∴△CAN为直角三角形;
(2)∵正方形的边长为6,∴,
∵,∴,
∵,∴,
∵,∴.
22、如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
【解答】解:(1)证明:∵四边形ABCD为正方形,∴AB⊥BC,∠B=90°.
∵EF⊥AB,EG⊥BC,∴EF∥GB,EG∥BF.
∵∠B=90°,∴四边形BFEG是矩形;
(2)∵正方形ABCD的周长是40cm,∴AB=40÷4=10cm.
∵四边形ABCD为正方形,∴△AEF为等腰直角三角形,∴AF=EF,
∴四边形EFBG的周长C=2(EF+BF)=2(AF+BF)=20cm.
(3)若要四边形BFEG是正方形,只需EF=BF,
∵AF=EF,AB=10cm,∴当AF=5cm时,四边形BFEG是正方形.
23、如图,在△ABC中,AC=BC=6,∠ACB>90°,∠ABC的平分线交AC于点D,E是AB上点,且BE=BC,CF∥ED交BD于点F,连接EF,ED.
(1)求证:四边形CDEF是菱形;
(2)当∠ACB= 度时,四边形CDEF是正方形,请给予证明;并求此时正方形的边长.
【解答】证明:(1)如图,连接EC,交BD于点O
∵BE=BC,BD平分∠ABC∴EO=CO,BD⊥CE∴EF=FC,DE=CD,
∵CF∥DE∴∠DFC=∠FDE,且EO=CO,∠FOC=∠DOE
∴△DOE≌△FOC(AAS)∴DE=CF,∴EF=FC=CD=DE,∴四边形EFCD是菱形
(2)当∠ACB=120度时,四边形CDEF是正方形,
理由如下:∵∠ACB=120°,BC=AC∴∠ABC=∠BAC=30°
∵BD平分∠ABC∴∠DBC=15°,且BD⊥EC,∴∠BCO=75°,∴∠ACE=45°,
∵四边形EFCD是菱形,∴∠FCD=2∠ACE=90°,∴四边形CDEF是正方形,∴∠ADE=90°
如图,过点C作CP⊥AB于点P,
∵BC=AC=6,∠ABC=30°,CP⊥AB
∴CP=3,BPCP=3,AB=2BP=6,∴AE=AB﹣BE=66
∵∠A=30°,∠ADE=90°∴DE=AE=33
24、如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
解:(1)如图,作EM⊥BC于M,EN⊥CD于N,∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,∴EM=EN,
∵∠DEF=90°,∴∠DEN=∠MEF,
∵∠DNE=∠FME=90°,在△DEN和△FEM中,,
∴△DEN≌△FEM(ASA),∴EF=DE,
∵四边形DEFG是矩形,∴矩形DEFG是正方形;
(2)CE+CG的值是定值,定值为6,理由如下:
∵正方形DEFG和正方形ABCD,∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,∴∠CDG=∠ADE,
在∴△ADE和△CDG中,,∴△ADE≌△CDG(SAS),∴AE=CG,
∴CE+CG=CE+AE=AC=AB=×3=6是定值.
25、如图,正方形ABCD的对角线AC、BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)判断四边形AECF的形状,并证明你的猜想;
(2)若AB=3,BE=3,求四边形AECF的周长.
【解析】(1)证明:∵正方形ABCD的对角线AC,BD相交于点O,
∴OA=OC,OB=OD,AC⊥BD.
∵BE=DF,∴OB+BE=OD+DF,即OE=OF.∴四边形AECF是平行四边形.
∵AC⊥EF,∴四边形AECF是菱形.
(2)∵四边形ABCD是正方形,∴AO=AC,BO=BD,AC=BD,AC⊥BD,
∴AO=BO,∠AOB=90°.
在直角△AOB中,由勾股定理知:AB=3,∴AO=BO=3.
∴EO=OB+BE=6.
在△AOE中,∠AOE=90°,AE===3.
∵四边形AECF是菱形,∴AE=EC=CF=AF.
∴四边形AECF的周长=4AE=12.∴四边形AECF的周长是12.
26、(1)尝试探究:
如图1,是正方形的边上的一点,过点作,交的延长线于.
①求证:;
②过点作的平分线交于,连结,请探究与的数量关系,
并证明你的结论.
(2)拓展应用:
如图2,是正方形的边上的一点,过点作,交的延长线于,连结交于,连结并延长交于,已知,求的长.
解:(1)①如图1中,在正方形ABCD中,DC=BC,∠D=∠ABC=∠DCB=90°,
∴∠CBF=180°-∠ABC=90°,
∵CF⊥CE,∴∠ECF=90°,∴∠DCB=∠ECF=90°,∴∠DCE=∠BCF,
∴△CDE≌△CBF(ASA).
②结论:PE=PF.
理由:如图1中,∵△CDE≌△CBF,∴CE=CF,
∵PC=PC,∠PCE=∠PCF,∴△PCE≌△PCF(SAS),∴PE=PF.
(2)如图2中,作EH⊥AD交BD于H,连接PE.
∵四边形ABCD是正方形,∴AB=AD=6,∠A=90°,∠EDH=45°,
∵EH⊥AD,∴∠DEH=∠A=90°,∴EH∥AF,DE=EH=2,
∵△CDE≌△CBF,∴DE=BF=2,∴EH=BF,
∵∠EHM=∠MBF,∠EMH=∠FMB,∴△EMH≌△FMB(AAS),
∵EM=FM,
∵CE=CF,∴PC垂直平分线段EF, ∴PE=PF,设PB=x,则PE=PF=x+2,PA=6-x,
在Rt△APE中,则有(x+2)2=42+(6-x)2,
∴x=3,∴PB=3.
一、选择题
1、下列说法不正确的是( )
A.一组同旁内角相等的平行四边形是矩形 B.一组邻边相等的菱形是正方形
C.有三个角是直角的四边形是矩形 D.对角线相等的菱形是正方形
2、已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.①② B.②③ C.①③ D.②④
3、如图,已知P是正方形ABCD的对角线BD上一点,且BP=BC,则∠BCP的度数是( )
A.45° B.22.5° C.67.5° D.75°
4、如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为( )
A.45° B.55° C.60° D.75°
5、如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.4 B.2 C. D.2
6、如图,有一个平行四边形ABCD和一个正方形CEFG,其中点E在边AD上.若∠ECD=43°,∠AEF=28°,则∠B的度数为( )
A.55° B.75° C.65° D.60°
7、如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为( )
A.(1,2.5) B.(1,1+) C.(1,3) D.(﹣1,1+)
8、如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E;PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,
正确的有( )个.
A.5 B.4 C.3 D.2
9、如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:
①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的是( )
A.①③ B.①②③④ C.①②③ D.①③④
10、已知:如图,在正方形ABCD外取一点E, 连接AE、BE、DE.过点A作AE的垂线交DE 于点P.
若AE=AP=1,PB=.下列结论:①APD≌△AEB;②点B到直线AE的距离为;③EB⊥ED;④S△APD+S△APB=1+;⑤S正方形ABCD=4+. 其中正确结论的序号是( )
A.①③④ B.①②⑤ C.①③④ D.①③⑤
二、填空题
11、如图,在正方形ABCD中,E是对角线BD上一点,AE的延长线交CD于点F,连接CE.若∠BAE=56°,则∠CEF= °.
12、如图,三个边长均为2的正方形重叠在一起,O1,O2是其中两个正方形的中心,
则阴影部分的面积是 ?
13、四边形ABCD的对角线AC和BD相交于点O,设有下列条件:①AB=AD;②∠DAB=90°;
③AO=CO,BO=DO;④矩形ABCD;⑤菱形ABCD,⑥正方形ABCD,
则在下列推理不成立的是
A、①④?⑥; B、①③?⑤; C、①②?⑥; D、②③?④
14、如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,
则正方形ABCD的边长为_____.
15、如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,
那么CH的长是 .
16、如图,在正方形ABCD的各边上顺次截取AE=BF=CG=DH=3,若四边形EFGH面积是10,
则正方形ABCD的面积为 .
17、如图,正方形ABCD的边长为2,E为边BC的中点,点P在对角线BD上移动,
则PE+PC的最小值是 .?
18、如图,以的斜边为边,向外作正方形,设正方形的对角线与的交点为O,连接,若,,则的值是__________.
19、已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
20、如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,
下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.
其中正确结论有( )个.
A.2 B.3 C.4 D.5
三、解答题
21、正方形中,对角线、交于点O,E为上一点,延长到点N,使,连接、.
(1)求证:为直角三角形.
(2)若,正方形的边长为6,求的长.
22、如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
23、如图,在△ABC中,AC=BC=6,∠ACB>90°,∠ABC的平分线交AC于点D,E是AB上点,且BE=BC,CF∥ED交BD于点F,连接EF,ED.
(1)求证:四边形CDEF是菱形;
(2)当∠ACB= 度时,四边形CDEF是正方形,请给予证明;并求此时正方形的边长.
24、如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
25、如图,正方形ABCD的对角线AC、BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)判断四边形AECF的形状,并证明你的猜想;
(2)若AB=3,BE=3,求四边形AECF的周长.
26、(1)尝试探究:
如图1,是正方形的边上的一点,过点作,交的延长线于.
①求证:;
②过点作的平分线交于,连结,请探究与的数量关系,
并证明你的结论.
(2)拓展应用:
如图2,是正方形的边上的一点,过点作,交的延长线于,连结交于,连结并延长交于,已知,求的长.
一、选择题
1、下列说法不正确的是( )
A.一组同旁内角相等的平行四边形是矩形 B.一组邻边相等的菱形是正方形
C.有三个角是直角的四边形是矩形 D.对角线相等的菱形是正方形
解:A、一组同旁内角相等的平行四边形是矩形,正确;
B、一组邻边相等的菱形是正方形,错误;
C、有三个角是直角的四边形是矩形,正确;
D、对角线相等的菱形是正方形,正确.
故选:B.
2、已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.①② B.②③ C.①③ D.②④
解析: 添加①可得平行四边形ABCD是菱形, 添加②可得平行四边形ABCD是矩形,
添加③可得平行四边形ABCD是矩形,添加 ④可得平行四边形ABCD是菱形,
所以选②③不能使得平行四边形ABCD是正方形. 故选B
3、如图,已知P是正方形ABCD的对角线BD上一点,且BP=BC,则∠BCP的度数是( )
A.45° B.22.5° C.67.5° D.75°
解析: ∵四边形ABCD是正方形,
∴∠DBC=45°.
∵BP=BC,∴∠BCP=∠BPC=(180°-45°)=67.5°.故选C
4、如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为( )
A.45° B.55° C.60° D.75°
解:∵四边形ABCD是正方形,∴AB=AD,
又∵△ADE是等边三角形,∴AE=AD=DE,∠DAE=60°,∴AB=AE,
∴∠ABE=∠AEB,∠BAE=90°+60°=150°,
∴∠ABE=(180°﹣150°)÷2=15°,
又∵∠BAC=45°,∴∠BFC=45°+15°=60°.
故选:C.
5、如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.4 B.2 C. D.2
【解析】在正方形ABCD中,OA⊥OB,∠OAD=45°,
∵PE⊥AC,PF⊥BD,∴四边形OEPF为矩形,△AEP是等腰直角三角形,
∴PF=OE,PE=AE,∴PE+PF=AE+OE=OA,
∵正方形ABCD的边长为2,∴OA=AC==.
故选:C.
6、如图,有一个平行四边形ABCD和一个正方形CEFG,其中点E在边AD上.若∠ECD=43°,∠AEF=28°,则∠B的度数为( )
A.55° B.75° C.65° D.60°
【解析】∵四边形CEFG是正方形,∴∠CEF=90°,
∵∠CED=180°﹣∠AEF﹣∠CEF=180°﹣28°﹣90°=62°,
∴∠D=180°﹣∠CED﹣∠ECD=180°﹣62°﹣43°=75°,
∵四边形ABCD为平行四边形,∴∠B=∠D=75°(平行四边形对角相等).
故选:B.
7、如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为( )
A.(1,2.5) B.(1,1+) C.(1,3) D.(﹣1,1+)
解:过D作DH⊥y轴于H,
∵四边形AOCB是矩形,四边形BDEF是正方形,
∴AO=BC,DE=EF=BF,∠AOC=∠DEF=∠BFE=∠BCF=90°,
∴∠OEF+∠EFO=∠BFC+∠EFO=90°,∴∠OEF=∠BFO,
∴△EOF≌△FCB(ASA),∴BC=OF,OE=CF,∴AO=OF,
∵E是OA的中点,∴OE=OA=OF=CF,
∵点C的坐标为(3,0),∴OC=3,
∴OF=OA=2,AE=OE=CF=1,
同理△DHE≌△EOF(ASA),∴DH=OE=1,HE=OF=2,
∴OH=2,∴点D的坐标为(1,3),故选:C.
8、如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E;PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,正确的有( )个.
A.5 B.4 C.3 D.2
【解析】①正确,连接PC,可得PC=EF,PC=PA,∴AP=EF;
②正确;延长AP,交EF于点N,则∠EPN=∠BAP=∠PCE=∠PFE,可得AP⊥EF;
③正确;∠PFE=∠PCE=∠BAP;
④错误,PDPFCE;⑤正确,PB2+PD2=2PA2.
故选:B.
9、如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:
①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的是( )
A.①③ B.①②③④ C.①②③ D.①③④
解:∵四边形ABCD是正方形,E是AD边上的中点,∴AE=DE,AB=CD,∠BAD=∠CDA=90°,
∴△BAE≌△CDE(SAS),∴∠ABE=∠DCE,故①正确;
∵四边形ABCD是正方形,∴AD=DC,∠ADB=∠CDB=45°,DH=DH,
∴△ADH≌△CDH(SAS),∴∠HAD=∠HCD,∵∠ABE=∠DCE, ∴∠ABE=∠HAD,
∵∠BAD=∠BAH+∠DAH=90°,∴∠ABE+∠BAH=90°,∴∠AGB=180°﹣90°=90°,
∴AG⊥BE,故②正确;
∵AD∥BC,∴S△BDE=S△CDE,∴S△BDE﹣S△DEH=S△CDE﹣S△DEH,即;S△BHE=S△CHD,故③正确;
∵△ADH≌△CDH,∴∠AHD=∠CHD,∴∠AHB=∠CHB,
∵∠BHC=∠DHE,∴∠AHB=∠EHD,故④正确;
故选:B.
10、已知:如图,在正方形ABCD外取一点E, 连接AE、BE、DE.过点A作AE的垂线交DE 于点P.
若AE=AP=1,PB=.下列结论:①APD≌△AEB;②点B到直线AE的距离为;③EB⊥ED;④S△APD+S△APB=1+;⑤S正方形ABCD=4+. 其中正确结论的序号是( )
A.①③④ B.①②⑤ C.①③④ D.①③⑤
解:①∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,∴∠EAB=∠PAD,
又∵AE=AP,AB=AD,∴△APD≌△AEB(故①正确);
③∵△APD≌△AEB,∴∠APD=∠AEB,
又∵∠AEB=∠AEP+∠BEP,∠APD=∠AEP+∠PAE,∴∠BEP=∠PAE=90°,∴EB⊥ED(故③正确);
②过B作BF⊥AE,交AE的延长线于F,∵AE=AP,∠EAP=90°,∴∠AEP=∠APE=45°,
又∵③中EB⊥ED,BF⊥AF,∴∠FEB=∠FBE=45°,
又,,(故②不正确);
④如图,连接BD,在Rt△AEP中,∵AE=AP=1,∴EP=,
又,, ∵△APD≌△AEB,∴PD=BE=,
∴S△ABP+S△ADP=S△ABD-S△BDP=S正方形ABCD
⑤∵EF=BF=,∴在Rt△ABF中,,
∴S正方形ABCD=AB2=4+,(故⑤正确)
故选:D.
二、填空题
11、如图,在正方形ABCD中,E是对角线BD上一点,AE的延长线交CD于点F,连接CE.若∠BAE=56°,则∠CEF= °.
【解析】∵正方形ABCD中,∠BAD=∠ADF=90°,∠BAE=56°,∴∠DAF=34°,∠DFE=56°,
∵AD=CD,∠ADE=∠CDE,DE=DE,∴△ADE≌△CDE(SAS),∴∠DCE=∠DAF=34°,
∵∠DFE是△CEF的外角,∴∠CEF=∠DFE﹣∠DCE=56°﹣34°=22°,
故答案为:22.
12、如图,三个边长均为2的正方形重叠在一起,O1,O2是其中两个正方形的中心,
则阴影部分的面积是 2 ?
13、四边形ABCD的对角线AC和BD相交于点O,设有下列条件:①AB=AD;②∠DAB=90°;
③AO=CO,BO=DO;④矩形ABCD;⑤菱形ABCD,⑥正方形ABCD,
则在下列推理不成立的是
A、①④?⑥; B、①③?⑤; C、①②?⑥; D、②③?④
【解答】解:A、由①④得,一组邻边相等的矩形是正方形,故正确;
B、由③得,四边形是平行四边形,再由①,一组邻边相等的平行四边形是菱形,故正确;
C、由①②不能判断四边形是正方形;
D、由③得,四边形是平行四边形,再由②,一个角是直角的平行四边形是矩形,故正确.
故选C.
14、如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,
则正方形ABCD的边长为_____.
解:将△DAF绕点A顺时针旋转90度到△BAF′位置,
由题意可得出:△DAF≌△BAF′,∴DF=BF′,∠DAF=∠BAF′,∴∠EAF′=45°,
在△FAE和△EAF′中 ,∴△FAE≌△EAF′(SAS),∴EF=EF′,
∵△ECF的周长为4,∴EF+EC+FC=FC+CE+EF′=FC+BC+BF′=DF+FC+BC=4,
∴2BC=4,∴BC=2.故答案为:2.
15、如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,
那么CH的长是 .
解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,
∴AB=BC=1,CE=EF=3,∠E=90°,
延长AD交EF于M,连接AC、CF,
则AM=BC+CE=1+3=4,FM=EF﹣AB=3﹣1=2,∠AMF=90°,
∵四边形ABCD和四边形GCEF是正方形,∴∠ACD=∠GCF=45°,∴∠ACF=90°,
∵H为AF的中点,∴CH=AF,
在Rt△AMF中,由勾股定理得:AF===2,∴CH=,
故答案为:.
16、如图,在正方形ABCD的各边上顺次截取AE=BF=CG=DH=3,若四边形EFGH面积是10,
则正方形ABCD的面积为 .
【解析】∵AB=BC=CD=AD,AE=BF=CG=DH=3,∴BE=CF=DG=AH,
∵四边形EFGH面积=(AH+3)23×AH3×DG3×CF3×BE=10,
∴AH=BE=CF=DG=1,∴AD=AH+DH=4,
∴正方形ABCD的面积=4×4=16,
故答案为:16.
17、如图,正方形ABCD的边长为2,E为边BC的中点,点P在对角线BD上移动,
则PE+PC的最小值是 .?
18、如图,以的斜边为边,向外作正方形,设正方形的对角线与的交点为O,连接,若,,则的值是__________.
【详解】如图所示:作垂足为F,的延长线,垂足为G,则四边形AFOG为矩形,
四边形BCDE是正方形,OB=OC,,
S
四边形AFDG为正方形
故答案为:.
19、已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
解:∵四边形ABCD为正方形,∴∠BAE=∠D=90°,AB=AD,
∵AB=AD,∠BAE=∠D,AE=DF,∴△ABE≌△DAF(SAS),∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,∴∠DAF+∠BEA=90°,∴∠AGE=∠BGF=90°,
∵点H为BF的中点,∴GH=BF,
∵BC=8,CF=CD﹣DF=8﹣2=6, ∴BF==10,∴GH=5,故答案为:5
20、如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,
下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.
其中正确结论有( )个.
A.2 B.3 C.4 D.5
解答:解:∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,∴AE=EF=AF,∠EAF=60°.∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,,Rt△ABE≌Rt△ADF(HL),∴BE=DF,①正确.∠BAE=∠DAF,
∴∠DAF+∠DAF=30°,即∠DAF=15°②正确,
∵BC=CD,∴BC﹣BE=CD﹣DF,即CE=CF, ∵AE=AF,∴AC垂直平分EF.③正确.
设EC=x,由勾股定理,得EF=x,CG=x,AG=x,∴AC=,
∴AB=,∴BE=﹣x=,∴BE+DF=x﹣x≠x,④错误,
∵S△CEF=,S△ABE==,∴2S△ABE==S△CEF,⑤正确.
综上所述,正确的有4个,故选C.
三、解答题
21、正方形中,对角线、交于点O,E为上一点,延长到点N,使,连接、.
(1)求证:为直角三角形.
(2)若,正方形的边长为6,求的长.
解:(1)证明:∵四边形ABCD是正方形,∴∠ABD=∠CBD=45°,AB=CB,
在△ABE和△CBE中,,∴△ABE≌△CBE(SAS),∴AE=CE;
∵AE=CE,AE=EN,∴∠EAC=∠ECA,CE=EN,∴∠ECN=∠N,
∵∠EAC+∠ECA+∠ECN+∠N=180°,∴∠ACE+∠ECN=90°,即∠ACN=90°,
∴△CAN为直角三角形;
(2)∵正方形的边长为6,∴,
∵,∴,
∵,∴,
∵,∴.
22、如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
【解答】解:(1)证明:∵四边形ABCD为正方形,∴AB⊥BC,∠B=90°.
∵EF⊥AB,EG⊥BC,∴EF∥GB,EG∥BF.
∵∠B=90°,∴四边形BFEG是矩形;
(2)∵正方形ABCD的周长是40cm,∴AB=40÷4=10cm.
∵四边形ABCD为正方形,∴△AEF为等腰直角三角形,∴AF=EF,
∴四边形EFBG的周长C=2(EF+BF)=2(AF+BF)=20cm.
(3)若要四边形BFEG是正方形,只需EF=BF,
∵AF=EF,AB=10cm,∴当AF=5cm时,四边形BFEG是正方形.
23、如图,在△ABC中,AC=BC=6,∠ACB>90°,∠ABC的平分线交AC于点D,E是AB上点,且BE=BC,CF∥ED交BD于点F,连接EF,ED.
(1)求证:四边形CDEF是菱形;
(2)当∠ACB= 度时,四边形CDEF是正方形,请给予证明;并求此时正方形的边长.
【解答】证明:(1)如图,连接EC,交BD于点O
∵BE=BC,BD平分∠ABC∴EO=CO,BD⊥CE∴EF=FC,DE=CD,
∵CF∥DE∴∠DFC=∠FDE,且EO=CO,∠FOC=∠DOE
∴△DOE≌△FOC(AAS)∴DE=CF,∴EF=FC=CD=DE,∴四边形EFCD是菱形
(2)当∠ACB=120度时,四边形CDEF是正方形,
理由如下:∵∠ACB=120°,BC=AC∴∠ABC=∠BAC=30°
∵BD平分∠ABC∴∠DBC=15°,且BD⊥EC,∴∠BCO=75°,∴∠ACE=45°,
∵四边形EFCD是菱形,∴∠FCD=2∠ACE=90°,∴四边形CDEF是正方形,∴∠ADE=90°
如图,过点C作CP⊥AB于点P,
∵BC=AC=6,∠ABC=30°,CP⊥AB
∴CP=3,BPCP=3,AB=2BP=6,∴AE=AB﹣BE=66
∵∠A=30°,∠ADE=90°∴DE=AE=33
24、如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
解:(1)如图,作EM⊥BC于M,EN⊥CD于N,∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,∴EM=EN,
∵∠DEF=90°,∴∠DEN=∠MEF,
∵∠DNE=∠FME=90°,在△DEN和△FEM中,,
∴△DEN≌△FEM(ASA),∴EF=DE,
∵四边形DEFG是矩形,∴矩形DEFG是正方形;
(2)CE+CG的值是定值,定值为6,理由如下:
∵正方形DEFG和正方形ABCD,∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,∴∠CDG=∠ADE,
在∴△ADE和△CDG中,,∴△ADE≌△CDG(SAS),∴AE=CG,
∴CE+CG=CE+AE=AC=AB=×3=6是定值.
25、如图,正方形ABCD的对角线AC、BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)判断四边形AECF的形状,并证明你的猜想;
(2)若AB=3,BE=3,求四边形AECF的周长.
【解析】(1)证明:∵正方形ABCD的对角线AC,BD相交于点O,
∴OA=OC,OB=OD,AC⊥BD.
∵BE=DF,∴OB+BE=OD+DF,即OE=OF.∴四边形AECF是平行四边形.
∵AC⊥EF,∴四边形AECF是菱形.
(2)∵四边形ABCD是正方形,∴AO=AC,BO=BD,AC=BD,AC⊥BD,
∴AO=BO,∠AOB=90°.
在直角△AOB中,由勾股定理知:AB=3,∴AO=BO=3.
∴EO=OB+BE=6.
在△AOE中,∠AOE=90°,AE===3.
∵四边形AECF是菱形,∴AE=EC=CF=AF.
∴四边形AECF的周长=4AE=12.∴四边形AECF的周长是12.
26、(1)尝试探究:
如图1,是正方形的边上的一点,过点作,交的延长线于.
①求证:;
②过点作的平分线交于,连结,请探究与的数量关系,
并证明你的结论.
(2)拓展应用:
如图2,是正方形的边上的一点,过点作,交的延长线于,连结交于,连结并延长交于,已知,求的长.
解:(1)①如图1中,在正方形ABCD中,DC=BC,∠D=∠ABC=∠DCB=90°,
∴∠CBF=180°-∠ABC=90°,
∵CF⊥CE,∴∠ECF=90°,∴∠DCB=∠ECF=90°,∴∠DCE=∠BCF,
∴△CDE≌△CBF(ASA).
②结论:PE=PF.
理由:如图1中,∵△CDE≌△CBF,∴CE=CF,
∵PC=PC,∠PCE=∠PCF,∴△PCE≌△PCF(SAS),∴PE=PF.
(2)如图2中,作EH⊥AD交BD于H,连接PE.
∵四边形ABCD是正方形,∴AB=AD=6,∠A=90°,∠EDH=45°,
∵EH⊥AD,∴∠DEH=∠A=90°,∴EH∥AF,DE=EH=2,
∵△CDE≌△CBF,∴DE=BF=2,∴EH=BF,
∵∠EHM=∠MBF,∠EMH=∠FMB,∴△EMH≌△FMB(AAS),
∵EM=FM,
∵CE=CF,∴PC垂直平分线段EF, ∴PE=PF,设PB=x,则PE=PF=x+2,PA=6-x,
在Rt△APE中,则有(x+2)2=42+(6-x)2,
∴x=3,∴PB=3.
