2.2乘法公式培优训练(Word版 含答案)
文档属性
| 名称 | 2.2乘法公式培优训练(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 179.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 00:00:00 | ||
图片预览


文档简介
2.2乘法公式培优训练
一、选择题
1.若a+b=10,ab=11,则代数式a2﹣ab+b2的值是( )
A.89 B.﹣89 C.67 D.﹣67
2.下列各式中,能用完全平方公式计算的是( )
A.(a﹣b)(﹣b﹣a) B.(﹣n2﹣m2)(m2+n2)
C. D.(2x﹣3y)(2x+3y)
3.如图是用4个相同的小长方形与1个小正方形密铺而成的大正方形图案,已知其中大正方形的面积为64,小正方形的面积为9.若用x,y分别表示小长方形的长与宽(其中x>y),则下列关系式中错误的是( )
A.4xy+9=64 B.x+y=8 C.x﹣y=3 D.x2﹣y2=9
4.若x2+2(m﹣1)x+16是完全平方式,则m的值为( )
A.±8 B.﹣3或5 C.﹣3 D.5
5.若一个正整数能表示为两个连续奇数的平方差,则称这个正整数为“好数”.下列正整数中能称为“好数”的是( )
A.205 B.250 C.502 D.520
6.计算(1﹣a)(1+a)(1+a2)的结果是( )
A.1﹣a4 B.1+a4 C.1﹣2a2+a4 D.1+2a2+a4
7.已知a﹣b=1,ab=12,则a+b等于( )
A.7 B.5 C.±7 D.±5
8.已知x+y=3,xy=2,则|x﹣y|的值为( )
A.±1 B.1 C.﹣1 D.0
9.若(2x﹣y)2+M=4x2+y2,则整式M为( )
A.﹣4xy B.2xy C.﹣2xy D.4xy
10.已知a+3b=2,则a2﹣9b2+12b的值是( )
A.2 B.3 C.4 D.6
二、填空题
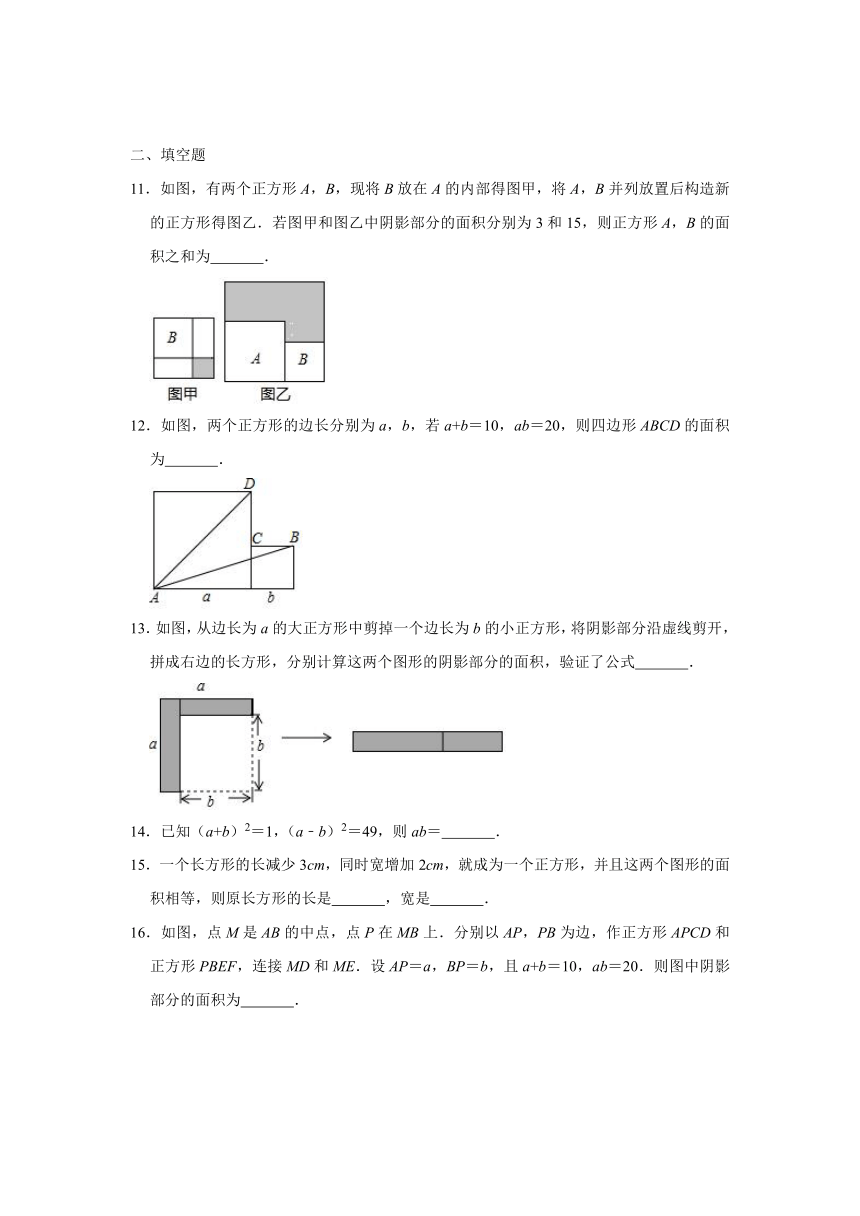
11.如图,有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为3和15,则正方形A,B的面积之和为 .
12.如图,两个正方形的边长分别为a,b,若a+b=10,ab=20,则四边形ABCD的面积为 .
13.如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的长方形,分别计算这两个图形的阴影部分的面积,验证了公式 .
14.已知(a+b)2=1,(a﹣b)2=49,则ab= .
15.一个长方形的长减少3cm,同时宽增加2cm,就成为一个正方形,并且这两个图形的面积相等,则原长方形的长是 ,宽是 .
16.如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连接MD和ME.设AP=a,BP=b,且a+b=10,ab=20.则图中阴影部分的面积为 .
17.若4y2﹣my+25是一个完全平方式,则m= .
18.计算:(a+b﹣c)2= .
19.若n是正整数,且x2n=5,则(2x3n)2÷(4x2n)= .
20.已知4x=10,25y=10,则(x﹣2)(y﹣2)+3(xy﹣3)的值为 .
三、解答题
21.利用乘法公式计算:
(1)198×202;
(2)(2y+1)(﹣2y﹣1).
22.计算:(x﹣y﹣3)(x+y﹣3).
23.已知(x+y)2=9,(x﹣y)2=25,分别求x2+y2和xy的值.
24.若x满足(9﹣x)(x﹣4)=4,求(4﹣x)2+(x﹣9)2的值.
解:设9﹣x=a,x﹣4=b,
则(9﹣x)(x﹣4)=ab=4,a+b=(9﹣x)+(x﹣4)=5,
∴(9﹣x)2+(x﹣4)2=a2+b2=(a+b)2﹣2ab=52﹣2×4=17.
请仿照上面的方法求解下面问题:
(1)若x满足(x﹣2004)2+(x﹣2007)2=31,求(x﹣2004)(x﹣2007)的值;
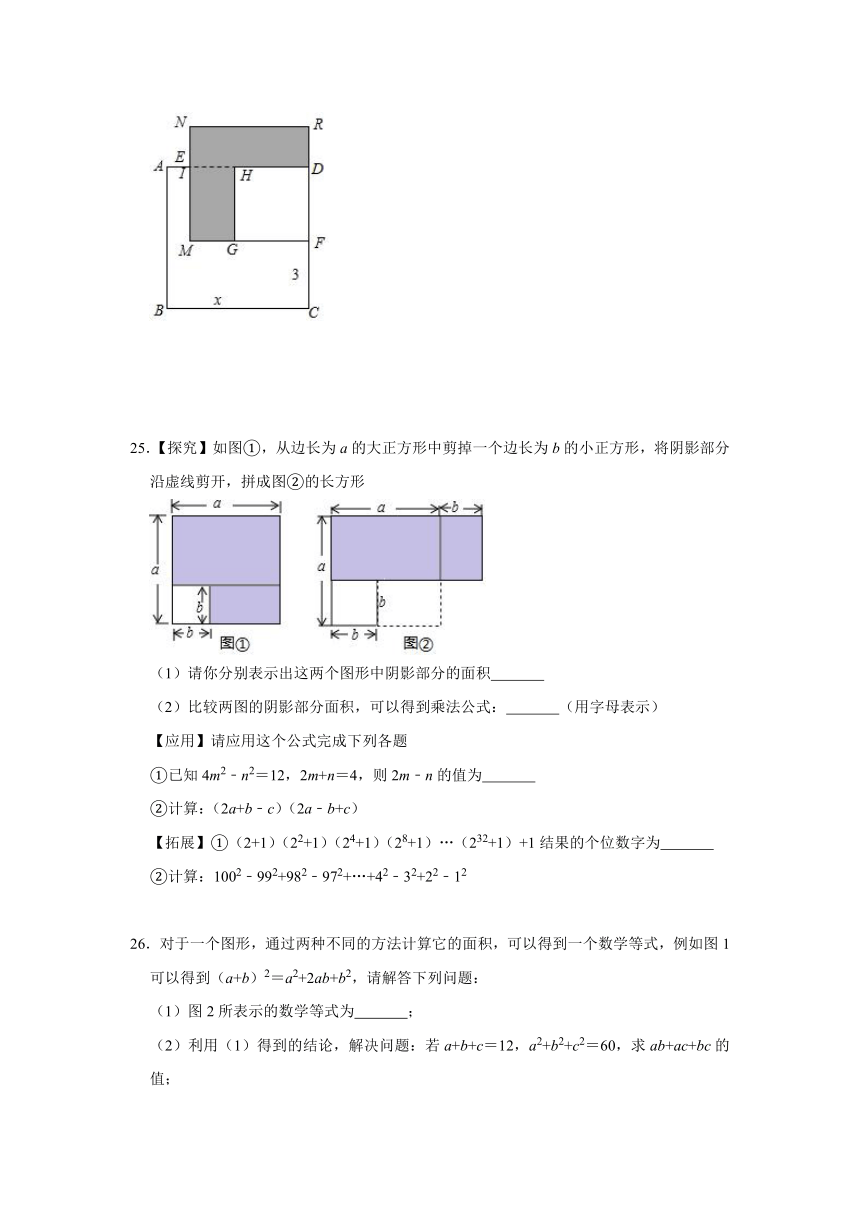
(2)已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是48,分别以MF、DF作正方形MFRN和正方形GFDH,求阴影部分的面积.
25.【探究】如图①,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成图②的长方形
(1)请你分别表示出这两个图形中阴影部分的面积
(2)比较两图的阴影部分面积,可以得到乘法公式: (用字母表示)
【应用】请应用这个公式完成下列各题
①已知4m2﹣n2=12,2m+n=4,则2m﹣n的值为
②计算:(2a+b﹣c)(2a﹣b+c)
【拓展】①(2+1)(22+1)(24+1)(28+1)…(232+1)+1结果的个位数字为
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12
26.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题:
(1)图2所表示的数学等式为 ;
(2)利用(1)得到的结论,解决问题:若a+b+c=12,a2+b2+c2=60,求ab+ac+bc的值;
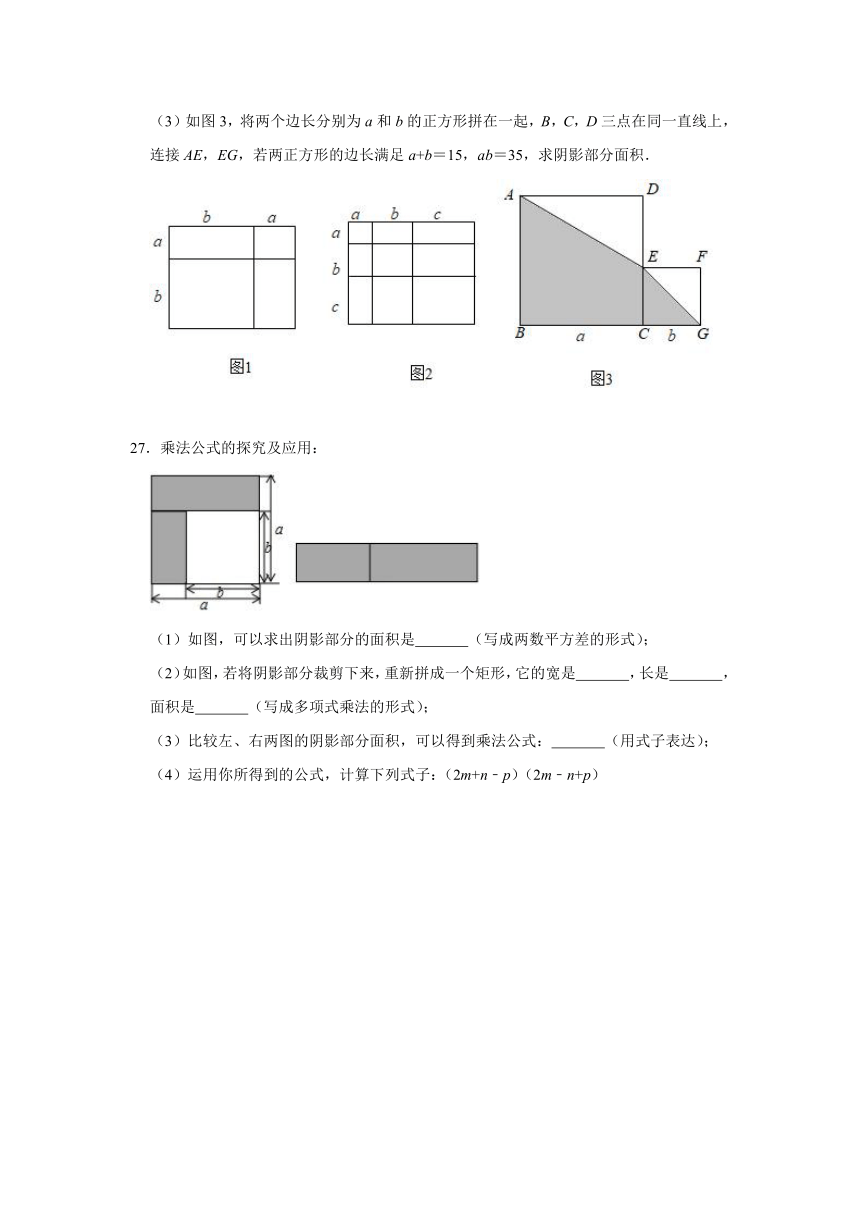
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,D三点在同一直线上,连接AE,EG,若两正方形的边长满足a+b=15,ab=35,求阴影部分面积.
27.乘法公式的探究及应用:
(1)如图,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较左、右两图的阴影部分面积,可以得到乘法公式: (用式子表达);
(4)运用你所得到的公式,计算下列式子:(2m+n﹣p)(2m﹣n+p)
参考答案
1.解:把a+b=10两边平方得:
(a+b)2=a2+b2+2ab=100,
把ab=11代入得:
a2+b2=78,
∴原式=78﹣11=67,
故选:C.
2.解:A、原式=b2﹣a2,本选项不合题意;
B、原式=﹣(m2+n2)2,本选项符合题意;
C、原式=q2﹣p2,本选项不合题意;
D、原式=4x2﹣9y2,本选项不合题意,
故选:B.
3.解:A、因为正方形图案面积从整体看是64,从组合来看,可以是(x+y)2,还可以是(4xy+4),即4xy+4=64,故此选项正确;
B、因为正方形图案的边长8,同时还可用(x+y)来表示,故此选项正确;
C、中间小正方形的边长为3,同时根据长方形长宽也可表示为x﹣y,故此选项正确;
D、根据A、B可知x+y=8,x﹣y=3,则x2﹣y2=(x+y)(x﹣y)=24,故此选项错误;
故选:D.
4.解:∵x2+2(m﹣1)x+16是完全平方式,而16=42,
∴m﹣1=4或m﹣1=﹣4,
∴m=5或﹣3.
故选:B.
5.解:根据平方差公式得:
(2n+1)2﹣(2n﹣1)2=(2n+1+2n﹣1)(2n+1﹣2n+1)=4n×2=8n.
所以两个连续奇数构造的“好数”是8的倍数
205,250,502都不能被8整除,只有520能够被8整除.
故选:D.
6.解:(1﹣a)(1+a)(1+a2)=(1﹣a2)(1+a2)=1﹣a4.
故选:A.
7.解:∵a﹣b=1,ab=12,
∴(a+b)2=a2+2ab+b2=(a﹣b)2+4ab=1+48=49,
∴a+b=±7,
故选:C.
8.解:∵x+y=3,xy=2,
∴(x﹣y)2=(x+y)2﹣4xy=32﹣4×2=1.
∴x﹣y=±1,
∴|x﹣y|=1.
故选:B.
9.解:因为(2x﹣y)2+M=4x2+y2,(2x﹣y)2+4xy=4x2+y2,
所以M=4xy,
故选:D.
10.解:因为a+3b=2,
所以a2﹣9b2+12b=(a+3b)(a﹣3b)+12b=2(a﹣3b)+12b
=2a﹣6b+12b=2a+6b=2(a+3b)=2×2=4,故选:C.
11.解:如图所示:
设正方形A、B的边长分别为x,y,依题意得:
,
化简得:
由①+②得:
x2+y2=18,
∴,
故答案为18.
12.解:根据题意可得,四边形ABCD的面积
=(a2+b2)﹣﹣b(a+b)
=(a2+b2﹣ab)
=(a2+b2+2ab﹣3ab)
=[(a+b)2﹣3ab];
代入a+b=10,ab=20,可得:
四边形ABCD的面积=(10×10﹣20×3)÷2=20.
故答案为:20.
13.解:第一个图形阴影部分的面积是a2﹣b2,
第二个图形的面积是(a+b)(a﹣b).
则a2﹣b2=(a+b)(a﹣b).
故答案为:a2﹣b2=(a+b)(a﹣b).
14.解:∵(a+b)2=1,(a﹣b)2=49,
∴a2+2ab+b2=1,a2﹣2ab+b2=49,
两式相减,可得4ab=﹣48,
∴ab=﹣12.
故答案为:﹣12.
15.解:设这个长方形的长为xcm,宽为ycm,
由题意得,,
解得:.
故答案为:9cm,4cm.
16.解:∵AP=a,BP=b,点M是AB的中点,
∴AM=BM=,
∴S阴影=S正方形APCD+S正方形BEFP﹣S△ADM﹣S△BEM
=a2+b2﹣a×﹣b×
=a2+b2﹣(a+b)2=(a+b)2﹣2ab﹣(a+b)2=100﹣40﹣25=35,
故答案为:35.
17.解:∵4y2﹣my+25是一个完全平方式,
∴(2y)2±2?2y?5+52,
即﹣my=±2?2y?5,
∴m=±20,
故答案为:±20.
18.解:原式=[(a+b)﹣c]2
=(a+b)2﹣2(a+b)c+c2
=a2+2ab+b2﹣2ac﹣2bc+c2,
故答案为:a2+2ab+b2﹣2ac﹣2bc+c2.
19.解:∵n是正整数,且x2n=5,
∴(2x3n)2÷(4x2n)=4x6n÷(4x2n)=(4÷4)x6n﹣2n=x4n=(x2n)2=52=25.
故答案为:25.
20.解:∵
∴由①得4xy=10y,③
由②得25xy=10x,④
∴③×④得4xy?25xy=10y?10x,即(4×25)xy=10x+y,
∴(102)xy=10x+y,
∴102xy=10x+y,
∴2xy=x+y
(x﹣2)(y﹣2)+3(xy﹣3)=xy﹣2x﹣2y+4+3xy﹣9
=4xy﹣2(x+y)﹣5=4xy﹣2×2xy﹣5=﹣5
故答案为:﹣5.
21.解:(1)原式=(200﹣2)(200+2)=2002﹣22=40000﹣4=39996;
(2)原式=﹣(2y+1)2=﹣(4y2+2×2y×1+12)=﹣(4y2+4y+1)=﹣4y2﹣4y﹣1.
22.解:(x﹣y﹣3)(x+y﹣3)=(x﹣3)2﹣y2=x2﹣6x+9﹣y2.
23.解:∵(x+y)2=9,(x﹣y)2=25,
∴两式相加,得(x+y)2+(x﹣y)2=2x2+2y2=34,
则x2+y2=17;
两式相减,得(x+y)2﹣(x﹣y)2=4xy=﹣16,
则xy=﹣4.
24.解:(1)设x﹣2004=a,x﹣2007=b,
∴a2+b2=31,a﹣b=3,
∴﹣2(x﹣2004)(x﹣2007)=﹣2ab=(a﹣b)2﹣(a2+b2)=9﹣31=﹣22,
∴(x﹣2004)(x﹣2007)=11;
(2)∵正方形ABCD的边长为x,AE=1,CF=3,
∴FM=DE=x﹣1,DF=x﹣3,
∴(x﹣1)?(x﹣3)=48,
∴(x﹣1)﹣(x﹣3)=2,
∴阴影部分的面积=FM2﹣DF2=(x﹣1)2﹣(x﹣3)2.
设(x﹣1)=a,(x﹣3)=b,则(x﹣1)(x﹣3)=ab=48,a﹣b=(x﹣1)﹣(x﹣3)=2,
∴(a+b)2=(a﹣b)2+4ab=4+192=196,
∵a>0,b>0,
∴a+b>0,
∴a+b=14,
∴(x﹣1)2﹣(x﹣3)2=a2﹣b2=(a+b)(a﹣b)=14×2=28.
即阴影部分的面积是28.
25.解:(1)图①按照正方形面积公式可得:a2﹣b2;
图②按照长方形面积公式可得:(a+b)(a﹣b).
故答案为:a2﹣b2;(a+b)(a﹣b).
(2)令(1)中两式相等可得:(a+b)(a﹣b)=a2﹣b2
故答案为:(a+b)(a﹣b)=a2﹣b2.
【应用】①∵4m2﹣n2=12,2m+n=4,4m2﹣n2=(2m+n)(2m﹣n)
∴(2m﹣n)=12÷4=3
故答案为:3.
②(2a+b﹣c)(2a﹣b+c)=[2a+(b﹣c)][2a﹣(b﹣c)]
=4a2﹣(b﹣c)2=4a2﹣b2+2bc﹣c2
【拓展】①
原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)…(232+1)+1
=(22﹣1)(22+1)(24+1)(28+1)…(232+1)+1
=(24﹣1)(24+1)(28+1)…(232+1)+1
=(28﹣1)(28+1)…(232+1)+1=(216﹣1)…(232+1)+1=264﹣1+1=264
∵2的正整数次方的尾数为2,4,8,6循环,64÷4=16
故答案为:6.
②原式=(100+99)(100﹣99)+(98+97)(98﹣97)+…+(4+3)(4﹣3)+(2+1)(2﹣1)=100+99+98+97+…+4+3+2+1=5050
26.解:(1)由图可得,(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
故答案为:(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)由(1)可得:==42;
(3)=
====95.
27.解:(1)由图可得,阴影部分的面积=a2﹣b2;
故答案为:a2﹣b2;
(2)由图可得,矩形的宽是a﹣b,长是a+b,面积是(a+b)(a﹣b);
故答案为:a﹣b,a+b,(a+b)(a﹣b);
(3)依据两图的阴影部分面积相等,可以得到乘法公式(a+b)(a﹣b)=a2﹣b2;
故答案为:(a+b)(a﹣b)=a2﹣b2;
(4)(2m+n﹣p)(2m﹣n+p)=(2m)2﹣(n﹣p)2=4m2﹣(n2﹣2np+p2)
=4m2﹣n2+2np﹣p2.
一、选择题
1.若a+b=10,ab=11,则代数式a2﹣ab+b2的值是( )
A.89 B.﹣89 C.67 D.﹣67
2.下列各式中,能用完全平方公式计算的是( )
A.(a﹣b)(﹣b﹣a) B.(﹣n2﹣m2)(m2+n2)
C. D.(2x﹣3y)(2x+3y)
3.如图是用4个相同的小长方形与1个小正方形密铺而成的大正方形图案,已知其中大正方形的面积为64,小正方形的面积为9.若用x,y分别表示小长方形的长与宽(其中x>y),则下列关系式中错误的是( )
A.4xy+9=64 B.x+y=8 C.x﹣y=3 D.x2﹣y2=9
4.若x2+2(m﹣1)x+16是完全平方式,则m的值为( )
A.±8 B.﹣3或5 C.﹣3 D.5
5.若一个正整数能表示为两个连续奇数的平方差,则称这个正整数为“好数”.下列正整数中能称为“好数”的是( )
A.205 B.250 C.502 D.520
6.计算(1﹣a)(1+a)(1+a2)的结果是( )
A.1﹣a4 B.1+a4 C.1﹣2a2+a4 D.1+2a2+a4
7.已知a﹣b=1,ab=12,则a+b等于( )
A.7 B.5 C.±7 D.±5
8.已知x+y=3,xy=2,则|x﹣y|的值为( )
A.±1 B.1 C.﹣1 D.0
9.若(2x﹣y)2+M=4x2+y2,则整式M为( )
A.﹣4xy B.2xy C.﹣2xy D.4xy
10.已知a+3b=2,则a2﹣9b2+12b的值是( )
A.2 B.3 C.4 D.6
二、填空题
11.如图,有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为3和15,则正方形A,B的面积之和为 .
12.如图,两个正方形的边长分别为a,b,若a+b=10,ab=20,则四边形ABCD的面积为 .
13.如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的长方形,分别计算这两个图形的阴影部分的面积,验证了公式 .
14.已知(a+b)2=1,(a﹣b)2=49,则ab= .
15.一个长方形的长减少3cm,同时宽增加2cm,就成为一个正方形,并且这两个图形的面积相等,则原长方形的长是 ,宽是 .
16.如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连接MD和ME.设AP=a,BP=b,且a+b=10,ab=20.则图中阴影部分的面积为 .
17.若4y2﹣my+25是一个完全平方式,则m= .
18.计算:(a+b﹣c)2= .
19.若n是正整数,且x2n=5,则(2x3n)2÷(4x2n)= .
20.已知4x=10,25y=10,则(x﹣2)(y﹣2)+3(xy﹣3)的值为 .
三、解答题
21.利用乘法公式计算:
(1)198×202;
(2)(2y+1)(﹣2y﹣1).
22.计算:(x﹣y﹣3)(x+y﹣3).
23.已知(x+y)2=9,(x﹣y)2=25,分别求x2+y2和xy的值.
24.若x满足(9﹣x)(x﹣4)=4,求(4﹣x)2+(x﹣9)2的值.
解:设9﹣x=a,x﹣4=b,
则(9﹣x)(x﹣4)=ab=4,a+b=(9﹣x)+(x﹣4)=5,
∴(9﹣x)2+(x﹣4)2=a2+b2=(a+b)2﹣2ab=52﹣2×4=17.
请仿照上面的方法求解下面问题:
(1)若x满足(x﹣2004)2+(x﹣2007)2=31,求(x﹣2004)(x﹣2007)的值;
(2)已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是48,分别以MF、DF作正方形MFRN和正方形GFDH,求阴影部分的面积.
25.【探究】如图①,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成图②的长方形
(1)请你分别表示出这两个图形中阴影部分的面积
(2)比较两图的阴影部分面积,可以得到乘法公式: (用字母表示)
【应用】请应用这个公式完成下列各题
①已知4m2﹣n2=12,2m+n=4,则2m﹣n的值为
②计算:(2a+b﹣c)(2a﹣b+c)
【拓展】①(2+1)(22+1)(24+1)(28+1)…(232+1)+1结果的个位数字为
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12
26.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题:
(1)图2所表示的数学等式为 ;
(2)利用(1)得到的结论,解决问题:若a+b+c=12,a2+b2+c2=60,求ab+ac+bc的值;
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,D三点在同一直线上,连接AE,EG,若两正方形的边长满足a+b=15,ab=35,求阴影部分面积.
27.乘法公式的探究及应用:
(1)如图,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较左、右两图的阴影部分面积,可以得到乘法公式: (用式子表达);
(4)运用你所得到的公式,计算下列式子:(2m+n﹣p)(2m﹣n+p)
参考答案
1.解:把a+b=10两边平方得:
(a+b)2=a2+b2+2ab=100,
把ab=11代入得:
a2+b2=78,
∴原式=78﹣11=67,
故选:C.
2.解:A、原式=b2﹣a2,本选项不合题意;
B、原式=﹣(m2+n2)2,本选项符合题意;
C、原式=q2﹣p2,本选项不合题意;
D、原式=4x2﹣9y2,本选项不合题意,
故选:B.
3.解:A、因为正方形图案面积从整体看是64,从组合来看,可以是(x+y)2,还可以是(4xy+4),即4xy+4=64,故此选项正确;
B、因为正方形图案的边长8,同时还可用(x+y)来表示,故此选项正确;
C、中间小正方形的边长为3,同时根据长方形长宽也可表示为x﹣y,故此选项正确;
D、根据A、B可知x+y=8,x﹣y=3,则x2﹣y2=(x+y)(x﹣y)=24,故此选项错误;
故选:D.
4.解:∵x2+2(m﹣1)x+16是完全平方式,而16=42,
∴m﹣1=4或m﹣1=﹣4,
∴m=5或﹣3.
故选:B.
5.解:根据平方差公式得:
(2n+1)2﹣(2n﹣1)2=(2n+1+2n﹣1)(2n+1﹣2n+1)=4n×2=8n.
所以两个连续奇数构造的“好数”是8的倍数
205,250,502都不能被8整除,只有520能够被8整除.
故选:D.
6.解:(1﹣a)(1+a)(1+a2)=(1﹣a2)(1+a2)=1﹣a4.
故选:A.
7.解:∵a﹣b=1,ab=12,
∴(a+b)2=a2+2ab+b2=(a﹣b)2+4ab=1+48=49,
∴a+b=±7,
故选:C.
8.解:∵x+y=3,xy=2,
∴(x﹣y)2=(x+y)2﹣4xy=32﹣4×2=1.
∴x﹣y=±1,
∴|x﹣y|=1.
故选:B.
9.解:因为(2x﹣y)2+M=4x2+y2,(2x﹣y)2+4xy=4x2+y2,
所以M=4xy,
故选:D.
10.解:因为a+3b=2,
所以a2﹣9b2+12b=(a+3b)(a﹣3b)+12b=2(a﹣3b)+12b
=2a﹣6b+12b=2a+6b=2(a+3b)=2×2=4,故选:C.
11.解:如图所示:
设正方形A、B的边长分别为x,y,依题意得:
,
化简得:
由①+②得:
x2+y2=18,
∴,
故答案为18.
12.解:根据题意可得,四边形ABCD的面积
=(a2+b2)﹣﹣b(a+b)
=(a2+b2﹣ab)
=(a2+b2+2ab﹣3ab)
=[(a+b)2﹣3ab];
代入a+b=10,ab=20,可得:
四边形ABCD的面积=(10×10﹣20×3)÷2=20.
故答案为:20.
13.解:第一个图形阴影部分的面积是a2﹣b2,
第二个图形的面积是(a+b)(a﹣b).
则a2﹣b2=(a+b)(a﹣b).
故答案为:a2﹣b2=(a+b)(a﹣b).
14.解:∵(a+b)2=1,(a﹣b)2=49,
∴a2+2ab+b2=1,a2﹣2ab+b2=49,
两式相减,可得4ab=﹣48,
∴ab=﹣12.
故答案为:﹣12.
15.解:设这个长方形的长为xcm,宽为ycm,
由题意得,,
解得:.
故答案为:9cm,4cm.
16.解:∵AP=a,BP=b,点M是AB的中点,
∴AM=BM=,
∴S阴影=S正方形APCD+S正方形BEFP﹣S△ADM﹣S△BEM
=a2+b2﹣a×﹣b×
=a2+b2﹣(a+b)2=(a+b)2﹣2ab﹣(a+b)2=100﹣40﹣25=35,
故答案为:35.
17.解:∵4y2﹣my+25是一个完全平方式,
∴(2y)2±2?2y?5+52,
即﹣my=±2?2y?5,
∴m=±20,
故答案为:±20.
18.解:原式=[(a+b)﹣c]2
=(a+b)2﹣2(a+b)c+c2
=a2+2ab+b2﹣2ac﹣2bc+c2,
故答案为:a2+2ab+b2﹣2ac﹣2bc+c2.
19.解:∵n是正整数,且x2n=5,
∴(2x3n)2÷(4x2n)=4x6n÷(4x2n)=(4÷4)x6n﹣2n=x4n=(x2n)2=52=25.
故答案为:25.
20.解:∵
∴由①得4xy=10y,③
由②得25xy=10x,④
∴③×④得4xy?25xy=10y?10x,即(4×25)xy=10x+y,
∴(102)xy=10x+y,
∴102xy=10x+y,
∴2xy=x+y
(x﹣2)(y﹣2)+3(xy﹣3)=xy﹣2x﹣2y+4+3xy﹣9
=4xy﹣2(x+y)﹣5=4xy﹣2×2xy﹣5=﹣5
故答案为:﹣5.
21.解:(1)原式=(200﹣2)(200+2)=2002﹣22=40000﹣4=39996;
(2)原式=﹣(2y+1)2=﹣(4y2+2×2y×1+12)=﹣(4y2+4y+1)=﹣4y2﹣4y﹣1.
22.解:(x﹣y﹣3)(x+y﹣3)=(x﹣3)2﹣y2=x2﹣6x+9﹣y2.
23.解:∵(x+y)2=9,(x﹣y)2=25,
∴两式相加,得(x+y)2+(x﹣y)2=2x2+2y2=34,
则x2+y2=17;
两式相减,得(x+y)2﹣(x﹣y)2=4xy=﹣16,
则xy=﹣4.
24.解:(1)设x﹣2004=a,x﹣2007=b,
∴a2+b2=31,a﹣b=3,
∴﹣2(x﹣2004)(x﹣2007)=﹣2ab=(a﹣b)2﹣(a2+b2)=9﹣31=﹣22,
∴(x﹣2004)(x﹣2007)=11;
(2)∵正方形ABCD的边长为x,AE=1,CF=3,
∴FM=DE=x﹣1,DF=x﹣3,
∴(x﹣1)?(x﹣3)=48,
∴(x﹣1)﹣(x﹣3)=2,
∴阴影部分的面积=FM2﹣DF2=(x﹣1)2﹣(x﹣3)2.
设(x﹣1)=a,(x﹣3)=b,则(x﹣1)(x﹣3)=ab=48,a﹣b=(x﹣1)﹣(x﹣3)=2,
∴(a+b)2=(a﹣b)2+4ab=4+192=196,
∵a>0,b>0,
∴a+b>0,
∴a+b=14,
∴(x﹣1)2﹣(x﹣3)2=a2﹣b2=(a+b)(a﹣b)=14×2=28.
即阴影部分的面积是28.
25.解:(1)图①按照正方形面积公式可得:a2﹣b2;
图②按照长方形面积公式可得:(a+b)(a﹣b).
故答案为:a2﹣b2;(a+b)(a﹣b).
(2)令(1)中两式相等可得:(a+b)(a﹣b)=a2﹣b2
故答案为:(a+b)(a﹣b)=a2﹣b2.
【应用】①∵4m2﹣n2=12,2m+n=4,4m2﹣n2=(2m+n)(2m﹣n)
∴(2m﹣n)=12÷4=3
故答案为:3.
②(2a+b﹣c)(2a﹣b+c)=[2a+(b﹣c)][2a﹣(b﹣c)]
=4a2﹣(b﹣c)2=4a2﹣b2+2bc﹣c2
【拓展】①
原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)…(232+1)+1
=(22﹣1)(22+1)(24+1)(28+1)…(232+1)+1
=(24﹣1)(24+1)(28+1)…(232+1)+1
=(28﹣1)(28+1)…(232+1)+1=(216﹣1)…(232+1)+1=264﹣1+1=264
∵2的正整数次方的尾数为2,4,8,6循环,64÷4=16
故答案为:6.
②原式=(100+99)(100﹣99)+(98+97)(98﹣97)+…+(4+3)(4﹣3)+(2+1)(2﹣1)=100+99+98+97+…+4+3+2+1=5050
26.解:(1)由图可得,(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
故答案为:(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)由(1)可得:==42;
(3)=
====95.
27.解:(1)由图可得,阴影部分的面积=a2﹣b2;
故答案为:a2﹣b2;
(2)由图可得,矩形的宽是a﹣b,长是a+b,面积是(a+b)(a﹣b);
故答案为:a﹣b,a+b,(a+b)(a﹣b);
(3)依据两图的阴影部分面积相等,可以得到乘法公式(a+b)(a﹣b)=a2﹣b2;
故答案为:(a+b)(a﹣b)=a2﹣b2;
(4)(2m+n﹣p)(2m﹣n+p)=(2m)2﹣(n﹣p)2=4m2﹣(n2﹣2np+p2)
=4m2﹣n2+2np﹣p2.
