2020-2021学年人教版八年级下册数学第18章18.2特殊的平行四边形同步习题练(word解析版)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学第18章18.2特殊的平行四边形同步习题练(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 00:00:00 | ||
图片预览

文档简介
2020-2021学年人教版八年级下册数学第18章18.2特殊的平行四边形同步习题练
一、单选题
1.下列说法不正确的是( )
A.两组对边分别相等的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.一个角是直角的平行四边形是正方形
D.对角线互相平分且垂直的四边形是菱形
2.矩形具有而一般平行四边形不具有的性质是( ).
A.对角线相等 B.对角相等 C.对边相等 D.对角线互相平分
3.如图,菱形中,分别是的中点,若,则菱形的周长为( )
A.24 B.18 C.12 D.9
4.如图,己知四边形ABCD是平行四边形,下列说法正确的是( )
A.若,则平行四边形ABCD是矩形
B.若,则平行四边形ABCD是正方形
C.若,则平行四边形ABCD是矩形
D.若,则平行四边形ABCD是正方形
5.如图,以为斜边的和位于直线的同侧,连接.若,则的长为( )
A.3 B.4 C. D.
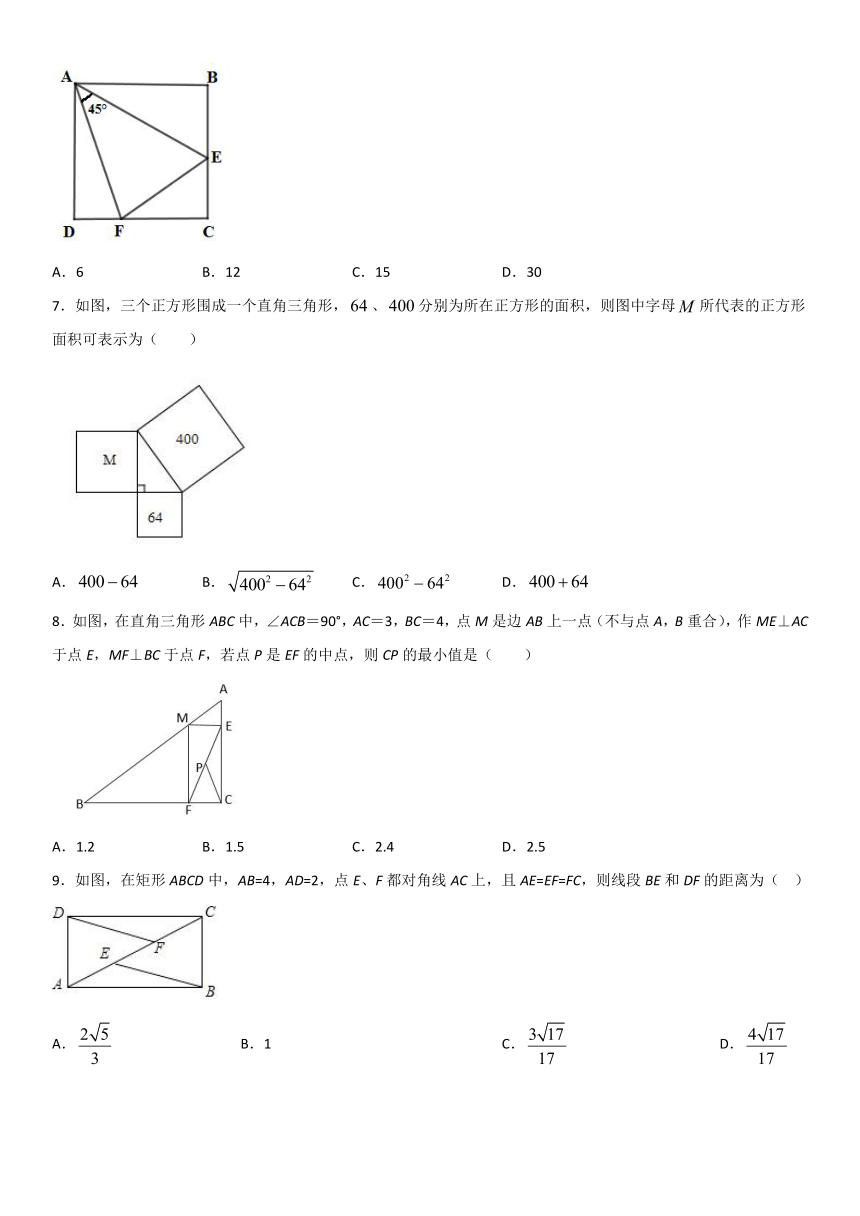
6.如图,点、分别在正方形的边、上,,已知(正方形的四条边都相等,四个内角都是直角),.则的面积( )
A.6 B.12 C.15 D.30
7.如图,三个正方形围成一个直角三角形,、分别为所在正方形的面积,则图中字母所代表的正方形面积可表示为( )
A. B. C. D.
8.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2 B.1.5 C.2.4 D.2.5
9.如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为(?? )
A.????????????????????????????????????B.1???????????????????????????????????? C.???????????????????????????????????? D.
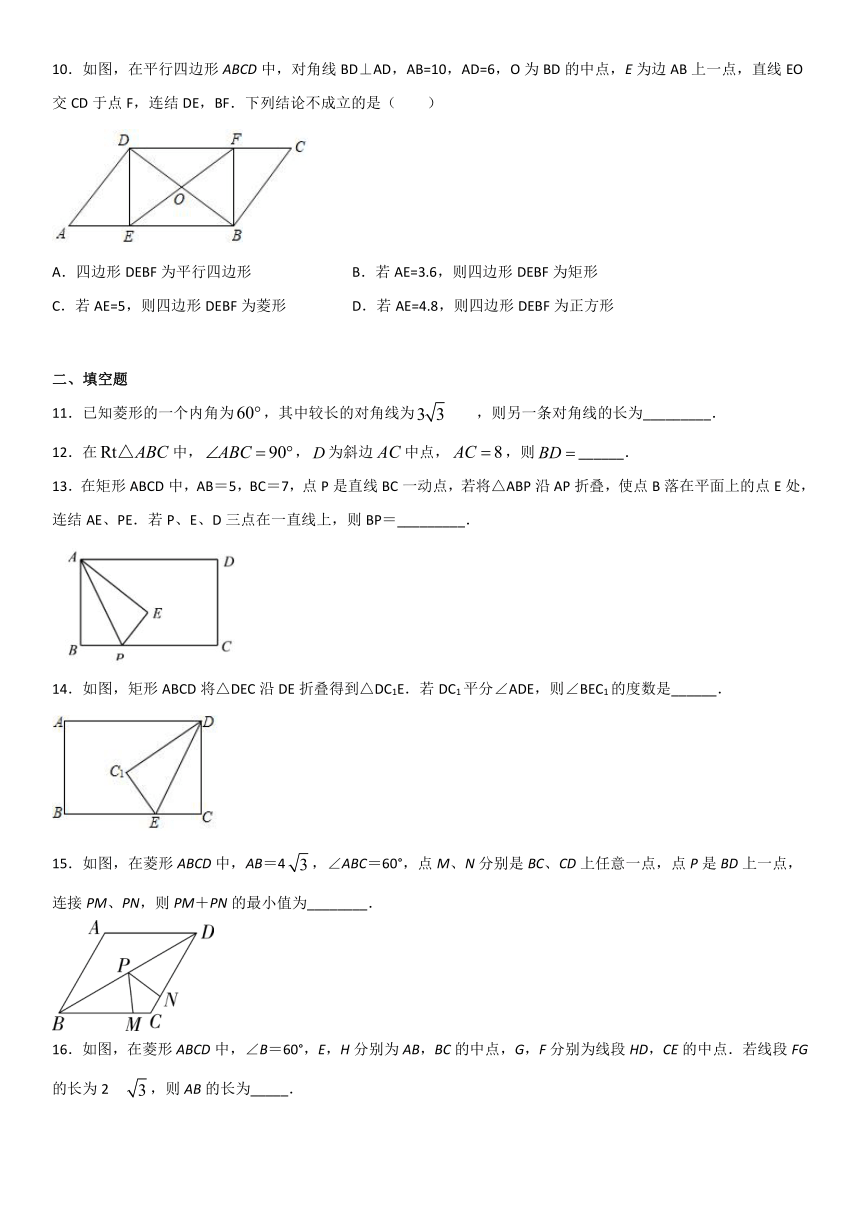
10.如图,在平行四边形ABCD中,对角线BD⊥AD,AB=10,AD=6,O为BD的中点,E为边AB上一点,直线EO交CD于点F,连结DE,BF.下列结论不成立的是( )
A.四边形DEBF为平行四边形 B.若AE=3.6,则四边形DEBF为矩形
C.若AE=5,则四边形DEBF为菱形 D.若AE=4.8,则四边形DEBF为正方形
二、填空题
11.已知菱形的一个内角为,其中较长的对角线为,则另一条对角线的长为_________.
12.在中,,为斜边中点,,则______.
13.在矩形ABCD中,AB=5,BC=7,点P是直线BC一动点,若将△ABP沿AP折叠,使点B落在平面上的点E处,连结AE、PE.若P、E、D三点在一直线上,则BP=_________.
14.如图,矩形ABCD将△DEC沿DE折叠得到△DC1E.若DC1平分∠ADE,则∠BEC1的度数是______.
15.如图,在菱形ABCD中,AB=4,∠ABC=60°,点M、N分别是BC、CD上任意一点,点P是BD上一点,连接PM、PN,则PM+PN的最小值为________.
16.如图,在菱形ABCD中,∠B=60°,E,H分别为AB,BC的中点,G,F分别为线段HD,CE的中点.若线段FG的长为2?,则AB的长为_____.
三、解答题
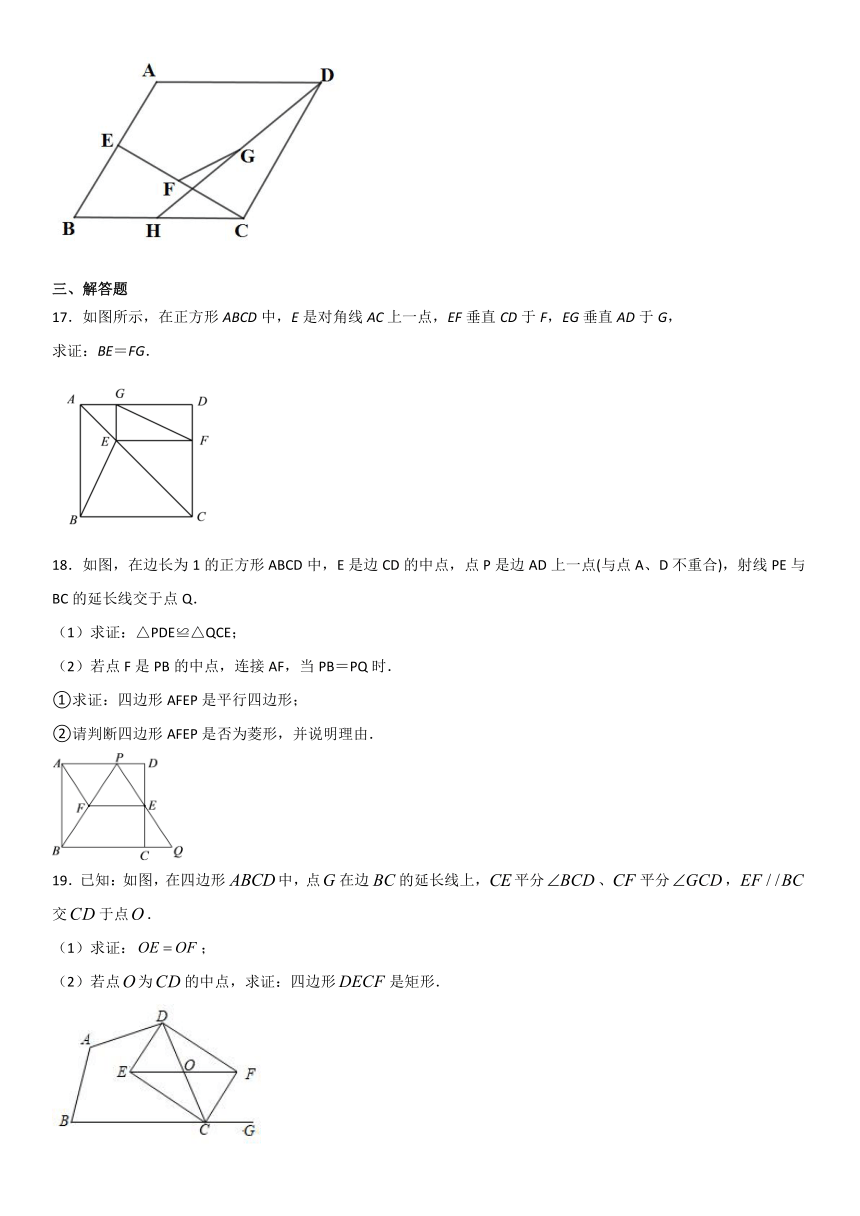
17.如图所示,在正方形ABCD中,E是对角线AC上一点,EF垂直CD于F,EG垂直AD于G,
求证:BE=FG.
18.如图,在边长为1的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.
(1)求证:△PDE≌△QCE;
(2)若点F是PB的中点,连接AF,当PB=PQ时.
①求证:四边形AFEP是平行四边形;
②请判断四边形AFEP是否为菱形,并说明理由.
19.已知:如图,在四边形中,点在边的延长线上,平分、平分,交于点.
(1)求证:;
(2)若点为的中点,求证:四边形是矩形.
20.如图,四边形ABCD中,∠B=60°,AC=BC,点E在AB上,将CE绕点C顺时针旋转60°得CF,且点F在AD上.
(1)求证:AF=BE;
(2)若AE=DF,求证:四边形ABCD是菱形;
(3)若BC=2,求四边形AFCE的面积.
21.如图,已知正方形的边长为3,菱形的三个顶点E、G、H分别在正方形的边、、上,,连接.
(1)当时,求证:菱形为正方形;
(2)设,请用x的代数式表示的面积;
(3)当时,求的度数.
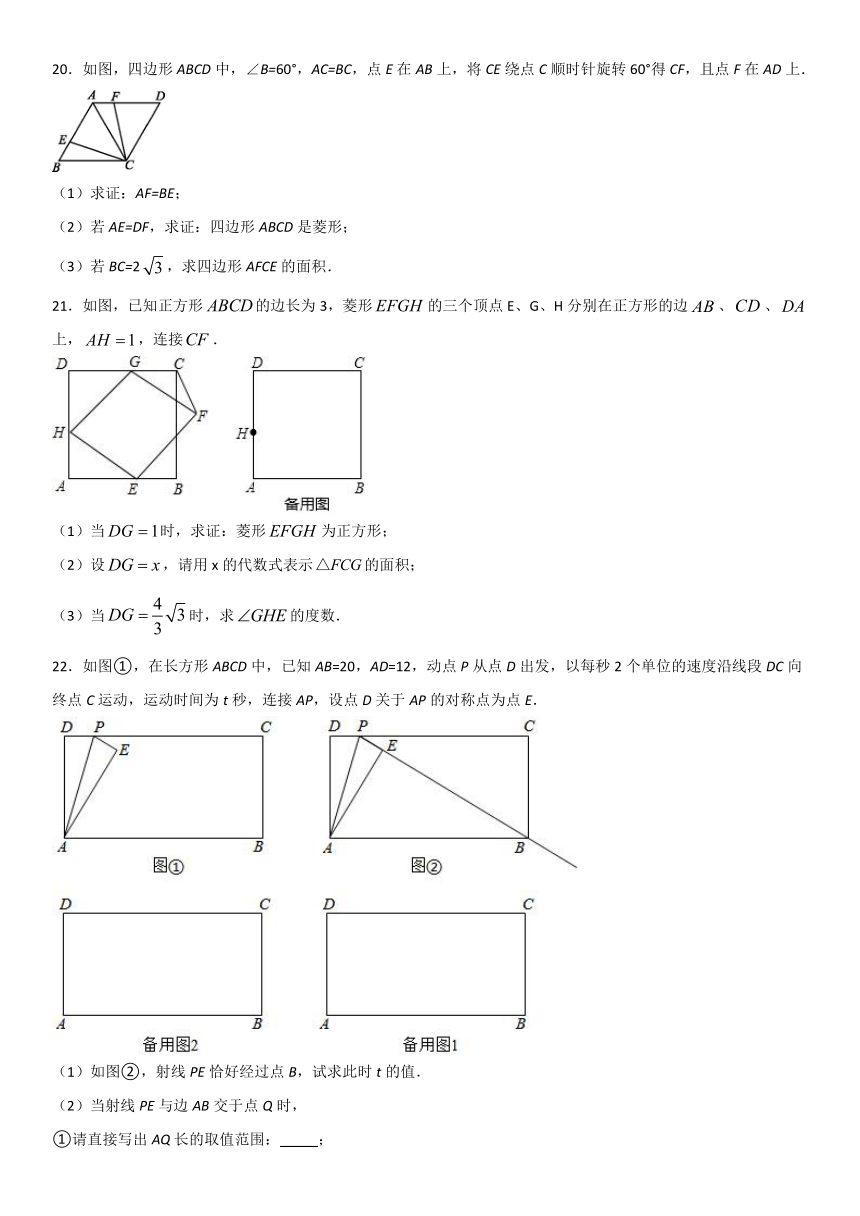
22.如图①,在长方形ABCD中,已知AB=20,AD=12,动点P从点D出发,以每秒2个单位的速度沿线段DC向终点C运动,运动时间为t秒,连接AP,设点D关于AP的对称点为点E.
(1)如图②,射线PE恰好经过点B,试求此时t的值.
(2)当射线PE与边AB交于点Q时,
①请直接写出AQ长的取值范围: ;
②是否存在这样的t的值,使得QE=QB?若存在,请求出所有符合题意的t的值;若不存在,请说明理由.
参考答案
1.C
【详解】
解:A、两组对边分别平行的四边形是平行四边形,正确;
B、对角线相等的平行四边形是矩形,正确;
C、一个角是直角的平行四边形是矩形,故原说法错误;
D、对角线互相平分且垂直的四边形是菱形,正确;
故选:C.
2.A
【详解】
解:∵矩形的对边平行且相等,对角线互相平分且相等;
平行四边形的对边平行且相等,对角线互相平分;
∴矩形具有而平行四边形不具有的性质是对角线相等;
故选:A.
3.A
【详解】
解:∵分别是的中点,,
∴,
∵四边形是菱形,
∴菱形的周长为,
故选:A.
4.C
【详解】
解:A、若AB=AD,则?ABCD是菱形,选项说法错误;
B、若AB=AD,则?ABCD是菱形,选项说法错误;
C、若AB⊥BC,则?ABCD是矩形,选项说法正确;
D、若AC⊥BD,则?ABCD是菱形,选项说法错误;
故选:C.
5.C
【详解】
取AB的中点O,连结OD,OC,
∵和的斜边为AB,
∴,,
∴,
∴,,,
在四边形ABCD中,,
∵,
∴,
∵,
∴,
∴是等腰直角三角形,
∵,
∴,
∴,
故选:C.
6.C
【详解】
解:延长CD到G,使DG=BE,连接AG,
在正方形ABCD中,AB=AD,
,
,
,
,
,
,
,
又,
(SAS),
,
设BE=DG=x,则EC=6-x,FC=4,EF=FG=x+2,
在中,,
,
解得,x=3,
,
,
故选:C.
7.A
【详解】
设的边长为,直角三角形斜边的长为,另一直角边为,
则,,
如图所示,在该直角三角形中,由勾股定理得:
,
故选:A.
8.A
【详解】
解:连接CM,如图所示:
∵∠ACB=90°,AC=3,BC=4,
∴AB=,
∵ME⊥AC,MF⊥BC,∠ACB=90°,
∴四边形CEMF是矩形,
∴EF=CM,
∵点P是EF的中点,
∴CP=EF,
当CM⊥AB时,CM最短,
此时EF也最小,则CP最小,
∵△ABC的面积=AB×CM=AC×BC,
∴CM==,
∴CP=EF=CM=1.2,
故选:A.
9.D
【详解】
解:∵矩形ABCD中,AB=4,AD=2,
∴AB∥CD,AB=CD,∠BAD=∠ABC=90°,矩形ABCD的面积=4×2=8,
∴∠DCF=∠BAE,
在△DCF和△BAE中, ,
∴△DCF≌△BAE(SAS),
∴DF=BE,∠DFC=∠BEA,
∴∠DFE=∠BEF,
延长BE交AD于G,延长DF交BC于H,作FM⊥BE于M,CN⊥BE于N,则FM∥CN,
∴DF∥BE,
∵AE=EF=FC,
∴△BCE的面积= ×8= ,
∵AE=EF=FC,
∴AG=DG=1,BH=CH=1,
∴BG= = ,
∴BE= BG= ,
∵ BE?CN= ,
∴CN= ,
∵FM∥CN,EF=FC,
∴FM= CN= ,
故选择:D.
10.D
【详解】
A.∵四边形ABCD是平行四边形
∴
∴
∵O为BD的中点
∴
在与中
∴
∴
∵
∴四边形DEBF为平行四边形,故A选项正确;
B.假设
∵,,
∴
∴
∴
∵
∴
则当时,
∵四边形DEBF为平行四边形
∴四边形DEBF为矩形,故B选项正确;
C.∵,
∴E是AB中点
∵
∴
∵四边形DEBF为平行四边形
∴四边形DEBF为菱形,故C选项正确;
D.当时与时矛盾,则DE不垂直于AB,则四边形DEBF不为矩形,则也不可能为正方形,故D选项错误,
故选:D.
11.3
【详解】
如图所示菱形ABCD,由题意得,
∵,
∴,
在中,
,
OA=,
由勾股定理得即,
解得,
∴.
12.4
【详解】
∵∠ABC=90°,D为斜边AC的中线,
∵AC=8,
∴ ,
故答案为:4.
13.7+2或7﹣2
【详解】
解:由折叠的性质可得:,,,,
∵四边形ABCD是矩形,
∴BC=AD=7,AB=CD=5,AD∥BC,
当点P在线段BC上时,且P、E、D三点在一条直线上时,如图所示:
∴,
∴,
∴,
设,则,
∴在中,,
解得:(不符合题意,舍去);
当点P在线段BC外时,且P、E、D三点在一条直线上时,如图所示:
∴,
∴,
∴,
设,则,
∵,
∴在中,,
解得:(不符合题意,舍去);
∴,
综上所述:当P、E、D三点在一条直线上时,或;
故答案为或.
14.60°
【详解】
解:在矩形ABCD中,∠ADC=90°,
由折叠可知:△DCE≌△DC?E,
∴∠DEC=∠DEC?,∠CDE=∠C?DE,
∵DC?平分∠ADE,
∴∠ADC?=∠C?DE,
∴∠CDE=∠C?DE=∠ADC?,
∵∠CDE+∠C?DE+∠ADC?=∠ADC=90°,
∴∠CDE=∠C?DE=∠ADC?=30°,
∴∠DEC=∠DEC?=90°-30°=60°,
∴ ∠BEC?=180°-∠DEC-∠DEC?=60°,
故答案为:.
15.6
【详解】
如图,作点N关于BD对称的点N′,过点N′作N′M⊥BC于点M,
∴MN′与BD的交点P即满足PM+PN的值最小,
∴MN′=AB·sin∠ABC=4×=6.
故答案为:6.
16.8
【详解】
解:连接CG并延长,交AD于点M,连接EM,作AN⊥EM于N,
∵四边形ABCD为菱形,∠B=60°,
∴AD∥BC,AD=BC=AB
∴∠EAM=120°,∠DMG=∠HCG,
∵G为DH中点,
∴DG=HG,
∵∠MGD=∠CGH,
∴△DMG≌△HCG,
∴DM=HC,CG=MG,
∵H为BC中点,
∴,
∴AM=,
∵E为AB中点,
∴AE=,
∴AE=AM,
∵F为CE中点,G为CM中点,
∴FG为△CEM中位线,
∴,
∵AE=AM,∠EAM=120°,AN⊥EM,
∴EN=EM=,∠AEN=30°,
∴AE=2AN=4,
∴AB=2AE=8.
故答案为:8
17.
【详解】
证明:如图,连接DE,
在正方形ABCD中,AB=AD,∠BAC=∠DAC,
∵在△ABE和△ADE中,
∴△ABE≌△ADE(SAS),
∴BE=DE,
∵EF⊥CD于F,EG⊥AD于G,∠ADC=90°,
∴四边形EFDG是矩形,
∴DE=FG,
∴BE=FG.
18.【详解】
(1)证明:∵四边形ABCD是正方形,
∴∠D=∠BCD=90°,
∴∠ECQ=90°=∠D.
∵E是CD的中点,
∴DE=CE.
又∵∠DEP=∠CEQ,
∴△PDE≌△QCE ;
(2)①证明:①∵PB=PQ,
∴∠PBQ=∠Q,
∵AD∥BC,
∴∠APB=∠PBQ=∠Q=∠EPD,
∵△PDE≌△QCE,
∴PE=QE,
∵PF=BF,
∴是的中位线,
∴EF∥BQ,
∴在Rt△PAB中,AF=PF=BF,
∴∠APF=∠PAF,
∴∠PAF=∠EPD,
∴PE∥AF,
∵EF∥BQ∥AD,
∴四边形AFEP是平行四边形;
②四边形AFEP不是菱形;
理由:
设PD=x,则AP=1-x.由(1)可知△PDE≌△QCE,
∴CQ=PD=x,
∴BQ=BC+CQ=1+x,
∵点E,F分别是PQ,PB的中点,
∴EF是△PBQ的中位线,
∴EF=BQ=,
由①可知AP=EF,即1-x=,
解得:x=,
∴PD=,AP=
在Rt△PDE中,DE=,
则PE==,
∴AP≠PE,
∴四边形AFEP不是菱形.
19.
【详解】
证明:(1)∵平分、平分
∴,
∵∥,
∴,
∴,
∴,,
∴.
(2)∵点为的中点,
∴,又,
∴四边形是平行四边形
∵平分、平分,
∴,
∴
∵,
∴
∵四边形是平行四边形,
∴平行四边形是矩形.
20.
【详解】
(1)证明:∵AC=BC,∠B=60°,
∴△ABC是等边三角形,
∴AB=BC=AC,∠ACB=60°.
∵∠ECF=60°,∴∠ACB=∠ECF,
∴∠ECB=∠ACF.
在△BCE和△ACF中,
∴△BCE≌△ACF(SAS),
∴AF=BE.
(2)证明:由(1)得∠FAC=∠EBC=∠ACB=60°,
∴AF∥BC.
∵AF=BE,AE=DF,
∴AD=AB.
∴AD=BC,
∴四边形ABCD是平行四边形.
∵AB=BC,
∴?ABCD是菱形.
(3)∵△BCE≌△ACF,
∴四边形AFCE的面积=△AFC的面积+△ACE的面积
=△BEC的面积+△ACE的面积
=△ABC的面积,
∵△ABC是一个等边三角形且BC=2,
∴四边形AFCE的面积=×2×2×=3.
21.
【详解】
解:(1)在正方形中,
,
.
又,
在和中,
,,,
,
.
,.
所以菱形是正方形;
(2)如图1,过点作交所在直线于,联结.
,
.
,
.
,
在和中,
,.
.
.
即无论菱形如何变化,点到直线的距离始终为定值1,
;
(3)如图2,当时,
在中,,根据勾股定理得,;
,
在中,根据勾股定理得,,
过点作于,
在中,根据勾股定理得,,
,
为等边三角形.
.
22.(1)t=2;(2)①12≤AQ≤20;②存在这样的t值,使得QE=QB,t的值为3.6或10.
【详解】
(1)如图1,
∵AB∥CD,
∴∠DPA=∠PAB,
由轴对称得:∠DPA=∠EPA,
∴∠EPA=∠PAB,
∴BP=AB=20,
在Rt△PCB中,由勾股定理得:PC==16,
∴PD=4=2t,
∴t=2;
(2)①由(1)可知:当t=2时,Q与B重合,此时AQ=AB=20,
如图2,当PQ⊥AB时,E与Q重合,此时AQ=AD=12,
∴12≤AQ≤20,
故答案为:12≤AQ≤20;
②存在,分两种情况:
当点E在矩形ABCD内部时,如图3,
∵QE=PQ﹣PE=PQ﹣DP=PQ﹣2t,
∵QE=QB,PQ=AQ,
∴QB=AQ﹣2t,
∵AQ+BQ=AB=20,
∴AQ+AQ﹣2t=20,
∴AQ=10+t,
在Rt△EQA中,AQ=10+t,QE=AQ﹣2t=10-t,AE=12,
∴,
解得:t=3.6;
当点E在矩形ABCD的外部时,如图4,
∵QE=PE﹣PQ=DP﹣PQ=2t﹣PQ,
∵QE=QB,PQ=AQ,
∴BQ=2t﹣AQ,
∴AB﹣AQ=2t﹣AQ,
∴AB=2t,
∴t==10(此时P与C重合),
综上,存在这样的t值,使得QE=QB,t的值为3.6或10.
一、单选题
1.下列说法不正确的是( )
A.两组对边分别相等的四边形是平行四边形
B.对角线相等的平行四边形是矩形
C.一个角是直角的平行四边形是正方形
D.对角线互相平分且垂直的四边形是菱形
2.矩形具有而一般平行四边形不具有的性质是( ).
A.对角线相等 B.对角相等 C.对边相等 D.对角线互相平分
3.如图,菱形中,分别是的中点,若,则菱形的周长为( )
A.24 B.18 C.12 D.9
4.如图,己知四边形ABCD是平行四边形,下列说法正确的是( )
A.若,则平行四边形ABCD是矩形
B.若,则平行四边形ABCD是正方形
C.若,则平行四边形ABCD是矩形
D.若,则平行四边形ABCD是正方形
5.如图,以为斜边的和位于直线的同侧,连接.若,则的长为( )
A.3 B.4 C. D.
6.如图,点、分别在正方形的边、上,,已知(正方形的四条边都相等,四个内角都是直角),.则的面积( )
A.6 B.12 C.15 D.30
7.如图,三个正方形围成一个直角三角形,、分别为所在正方形的面积,则图中字母所代表的正方形面积可表示为( )
A. B. C. D.
8.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2 B.1.5 C.2.4 D.2.5
9.如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为(?? )
A.????????????????????????????????????B.1???????????????????????????????????? C.???????????????????????????????????? D.
10.如图,在平行四边形ABCD中,对角线BD⊥AD,AB=10,AD=6,O为BD的中点,E为边AB上一点,直线EO交CD于点F,连结DE,BF.下列结论不成立的是( )
A.四边形DEBF为平行四边形 B.若AE=3.6,则四边形DEBF为矩形
C.若AE=5,则四边形DEBF为菱形 D.若AE=4.8,则四边形DEBF为正方形
二、填空题
11.已知菱形的一个内角为,其中较长的对角线为,则另一条对角线的长为_________.
12.在中,,为斜边中点,,则______.
13.在矩形ABCD中,AB=5,BC=7,点P是直线BC一动点,若将△ABP沿AP折叠,使点B落在平面上的点E处,连结AE、PE.若P、E、D三点在一直线上,则BP=_________.
14.如图,矩形ABCD将△DEC沿DE折叠得到△DC1E.若DC1平分∠ADE,则∠BEC1的度数是______.
15.如图,在菱形ABCD中,AB=4,∠ABC=60°,点M、N分别是BC、CD上任意一点,点P是BD上一点,连接PM、PN,则PM+PN的最小值为________.
16.如图,在菱形ABCD中,∠B=60°,E,H分别为AB,BC的中点,G,F分别为线段HD,CE的中点.若线段FG的长为2?,则AB的长为_____.
三、解答题
17.如图所示,在正方形ABCD中,E是对角线AC上一点,EF垂直CD于F,EG垂直AD于G,
求证:BE=FG.
18.如图,在边长为1的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.
(1)求证:△PDE≌△QCE;
(2)若点F是PB的中点,连接AF,当PB=PQ时.
①求证:四边形AFEP是平行四边形;
②请判断四边形AFEP是否为菱形,并说明理由.
19.已知:如图,在四边形中,点在边的延长线上,平分、平分,交于点.
(1)求证:;
(2)若点为的中点,求证:四边形是矩形.
20.如图,四边形ABCD中,∠B=60°,AC=BC,点E在AB上,将CE绕点C顺时针旋转60°得CF,且点F在AD上.
(1)求证:AF=BE;
(2)若AE=DF,求证:四边形ABCD是菱形;
(3)若BC=2,求四边形AFCE的面积.
21.如图,已知正方形的边长为3,菱形的三个顶点E、G、H分别在正方形的边、、上,,连接.
(1)当时,求证:菱形为正方形;
(2)设,请用x的代数式表示的面积;
(3)当时,求的度数.
22.如图①,在长方形ABCD中,已知AB=20,AD=12,动点P从点D出发,以每秒2个单位的速度沿线段DC向终点C运动,运动时间为t秒,连接AP,设点D关于AP的对称点为点E.
(1)如图②,射线PE恰好经过点B,试求此时t的值.
(2)当射线PE与边AB交于点Q时,
①请直接写出AQ长的取值范围: ;
②是否存在这样的t的值,使得QE=QB?若存在,请求出所有符合题意的t的值;若不存在,请说明理由.
参考答案
1.C
【详解】
解:A、两组对边分别平行的四边形是平行四边形,正确;
B、对角线相等的平行四边形是矩形,正确;
C、一个角是直角的平行四边形是矩形,故原说法错误;
D、对角线互相平分且垂直的四边形是菱形,正确;
故选:C.
2.A
【详解】
解:∵矩形的对边平行且相等,对角线互相平分且相等;
平行四边形的对边平行且相等,对角线互相平分;
∴矩形具有而平行四边形不具有的性质是对角线相等;
故选:A.
3.A
【详解】
解:∵分别是的中点,,
∴,
∵四边形是菱形,
∴菱形的周长为,
故选:A.
4.C
【详解】
解:A、若AB=AD,则?ABCD是菱形,选项说法错误;
B、若AB=AD,则?ABCD是菱形,选项说法错误;
C、若AB⊥BC,则?ABCD是矩形,选项说法正确;
D、若AC⊥BD,则?ABCD是菱形,选项说法错误;
故选:C.
5.C
【详解】
取AB的中点O,连结OD,OC,
∵和的斜边为AB,
∴,,
∴,
∴,,,
在四边形ABCD中,,
∵,
∴,
∵,
∴,
∴是等腰直角三角形,
∵,
∴,
∴,
故选:C.
6.C
【详解】
解:延长CD到G,使DG=BE,连接AG,
在正方形ABCD中,AB=AD,
,
,
,
,
,
,
,
又,
(SAS),
,
设BE=DG=x,则EC=6-x,FC=4,EF=FG=x+2,
在中,,
,
解得,x=3,
,
,
故选:C.
7.A
【详解】
设的边长为,直角三角形斜边的长为,另一直角边为,
则,,
如图所示,在该直角三角形中,由勾股定理得:
,
故选:A.
8.A
【详解】
解:连接CM,如图所示:
∵∠ACB=90°,AC=3,BC=4,
∴AB=,
∵ME⊥AC,MF⊥BC,∠ACB=90°,
∴四边形CEMF是矩形,
∴EF=CM,
∵点P是EF的中点,
∴CP=EF,
当CM⊥AB时,CM最短,
此时EF也最小,则CP最小,
∵△ABC的面积=AB×CM=AC×BC,
∴CM==,
∴CP=EF=CM=1.2,
故选:A.
9.D
【详解】
解:∵矩形ABCD中,AB=4,AD=2,
∴AB∥CD,AB=CD,∠BAD=∠ABC=90°,矩形ABCD的面积=4×2=8,
∴∠DCF=∠BAE,
在△DCF和△BAE中, ,
∴△DCF≌△BAE(SAS),
∴DF=BE,∠DFC=∠BEA,
∴∠DFE=∠BEF,
延长BE交AD于G,延长DF交BC于H,作FM⊥BE于M,CN⊥BE于N,则FM∥CN,
∴DF∥BE,
∵AE=EF=FC,
∴△BCE的面积= ×8= ,
∵AE=EF=FC,
∴AG=DG=1,BH=CH=1,
∴BG= = ,
∴BE= BG= ,
∵ BE?CN= ,
∴CN= ,
∵FM∥CN,EF=FC,
∴FM= CN= ,
故选择:D.
10.D
【详解】
A.∵四边形ABCD是平行四边形
∴
∴
∵O为BD的中点
∴
在与中
∴
∴
∵
∴四边形DEBF为平行四边形,故A选项正确;
B.假设
∵,,
∴
∴
∴
∵
∴
则当时,
∵四边形DEBF为平行四边形
∴四边形DEBF为矩形,故B选项正确;
C.∵,
∴E是AB中点
∵
∴
∵四边形DEBF为平行四边形
∴四边形DEBF为菱形,故C选项正确;
D.当时与时矛盾,则DE不垂直于AB,则四边形DEBF不为矩形,则也不可能为正方形,故D选项错误,
故选:D.
11.3
【详解】
如图所示菱形ABCD,由题意得,
∵,
∴,
在中,
,
OA=,
由勾股定理得即,
解得,
∴.
12.4
【详解】
∵∠ABC=90°,D为斜边AC的中线,
∵AC=8,
∴ ,
故答案为:4.
13.7+2或7﹣2
【详解】
解:由折叠的性质可得:,,,,
∵四边形ABCD是矩形,
∴BC=AD=7,AB=CD=5,AD∥BC,
当点P在线段BC上时,且P、E、D三点在一条直线上时,如图所示:
∴,
∴,
∴,
设,则,
∴在中,,
解得:(不符合题意,舍去);
当点P在线段BC外时,且P、E、D三点在一条直线上时,如图所示:
∴,
∴,
∴,
设,则,
∵,
∴在中,,
解得:(不符合题意,舍去);
∴,
综上所述:当P、E、D三点在一条直线上时,或;
故答案为或.
14.60°
【详解】
解:在矩形ABCD中,∠ADC=90°,
由折叠可知:△DCE≌△DC?E,
∴∠DEC=∠DEC?,∠CDE=∠C?DE,
∵DC?平分∠ADE,
∴∠ADC?=∠C?DE,
∴∠CDE=∠C?DE=∠ADC?,
∵∠CDE+∠C?DE+∠ADC?=∠ADC=90°,
∴∠CDE=∠C?DE=∠ADC?=30°,
∴∠DEC=∠DEC?=90°-30°=60°,
∴ ∠BEC?=180°-∠DEC-∠DEC?=60°,
故答案为:.
15.6
【详解】
如图,作点N关于BD对称的点N′,过点N′作N′M⊥BC于点M,
∴MN′与BD的交点P即满足PM+PN的值最小,
∴MN′=AB·sin∠ABC=4×=6.
故答案为:6.
16.8
【详解】
解:连接CG并延长,交AD于点M,连接EM,作AN⊥EM于N,
∵四边形ABCD为菱形,∠B=60°,
∴AD∥BC,AD=BC=AB
∴∠EAM=120°,∠DMG=∠HCG,
∵G为DH中点,
∴DG=HG,
∵∠MGD=∠CGH,
∴△DMG≌△HCG,
∴DM=HC,CG=MG,
∵H为BC中点,
∴,
∴AM=,
∵E为AB中点,
∴AE=,
∴AE=AM,
∵F为CE中点,G为CM中点,
∴FG为△CEM中位线,
∴,
∵AE=AM,∠EAM=120°,AN⊥EM,
∴EN=EM=,∠AEN=30°,
∴AE=2AN=4,
∴AB=2AE=8.
故答案为:8
17.
【详解】
证明:如图,连接DE,
在正方形ABCD中,AB=AD,∠BAC=∠DAC,
∵在△ABE和△ADE中,
∴△ABE≌△ADE(SAS),
∴BE=DE,
∵EF⊥CD于F,EG⊥AD于G,∠ADC=90°,
∴四边形EFDG是矩形,
∴DE=FG,
∴BE=FG.
18.【详解】
(1)证明:∵四边形ABCD是正方形,
∴∠D=∠BCD=90°,
∴∠ECQ=90°=∠D.
∵E是CD的中点,
∴DE=CE.
又∵∠DEP=∠CEQ,
∴△PDE≌△QCE ;
(2)①证明:①∵PB=PQ,
∴∠PBQ=∠Q,
∵AD∥BC,
∴∠APB=∠PBQ=∠Q=∠EPD,
∵△PDE≌△QCE,
∴PE=QE,
∵PF=BF,
∴是的中位线,
∴EF∥BQ,
∴在Rt△PAB中,AF=PF=BF,
∴∠APF=∠PAF,
∴∠PAF=∠EPD,
∴PE∥AF,
∵EF∥BQ∥AD,
∴四边形AFEP是平行四边形;
②四边形AFEP不是菱形;
理由:
设PD=x,则AP=1-x.由(1)可知△PDE≌△QCE,
∴CQ=PD=x,
∴BQ=BC+CQ=1+x,
∵点E,F分别是PQ,PB的中点,
∴EF是△PBQ的中位线,
∴EF=BQ=,
由①可知AP=EF,即1-x=,
解得:x=,
∴PD=,AP=
在Rt△PDE中,DE=,
则PE==,
∴AP≠PE,
∴四边形AFEP不是菱形.
19.
【详解】
证明:(1)∵平分、平分
∴,
∵∥,
∴,
∴,
∴,,
∴.
(2)∵点为的中点,
∴,又,
∴四边形是平行四边形
∵平分、平分,
∴,
∴
∵,
∴
∵四边形是平行四边形,
∴平行四边形是矩形.
20.
【详解】
(1)证明:∵AC=BC,∠B=60°,
∴△ABC是等边三角形,
∴AB=BC=AC,∠ACB=60°.
∵∠ECF=60°,∴∠ACB=∠ECF,
∴∠ECB=∠ACF.
在△BCE和△ACF中,
∴△BCE≌△ACF(SAS),
∴AF=BE.
(2)证明:由(1)得∠FAC=∠EBC=∠ACB=60°,
∴AF∥BC.
∵AF=BE,AE=DF,
∴AD=AB.
∴AD=BC,
∴四边形ABCD是平行四边形.
∵AB=BC,
∴?ABCD是菱形.
(3)∵△BCE≌△ACF,
∴四边形AFCE的面积=△AFC的面积+△ACE的面积
=△BEC的面积+△ACE的面积
=△ABC的面积,
∵△ABC是一个等边三角形且BC=2,
∴四边形AFCE的面积=×2×2×=3.
21.
【详解】
解:(1)在正方形中,
,
.
又,
在和中,
,,,
,
.
,.
所以菱形是正方形;
(2)如图1,过点作交所在直线于,联结.
,
.
,
.
,
在和中,
,.
.
.
即无论菱形如何变化,点到直线的距离始终为定值1,
;
(3)如图2,当时,
在中,,根据勾股定理得,;
,
在中,根据勾股定理得,,
过点作于,
在中,根据勾股定理得,,
,
为等边三角形.
.
22.(1)t=2;(2)①12≤AQ≤20;②存在这样的t值,使得QE=QB,t的值为3.6或10.
【详解】
(1)如图1,
∵AB∥CD,
∴∠DPA=∠PAB,
由轴对称得:∠DPA=∠EPA,
∴∠EPA=∠PAB,
∴BP=AB=20,
在Rt△PCB中,由勾股定理得:PC==16,
∴PD=4=2t,
∴t=2;
(2)①由(1)可知:当t=2时,Q与B重合,此时AQ=AB=20,
如图2,当PQ⊥AB时,E与Q重合,此时AQ=AD=12,
∴12≤AQ≤20,
故答案为:12≤AQ≤20;
②存在,分两种情况:
当点E在矩形ABCD内部时,如图3,
∵QE=PQ﹣PE=PQ﹣DP=PQ﹣2t,
∵QE=QB,PQ=AQ,
∴QB=AQ﹣2t,
∵AQ+BQ=AB=20,
∴AQ+AQ﹣2t=20,
∴AQ=10+t,
在Rt△EQA中,AQ=10+t,QE=AQ﹣2t=10-t,AE=12,
∴,
解得:t=3.6;
当点E在矩形ABCD的外部时,如图4,
∵QE=PE﹣PQ=DP﹣PQ=2t﹣PQ,
∵QE=QB,PQ=AQ,
∴BQ=2t﹣AQ,
∴AB﹣AQ=2t﹣AQ,
∴AB=2t,
∴t==10(此时P与C重合),
综上,存在这样的t值,使得QE=QB,t的值为3.6或10.
