2020-2021学年九年级数学北师大版下册第一章 解直角三角形的实际应用 同步专题练习题(word版含答案)
文档属性
| 名称 | 2020-2021学年九年级数学北师大版下册第一章 解直角三角形的实际应用 同步专题练习题(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 365.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 00:00:00 | ||
图片预览


文档简介
2020-2021学年北师大版九年级数学下册第一章
解直角三角形的实际应用
同步专题练习题
一、选择题
1.如图,小巷左右两侧是竖直的墙,一架梯子AC斜靠在右墙,测得梯子顶端距离地面AB=2米,梯子与地面夹角α的正弦值sinα=0.8.梯子底端位置不动,将梯子斜靠在左墙时,顶端距离地面2.4米,则小巷的宽度为(
)
A.0.7米
B.1.5米
C.2.2米
D.2.4米
2.如图,钓鱼竿AC长6
m,露在水面上的鱼线BC长3
m,某钓鱼者想看看鱼钓上的情况,把鱼竿AC转动到AC′的位置,此时露在水面上的鱼线B′C′为3
m,则鱼竿转过的角度是(
)
A.60°
B.45°
C.15°
D.90°
3.如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF=27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1∶2.4,那么建筑物AB的高度约为(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)(
)
A.65.8米
B.71.8米
C.73.8米
D.119.8米
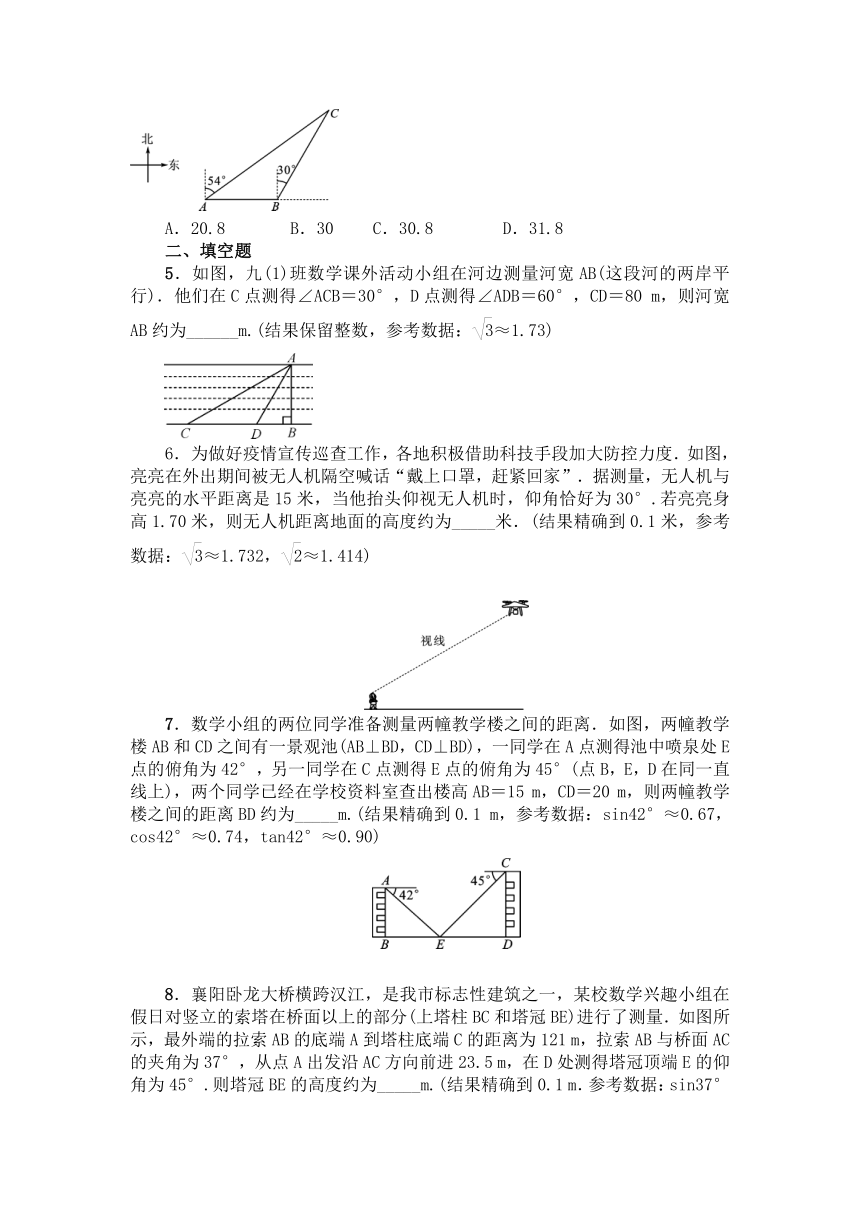
4.我国第一艘国产航空母舰山东舰2019年12月17日在海南三亚某军港交付海军,中国海军正式迈入双航母时代.如图,在一次海上巡航任务中,山东舰由西向东航行,到达A处时,测得小岛C位于它的北偏东54°方向,再航行一段距离到达B处,测得小岛C位于它的北偏东30°方向,且与山东舰相距30海里,则山东舰从A到B航行了(
)海里.(精确到0.1,参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,≈1.73)
A.20.8
B.30
C.30.8
D.31.8
二、填空题
5.如图,九(1)班数学课外活动小组在河边测量河宽AB(这段河的两岸平行).他们在C点测得∠ACB=30°,D点测得∠ADB=60°,CD=80
m,则河宽AB约为______m.(结果保留整数,参考数据:≈1.73)
为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为30°.若亮亮身高1.70米,则无人机距离地面的高度约为_____米.(结果精确到0.1米,参考数据:≈1.732,≈1.414)
7.数学小组的两位同学准备测量两幢教学楼之间的距离.如图,两幢教学楼AB和CD之间有一景观池(AB⊥BD,CD⊥BD),一同学在A点测得池中喷泉处E点的俯角为42°,另一同学在C点测得E点的俯角为45°(点B,E,D在同一直线上),两个同学已经在学校资料室查出楼高AB=15
m,CD=20
m,则两幢教学楼之间的距离BD约为_____m.(结果精确到0.1
m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
8.襄阳卧龙大桥横跨汉江,是我市标志性建筑之一,某校数学兴趣小组在假日对竖立的索塔在桥面以上的部分(上塔柱BC和塔冠BE)进行了测量.如图所示,最外端的拉索AB的底端A到塔柱底端C的距离为121
m,拉索AB与桥面AC的夹角为37°,从点A出发沿AC方向前进23.5
m,在D处测得塔冠顶端E的仰角为45°.则塔冠BE的高度约为_____m.(结果精确到0.1
m.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41).
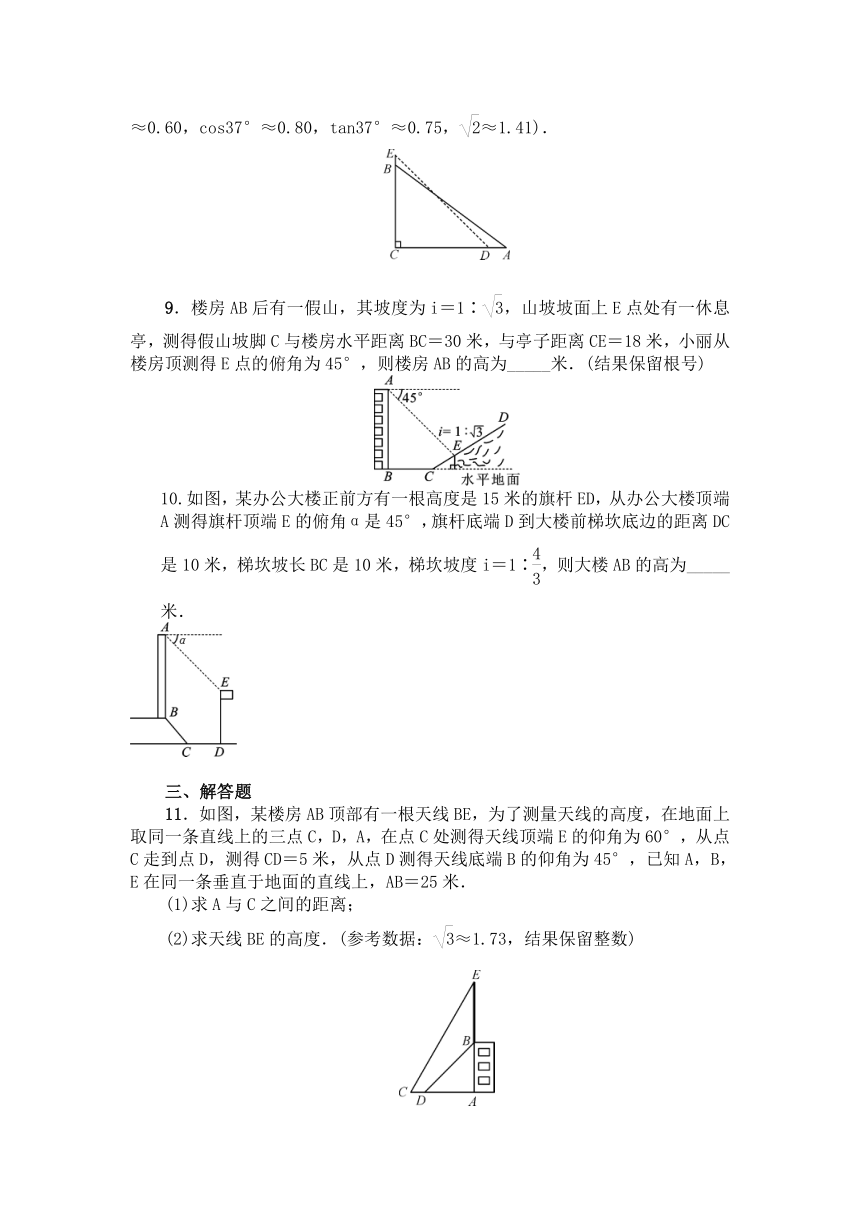
9.楼房AB后有一假山,其坡度为i=1∶,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=30米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°,则楼房AB的高为_____米.(结果保留根号)
10.如图,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是10米,梯坎坡长BC是10米,梯坎坡度i=1∶,则大楼AB的高为_____米.
三、解答题
11.如图,某楼房AB顶部有一根天线BE,为了测量天线的高度,在地面上取同一条直线上的三点C,D,A,在点C处测得天线顶端E的仰角为60°,从点C走到点D,测得CD=5米,从点D测得天线底端B的仰角为45°,已知A,B,E在同一条垂直于地面的直线上,AB=25米.
(1)求A与C之间的距离;
(2)求天线BE的高度.(参考数据:≈1.73,结果保留整数)
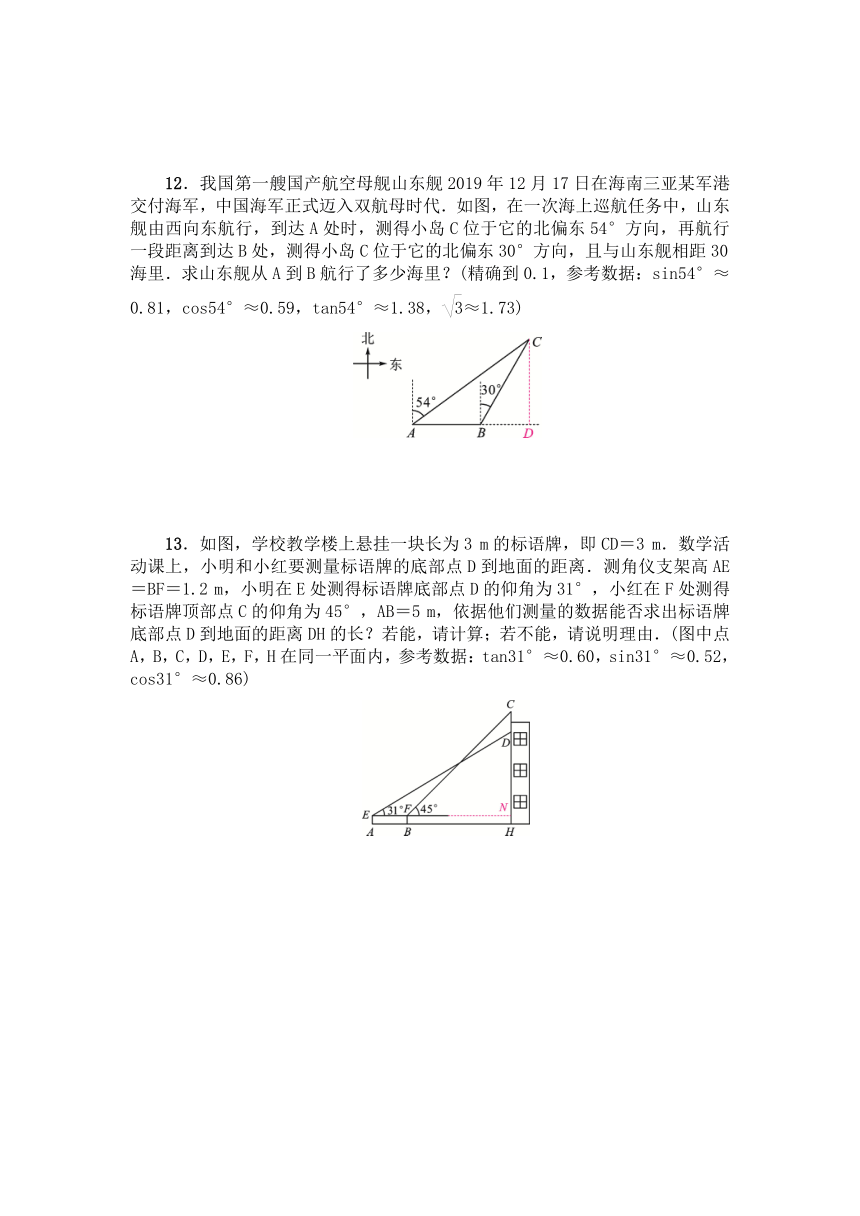
12.我国第一艘国产航空母舰山东舰2019年12月17日在海南三亚某军港交付海军,中国海军正式迈入双航母时代.如图,在一次海上巡航任务中,山东舰由西向东航行,到达A处时,测得小岛C位于它的北偏东54°方向,再航行一段距离到达B处,测得小岛C位于它的北偏东30°方向,且与山东舰相距30海里.求山东舰从A到B航行了多少海里?(精确到0.1,参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,≈1.73)
13.如图,学校教学楼上悬挂一块长为3
m的标语牌,即CD=3
m.数学活动课上,小明和小红要测量标语牌的底部点D到地面的距离.测角仪支架高AE=BF=1.2
m,小明在E处测得标语牌底部点D的仰角为31°,小红在F处测得标语牌顶部点C的仰角为45°,AB=5
m,依据他们测量的数据能否求出标语牌底部点D到地面的距离DH的长?若能,请计算;若不能,请说明理由.(图中点A,B,C,D,E,F,H在同一平面内,参考数据:tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
14.位于河南省登封市境内的元代观星台是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16
m到达点N处,测得点A的仰角为45°,测角仪的高度为1.6
m.
(1)求观星台最高点A距离地面的高度(结果精确到0.1
m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.41);
(2)“景点简介”显示,观星台的高度为12.6
m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.
15.某区域平面示意图如图所示,点D在河的右侧,红军路AB与某桥BC互相垂直.某校“数学兴趣小组”在“研学旅行”活动中,在C处测得点D位于西北方向,又在A处测得点D位于南偏东65°方向,另测得BC=414
m,AB=300
m,求出点D到AB的距离.(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
16.小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米.已知点F,G,D,B在同一水平直线上,且EF,CD,AB均垂直于FB,求这棵古树的高度AB.(小平面镜的大小忽略不计)
参考答案
2020-2021学年北师大版九年级数学下册第一章
解直角三角形的实际应用
同步专题练习题
一、选择题
1.如图,小巷左右两侧是竖直的墙,一架梯子AC斜靠在右墙,测得梯子顶端距离地面AB=2米,梯子与地面夹角α的正弦值sinα=0.8.梯子底端位置不动,将梯子斜靠在左墙时,顶端距离地面2.4米,则小巷的宽度为(C)
A.0.7米
B.1.5米
C.2.2米
D.2.4米
2.如图,钓鱼竿AC长6
m,露在水面上的鱼线BC长3
m,某钓鱼者想看看鱼钓上的情况,把鱼竿AC转动到AC′的位置,此时露在水面上的鱼线B′C′为3
m,则鱼竿转过的角度是(C)
A.60°
B.45°
C.15°
D.90°
3.如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF=27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1∶2.4,那么建筑物AB的高度约为(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)(B)
A.65.8米
B.71.8米
C.73.8米
D.119.8米
4.我国第一艘国产航空母舰山东舰2019年12月17日在海南三亚某军港交付海军,中国海军正式迈入双航母时代.如图,在一次海上巡航任务中,山东舰由西向东航行,到达A处时,测得小岛C位于它的北偏东54°方向,再航行一段距离到达B处,测得小岛C位于它的北偏东30°方向,且与山东舰相距30海里,则山东舰从A到B航行了(A)海里.(精确到0.1,参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,≈1.73)
A.20.8
B.30
C.30.8
D.31.8
二、填空题
5.如图,九(1)班数学课外活动小组在河边测量河宽AB(这段河的两岸平行).他们在C点测得∠ACB=30°,D点测得∠ADB=60°,CD=80
m,则河宽AB约为69m.(结果保留整数,参考数据:≈1.73)
6.为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为30°.若亮亮身高1.70米,则无人机距离地面的高度约为10.4米.(结果精确到0.1米,参考数据:≈1.732,≈1.414)
7.数学小组的两位同学准备测量两幢教学楼之间的距离.如图,两幢教学楼AB和CD之间有一景观池(AB⊥BD,CD⊥BD),一同学在A点测得池中喷泉处E点的俯角为42°,另一同学在C点测得E点的俯角为45°(点B,E,D在同一直线上),两个同学已经在学校资料室查出楼高AB=15
m,CD=20
m,则两幢教学楼之间的距离BD约为36.7m.(结果精确到0.1
m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
8.襄阳卧龙大桥横跨汉江,是我市标志性建筑之一,某校数学兴趣小组在假日对竖立的索塔在桥面以上的部分(上塔柱BC和塔冠BE)进行了测量.如图所示,最外端的拉索AB的底端A到塔柱底端C的距离为121
m,拉索AB与桥面AC的夹角为37°,从点A出发沿AC方向前进23.5
m,在D处测得塔冠顶端E的仰角为45°.则塔冠BE的高度约为6.8m.(结果精确到0.1
m.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41).
9.楼房AB后有一假山,其坡度为i=1∶,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=30米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°,则楼房AB的高为(39+9)米.(结果保留根号)
10.如图,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是10米,梯坎坡长BC是10米,梯坎坡度i=1∶,则大楼AB的高为2米.
三、解答题
11.如图,某楼房AB顶部有一根天线BE,为了测量天线的高度,在地面上取同一条直线上的三点C,D,A,在点C处测得天线顶端E的仰角为60°,从点C走到点D,测得CD=5米,从点D测得天线底端B的仰角为45°,已知A,B,E在同一条垂直于地面的直线上,AB=25米.
(1)求A与C之间的距离;
(2)求天线BE的高度.(参考数据:≈1.73,结果保留整数)
解:(1)∵在Rt△ABD中,∠ADB=45°,
∴AD=AB=25米.
∵CD=5米,
∴AC=AD+CD=25+5=30(米).
答:A与C之间的距离为30米.
(2)在Rt△ACE中,∠C=60°,AC=30米,
∴AE=AC·tanC=30
米.
∵AB=25米,
∴BE=AE-AB=30-25≈27(米).
答:天线BE的高度约为27米.
12.我国第一艘国产航空母舰山东舰2019年12月17日在海南三亚某军港交付海军,中国海军正式迈入双航母时代.如图,在一次海上巡航任务中,山东舰由西向东航行,到达A处时,测得小岛C位于它的北偏东54°方向,再航行一段距离到达B处,测得小岛C位于它的北偏东30°方向,且与山东舰相距30海里.求山东舰从A到B航行了多少海里?(精确到0.1,参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,≈1.73)
解:过C作CD⊥AB交其延长线于点D,
由题可知∠BCD=30°,∠ACD=54°,
在Rt△BCD中,
∵∠BCD=30°,∠BDC=90°,BC=30,
∴BD=15,CD=15.
在Rt△ACD中,
∵∠ACD=54°,∠BDC=90°,CD=15,
tan∠ACD=,
∴AD=CD·tan∠ACD=CD·tan54°≈15×1.38≈35.81(海里).
∴AB=AD-BD=35.81-15=20.81≈20.8(海里).
答:山东舰从A到B航行约20.8海里.
13.如图,学校教学楼上悬挂一块长为3
m的标语牌,即CD=3
m.数学活动课上,小明和小红要测量标语牌的底部点D到地面的距离.测角仪支架高AE=BF=1.2
m,小明在E处测得标语牌底部点D的仰角为31°,小红在F处测得标语牌顶部点C的仰角为45°,AB=5
m,依据他们测量的数据能否求出标语牌底部点D到地面的距离DH的长?若能,请计算;若不能,请说明理由.(图中点A,B,C,D,E,F,H在同一平面内,参考数据:tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
解:能,理由如下:
延长EF交CH于点N,则∠CNF=90°,
∵∠CFN=45°,
∴CN=NF.
设DN=x
m,
则NF=CN=(x+3)m,
∴EN=5+(x+3)=(x+8)m,
在Rt△DEN中,tan∠DEN=,
则DN=EN·tan∠DEN,
∴x≈0.6(x+8),解得x=12.
∴DH=DN+NH=12+1.2=13.2(m).
答:点D到地面的距离DH的长约为13.2
m.
14.位于河南省登封市境内的元代观星台是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16
m到达点N处,测得点A的仰角为45°,测角仪的高度为1.6
m.
(1)求观星台最高点A距离地面的高度(结果精确到0.1
m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.41);
(2)“景点简介”显示,观星台的高度为12.6
m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.
解:(1)过点A作AD⊥PM于点D,延长BC交AD于点E,则四边形BMNC,四边形BMDE是矩形,
∴BC=MN=16
m,DE=CN=BM=1.6
m.
∵∠AEB=90°,∠ACE=45°,
∴△ACE是等腰直角三角形.∴CE=AE.
设AE=CE=x
m,则BE=(16+x)m.
∵∠ABE=22°,∴tan22°==≈0.40.
∴x≈10.7.
∴AD=10.7+1.6=12.3(m).
答:观星台最高点A距离地面的高度约为12.3
m.
(2)∵“景点简介”显示,观星台的高度为12.6
m,
∴本次测量结果的误差为12.6-12.3=0.3(m).
减小误差的合理化建议为:多次测量取平均值.
15.某区域平面示意图如图所示,点D在河的右侧,红军路AB与某桥BC互相垂直.某校“数学兴趣小组”在“研学旅行”活动中,在C处测得点D位于西北方向,又在A处测得点D位于南偏东65°方向,另测得BC=414
m,AB=300
m,求出点D到AB的距离.(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
解:过点D分别作DE⊥AB于点E,DF⊥BC于点F,则四边形EBFD是矩形.
设DE=x,
在Rt△ADE中,∠AED=90°,
∵tan∠DAE=,∴AE==.
∴BE=300-.
又∵BF=DE=x,∴CF=414-x.
在Rt△CDF中,∠DFC=90°,∠DCF=45°,
∴DF=CF=414-x.
又∵BE=DF,∴300-=414-x,
解得x=214.
答:点D到AB的距离是214
m.
16.小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米.已知点F,G,D,B在同一水平直线上,且EF,CD,AB均垂直于FB,求这棵古树的高度AB.(小平面镜的大小忽略不计)
解:过点C作CH⊥AB于点H,则CH=BD,BH=CD=0.5.
在Rt△ACH中,
∠ACH=45°,∴AH=CH=BD.
∴AB=AH+BH=BD+0.5.
∵EF⊥FB,AB⊥FB,∴∠EFG=∠ABG=90°.
由题意,得∠EGF=∠AGB,∴△EFG∽△ABG.
∴=,即=.
解得BD=17.5.
∴AB=17.5+0.5=18(m).
答:这棵古树的高度AB为18
m.
解直角三角形的实际应用
同步专题练习题
一、选择题
1.如图,小巷左右两侧是竖直的墙,一架梯子AC斜靠在右墙,测得梯子顶端距离地面AB=2米,梯子与地面夹角α的正弦值sinα=0.8.梯子底端位置不动,将梯子斜靠在左墙时,顶端距离地面2.4米,则小巷的宽度为(
)
A.0.7米
B.1.5米
C.2.2米
D.2.4米
2.如图,钓鱼竿AC长6
m,露在水面上的鱼线BC长3
m,某钓鱼者想看看鱼钓上的情况,把鱼竿AC转动到AC′的位置,此时露在水面上的鱼线B′C′为3
m,则鱼竿转过的角度是(
)
A.60°
B.45°
C.15°
D.90°
3.如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF=27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1∶2.4,那么建筑物AB的高度约为(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)(
)
A.65.8米
B.71.8米
C.73.8米
D.119.8米
4.我国第一艘国产航空母舰山东舰2019年12月17日在海南三亚某军港交付海军,中国海军正式迈入双航母时代.如图,在一次海上巡航任务中,山东舰由西向东航行,到达A处时,测得小岛C位于它的北偏东54°方向,再航行一段距离到达B处,测得小岛C位于它的北偏东30°方向,且与山东舰相距30海里,则山东舰从A到B航行了(
)海里.(精确到0.1,参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,≈1.73)
A.20.8
B.30
C.30.8
D.31.8
二、填空题
5.如图,九(1)班数学课外活动小组在河边测量河宽AB(这段河的两岸平行).他们在C点测得∠ACB=30°,D点测得∠ADB=60°,CD=80
m,则河宽AB约为______m.(结果保留整数,参考数据:≈1.73)
为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为30°.若亮亮身高1.70米,则无人机距离地面的高度约为_____米.(结果精确到0.1米,参考数据:≈1.732,≈1.414)
7.数学小组的两位同学准备测量两幢教学楼之间的距离.如图,两幢教学楼AB和CD之间有一景观池(AB⊥BD,CD⊥BD),一同学在A点测得池中喷泉处E点的俯角为42°,另一同学在C点测得E点的俯角为45°(点B,E,D在同一直线上),两个同学已经在学校资料室查出楼高AB=15
m,CD=20
m,则两幢教学楼之间的距离BD约为_____m.(结果精确到0.1
m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
8.襄阳卧龙大桥横跨汉江,是我市标志性建筑之一,某校数学兴趣小组在假日对竖立的索塔在桥面以上的部分(上塔柱BC和塔冠BE)进行了测量.如图所示,最外端的拉索AB的底端A到塔柱底端C的距离为121
m,拉索AB与桥面AC的夹角为37°,从点A出发沿AC方向前进23.5
m,在D处测得塔冠顶端E的仰角为45°.则塔冠BE的高度约为_____m.(结果精确到0.1
m.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41).
9.楼房AB后有一假山,其坡度为i=1∶,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=30米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°,则楼房AB的高为_____米.(结果保留根号)
10.如图,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是10米,梯坎坡长BC是10米,梯坎坡度i=1∶,则大楼AB的高为_____米.
三、解答题
11.如图,某楼房AB顶部有一根天线BE,为了测量天线的高度,在地面上取同一条直线上的三点C,D,A,在点C处测得天线顶端E的仰角为60°,从点C走到点D,测得CD=5米,从点D测得天线底端B的仰角为45°,已知A,B,E在同一条垂直于地面的直线上,AB=25米.
(1)求A与C之间的距离;
(2)求天线BE的高度.(参考数据:≈1.73,结果保留整数)
12.我国第一艘国产航空母舰山东舰2019年12月17日在海南三亚某军港交付海军,中国海军正式迈入双航母时代.如图,在一次海上巡航任务中,山东舰由西向东航行,到达A处时,测得小岛C位于它的北偏东54°方向,再航行一段距离到达B处,测得小岛C位于它的北偏东30°方向,且与山东舰相距30海里.求山东舰从A到B航行了多少海里?(精确到0.1,参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,≈1.73)
13.如图,学校教学楼上悬挂一块长为3
m的标语牌,即CD=3
m.数学活动课上,小明和小红要测量标语牌的底部点D到地面的距离.测角仪支架高AE=BF=1.2
m,小明在E处测得标语牌底部点D的仰角为31°,小红在F处测得标语牌顶部点C的仰角为45°,AB=5
m,依据他们测量的数据能否求出标语牌底部点D到地面的距离DH的长?若能,请计算;若不能,请说明理由.(图中点A,B,C,D,E,F,H在同一平面内,参考数据:tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
14.位于河南省登封市境内的元代观星台是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16
m到达点N处,测得点A的仰角为45°,测角仪的高度为1.6
m.
(1)求观星台最高点A距离地面的高度(结果精确到0.1
m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.41);
(2)“景点简介”显示,观星台的高度为12.6
m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.
15.某区域平面示意图如图所示,点D在河的右侧,红军路AB与某桥BC互相垂直.某校“数学兴趣小组”在“研学旅行”活动中,在C处测得点D位于西北方向,又在A处测得点D位于南偏东65°方向,另测得BC=414
m,AB=300
m,求出点D到AB的距离.(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
16.小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米.已知点F,G,D,B在同一水平直线上,且EF,CD,AB均垂直于FB,求这棵古树的高度AB.(小平面镜的大小忽略不计)
参考答案
2020-2021学年北师大版九年级数学下册第一章
解直角三角形的实际应用
同步专题练习题
一、选择题
1.如图,小巷左右两侧是竖直的墙,一架梯子AC斜靠在右墙,测得梯子顶端距离地面AB=2米,梯子与地面夹角α的正弦值sinα=0.8.梯子底端位置不动,将梯子斜靠在左墙时,顶端距离地面2.4米,则小巷的宽度为(C)
A.0.7米
B.1.5米
C.2.2米
D.2.4米
2.如图,钓鱼竿AC长6
m,露在水面上的鱼线BC长3
m,某钓鱼者想看看鱼钓上的情况,把鱼竿AC转动到AC′的位置,此时露在水面上的鱼线B′C′为3
m,则鱼竿转过的角度是(C)
A.60°
B.45°
C.15°
D.90°
3.如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF=27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1∶2.4,那么建筑物AB的高度约为(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)(B)
A.65.8米
B.71.8米
C.73.8米
D.119.8米
4.我国第一艘国产航空母舰山东舰2019年12月17日在海南三亚某军港交付海军,中国海军正式迈入双航母时代.如图,在一次海上巡航任务中,山东舰由西向东航行,到达A处时,测得小岛C位于它的北偏东54°方向,再航行一段距离到达B处,测得小岛C位于它的北偏东30°方向,且与山东舰相距30海里,则山东舰从A到B航行了(A)海里.(精确到0.1,参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,≈1.73)
A.20.8
B.30
C.30.8
D.31.8
二、填空题
5.如图,九(1)班数学课外活动小组在河边测量河宽AB(这段河的两岸平行).他们在C点测得∠ACB=30°,D点测得∠ADB=60°,CD=80
m,则河宽AB约为69m.(结果保留整数,参考数据:≈1.73)
6.为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为30°.若亮亮身高1.70米,则无人机距离地面的高度约为10.4米.(结果精确到0.1米,参考数据:≈1.732,≈1.414)
7.数学小组的两位同学准备测量两幢教学楼之间的距离.如图,两幢教学楼AB和CD之间有一景观池(AB⊥BD,CD⊥BD),一同学在A点测得池中喷泉处E点的俯角为42°,另一同学在C点测得E点的俯角为45°(点B,E,D在同一直线上),两个同学已经在学校资料室查出楼高AB=15
m,CD=20
m,则两幢教学楼之间的距离BD约为36.7m.(结果精确到0.1
m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
8.襄阳卧龙大桥横跨汉江,是我市标志性建筑之一,某校数学兴趣小组在假日对竖立的索塔在桥面以上的部分(上塔柱BC和塔冠BE)进行了测量.如图所示,最外端的拉索AB的底端A到塔柱底端C的距离为121
m,拉索AB与桥面AC的夹角为37°,从点A出发沿AC方向前进23.5
m,在D处测得塔冠顶端E的仰角为45°.则塔冠BE的高度约为6.8m.(结果精确到0.1
m.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41).
9.楼房AB后有一假山,其坡度为i=1∶,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=30米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°,则楼房AB的高为(39+9)米.(结果保留根号)
10.如图,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是10米,梯坎坡长BC是10米,梯坎坡度i=1∶,则大楼AB的高为2米.
三、解答题
11.如图,某楼房AB顶部有一根天线BE,为了测量天线的高度,在地面上取同一条直线上的三点C,D,A,在点C处测得天线顶端E的仰角为60°,从点C走到点D,测得CD=5米,从点D测得天线底端B的仰角为45°,已知A,B,E在同一条垂直于地面的直线上,AB=25米.
(1)求A与C之间的距离;
(2)求天线BE的高度.(参考数据:≈1.73,结果保留整数)
解:(1)∵在Rt△ABD中,∠ADB=45°,
∴AD=AB=25米.
∵CD=5米,
∴AC=AD+CD=25+5=30(米).
答:A与C之间的距离为30米.
(2)在Rt△ACE中,∠C=60°,AC=30米,
∴AE=AC·tanC=30
米.
∵AB=25米,
∴BE=AE-AB=30-25≈27(米).
答:天线BE的高度约为27米.
12.我国第一艘国产航空母舰山东舰2019年12月17日在海南三亚某军港交付海军,中国海军正式迈入双航母时代.如图,在一次海上巡航任务中,山东舰由西向东航行,到达A处时,测得小岛C位于它的北偏东54°方向,再航行一段距离到达B处,测得小岛C位于它的北偏东30°方向,且与山东舰相距30海里.求山东舰从A到B航行了多少海里?(精确到0.1,参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,≈1.73)
解:过C作CD⊥AB交其延长线于点D,
由题可知∠BCD=30°,∠ACD=54°,
在Rt△BCD中,
∵∠BCD=30°,∠BDC=90°,BC=30,
∴BD=15,CD=15.
在Rt△ACD中,
∵∠ACD=54°,∠BDC=90°,CD=15,
tan∠ACD=,
∴AD=CD·tan∠ACD=CD·tan54°≈15×1.38≈35.81(海里).
∴AB=AD-BD=35.81-15=20.81≈20.8(海里).
答:山东舰从A到B航行约20.8海里.
13.如图,学校教学楼上悬挂一块长为3
m的标语牌,即CD=3
m.数学活动课上,小明和小红要测量标语牌的底部点D到地面的距离.测角仪支架高AE=BF=1.2
m,小明在E处测得标语牌底部点D的仰角为31°,小红在F处测得标语牌顶部点C的仰角为45°,AB=5
m,依据他们测量的数据能否求出标语牌底部点D到地面的距离DH的长?若能,请计算;若不能,请说明理由.(图中点A,B,C,D,E,F,H在同一平面内,参考数据:tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
解:能,理由如下:
延长EF交CH于点N,则∠CNF=90°,
∵∠CFN=45°,
∴CN=NF.
设DN=x
m,
则NF=CN=(x+3)m,
∴EN=5+(x+3)=(x+8)m,
在Rt△DEN中,tan∠DEN=,
则DN=EN·tan∠DEN,
∴x≈0.6(x+8),解得x=12.
∴DH=DN+NH=12+1.2=13.2(m).
答:点D到地面的距离DH的长约为13.2
m.
14.位于河南省登封市境内的元代观星台是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16
m到达点N处,测得点A的仰角为45°,测角仪的高度为1.6
m.
(1)求观星台最高点A距离地面的高度(结果精确到0.1
m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.41);
(2)“景点简介”显示,观星台的高度为12.6
m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.
解:(1)过点A作AD⊥PM于点D,延长BC交AD于点E,则四边形BMNC,四边形BMDE是矩形,
∴BC=MN=16
m,DE=CN=BM=1.6
m.
∵∠AEB=90°,∠ACE=45°,
∴△ACE是等腰直角三角形.∴CE=AE.
设AE=CE=x
m,则BE=(16+x)m.
∵∠ABE=22°,∴tan22°==≈0.40.
∴x≈10.7.
∴AD=10.7+1.6=12.3(m).
答:观星台最高点A距离地面的高度约为12.3
m.
(2)∵“景点简介”显示,观星台的高度为12.6
m,
∴本次测量结果的误差为12.6-12.3=0.3(m).
减小误差的合理化建议为:多次测量取平均值.
15.某区域平面示意图如图所示,点D在河的右侧,红军路AB与某桥BC互相垂直.某校“数学兴趣小组”在“研学旅行”活动中,在C处测得点D位于西北方向,又在A处测得点D位于南偏东65°方向,另测得BC=414
m,AB=300
m,求出点D到AB的距离.(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
解:过点D分别作DE⊥AB于点E,DF⊥BC于点F,则四边形EBFD是矩形.
设DE=x,
在Rt△ADE中,∠AED=90°,
∵tan∠DAE=,∴AE==.
∴BE=300-.
又∵BF=DE=x,∴CF=414-x.
在Rt△CDF中,∠DFC=90°,∠DCF=45°,
∴DF=CF=414-x.
又∵BE=DF,∴300-=414-x,
解得x=214.
答:点D到AB的距离是214
m.
16.小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米.已知点F,G,D,B在同一水平直线上,且EF,CD,AB均垂直于FB,求这棵古树的高度AB.(小平面镜的大小忽略不计)
解:过点C作CH⊥AB于点H,则CH=BD,BH=CD=0.5.
在Rt△ACH中,
∠ACH=45°,∴AH=CH=BD.
∴AB=AH+BH=BD+0.5.
∵EF⊥FB,AB⊥FB,∴∠EFG=∠ABG=90°.
由题意,得∠EGF=∠AGB,∴△EFG∽△ABG.
∴=,即=.
解得BD=17.5.
∴AB=17.5+0.5=18(m).
答:这棵古树的高度AB为18
m.
