2020-2021学年北师大版数学九年级下册 第三章 圆 3.9 弧长及扇形的面积 复习练习(word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版数学九年级下册 第三章 圆 3.9 弧长及扇形的面积 复习练习(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 215.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 06:45:32 | ||
图片预览


文档简介
第三章 圆 3.9 弧长及扇形的面积
1.在半径为6的⊙O中,60°圆心角所对的弧长是( )
A.π B.2π C.4π D.6π
2.一个扇形的半径为8cm,弧长为πcm,则扇形的圆心角为( )
A.60° B.120° C.150° D.180°
3.如图,?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则的长为( )
A.π B.π C.π D.π
4.钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是( )
A.π B.π C.π D.π
5. 如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2,将△ABC绕直角顶点C逆时针旋转60°得△A′B′C′,则点B转过的路径长为( )
A. B. C. D.π
6.已知40°的圆心角所对应的扇形面积为π cm2,则这条弧所在圆的直径为( )
A.2 cm B.4 cm C.8 cm D.16 cm
7.如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则的长为( )
A.π B.6π C.3π D.1.5π
8.如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,则点B在两次旋转过程中经过的路径的长是( )
A.π B.13π C.25π D.25
9.如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则的长度为 .
10.如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是 (结果保留π).
11.如图,四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是 .
12.如图,⊙O的半径为2,点A、B在⊙O上,∠AOB=90°,则阴影部分的面积为 .
13. 75°的圆心角所对的弧长是2.5πcm,则此弧所在圆的半径是 cm.
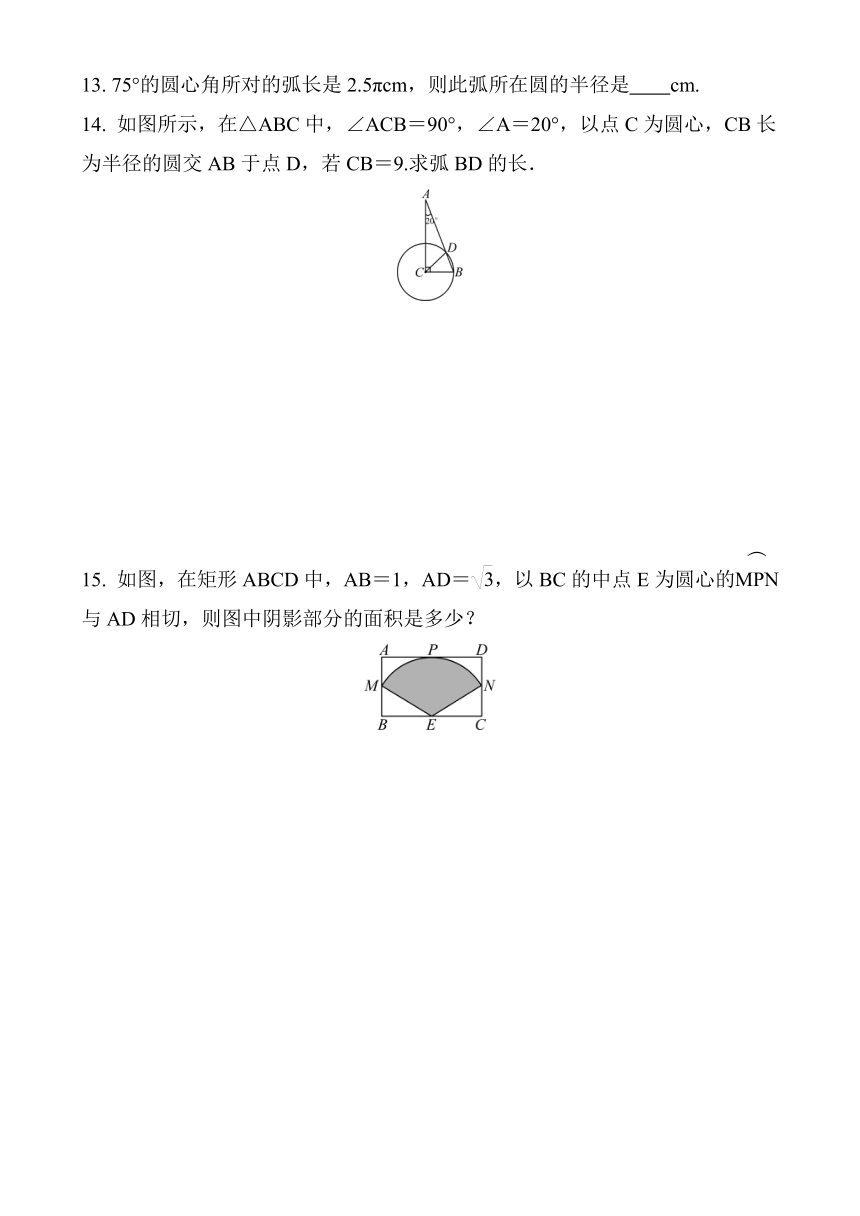
14. 如图所示,在△ABC中,∠ACB=90°,∠A=20°,以点C为圆心,CB长为半径的圆交AB于点D,若CB=9.求弧BD的长.
如图,在矩形ABCD中,AB=1,AD=,以BC的中点E为圆心的与AD相切,则图中阴影部分的面积是多少?
17.如图,已知菱形ABCD的边长为3cm,B、C两点在扇形AEF的上.求的长度及扇形ABC的面积.
18.如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为的中点,连接DE、EB.
(1)求证:四边形BCDE是平行四边形;
(2)已知图中阴影部分的面积为6π,求⊙O的半径r.
19. 如图,四边形ABCD是正方形,以边AB为直径作⊙O,点E在BC边上,连接AE交⊙O于点F,连接BF,并延长交CD于点G.
(1)求证:△ABE≌△BCG;
(2)若∠AEB=55°,OA=3,求的长.(结果保留π)
答案:
1-8 BBBAB CDA
9. π
10. 3-
11. 6π
12. π-2
13. 6
14. 解: 由图及题意可知,CB=CD.∵∠A=20°,∠ACB=90°,
∴∠CBD=∠CDB=180°-90°-20°=70°,
∴∠BCD=180°-70°-70°=40°.
∴弧BD的长===2π.
16. 解: ∵BC=AD=,∴BE=.连接PE,∵AD切⊙E于P点,∴PE⊥AD,∵∠A=∠B=90°,∴四边形ABEP为矩形,∴PE=AB=1.
在Rt△BEM中,==,∴∠BEM=30°,同理∠CEN=30°,
∴∠MEN=180°-30°×2=120°.∴S扇形===.
17. 解:∵四边形ABCD是菱形且边长为3cm,∴AB=BC=3cm.又∵B、C两点在扇形AEF的上,∴AB=BC=AC=3cm,∴△ABC是等边三角形,∴∠BAC=60°,的长l==π(cm).S扇形ABC=lR=×π×3=π(cm2).
18. (1) 证明:∵∠BOD=60°,∴∠AOD=120°,∴=,∵E为的中点,∴==,∴DE∥AB,OD⊥BE,即DE∥BC,∵CD是⊙O的切线,∴OD⊥CD,∴BE∥CD,∴四边形BCDE是平行四边形;
(2) 解:连接OE,由(1)知,==,∴∠BOE=120°,
∵阴影部分面积为6π,∴=6π,∴r=6.
19. (1)证明:∵四边形ABCD是正方形,AB为⊙O的直径,∴∠ABE=∠BCG=∠AFB=90°,∴∠BAF+∠ABF=90°,∠ABF+∠EBF=90°,∴∠EBF=∠BAF,在△ABE与△BCG中,,
∴△ABE≌△BCG(ASA);
(2)解:连接OF,∵∠ABE=∠AFB=90°,∠AEB=55°,
∴∠BAE=90°-55°=35°,∴∠BOF=2∠BAE=70°,
∵OA=3,∴的长==.
1.在半径为6的⊙O中,60°圆心角所对的弧长是( )
A.π B.2π C.4π D.6π
2.一个扇形的半径为8cm,弧长为πcm,则扇形的圆心角为( )
A.60° B.120° C.150° D.180°
3.如图,?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则的长为( )
A.π B.π C.π D.π
4.钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是( )
A.π B.π C.π D.π
5. 如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2,将△ABC绕直角顶点C逆时针旋转60°得△A′B′C′,则点B转过的路径长为( )
A. B. C. D.π
6.已知40°的圆心角所对应的扇形面积为π cm2,则这条弧所在圆的直径为( )
A.2 cm B.4 cm C.8 cm D.16 cm
7.如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则的长为( )
A.π B.6π C.3π D.1.5π
8.如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,则点B在两次旋转过程中经过的路径的长是( )
A.π B.13π C.25π D.25
9.如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AB长为半径画圆弧交边DC于点E,则的长度为 .
10.如图,在?ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是 (结果保留π).
11.如图,四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是 .
12.如图,⊙O的半径为2,点A、B在⊙O上,∠AOB=90°,则阴影部分的面积为 .
13. 75°的圆心角所对的弧长是2.5πcm,则此弧所在圆的半径是 cm.
14. 如图所示,在△ABC中,∠ACB=90°,∠A=20°,以点C为圆心,CB长为半径的圆交AB于点D,若CB=9.求弧BD的长.
如图,在矩形ABCD中,AB=1,AD=,以BC的中点E为圆心的与AD相切,则图中阴影部分的面积是多少?
17.如图,已知菱形ABCD的边长为3cm,B、C两点在扇形AEF的上.求的长度及扇形ABC的面积.
18.如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为的中点,连接DE、EB.
(1)求证:四边形BCDE是平行四边形;
(2)已知图中阴影部分的面积为6π,求⊙O的半径r.
19. 如图,四边形ABCD是正方形,以边AB为直径作⊙O,点E在BC边上,连接AE交⊙O于点F,连接BF,并延长交CD于点G.
(1)求证:△ABE≌△BCG;
(2)若∠AEB=55°,OA=3,求的长.(结果保留π)
答案:
1-8 BBBAB CDA
9. π
10. 3-
11. 6π
12. π-2
13. 6
14. 解: 由图及题意可知,CB=CD.∵∠A=20°,∠ACB=90°,
∴∠CBD=∠CDB=180°-90°-20°=70°,
∴∠BCD=180°-70°-70°=40°.
∴弧BD的长===2π.
16. 解: ∵BC=AD=,∴BE=.连接PE,∵AD切⊙E于P点,∴PE⊥AD,∵∠A=∠B=90°,∴四边形ABEP为矩形,∴PE=AB=1.
在Rt△BEM中,==,∴∠BEM=30°,同理∠CEN=30°,
∴∠MEN=180°-30°×2=120°.∴S扇形===.
17. 解:∵四边形ABCD是菱形且边长为3cm,∴AB=BC=3cm.又∵B、C两点在扇形AEF的上,∴AB=BC=AC=3cm,∴△ABC是等边三角形,∴∠BAC=60°,的长l==π(cm).S扇形ABC=lR=×π×3=π(cm2).
18. (1) 证明:∵∠BOD=60°,∴∠AOD=120°,∴=,∵E为的中点,∴==,∴DE∥AB,OD⊥BE,即DE∥BC,∵CD是⊙O的切线,∴OD⊥CD,∴BE∥CD,∴四边形BCDE是平行四边形;
(2) 解:连接OE,由(1)知,==,∴∠BOE=120°,
∵阴影部分面积为6π,∴=6π,∴r=6.
19. (1)证明:∵四边形ABCD是正方形,AB为⊙O的直径,∴∠ABE=∠BCG=∠AFB=90°,∴∠BAF+∠ABF=90°,∠ABF+∠EBF=90°,∴∠EBF=∠BAF,在△ABE与△BCG中,,
∴△ABE≌△BCG(ASA);
(2)解:连接OF,∵∠ABE=∠AFB=90°,∠AEB=55°,
∴∠BAE=90°-55°=35°,∴∠BOF=2∠BAE=70°,
∵OA=3,∴的长==.
