2020-2021学年北师大版九年级数学下册第一章 1.2-1.3同步练习题(Word版,附答案)
文档属性
| 名称 | 2020-2021学年北师大版九年级数学下册第一章 1.2-1.3同步练习题(Word版,附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 220.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 23:58:52 | ||
图片预览




文档简介
2020-2021学年北师大版九年级数学下册第一章
1.2-1.3
同步练习题
一、选择题
1、在△ABC中,若∠C=90°,cosA=,则∠A=(
)
A.20°
B.30°
C.45°
D.60°
2、已知α是锐角,sinα=cos60°,则α等于(
)
A.30°
B.45°
C.60°
D.不能确定
3、已知α为锐角,且满足tan(α+10°)=1,则α为(
)度.
A.10°
B.20°
C.25°
D.15°
4、如图,在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,CD=40,则AB=(
).
A.40+40.
B.40-40.
C.20+40.
D.20-40.
5、如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕.若AE=3,则sin∠BFD的值为(
)
A.1
B.1.5
C.
D.2
二、填空题
6、sin60°=_____.
7、计算:
(1)2sin30°+3cos60°-4tan45°=_____.
(2)+tan260°=_____.
8、在△ABC中,若(cosA-)2+|1-tanB|=0,则∠C=_____.
9、计算:=_____.
10、如图,在由10个完全相同的正三角形构成的网格图中,∠α,∠β如图所示,则cos(α+β)=_____.
11、如图所示,∠AOB是放置在正方形网格中的一个角,则sin∠AOB的值是_____.
12、如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么sin∠EFC的值为_____.
13、一般地,当α,β为任意角时,sin(α+β)与sin(α-β)的值可以用下面的公式求得:sin(α+β)=sinα·cosβ+cosα·sinβ;sin(α-β)=sinα·cosβ-cosα·sinβ.例如sin75°=sin(45°+30°)=sin45°·cos30°+cos45°·sin30°=×+×=.类似地,可以求得sin15°的值是_____.
三、解答题
14、计算:2cos60°+4sin60°-tan30°-cos245°.
15、如图所示,在△ABC中,∠C=90°,sinA=,AB=15,求△ABC的周长和tanA的值.
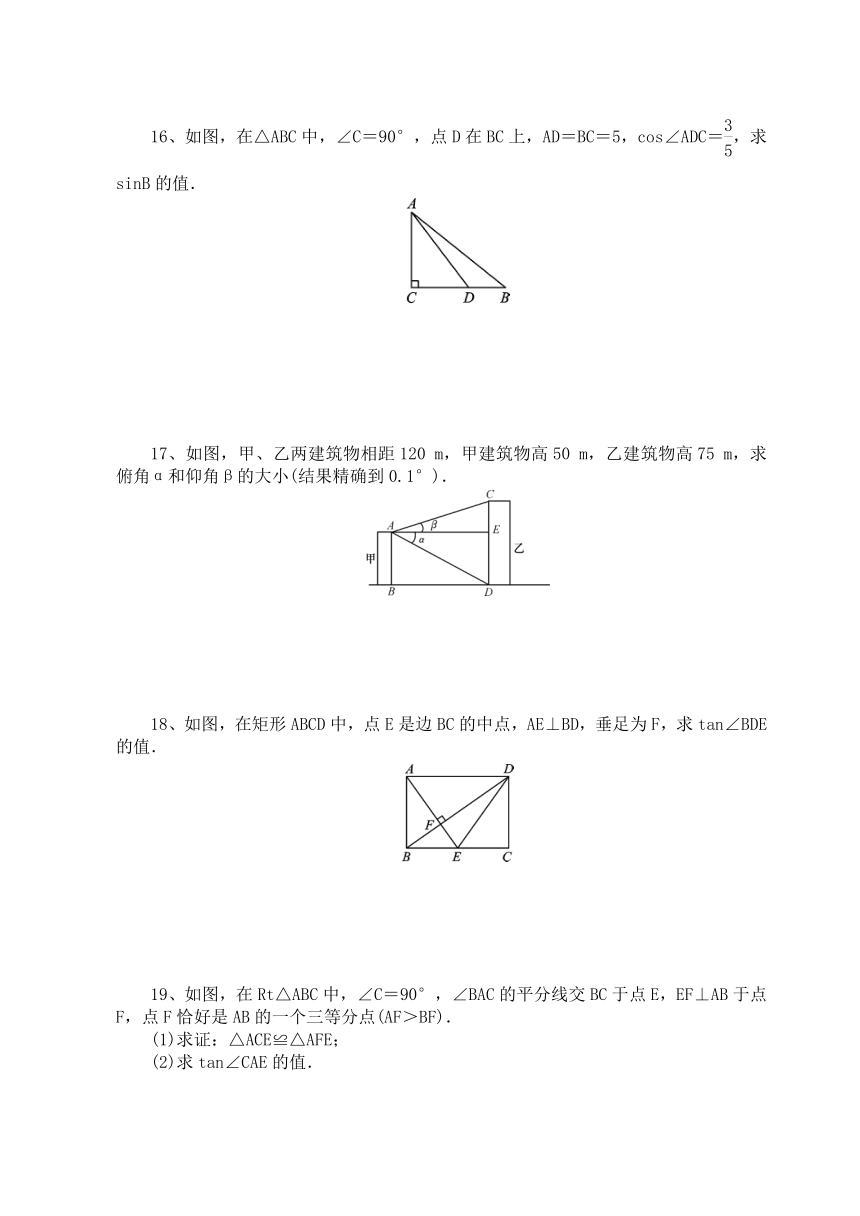
16、如图,在△ABC中,∠C=90°,点D在BC上,AD=BC=5,cos∠ADC=,求sinB的值.
17、如图,甲、乙两建筑物相距120
m,甲建筑物高50
m,乙建筑物高75
m,求俯角α和仰角β的大小(结果精确到0.1°).
18、如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,求tan∠BDE的值.
19、如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).
(1)求证:△ACE≌△AFE;
(2)求tan∠CAE的值.
20、如图,在△ABC中,∠B=30°,∠ADC=45°,∠ACB=120°,D是BC上一点.若CD=8,求BD的长.
21、如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C,D为监测点,已知点C,D,B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°.
(1)求道路AB段的长(结果精确到1米);
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由.
22、京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A,B和点C,D,先用卷尺量出AB=180
m,CD=60
m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
23、如图所示,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10
m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9
s,已知∠B=30°,∠C=45°.
(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80
km/h,那么这辆汽车是否超速?请说明理由.(参考数据:≈1.7,≈1.4)
24、如图,2号楼在1号楼的左侧,两楼高度均为90
m,楼间距为AB,冬至日正午,太阳光线与水平面所成的角为32.3°,1号楼在2号楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,1号楼在2号楼墙面上的影高为DA.已知CD=42
m.求楼间距AB的长度为多少米?(结果精确到1
m)
参考答案
2020-2021学年北师大版九年级数学下册第一章
1.2-1.3同步练习题
一、选择题
1、在△ABC中,若∠C=90°,cosA=,则∠A=(C)
A.20°
B.30°
C.45°
D.60°
2、已知α是锐角,sinα=cos60°,则α等于(A)
A.30°
B.45°
C.60°
D.不能确定
3、已知α为锐角,且满足tan(α+10°)=1,则α为(B)度.
A.10°
B.20°
C.25°
D.15°
4、如图,在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,CD=40,则AB=(A).
A.40+40.
B.40-40.
C.20+40.
D.20-40.
5、如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕.若AE=3,则sin∠BFD的值为(
C
)
A.1
B.1.5
C.
D.2
二、填空题
6、sin60°=.
7、计算:
(1)2sin30°+3cos60°-4tan45°=-;
+tan260°=.
8、在△ABC中,若(cosA-)2+|1-tanB|=0,则∠C=75°.
9、计算:=3+.
10、如图,在由10个完全相同的正三角形构成的网格图中,∠α,∠β如图所示,则cos(α+β)=.
11、如图所示,∠AOB是放置在正方形网格中的一个角,则sin∠AOB的值是.
12、如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么sin∠EFC的值为.
13、一般地,当α,β为任意角时,sin(α+β)与sin(α-β)的值可以用下面的公式求得:sin(α+β)=sinα·cosβ+cosα·sinβ;sin(α-β)=sinα·cosβ-cosα·sinβ.例如sin75°=sin(45°+30°)=sin45°·cos30°+cos45°·sin30°=×+×=.类似地,可以求得sin15°的值是.
三、解答题
14、计算:2cos60°+4sin60°-tan30°-cos245°.
解:原式=2×+4×--()2
=1+2--
=+.
15、如图所示,在△ABC中,∠C=90°,sinA=,AB=15,求△ABC的周长和tanA的值.
解:∵sinA==,AB=15,
∴BC=AB=×15=12.
∴AC==9.
∴△ABC的周长为9+12+15=36,
tanA===.
16、如图,在△ABC中,∠C=90°,点D在BC上,AD=BC=5,cos∠ADC=,求sinB的值.
解:∵AD=5,cos∠ADC=,
∴CD=3.
在Rt△ACD中,∵AD=5,CD=3,
∴AC===4.
在Rt△ACB中,∵AC=4,BC=5,
∴AB===.
∴sinB===.
17、如图,甲、乙两建筑物相距120
m,甲建筑物高50
m,乙建筑物高75
m,求俯角α和仰角β的大小(结果精确到0.1°).
解:∵AB=50,CD=75,BD=120,
∴DE=50,CE=CD-DE=75-50=25,AE=120.
∴tanα===,tanβ===.
∴α≈22.6°,β≈11.8°.
答:俯角α约为22.6°,仰角β约为11.8°.
18、如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,求tan∠BDE的值.
解:∵四边形ABCD是矩形,
∴AD=BC,AB=CD,AD∥BC.
∴△BEF∽△DAF.
∴=.
∵点E是边BC的中点,
∴BE=BC=AD.
∴EF=AF.∴EF=AE.
∵AB=CD,∠ABE=∠C=90°,BE=CE,
∴△ABE≌△DCE(SAS).
∴AE=DE.
设EF=x,则DE=3x.
∴DF==2x.
∴tan∠BDE===.
19、如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).
(1)求证:△ACE≌△AFE;
(2)求tan∠CAE的值.
解:(1)证明:∵AE是∠BAC的平分线,EC⊥AC,EF⊥AF,
∴CE=EF.
在Rt△ACE和Rt△AFE中,
∴Rt△ACE≌Rt△AFE(HL).
(2)由(1)可知△ACE≌△AFE,
∴AC=AF.
设BF=m,则AC=AF=2m,∴AB=3m.
∴BC===m.
∴在Rt△ABC中,tanB===.
在Rt△EFB中,EF=BF·tanB=,
∴CE=EF=.
∴在Rt△ACE中,tan∠CAE===.
20、如图,在△ABC中,∠B=30°,∠ADC=45°,∠ACB=120°,D是BC上一点.若CD=8,求BD的长.
解:过点A作AE⊥BC交BC的延长线于点E.
∵∠ACB=120°,∴∠ACE=60°.
设EC=x,则AE=EC·tan60°=x.
∵∠ADC=45°,∴DE=AE.
∴8+x=x,解得x=4+4.
∵∠B=30°,∴BE==AE=3x.
∴BD=BE-DC-CE=3x-8-x=2x-8=8.
21、如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C,D为监测点,已知点C,D,B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°.
(1)求道路AB段的长(结果精确到1米);
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由.
解:(1)在Rt△ACD中,
AC=CD·tan∠ADC=400×2=800(米).
在Rt△ABC中,AB==≈1
395(米).
(2)该车没有超速,理由如下:
∵车速为=15.5(米/秒)=55.8(千米/时)<60(千米/时),
∴该车没有超速.
22、京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A,B和点C,D,先用卷尺量出AB=180
m,CD=60
m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
解:过点D作DE⊥AB于点E,可得四边形CHED为矩形,
∴HE=CD=60
m.
设CH=DE=x
m,
在Rt△BDE中,∠DBA=60°,
∴BE==x
m.
在Rt△ACH中,∠BAC=30°,
∴AH==x
m.
由AH+HE+EB=AB=180
m,得
x+60+x=180.
解得x=30,即CH=30
m.
答:该段运河的河宽为30
m.
23、如图所示,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10
m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9
s,已知∠B=30°,∠C=45°.
(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80
km/h,那么这辆汽车是否超速?请说明理由.(参考数据:≈1.7,≈1.4)
解:(1)过点A作AD⊥BC于点D,则AD=10
m.
在Rt△ACD中,
∵∠C=45°,
∴AD=CD=10
m.
在Rt△ABD中,∵∠B=30°,
∴BD==AD=10
m.
∴BC=BD+DC=(10+10)m,
即B,C之间的距离为(10+10)m.
(2)这辆汽车超速.理由如下:
∵BC=10+10≈27(m),
∴汽车速度为=30(m/s)=108(km/h).
∵108>80,
∴这辆汽车超速.
24、如图,2号楼在1号楼的左侧,两楼高度均为90
m,楼间距为AB,冬至日正午,太阳光线与水平面所成的角为32.3°,1号楼在2号楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,1号楼在2号楼墙面上的影高为DA.已知CD=42
m.求楼间距AB的长度为多少米?(结果精确到1
m)
解:过点C作CM⊥BE于点M,过点D作DN⊥BE于点N.
则四边形CDNM,ABND是矩形.
∴CD=MN,AB=DN=CM.
在Rt△CEM中,
∵tan∠ECM=,
∴EM=CM·tan32.3°.
在Rt△DEN中,∵tan∠EDN=,
∴EN=DN·tan55.7°.
∵MN=EN-EM,
∴42=AB·tan55.7°-AB·tan32.3°,
解得AB≈50.
答:楼间距AB的长度约为50
m.
1.2-1.3
同步练习题
一、选择题
1、在△ABC中,若∠C=90°,cosA=,则∠A=(
)
A.20°
B.30°
C.45°
D.60°
2、已知α是锐角,sinα=cos60°,则α等于(
)
A.30°
B.45°
C.60°
D.不能确定
3、已知α为锐角,且满足tan(α+10°)=1,则α为(
)度.
A.10°
B.20°
C.25°
D.15°
4、如图,在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,CD=40,则AB=(
).
A.40+40.
B.40-40.
C.20+40.
D.20-40.
5、如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕.若AE=3,则sin∠BFD的值为(
)
A.1
B.1.5
C.
D.2
二、填空题
6、sin60°=_____.
7、计算:
(1)2sin30°+3cos60°-4tan45°=_____.
(2)+tan260°=_____.
8、在△ABC中,若(cosA-)2+|1-tanB|=0,则∠C=_____.
9、计算:=_____.
10、如图,在由10个完全相同的正三角形构成的网格图中,∠α,∠β如图所示,则cos(α+β)=_____.
11、如图所示,∠AOB是放置在正方形网格中的一个角,则sin∠AOB的值是_____.
12、如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么sin∠EFC的值为_____.
13、一般地,当α,β为任意角时,sin(α+β)与sin(α-β)的值可以用下面的公式求得:sin(α+β)=sinα·cosβ+cosα·sinβ;sin(α-β)=sinα·cosβ-cosα·sinβ.例如sin75°=sin(45°+30°)=sin45°·cos30°+cos45°·sin30°=×+×=.类似地,可以求得sin15°的值是_____.
三、解答题
14、计算:2cos60°+4sin60°-tan30°-cos245°.
15、如图所示,在△ABC中,∠C=90°,sinA=,AB=15,求△ABC的周长和tanA的值.
16、如图,在△ABC中,∠C=90°,点D在BC上,AD=BC=5,cos∠ADC=,求sinB的值.
17、如图,甲、乙两建筑物相距120
m,甲建筑物高50
m,乙建筑物高75
m,求俯角α和仰角β的大小(结果精确到0.1°).
18、如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,求tan∠BDE的值.
19、如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).
(1)求证:△ACE≌△AFE;
(2)求tan∠CAE的值.
20、如图,在△ABC中,∠B=30°,∠ADC=45°,∠ACB=120°,D是BC上一点.若CD=8,求BD的长.
21、如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C,D为监测点,已知点C,D,B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°.
(1)求道路AB段的长(结果精确到1米);
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由.
22、京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A,B和点C,D,先用卷尺量出AB=180
m,CD=60
m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
23、如图所示,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10
m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9
s,已知∠B=30°,∠C=45°.
(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80
km/h,那么这辆汽车是否超速?请说明理由.(参考数据:≈1.7,≈1.4)
24、如图,2号楼在1号楼的左侧,两楼高度均为90
m,楼间距为AB,冬至日正午,太阳光线与水平面所成的角为32.3°,1号楼在2号楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,1号楼在2号楼墙面上的影高为DA.已知CD=42
m.求楼间距AB的长度为多少米?(结果精确到1
m)
参考答案
2020-2021学年北师大版九年级数学下册第一章
1.2-1.3同步练习题
一、选择题
1、在△ABC中,若∠C=90°,cosA=,则∠A=(C)
A.20°
B.30°
C.45°
D.60°
2、已知α是锐角,sinα=cos60°,则α等于(A)
A.30°
B.45°
C.60°
D.不能确定
3、已知α为锐角,且满足tan(α+10°)=1,则α为(B)度.
A.10°
B.20°
C.25°
D.15°
4、如图,在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,CD=40,则AB=(A).
A.40+40.
B.40-40.
C.20+40.
D.20-40.
5、如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕.若AE=3,则sin∠BFD的值为(
C
)
A.1
B.1.5
C.
D.2
二、填空题
6、sin60°=.
7、计算:
(1)2sin30°+3cos60°-4tan45°=-;
+tan260°=.
8、在△ABC中,若(cosA-)2+|1-tanB|=0,则∠C=75°.
9、计算:=3+.
10、如图,在由10个完全相同的正三角形构成的网格图中,∠α,∠β如图所示,则cos(α+β)=.
11、如图所示,∠AOB是放置在正方形网格中的一个角,则sin∠AOB的值是.
12、如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么sin∠EFC的值为.
13、一般地,当α,β为任意角时,sin(α+β)与sin(α-β)的值可以用下面的公式求得:sin(α+β)=sinα·cosβ+cosα·sinβ;sin(α-β)=sinα·cosβ-cosα·sinβ.例如sin75°=sin(45°+30°)=sin45°·cos30°+cos45°·sin30°=×+×=.类似地,可以求得sin15°的值是.
三、解答题
14、计算:2cos60°+4sin60°-tan30°-cos245°.
解:原式=2×+4×--()2
=1+2--
=+.
15、如图所示,在△ABC中,∠C=90°,sinA=,AB=15,求△ABC的周长和tanA的值.
解:∵sinA==,AB=15,
∴BC=AB=×15=12.
∴AC==9.
∴△ABC的周长为9+12+15=36,
tanA===.
16、如图,在△ABC中,∠C=90°,点D在BC上,AD=BC=5,cos∠ADC=,求sinB的值.
解:∵AD=5,cos∠ADC=,
∴CD=3.
在Rt△ACD中,∵AD=5,CD=3,
∴AC===4.
在Rt△ACB中,∵AC=4,BC=5,
∴AB===.
∴sinB===.
17、如图,甲、乙两建筑物相距120
m,甲建筑物高50
m,乙建筑物高75
m,求俯角α和仰角β的大小(结果精确到0.1°).
解:∵AB=50,CD=75,BD=120,
∴DE=50,CE=CD-DE=75-50=25,AE=120.
∴tanα===,tanβ===.
∴α≈22.6°,β≈11.8°.
答:俯角α约为22.6°,仰角β约为11.8°.
18、如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,求tan∠BDE的值.
解:∵四边形ABCD是矩形,
∴AD=BC,AB=CD,AD∥BC.
∴△BEF∽△DAF.
∴=.
∵点E是边BC的中点,
∴BE=BC=AD.
∴EF=AF.∴EF=AE.
∵AB=CD,∠ABE=∠C=90°,BE=CE,
∴△ABE≌△DCE(SAS).
∴AE=DE.
设EF=x,则DE=3x.
∴DF==2x.
∴tan∠BDE===.
19、如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).
(1)求证:△ACE≌△AFE;
(2)求tan∠CAE的值.
解:(1)证明:∵AE是∠BAC的平分线,EC⊥AC,EF⊥AF,
∴CE=EF.
在Rt△ACE和Rt△AFE中,
∴Rt△ACE≌Rt△AFE(HL).
(2)由(1)可知△ACE≌△AFE,
∴AC=AF.
设BF=m,则AC=AF=2m,∴AB=3m.
∴BC===m.
∴在Rt△ABC中,tanB===.
在Rt△EFB中,EF=BF·tanB=,
∴CE=EF=.
∴在Rt△ACE中,tan∠CAE===.
20、如图,在△ABC中,∠B=30°,∠ADC=45°,∠ACB=120°,D是BC上一点.若CD=8,求BD的长.
解:过点A作AE⊥BC交BC的延长线于点E.
∵∠ACB=120°,∴∠ACE=60°.
设EC=x,则AE=EC·tan60°=x.
∵∠ADC=45°,∴DE=AE.
∴8+x=x,解得x=4+4.
∵∠B=30°,∴BE==AE=3x.
∴BD=BE-DC-CE=3x-8-x=2x-8=8.
21、如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C,D为监测点,已知点C,D,B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°.
(1)求道路AB段的长(结果精确到1米);
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由.
解:(1)在Rt△ACD中,
AC=CD·tan∠ADC=400×2=800(米).
在Rt△ABC中,AB==≈1
395(米).
(2)该车没有超速,理由如下:
∵车速为=15.5(米/秒)=55.8(千米/时)<60(千米/时),
∴该车没有超速.
22、京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A,B和点C,D,先用卷尺量出AB=180
m,CD=60
m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
解:过点D作DE⊥AB于点E,可得四边形CHED为矩形,
∴HE=CD=60
m.
设CH=DE=x
m,
在Rt△BDE中,∠DBA=60°,
∴BE==x
m.
在Rt△ACH中,∠BAC=30°,
∴AH==x
m.
由AH+HE+EB=AB=180
m,得
x+60+x=180.
解得x=30,即CH=30
m.
答:该段运河的河宽为30
m.
23、如图所示,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10
m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9
s,已知∠B=30°,∠C=45°.
(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80
km/h,那么这辆汽车是否超速?请说明理由.(参考数据:≈1.7,≈1.4)
解:(1)过点A作AD⊥BC于点D,则AD=10
m.
在Rt△ACD中,
∵∠C=45°,
∴AD=CD=10
m.
在Rt△ABD中,∵∠B=30°,
∴BD==AD=10
m.
∴BC=BD+DC=(10+10)m,
即B,C之间的距离为(10+10)m.
(2)这辆汽车超速.理由如下:
∵BC=10+10≈27(m),
∴汽车速度为=30(m/s)=108(km/h).
∵108>80,
∴这辆汽车超速.
24、如图,2号楼在1号楼的左侧,两楼高度均为90
m,楼间距为AB,冬至日正午,太阳光线与水平面所成的角为32.3°,1号楼在2号楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为55.7°,1号楼在2号楼墙面上的影高为DA.已知CD=42
m.求楼间距AB的长度为多少米?(结果精确到1
m)
解:过点C作CM⊥BE于点M,过点D作DN⊥BE于点N.
则四边形CDNM,ABND是矩形.
∴CD=MN,AB=DN=CM.
在Rt△CEM中,
∵tan∠ECM=,
∴EM=CM·tan32.3°.
在Rt△DEN中,∵tan∠EDN=,
∴EN=DN·tan55.7°.
∵MN=EN-EM,
∴42=AB·tan55.7°-AB·tan32.3°,
解得AB≈50.
答:楼间距AB的长度约为50
m.
