2020-2021学年 北师大版九年级数学下册第一章 1.4解直角三角形 同步练习题(word版含答案)
文档属性
| 名称 | 2020-2021学年 北师大版九年级数学下册第一章 1.4解直角三角形 同步练习题(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 221.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 00:00:00 | ||
图片预览


文档简介
2020-2021学年度北师大版九年级数学下册第一章
1.4解直角三角形
同步练习题
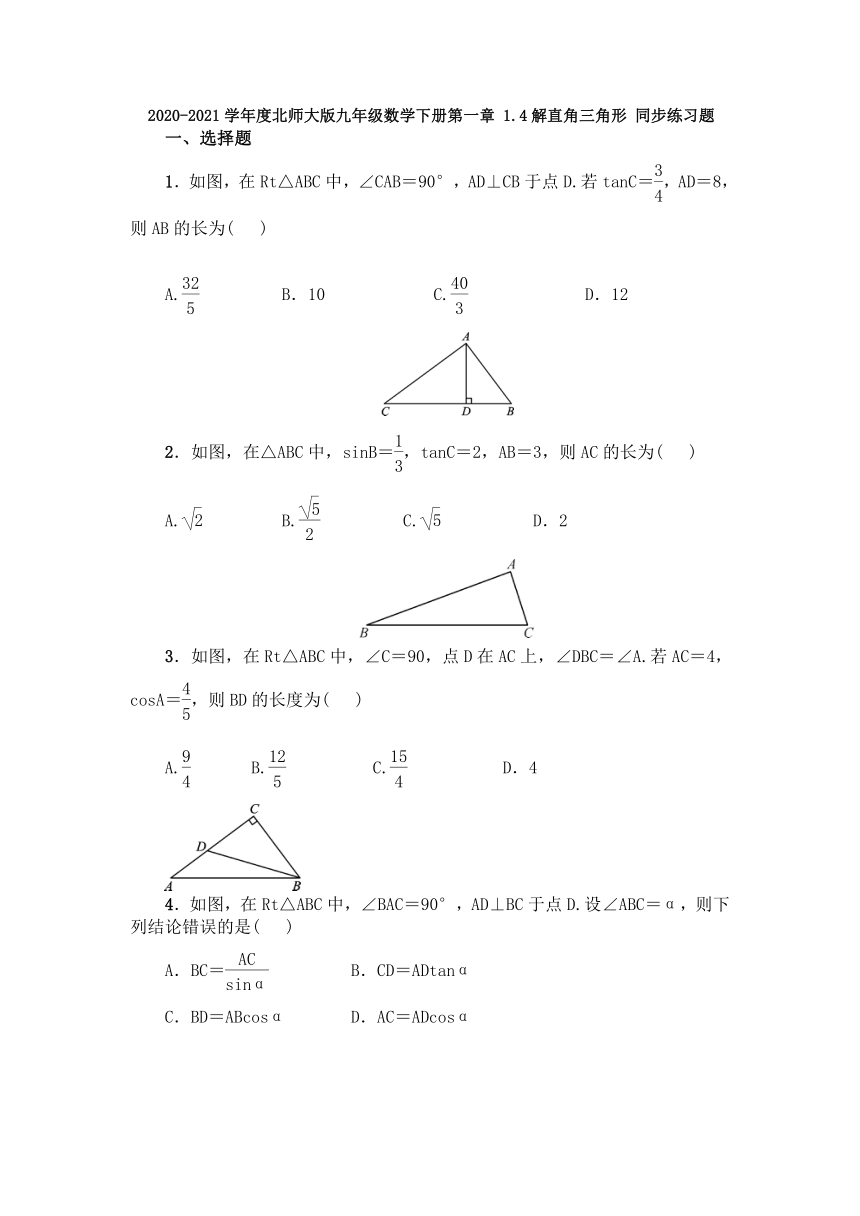
一、选择题
1.如图,在Rt△ABC中,∠CAB=90°,AD⊥CB于点D.若tanC=,AD=8,则AB的长为(
)
A.
B.10
C.
D.12
2.如图,在△ABC中,sinB=,tanC=2,AB=3,则AC的长为(
)
A.
B.
C.
D.2
3.如图,在Rt△ABC中,∠C=90,点D在AC上,∠DBC=∠A.若AC=4,cosA=,则BD的长度为(
)
A.
B.
C.
D.4
4.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D.设∠ABC=α,则下列结论错误的是(
)
A.BC=
B.CD=ADtanα
C.BD=ABcosα
D.AC=ADcosα
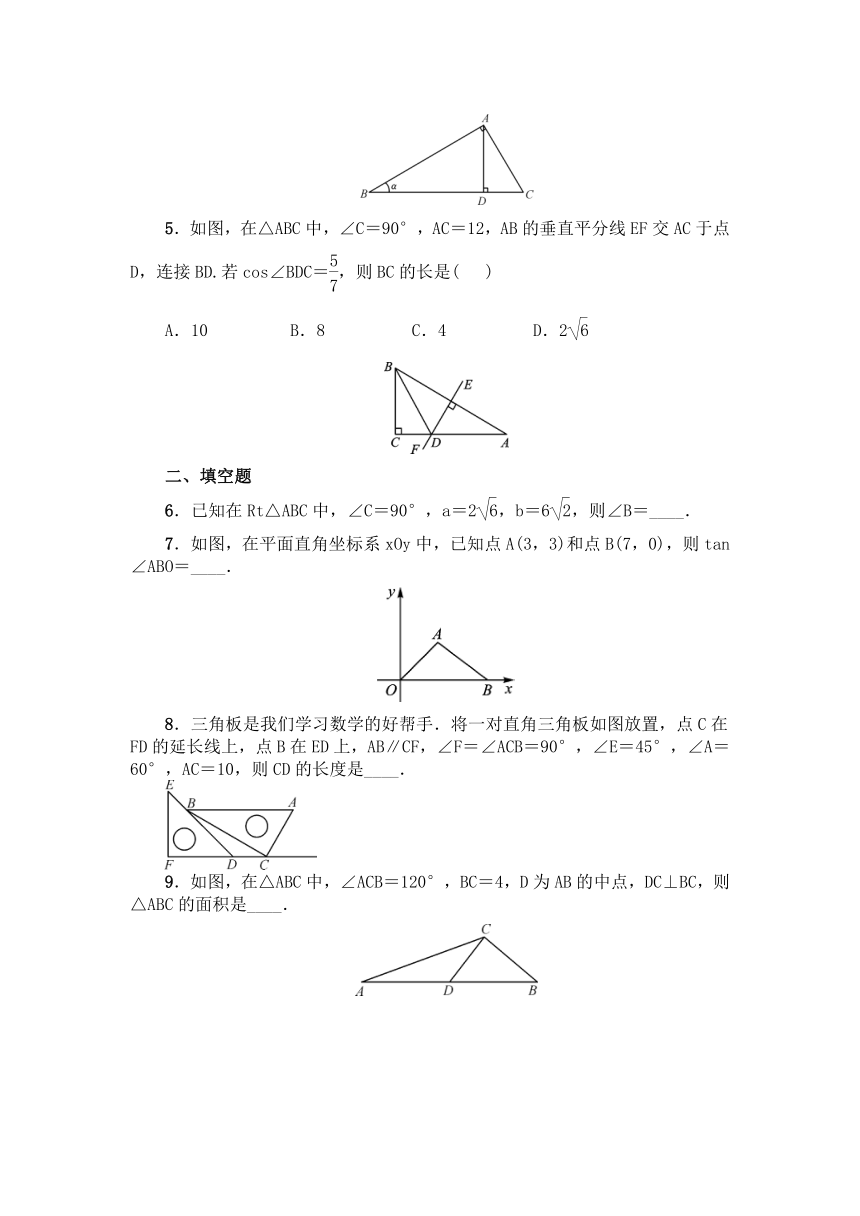
5.如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD.若cos∠BDC=,则BC的长是(
)
A.10
B.8
C.4
D.2
二、填空题
6.已知在Rt△ABC中,∠C=90°,a=2,b=6,则∠B=____.
7.如图,在平面直角坐标系xOy中,已知点A(3,3)和点B(7,0),则tan∠ABO=____.
8.三角板是我们学习数学的好帮手.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是____.
9.如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,DC⊥BC,则△ABC的面积是____.
三、解答题
10.已知在△ABC中,∠A是锐角,AB=c,BC=a,CA=b.
(1)如图1,当∠A=30°,b=6,c=3时,S△ABC=____,bc·sinA=____;
(2)如图2,当∠A=45°,b=6,c=3时,S△ABC=____,bc·sinA=____;
(3)如图3,当∠A=60°,b=4,c=3时,S△ABC=____,bc·sinA=____;
(4)根据(1),(2),(3)题的解答,猜想S△ABC与bc·sinA的大小关系,并给出证明.
11.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.根据下列条件求出直角三角形的其他元素.
(1)已知a=6,b=2;
(2)已知a=24,c=24.
12.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.根据下列条件求出直角三角形的其他元素.
(1)已知∠A=60°,c=4;
(2)已知cosA=,c=20(角度精确到1°).
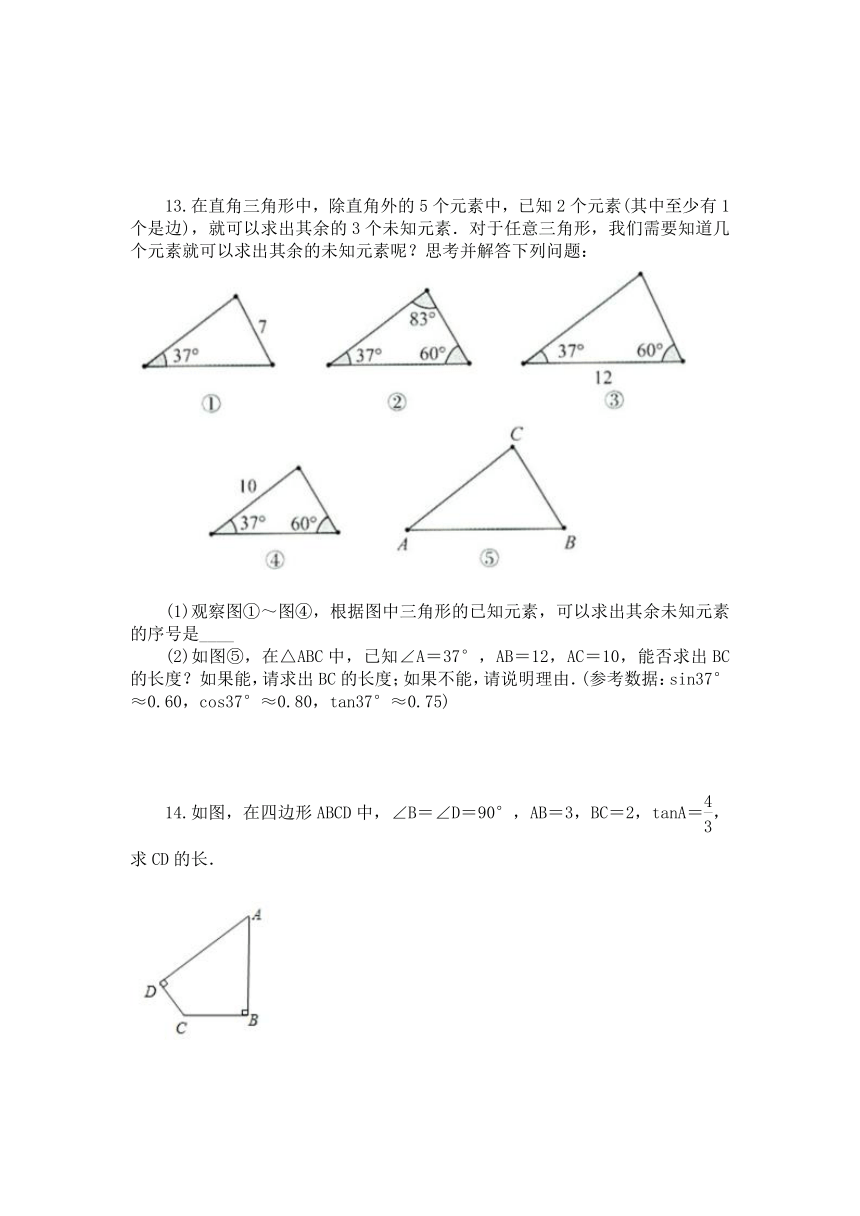
13.在直角三角形中,除直角外的5个元素中,已知2个元素(其中至少有1个是边),就可以求出其余的3个未知元素.对于任意三角形,我们需要知道几个元素就可以求出其余的未知元素呢?思考并解答下列问题:
(1)观察图①~图④,根据图中三角形的已知元素,可以求出其余未知元素的序号是____
(2)如图⑤,在△ABC中,已知∠A=37°,AB=12,AC=10,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
14.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,求CD的长.
参考答案
2020-2021学年度北师大版九年级数学下册第一章
1.4解直角三角形
同步练习题
一、选择题
1.如图,在Rt△ABC中,∠CAB=90°,AD⊥CB于点D.若tanC=,AD=8,则AB的长为(B)
A.
B.10
C.
D.12
2.如图,在△ABC中,sinB=,tanC=2,AB=3,则AC的长为(B)
A.
B.
C.
D.2
3.如图,在Rt△ABC中,∠C=90,点D在AC上,∠DBC=∠A.若AC=4,cosA=,则BD的长度为(C)
A.
B.
C.
D.4
4.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D.设∠ABC=α,则下列结论错误的是(
B
)
A.BC=
B.CD=ADtanα
C.BD=ABcosα
D.AC=ADcosα
5.如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD.若cos∠BDC=,则BC的长是(D)
A.10
B.8
C.4
D.2
二、填空题
6.已知在Rt△ABC中,∠C=90°,a=2,b=6,则∠B=60°.
7.如图,在平面直角坐标系xOy中,已知点A(3,3)和点B(7,0),则tan∠ABO=.
8.三角板是我们学习数学的好帮手.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是15-5.
9.如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,DC⊥BC,则△ABC的面积是8.
三、解答题
10.已知在△ABC中,∠A是锐角,AB=c,BC=a,CA=b.
(1)如图1,当∠A=30°,b=6,c=3时,S△ABC=4.5,bc·sinA=4.5;
(2)如图2,当∠A=45°,b=6,c=3时,S△ABC=,bc·sinA=;
(3)如图3,当∠A=60°,b=4,c=3时,S△ABC=3,bc·sinA=3;
(4)根据(1),(2),(3)题的解答,猜想S△ABC与bc·sinA的大小关系,并给出证明.
解:S△ABC=bc·sinA.证明:
作△ABC的高CD,
在Rt△ABC中,
∵CD=AC·sinA=bsinA,
∴S△ABC=AB·CD=c·bsinA=bc·sinA.
11.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.根据下列条件求出直角三角形的其他元素.
(1)已知a=6,b=2;
(2)已知a=24,c=24.
解:(1)∵在Rt△ABC中,tanA=,
∴tanA==.
∴∠A=60°,∠B=90°-60°=30°.
∴c=2b=2×2=4.
(2)在Rt△ABC中,根据勾股定理有b2=c2-a2,
∵a=24,c=24,
∴b=24.
∴tanA==1.
∴∠A=∠B=45°.
12.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.根据下列条件求出直角三角形的其他元素.
(1)已知∠A=60°,c=4;
(2)已知cosA=,c=20(角度精确到1°).
解:(1)∵在△ABC中,∠C=90°,∠A=60°,
∴∠B=90°-∠A=30°.
∵sinB=,∴b=4×sin30°=2.
∵sinA=,∴a=4×sin60°=6.
(2)∵∠C=90°,cosA=,
∴b=c·cosA=20×=12.
∴a==16.
∵cosA=,∴∠A≈53°.
∴∠B=90°-∠A≈90°-53°=37°.
13.在直角三角形中,除直角外的5个元素中,已知2个元素(其中至少有1个是边),就可以求出其余的3个未知元素.对于任意三角形,我们需要知道几个元素就可以求出其余的未知元素呢?思考并解答下列问题:
(1)观察图①~图④,根据图中三角形的已知元素,可以求出其余未知元素的序号是③④;
(2)如图⑤,在△ABC中,已知∠A=37°,AB=12,AC=10,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
解:过点C作CD⊥AB于点D,
在Rt△ADC中,∠A=37°,
∴CD=AC·sinA=10×sin37°≈10×0.60=6,AD=AC·cosA=10×cos37°≈10×0.80=8.
∴BD=AB-AD≈12-8=4.
∴在Rt△CDB中,
BC=≈=2.
14.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,求CD的长.
解:延长AD和BC交于点E.
∵在Rt△ABE中,tanA==,
∴BE=AB·tanA=4.
∴EC=BE-BC=4-2=2.
∵∠E+∠DCE=90°,∠E+∠A=90°,
∴∠DCE=∠A.
∴在Rt△CDE中,tan∠DCE=tanA==.
∴设DE=4x,则DC=3x.
在Rt△CDE中,EC2=DE2+DC2,
∴4=16x2+9x2,解得x=.
∴CD=.
1.4解直角三角形
同步练习题
一、选择题
1.如图,在Rt△ABC中,∠CAB=90°,AD⊥CB于点D.若tanC=,AD=8,则AB的长为(
)
A.
B.10
C.
D.12
2.如图,在△ABC中,sinB=,tanC=2,AB=3,则AC的长为(
)
A.
B.
C.
D.2
3.如图,在Rt△ABC中,∠C=90,点D在AC上,∠DBC=∠A.若AC=4,cosA=,则BD的长度为(
)
A.
B.
C.
D.4
4.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D.设∠ABC=α,则下列结论错误的是(
)
A.BC=
B.CD=ADtanα
C.BD=ABcosα
D.AC=ADcosα
5.如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD.若cos∠BDC=,则BC的长是(
)
A.10
B.8
C.4
D.2
二、填空题
6.已知在Rt△ABC中,∠C=90°,a=2,b=6,则∠B=____.
7.如图,在平面直角坐标系xOy中,已知点A(3,3)和点B(7,0),则tan∠ABO=____.
8.三角板是我们学习数学的好帮手.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是____.
9.如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,DC⊥BC,则△ABC的面积是____.
三、解答题
10.已知在△ABC中,∠A是锐角,AB=c,BC=a,CA=b.
(1)如图1,当∠A=30°,b=6,c=3时,S△ABC=____,bc·sinA=____;
(2)如图2,当∠A=45°,b=6,c=3时,S△ABC=____,bc·sinA=____;
(3)如图3,当∠A=60°,b=4,c=3时,S△ABC=____,bc·sinA=____;
(4)根据(1),(2),(3)题的解答,猜想S△ABC与bc·sinA的大小关系,并给出证明.
11.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.根据下列条件求出直角三角形的其他元素.
(1)已知a=6,b=2;
(2)已知a=24,c=24.
12.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.根据下列条件求出直角三角形的其他元素.
(1)已知∠A=60°,c=4;
(2)已知cosA=,c=20(角度精确到1°).
13.在直角三角形中,除直角外的5个元素中,已知2个元素(其中至少有1个是边),就可以求出其余的3个未知元素.对于任意三角形,我们需要知道几个元素就可以求出其余的未知元素呢?思考并解答下列问题:
(1)观察图①~图④,根据图中三角形的已知元素,可以求出其余未知元素的序号是____
(2)如图⑤,在△ABC中,已知∠A=37°,AB=12,AC=10,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
14.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,求CD的长.
参考答案
2020-2021学年度北师大版九年级数学下册第一章
1.4解直角三角形
同步练习题
一、选择题
1.如图,在Rt△ABC中,∠CAB=90°,AD⊥CB于点D.若tanC=,AD=8,则AB的长为(B)
A.
B.10
C.
D.12
2.如图,在△ABC中,sinB=,tanC=2,AB=3,则AC的长为(B)
A.
B.
C.
D.2
3.如图,在Rt△ABC中,∠C=90,点D在AC上,∠DBC=∠A.若AC=4,cosA=,则BD的长度为(C)
A.
B.
C.
D.4
4.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D.设∠ABC=α,则下列结论错误的是(
B
)
A.BC=
B.CD=ADtanα
C.BD=ABcosα
D.AC=ADcosα
5.如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD.若cos∠BDC=,则BC的长是(D)
A.10
B.8
C.4
D.2
二、填空题
6.已知在Rt△ABC中,∠C=90°,a=2,b=6,则∠B=60°.
7.如图,在平面直角坐标系xOy中,已知点A(3,3)和点B(7,0),则tan∠ABO=.
8.三角板是我们学习数学的好帮手.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是15-5.
9.如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,DC⊥BC,则△ABC的面积是8.
三、解答题
10.已知在△ABC中,∠A是锐角,AB=c,BC=a,CA=b.
(1)如图1,当∠A=30°,b=6,c=3时,S△ABC=4.5,bc·sinA=4.5;
(2)如图2,当∠A=45°,b=6,c=3时,S△ABC=,bc·sinA=;
(3)如图3,当∠A=60°,b=4,c=3时,S△ABC=3,bc·sinA=3;
(4)根据(1),(2),(3)题的解答,猜想S△ABC与bc·sinA的大小关系,并给出证明.
解:S△ABC=bc·sinA.证明:
作△ABC的高CD,
在Rt△ABC中,
∵CD=AC·sinA=bsinA,
∴S△ABC=AB·CD=c·bsinA=bc·sinA.
11.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.根据下列条件求出直角三角形的其他元素.
(1)已知a=6,b=2;
(2)已知a=24,c=24.
解:(1)∵在Rt△ABC中,tanA=,
∴tanA==.
∴∠A=60°,∠B=90°-60°=30°.
∴c=2b=2×2=4.
(2)在Rt△ABC中,根据勾股定理有b2=c2-a2,
∵a=24,c=24,
∴b=24.
∴tanA==1.
∴∠A=∠B=45°.
12.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.根据下列条件求出直角三角形的其他元素.
(1)已知∠A=60°,c=4;
(2)已知cosA=,c=20(角度精确到1°).
解:(1)∵在△ABC中,∠C=90°,∠A=60°,
∴∠B=90°-∠A=30°.
∵sinB=,∴b=4×sin30°=2.
∵sinA=,∴a=4×sin60°=6.
(2)∵∠C=90°,cosA=,
∴b=c·cosA=20×=12.
∴a==16.
∵cosA=,∴∠A≈53°.
∴∠B=90°-∠A≈90°-53°=37°.
13.在直角三角形中,除直角外的5个元素中,已知2个元素(其中至少有1个是边),就可以求出其余的3个未知元素.对于任意三角形,我们需要知道几个元素就可以求出其余的未知元素呢?思考并解答下列问题:
(1)观察图①~图④,根据图中三角形的已知元素,可以求出其余未知元素的序号是③④;
(2)如图⑤,在△ABC中,已知∠A=37°,AB=12,AC=10,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
解:过点C作CD⊥AB于点D,
在Rt△ADC中,∠A=37°,
∴CD=AC·sinA=10×sin37°≈10×0.60=6,AD=AC·cosA=10×cos37°≈10×0.80=8.
∴BD=AB-AD≈12-8=4.
∴在Rt△CDB中,
BC=≈=2.
14.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,求CD的长.
解:延长AD和BC交于点E.
∵在Rt△ABE中,tanA==,
∴BE=AB·tanA=4.
∴EC=BE-BC=4-2=2.
∵∠E+∠DCE=90°,∠E+∠A=90°,
∴∠DCE=∠A.
∴在Rt△CDE中,tan∠DCE=tanA==.
∴设DE=4x,则DC=3x.
在Rt△CDE中,EC2=DE2+DC2,
∴4=16x2+9x2,解得x=.
∴CD=.
