2020-2021学年 北师大版九年级数学下册第一章 1.1.1 正切 同步练习题(word版含答案)
文档属性
| 名称 | 2020-2021学年 北师大版九年级数学下册第一章 1.1.1 正切 同步练习题(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 120.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 06:40:09 | ||
图片预览




文档简介
2020-2021学年度北师大版九年级数学下册第一章
1.1.1
正切
同步练习题
一、选择题
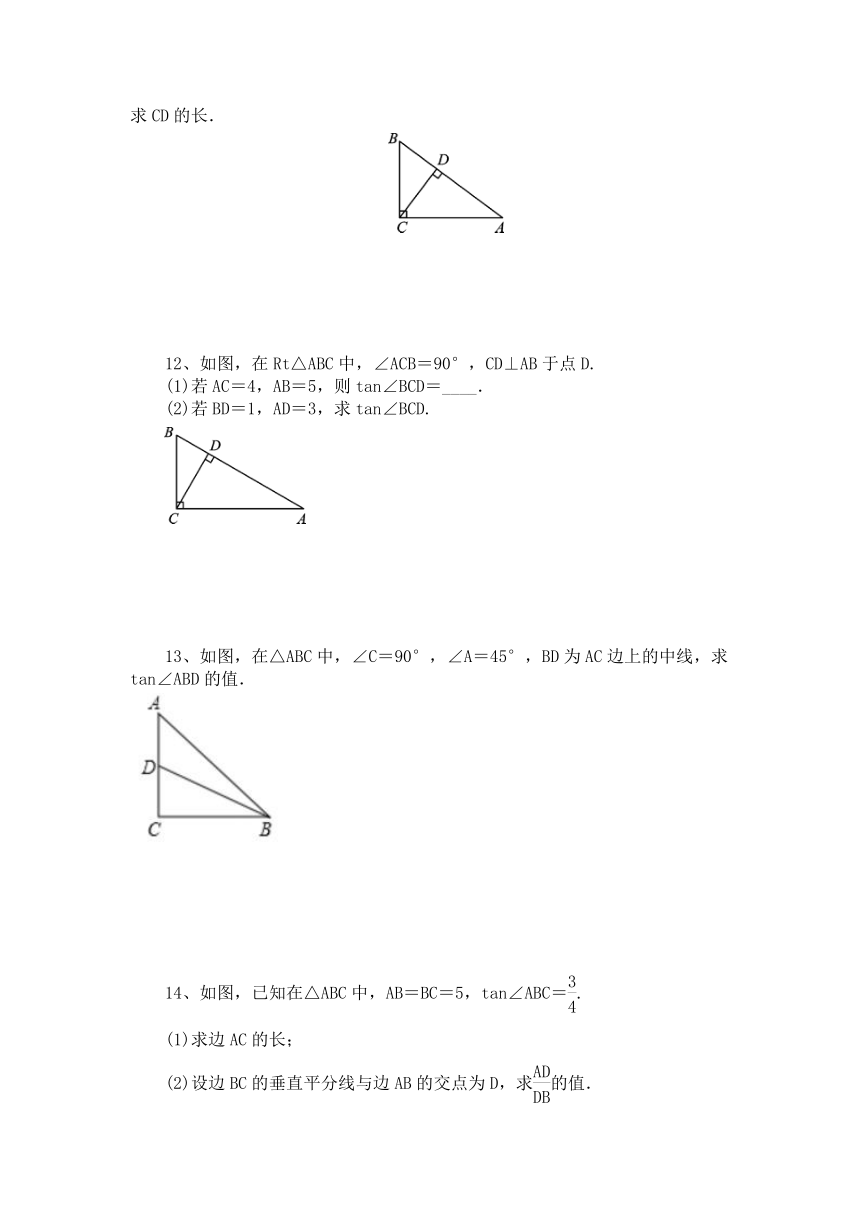
1、如图,在△ABC中,∠ACB=90°,AB=5,AC=3,则tanB的值为(
)
A.
B.
C.
D.
2、如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为(
)
A.
B.
C.
D.
3、如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知AB=6,AC=3,则tan∠BCD的值为(
)
A.
B.
C.
D.
4、如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为(
)
A.
B.
C.2
D.2
二、填空题
5、在Rt△ABC中,∠C=90°,若AC=3,BC=2,则tanA=____.
6、在△ABC中,∠C=90°,BC=6
cm,tanA=,则AC的长为9cm,AB的长为____.
7、如图所示,河堤横断面迎水坡AB的坡比是1∶,堤高BC=4
m,则迎水坡宽度AC的长为____.
8、如图,斜坡AC的坡度是i=1∶3(坡角的正切叫坡度),AB=2
m,一汽车从坡底C处行驶到坡顶A处,则它行驶过的坡面距离AC的长为____.
9、如图,在Rt△ABC中,∠C=90°,tanB=,AB=10,则AC=____.
10、如图,点P(12,a)在反比例函数y=的图象上,PH⊥x轴于点H,则tan∠POH的值为____.
三、解答题
11、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,tanA=,AB=25,求CD的长.
12、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
(1)若AC=4,AB=5,则tan∠BCD=____.
(2)若BD=1,AD=3,求tan∠BCD.
13、如图,在△ABC中,∠C=90°,∠A=45°,BD为AC边上的中线,求tan∠ABD的值.
14、如图,已知在△ABC中,AB=BC=5,tan∠ABC=.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
15、某学校为增加体育馆观众座席数量,决定对体育馆进行施工改造.如图为体育馆改造的截面示意图.已知原座位区最高点A到地面的铅直高度AC长度为15米,原坡面AB的倾斜角∠ABC为45°,原坡脚B与场馆中央的运动区边界的安全距离BD为5米.如果按照施工方提供的设计方案施工,新座位区最高点E到地面的铅直高度EG长度保持15米不变,使A,E两点间距离为2米,使改造后坡面EF的倾斜角∠EFG为37°.若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米(即FD≥2.5),请问施工方提供的设计方案是否满足安全要求呢?请说明理由.(参考数据:tan37°≈)
参考答案
2020-2021学年度北师大版九年级数学下册第一章
1.1.1
正切
同步练习题
一、选择题
1、如图,在△ABC中,∠ACB=90°,AB=5,AC=3,则tanB的值为(D)
A.
B.
C.
D.
2、如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为(D)
A.
B.
C.
D.
3、如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知AB=6,AC=3,则tan∠BCD的值为(A)
A.
B.
C.
D.
4、如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为(A)
A.
B.
C.2
D.2
二、填空题
5、在Rt△ABC中,∠C=90°,若AC=3,BC=2,则tanA=.
6、在△ABC中,∠C=90°,BC=6
cm,tanA=,则AC的长为9cm,AB的长为3cm.
7、如图所示,河堤横断面迎水坡AB的坡比是1∶,堤高BC=4
m,则迎水坡宽度AC的长为4m.
8、如图,斜坡AC的坡度是i=1∶3(坡角的正切叫坡度),AB=2
m,一汽车从坡底C处行驶到坡顶A处,则它行驶过的坡面距离AC的长为2m.
9、如图,在Rt△ABC中,∠C=90°,tanB=,AB=10,则AC=2.
10、如图,点P(12,a)在反比例函数y=的图象上,PH⊥x轴于点H,则tan∠POH的值为.
三、解答题
11、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,tanA=,AB=25,求CD的长.
解:∵tanA==,
∴设BC=3x,AC=4x.
在Rt△ABC中,BC2+AC2=AB2.
∴(3x)2+(4x)2=252,解得x=5.
∴BC=15,AC=20.
∵S△ABC=AB·CD=BC·AC,
∴×25×CD=×15×20,解得CD=12.
12、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
(1)若AC=4,AB=5,则tan∠BCD=;
(2)若BD=1,AD=3,求tan∠BCD.
解:∵∠ACB=90°,CD⊥AB,
∴∠A+∠DCA=90°,∠DCA+∠BCD=90°,∠BDC=∠CDA=90°.
∴∠A=∠BCD.
∴△BCD∽△CAD.∴=.
∴CD2=BD·AD=3,解得CD=.
∴tan∠BCD==.
13、如图,在△ABC中,∠C=90°,∠A=45°,BD为AC边上的中线,求tan∠ABD的值.
解:过点D作DE⊥AB于点E,
∵∠C=90°,∠A=45°,
∴∠ABC=45°.∴AC=BC.
设BC=2a,则AC=2a,AD=CD=a.
在Rt△ACB中,AB==2a.
∵∠A=45°,∠DEA=90°,∴∠ADE=45°.
∴AE=DE=a.
∴BE=AB-AE=a.
∴tan∠ABD===.
14、如图,已知在△ABC中,AB=BC=5,tan∠ABC=.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
解:(1)过点A作AE⊥BC于点E,
在Rt△ABE中,AE2+BE2=AB2,tan∠ABC==.
设AE=3x,BE=4x.
∵AB=5,∴(3x)2+(4x)2=52,解得x=1.
∴AE=3,BE=4.
∴CE=BC-BE=5-4=1.
在Rt△AEC中,AC==.
(2)过点D作DF⊥BC于点F,连接CD,则
DF垂直平分BC,∴BD=CD,BF=CF=.
∵tan∠DBF==,∴DF=.
在Rt△BFD中,BD==.
∴AD=5-=.∴=.
15、某学校为增加体育馆观众座席数量,决定对体育馆进行施工改造.如图为体育馆改造的截面示意图.已知原座位区最高点A到地面的铅直高度AC长度为15米,原坡面AB的倾斜角∠ABC为45°,原坡脚B与场馆中央的运动区边界的安全距离BD为5米.如果按照施工方提供的设计方案施工,新座位区最高点E到地面的铅直高度EG长度保持15米不变,使A,E两点间距离为2米,使改造后坡面EF的倾斜角∠EFG为37°.若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米(即FD≥2.5),请问施工方提供的设计方案是否满足安全要求呢?请说明理由.(参考数据:tan37°≈)
解:施工方提供的设计方案不满足安全要求.理由如下:
在Rt△ABC中,∠ABC=45°,
∴∠CAB=45°.∴BC=AC=15米.
在Rt△EFG中,EG=15米,∠EFG=37°,
∴GF=≈=20(米).
依题意,得四边形EGCA是矩形.
∴GC=EA=2米.
∴BF=GF-GC-BC≈20-2-15=3(米).
∵BD=5米,∴FD=BD-BF≈5-3=2<2.5.
∴施工方提供的设计方案不满足安全要求.
1.1.1
正切
同步练习题
一、选择题
1、如图,在△ABC中,∠ACB=90°,AB=5,AC=3,则tanB的值为(
)
A.
B.
C.
D.
2、如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为(
)
A.
B.
C.
D.
3、如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知AB=6,AC=3,则tan∠BCD的值为(
)
A.
B.
C.
D.
4、如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为(
)
A.
B.
C.2
D.2
二、填空题
5、在Rt△ABC中,∠C=90°,若AC=3,BC=2,则tanA=____.
6、在△ABC中,∠C=90°,BC=6
cm,tanA=,则AC的长为9cm,AB的长为____.
7、如图所示,河堤横断面迎水坡AB的坡比是1∶,堤高BC=4
m,则迎水坡宽度AC的长为____.
8、如图,斜坡AC的坡度是i=1∶3(坡角的正切叫坡度),AB=2
m,一汽车从坡底C处行驶到坡顶A处,则它行驶过的坡面距离AC的长为____.
9、如图,在Rt△ABC中,∠C=90°,tanB=,AB=10,则AC=____.
10、如图,点P(12,a)在反比例函数y=的图象上,PH⊥x轴于点H,则tan∠POH的值为____.
三、解答题
11、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,tanA=,AB=25,求CD的长.
12、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
(1)若AC=4,AB=5,则tan∠BCD=____.
(2)若BD=1,AD=3,求tan∠BCD.
13、如图,在△ABC中,∠C=90°,∠A=45°,BD为AC边上的中线,求tan∠ABD的值.
14、如图,已知在△ABC中,AB=BC=5,tan∠ABC=.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
15、某学校为增加体育馆观众座席数量,决定对体育馆进行施工改造.如图为体育馆改造的截面示意图.已知原座位区最高点A到地面的铅直高度AC长度为15米,原坡面AB的倾斜角∠ABC为45°,原坡脚B与场馆中央的运动区边界的安全距离BD为5米.如果按照施工方提供的设计方案施工,新座位区最高点E到地面的铅直高度EG长度保持15米不变,使A,E两点间距离为2米,使改造后坡面EF的倾斜角∠EFG为37°.若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米(即FD≥2.5),请问施工方提供的设计方案是否满足安全要求呢?请说明理由.(参考数据:tan37°≈)
参考答案
2020-2021学年度北师大版九年级数学下册第一章
1.1.1
正切
同步练习题
一、选择题
1、如图,在△ABC中,∠ACB=90°,AB=5,AC=3,则tanB的值为(D)
A.
B.
C.
D.
2、如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为(D)
A.
B.
C.
D.
3、如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,已知AB=6,AC=3,则tan∠BCD的值为(A)
A.
B.
C.
D.
4、如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为(A)
A.
B.
C.2
D.2
二、填空题
5、在Rt△ABC中,∠C=90°,若AC=3,BC=2,则tanA=.
6、在△ABC中,∠C=90°,BC=6
cm,tanA=,则AC的长为9cm,AB的长为3cm.
7、如图所示,河堤横断面迎水坡AB的坡比是1∶,堤高BC=4
m,则迎水坡宽度AC的长为4m.
8、如图,斜坡AC的坡度是i=1∶3(坡角的正切叫坡度),AB=2
m,一汽车从坡底C处行驶到坡顶A处,则它行驶过的坡面距离AC的长为2m.
9、如图,在Rt△ABC中,∠C=90°,tanB=,AB=10,则AC=2.
10、如图,点P(12,a)在反比例函数y=的图象上,PH⊥x轴于点H,则tan∠POH的值为.
三、解答题
11、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,tanA=,AB=25,求CD的长.
解:∵tanA==,
∴设BC=3x,AC=4x.
在Rt△ABC中,BC2+AC2=AB2.
∴(3x)2+(4x)2=252,解得x=5.
∴BC=15,AC=20.
∵S△ABC=AB·CD=BC·AC,
∴×25×CD=×15×20,解得CD=12.
12、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
(1)若AC=4,AB=5,则tan∠BCD=;
(2)若BD=1,AD=3,求tan∠BCD.
解:∵∠ACB=90°,CD⊥AB,
∴∠A+∠DCA=90°,∠DCA+∠BCD=90°,∠BDC=∠CDA=90°.
∴∠A=∠BCD.
∴△BCD∽△CAD.∴=.
∴CD2=BD·AD=3,解得CD=.
∴tan∠BCD==.
13、如图,在△ABC中,∠C=90°,∠A=45°,BD为AC边上的中线,求tan∠ABD的值.
解:过点D作DE⊥AB于点E,
∵∠C=90°,∠A=45°,
∴∠ABC=45°.∴AC=BC.
设BC=2a,则AC=2a,AD=CD=a.
在Rt△ACB中,AB==2a.
∵∠A=45°,∠DEA=90°,∴∠ADE=45°.
∴AE=DE=a.
∴BE=AB-AE=a.
∴tan∠ABD===.
14、如图,已知在△ABC中,AB=BC=5,tan∠ABC=.
(1)求边AC的长;
(2)设边BC的垂直平分线与边AB的交点为D,求的值.
解:(1)过点A作AE⊥BC于点E,
在Rt△ABE中,AE2+BE2=AB2,tan∠ABC==.
设AE=3x,BE=4x.
∵AB=5,∴(3x)2+(4x)2=52,解得x=1.
∴AE=3,BE=4.
∴CE=BC-BE=5-4=1.
在Rt△AEC中,AC==.
(2)过点D作DF⊥BC于点F,连接CD,则
DF垂直平分BC,∴BD=CD,BF=CF=.
∵tan∠DBF==,∴DF=.
在Rt△BFD中,BD==.
∴AD=5-=.∴=.
15、某学校为增加体育馆观众座席数量,决定对体育馆进行施工改造.如图为体育馆改造的截面示意图.已知原座位区最高点A到地面的铅直高度AC长度为15米,原坡面AB的倾斜角∠ABC为45°,原坡脚B与场馆中央的运动区边界的安全距离BD为5米.如果按照施工方提供的设计方案施工,新座位区最高点E到地面的铅直高度EG长度保持15米不变,使A,E两点间距离为2米,使改造后坡面EF的倾斜角∠EFG为37°.若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米(即FD≥2.5),请问施工方提供的设计方案是否满足安全要求呢?请说明理由.(参考数据:tan37°≈)
解:施工方提供的设计方案不满足安全要求.理由如下:
在Rt△ABC中,∠ABC=45°,
∴∠CAB=45°.∴BC=AC=15米.
在Rt△EFG中,EG=15米,∠EFG=37°,
∴GF=≈=20(米).
依题意,得四边形EGCA是矩形.
∴GC=EA=2米.
∴BF=GF-GC-BC≈20-2-15=3(米).
∵BD=5米,∴FD=BD-BF≈5-3=2<2.5.
∴施工方提供的设计方案不满足安全要求.
