2020-2021学年七年级下册数学鲁教五四新版《第8章 平行线的有关证明》单元测试题(word版有答案)
文档属性
| 名称 | 2020-2021学年七年级下册数学鲁教五四新版《第8章 平行线的有关证明》单元测试题(word版有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 110.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 00:00:00 | ||
图片预览



文档简介
2020-2021学年七年级下册数学鲁教五四新版《第8章
平行线的有关证明》单元测试题
一.选择题
1.下列说法不正确的是( )
A.若两相等的角有一边平行,则另一边也互相平行
B.两条直线相交,所成的两组对顶角的平分线互相垂直
C.两条平行线被第三条直线所截,同旁内角的平分线互相垂直
D.在同一个平面内,经过直线外一点,有且只有一条直线与这条直线垂直
2.在A,B,C三个盒子中分别装有红、黄、蓝颜色的小球中的一种,将它们分别给甲、乙、丙三个人.已知甲没有得到A盒;乙没有得到B盒,也没有得到黄球;A盒中没有装红球,B盒中装着蓝球.则丙得到的盒子编号和小球的颜色分别是( )
A.A,黄
B.B,蓝
C.C,红
D.C,黄
3.下列说法正确的是( )
A.过一点能作已知直线的一条平行线
B.过一点能作已知直线的一条垂线
C.射线AB的端点是A和B
D.点可以用一个大写字母表示,也可用小写字母表示
4.下列命题中,不正确的为( )
A.钝角三角形是斜三角形
B.在一个三角形中至多有一个内角不小于60o
C.三角形的没有公共顶点的两个外角的和大于平角
D.三角形的外角中,最小的一个是钝角,那它一定是锐角三角形
5.如图,下列条件中,不能判断AB∥CD的是( )
A.∠3=∠2
B.∠1=∠4
C.∠B=∠5
D.∠D+∠BAD=180°
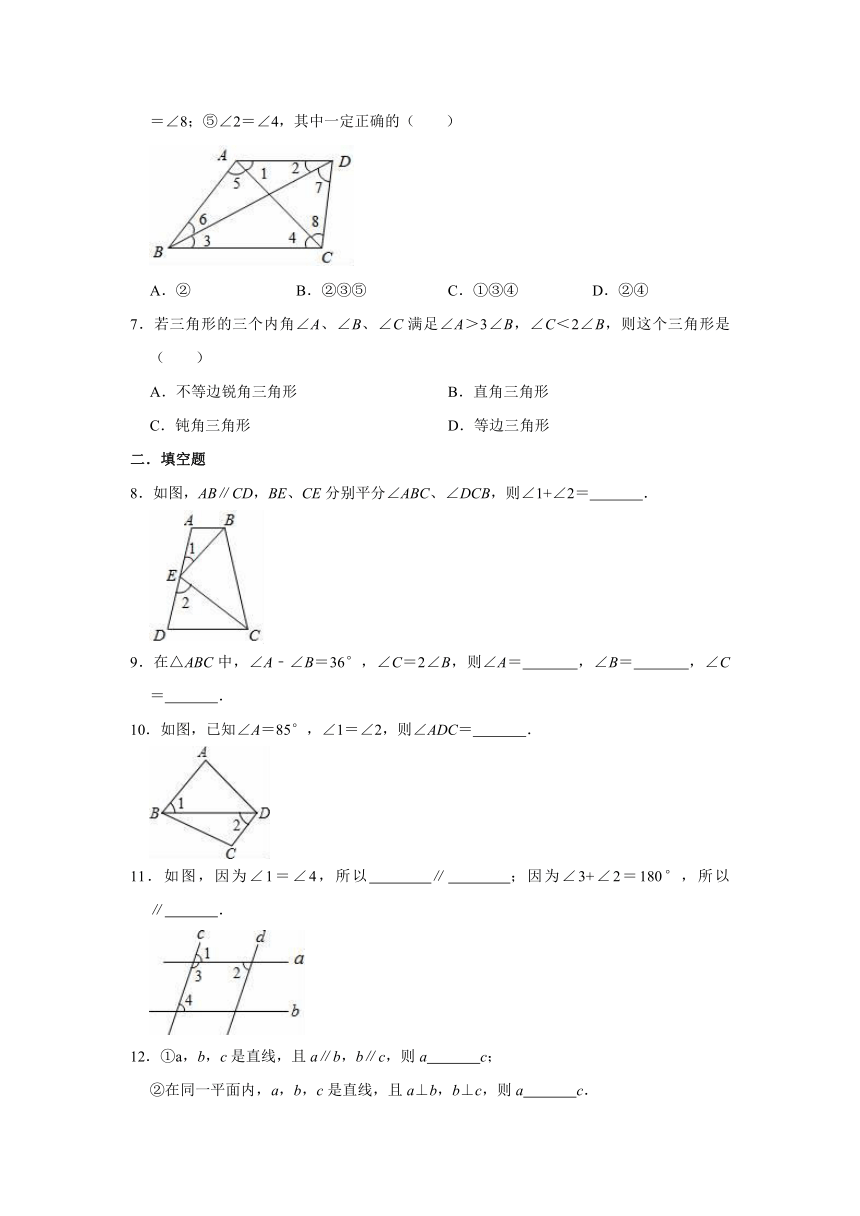
6.如图所示,已知AD∥BC,则下列结论:①∠1=∠2;②∠2=∠3;③∠6=∠8;④∠5=∠8;⑤∠2=∠4,其中一定正确的( )
A.②
B.②③⑤
C.①③④
D.②④
7.若三角形的三个内角∠A、∠B、∠C满足∠A>3∠B,∠C<2∠B,则这个三角形是( )
A.不等边锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
二.填空题
8.如图,AB∥CD,BE、CE分别平分∠ABC、∠DCB,则∠1+∠2=
.
9.在△ABC中,∠A﹣∠B=36°,∠C=2∠B,则∠A=
,∠B=
,∠C=
.
10.如图,已知∠A=85°,∠1=∠2,则∠ADC=
.
11.如图,因为∠1=∠4,所以
∥
;因为∠3+∠2=180°,所以
∥
.
12.①a,b,c是直线,且a∥b,b∥c,则a
c;
②在同一平面内,a,b,c是直线,且a⊥b,b⊥c,则a
c.
13.四个空矿泉水瓶可以换一瓶矿泉水,现拿16个空矿泉水瓶,最多能喝
瓶矿泉水.
14.根据命题结论正确与否,命题可分为
和
.
三.解答题
15.直线AB、CD与GH交于E、F,EM平分∠BEF,FN平分∠DFH,∠BEF=∠DFH,
求证:EM∥FN.
16.写出下列各命题的逆命题,并判断其逆命题是真命题还是假命题,请举出一个反例说明.
(1)两直线平行,同旁内角互补.
(2)垂直于同一条直线的两直线平行.
(3)相等的角是内错角.
(4)等底等高的三角形面积相等.
17.老师与学生小王、小张、小李玩帽子游戏,老师先给三位学生看了四顶帽子,其中二顶是红色的,一顶蓝色的,还有一顶是黄色的.然后让他们先闭上眼睛,给他们每人戴上一顶帽子后,睁开眼睛看其他学生帽子的颜色,然后说出自己所戴帽子的颜色,小李看到的颜色是:小王的帽子是红色的,小张的帽子是黄色的,同时看到小王,小张无法马上说出自己帽子的颜色,这时小李立刻猜出自己所戴帽子的颜色,小李帽子的颜色是什么?为什么?
18.如图所示,已知AB∥CD∥EF,BC∥AD,AC平分∠BAD,在图中找出和∠AGE相等的角,并说明理由.
19.如图,AD、AE分别为△ABC的高和角平分线,∠B=35°,∠C=45°,求∠DAE的度数.
20.如图,△ABC中,D,E,F分别为三边BC,BA,AC上的点,∠B=∠DEB,∠C=∠DFC.若∠A=70°,求∠EDF的度数.
参考答案与试题解析
一.选择题
1.解:A、若两相等的角有一边平行,则另一边也互相平行或者相交,所以说法错误;
B、两条直线相交,所成的两组对顶角的平分线互相垂直,说法正确;
C、两条平行线被第三条直线所截,同旁内角的平分线互相垂直,说法正确;
D、在同一个平面内,经过直线外一点,有且只有一条直线与这条直线垂直,说法正确;
故选:A.
2.解:已知A盒中没有装红球,而B盒中装着蓝球,则A盒装的是黄球,C盒装的是红球;
由于乙没有得到B盒,也没有得到黄球,因此乙得到的是C盒;
由于甲没有得到A盒,因此丙得到的是A盒,装的是黄球.故选A.
3.解:A、过已知直线外一点能作已知直线的一条平行线,故本选项错误;
B、过一点能作已知直线的一条垂线,正确;
C、射线AB的端点是A,故本选项错误;
D、点可以用一个大写字母表示,不可用小写字母表示,故本选项错误.
故选:B.
4.解:A、钝角三角形是斜三角形,正确,不符合题意;
B、在一个三角形中至少有一个内角不小于60°,错误,不符合题意;
C、三角形的没有公共顶点的两个外角的和大于平角,正确,符合题意;
D、三角形的外角中,最小的一个是钝角,那它一定是锐角三角形,正确,不符合题意,
故选:B.
5.解:A、∠3和∠2是直线AB、CD被直线AC所截形成的内错角,内错角相等,可以判断AB∥CD,不符合题意;
B、∠1和∠4是直线AD、BC被直线AC所截形成的内错角,内错角相等,可以判断AD∥BC,不能判断AB∥CD,符合题意;
C、∠B和∠5是直线直线AB、CD被直线BE所截形成的同位角,同位角相等,可以判断AB∥CD,不符合题意;
D、∠D和∠BAD直线直线AB、CD被直线AD所截形成的同旁内角,同旁内角互补,可以判断AB∥CD,不符合题意;
故选:B.
6.解:∵AD∥BC,
∴∠2=∠3,
故选:A.
7.解:根据题意∠A>3∠B,即有∠B<∠A,
又∠C<2∠B<∠A,
所以∠A+∠B+∠C<∠A+∠A+∠A=2∠A,
故有180°<2∠A,
得∠A>90°,
即得△ABC为钝角三角形.
故选:C.
二.填空题
8.解:∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵BE是∠ABC的平分线,
∴∠EBC=∠ABC,
又∵CE是∠BCD的平分线,
∴∠ECB=∠DCB,
∴∠EBC+∠ECB=(∠ABC+∠BCD)=90°,
∴∠BEC=180°﹣(∠EBC+∠ECB)=90°,
∴∠1+∠2=90°.
故答案为:90°.
9.解:由题意得,
解得,
故答案为72°,36°,72°.
10.解:∵∠1=∠2,
∴AB∥CD,
∴∠A+∠ADC=180°,
∵∠A=85°,
∴∠ADC=95°.
故答案为:95°.
11.解:∵∠1=∠4
∴a∥b;
∵∠3+∠2=180°,
∴c∥d.
故答案为:a;b;c;d
12.解:①∵a∥b,b∥c,∴a∥c(平行于同一条直线的两直线平行);
②在同一平面内,∵a⊥b,b⊥c,∴a∥c(垂直于同一条直线的两直线平行).
13.解:16个空瓶可换16÷4=4瓶矿泉水;
4瓶矿泉水喝完后又可得到4个空瓶子,
可换4÷4=1瓶矿泉水;
因此最多可以喝矿泉水4+1=5瓶.
故答案为:5.
14.解:根据命题结论正确与否,命题可分为:真命题和假命题.
三.解答题
15.证明:∵EM平分∠BEF,FN平分∠DFH,
∴∠BEF=2∠MEF,∠DFH=2∠NFH,
∵∠BEF=∠DFH,
∴∠MEF=∠NFH,
∴EM∥FN.
16.解:(1)同旁内角互补,两直线平行,真命题;
(2)如果两条直线平行,那么这两条直线垂直于同一条直线(在同一平面内),真命题;
(3)内错角相等,假命题;例如:∠1与∠2是内错角,但不相等;
(4)面积相等的三角形等底等高,是假命题.例如:底边是2,高是4的三角形与底边是4,高是2的三角形.
17.解:红色.理由如下:小李看到小王、小张戴红色和黄色帽子,则小李可能戴蓝色或红色帽子,若小李戴蓝色帽子,则小王必能说出自己帽子颜色为红色,但小王、小张都无法马上说出自己帽子颜色,所以小李的帽子颜色为红色.
18.解:∠AGE=∠CGF,对顶角相等;
∠AGE=∠ACD,两直线平行,同位角相等;
∠AGE=∠CAB,两直线平行,内错角相等;
∵∠DAC=∠CAB,
∴∠DAC=∠AGE;
∵BC∥AD,
∴∠DAC=∠ACB,
又∵∠DAC=∠AGE,
∴∠AGE=∠ACB;
综上所述,和∠AGE相等的角有:∠CGF,∠ACD,∠CAB,∠DAC,∠ACB.
19.解:在△ABC中,∵AE平分∠BAC,
∴∠CAE=∠BAC,
∵∠B=35°,∠C=45°,
∴∠BAC=100°,∠DAC=45°,
∴∠CAE=50°,
∴∠DAE=∠CAE﹣∠DAC=5°.
20.解:∵∠A+∠B+∠C=180°,
∴∠B+∠C=110°,
∵∠B=∠DEB,∠C=∠DFC,
∴∠B+∠DEB+∠C+∠DFC=220°,
∵∠B+∠DEB+∠C+∠DFC+∠EDB+∠FDC=360°,
∴∠EDB+∠FDC=140°,
即∠EDF=180°﹣140°=40°
平行线的有关证明》单元测试题
一.选择题
1.下列说法不正确的是( )
A.若两相等的角有一边平行,则另一边也互相平行
B.两条直线相交,所成的两组对顶角的平分线互相垂直
C.两条平行线被第三条直线所截,同旁内角的平分线互相垂直
D.在同一个平面内,经过直线外一点,有且只有一条直线与这条直线垂直
2.在A,B,C三个盒子中分别装有红、黄、蓝颜色的小球中的一种,将它们分别给甲、乙、丙三个人.已知甲没有得到A盒;乙没有得到B盒,也没有得到黄球;A盒中没有装红球,B盒中装着蓝球.则丙得到的盒子编号和小球的颜色分别是( )
A.A,黄
B.B,蓝
C.C,红
D.C,黄
3.下列说法正确的是( )
A.过一点能作已知直线的一条平行线
B.过一点能作已知直线的一条垂线
C.射线AB的端点是A和B
D.点可以用一个大写字母表示,也可用小写字母表示
4.下列命题中,不正确的为( )
A.钝角三角形是斜三角形
B.在一个三角形中至多有一个内角不小于60o
C.三角形的没有公共顶点的两个外角的和大于平角
D.三角形的外角中,最小的一个是钝角,那它一定是锐角三角形
5.如图,下列条件中,不能判断AB∥CD的是( )
A.∠3=∠2
B.∠1=∠4
C.∠B=∠5
D.∠D+∠BAD=180°
6.如图所示,已知AD∥BC,则下列结论:①∠1=∠2;②∠2=∠3;③∠6=∠8;④∠5=∠8;⑤∠2=∠4,其中一定正确的( )
A.②
B.②③⑤
C.①③④
D.②④
7.若三角形的三个内角∠A、∠B、∠C满足∠A>3∠B,∠C<2∠B,则这个三角形是( )
A.不等边锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
二.填空题
8.如图,AB∥CD,BE、CE分别平分∠ABC、∠DCB,则∠1+∠2=
.
9.在△ABC中,∠A﹣∠B=36°,∠C=2∠B,则∠A=
,∠B=
,∠C=
.
10.如图,已知∠A=85°,∠1=∠2,则∠ADC=
.
11.如图,因为∠1=∠4,所以
∥
;因为∠3+∠2=180°,所以
∥
.
12.①a,b,c是直线,且a∥b,b∥c,则a
c;
②在同一平面内,a,b,c是直线,且a⊥b,b⊥c,则a
c.
13.四个空矿泉水瓶可以换一瓶矿泉水,现拿16个空矿泉水瓶,最多能喝
瓶矿泉水.
14.根据命题结论正确与否,命题可分为
和
.
三.解答题
15.直线AB、CD与GH交于E、F,EM平分∠BEF,FN平分∠DFH,∠BEF=∠DFH,
求证:EM∥FN.
16.写出下列各命题的逆命题,并判断其逆命题是真命题还是假命题,请举出一个反例说明.
(1)两直线平行,同旁内角互补.
(2)垂直于同一条直线的两直线平行.
(3)相等的角是内错角.
(4)等底等高的三角形面积相等.
17.老师与学生小王、小张、小李玩帽子游戏,老师先给三位学生看了四顶帽子,其中二顶是红色的,一顶蓝色的,还有一顶是黄色的.然后让他们先闭上眼睛,给他们每人戴上一顶帽子后,睁开眼睛看其他学生帽子的颜色,然后说出自己所戴帽子的颜色,小李看到的颜色是:小王的帽子是红色的,小张的帽子是黄色的,同时看到小王,小张无法马上说出自己帽子的颜色,这时小李立刻猜出自己所戴帽子的颜色,小李帽子的颜色是什么?为什么?
18.如图所示,已知AB∥CD∥EF,BC∥AD,AC平分∠BAD,在图中找出和∠AGE相等的角,并说明理由.
19.如图,AD、AE分别为△ABC的高和角平分线,∠B=35°,∠C=45°,求∠DAE的度数.
20.如图,△ABC中,D,E,F分别为三边BC,BA,AC上的点,∠B=∠DEB,∠C=∠DFC.若∠A=70°,求∠EDF的度数.
参考答案与试题解析
一.选择题
1.解:A、若两相等的角有一边平行,则另一边也互相平行或者相交,所以说法错误;
B、两条直线相交,所成的两组对顶角的平分线互相垂直,说法正确;
C、两条平行线被第三条直线所截,同旁内角的平分线互相垂直,说法正确;
D、在同一个平面内,经过直线外一点,有且只有一条直线与这条直线垂直,说法正确;
故选:A.
2.解:已知A盒中没有装红球,而B盒中装着蓝球,则A盒装的是黄球,C盒装的是红球;
由于乙没有得到B盒,也没有得到黄球,因此乙得到的是C盒;
由于甲没有得到A盒,因此丙得到的是A盒,装的是黄球.故选A.
3.解:A、过已知直线外一点能作已知直线的一条平行线,故本选项错误;
B、过一点能作已知直线的一条垂线,正确;
C、射线AB的端点是A,故本选项错误;
D、点可以用一个大写字母表示,不可用小写字母表示,故本选项错误.
故选:B.
4.解:A、钝角三角形是斜三角形,正确,不符合题意;
B、在一个三角形中至少有一个内角不小于60°,错误,不符合题意;
C、三角形的没有公共顶点的两个外角的和大于平角,正确,符合题意;
D、三角形的外角中,最小的一个是钝角,那它一定是锐角三角形,正确,不符合题意,
故选:B.
5.解:A、∠3和∠2是直线AB、CD被直线AC所截形成的内错角,内错角相等,可以判断AB∥CD,不符合题意;
B、∠1和∠4是直线AD、BC被直线AC所截形成的内错角,内错角相等,可以判断AD∥BC,不能判断AB∥CD,符合题意;
C、∠B和∠5是直线直线AB、CD被直线BE所截形成的同位角,同位角相等,可以判断AB∥CD,不符合题意;
D、∠D和∠BAD直线直线AB、CD被直线AD所截形成的同旁内角,同旁内角互补,可以判断AB∥CD,不符合题意;
故选:B.
6.解:∵AD∥BC,
∴∠2=∠3,
故选:A.
7.解:根据题意∠A>3∠B,即有∠B<∠A,
又∠C<2∠B<∠A,
所以∠A+∠B+∠C<∠A+∠A+∠A=2∠A,
故有180°<2∠A,
得∠A>90°,
即得△ABC为钝角三角形.
故选:C.
二.填空题
8.解:∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵BE是∠ABC的平分线,
∴∠EBC=∠ABC,
又∵CE是∠BCD的平分线,
∴∠ECB=∠DCB,
∴∠EBC+∠ECB=(∠ABC+∠BCD)=90°,
∴∠BEC=180°﹣(∠EBC+∠ECB)=90°,
∴∠1+∠2=90°.
故答案为:90°.
9.解:由题意得,
解得,
故答案为72°,36°,72°.
10.解:∵∠1=∠2,
∴AB∥CD,
∴∠A+∠ADC=180°,
∵∠A=85°,
∴∠ADC=95°.
故答案为:95°.
11.解:∵∠1=∠4
∴a∥b;
∵∠3+∠2=180°,
∴c∥d.
故答案为:a;b;c;d
12.解:①∵a∥b,b∥c,∴a∥c(平行于同一条直线的两直线平行);
②在同一平面内,∵a⊥b,b⊥c,∴a∥c(垂直于同一条直线的两直线平行).
13.解:16个空瓶可换16÷4=4瓶矿泉水;
4瓶矿泉水喝完后又可得到4个空瓶子,
可换4÷4=1瓶矿泉水;
因此最多可以喝矿泉水4+1=5瓶.
故答案为:5.
14.解:根据命题结论正确与否,命题可分为:真命题和假命题.
三.解答题
15.证明:∵EM平分∠BEF,FN平分∠DFH,
∴∠BEF=2∠MEF,∠DFH=2∠NFH,
∵∠BEF=∠DFH,
∴∠MEF=∠NFH,
∴EM∥FN.
16.解:(1)同旁内角互补,两直线平行,真命题;
(2)如果两条直线平行,那么这两条直线垂直于同一条直线(在同一平面内),真命题;
(3)内错角相等,假命题;例如:∠1与∠2是内错角,但不相等;
(4)面积相等的三角形等底等高,是假命题.例如:底边是2,高是4的三角形与底边是4,高是2的三角形.
17.解:红色.理由如下:小李看到小王、小张戴红色和黄色帽子,则小李可能戴蓝色或红色帽子,若小李戴蓝色帽子,则小王必能说出自己帽子颜色为红色,但小王、小张都无法马上说出自己帽子颜色,所以小李的帽子颜色为红色.
18.解:∠AGE=∠CGF,对顶角相等;
∠AGE=∠ACD,两直线平行,同位角相等;
∠AGE=∠CAB,两直线平行,内错角相等;
∵∠DAC=∠CAB,
∴∠DAC=∠AGE;
∵BC∥AD,
∴∠DAC=∠ACB,
又∵∠DAC=∠AGE,
∴∠AGE=∠ACB;
综上所述,和∠AGE相等的角有:∠CGF,∠ACD,∠CAB,∠DAC,∠ACB.
19.解:在△ABC中,∵AE平分∠BAC,
∴∠CAE=∠BAC,
∵∠B=35°,∠C=45°,
∴∠BAC=100°,∠DAC=45°,
∴∠CAE=50°,
∴∠DAE=∠CAE﹣∠DAC=5°.
20.解:∵∠A+∠B+∠C=180°,
∴∠B+∠C=110°,
∵∠B=∠DEB,∠C=∠DFC,
∴∠B+∠DEB+∠C+∠DFC=220°,
∵∠B+∠DEB+∠C+∠DFC+∠EDB+∠FDC=360°,
∴∠EDB+∠FDC=140°,
即∠EDF=180°﹣140°=40°
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
