福建省三明市普通高中2011-2012学年高二上学期联合命题考试数学(文)试题
文档属性
| 名称 | 福建省三明市普通高中2011-2012学年高二上学期联合命题考试数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 297.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-29 22:18:31 | ||
图片预览



文档简介
(考试时间:2012年1月13上午8:00-10:00 满分:150分)
第I卷(选择题 共60分)
一、选择题(本题共12小题。每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。请将正确答案填在答题卷相应的位置上)
1. 抛物线的准线方程是
A. B. C. D.
2.命题“2和3都是素数”的形式是
A. 简单命题 B. C. D.
3.“” 是“”成立的
A.充分而不必要条件 B.必要而不充分条件
C.充分且必要条件 D.既不充分也不必要条件
4. 某商品销售量(件)与销售价格(元/件)负相关,则其回归方程可能是
A. B. C. D.
5. 某产品分为甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率为,出现丙级品的概率为,则对产品抽查一次抽得正品的概率是
A. B. C. D.
6.已知物体运动的方程是(的单位为(米);的单位为(秒)),则该物体在 秒时的瞬时速度为
A.3. B. 2 C.1 D. 0
7. 若某校高一年级8个班参加合唱比赛的得分如茎叶图所示,
则这组数据的中位数和平均数分别是
A.91.5和91.5 B.91.5和92 C. 91和91.5 D.92和92
8.把89化为五进制数的首位数字是
A.1 B.2 C.3 D.4
9.设双曲线的渐近线方程是,则的值
A. 4 B. 3 C. 2 D. 1
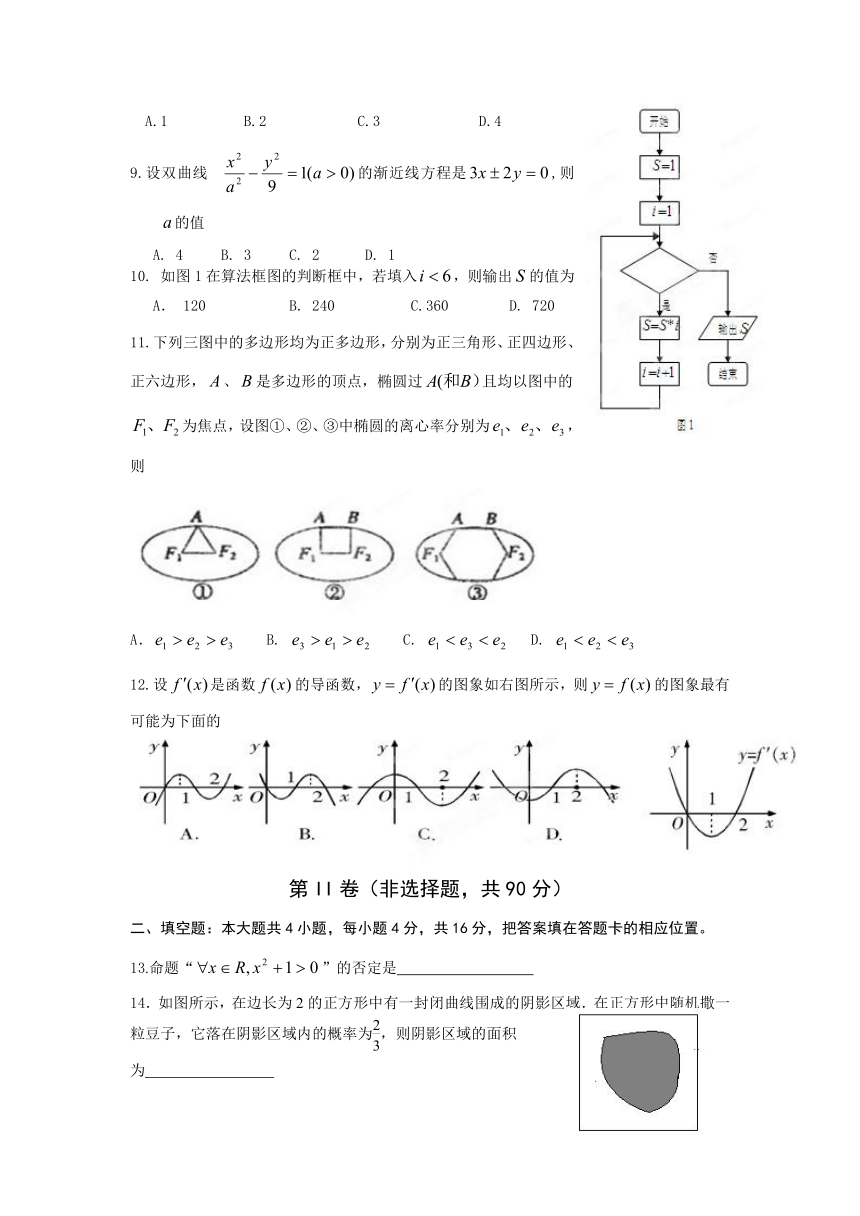
10. 如图1在算法框图的判断框中,若填入,则输出的值为
A. 120 B. 240 C.360 D. 720
11.下列三图中的多边形均为正多边形,分别为正三角形、正四边形、
正六边形,、是多边形的顶点,椭圆过且均以图中的
为焦点,设图①、②、③中椭圆的离心率分别为,
则
A. B. C. D.
12.设是函数的导函数,的图象如右图所示,则的图象最有可能为下面的
第II卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应位置。
13.命题“”的否定是
14.如图所示,在边长为2的正方形中有一封闭曲线围成的阴影区域.在正方形中随机撒一粒豆子,它落在阴影区域内的概率为,则阴影区域的面积
为
15.已知 ,则
16.在△ABC中,、、,给出△ABC满足
的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
条件 方程
①△ABC周长为10 :
②△ABC面积为10 :
③△ABC中,∠A=90° :
则满足条件①、②、③的轨迹方程分别为 (用代号、、填入)
三、解答题 :本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。
6 8 10 12
2 3 5 6
17.(本小题满分12分)某研究机构对高三学生的记忆力和判断力进行统计分析,得到下表数据
(1)请在答题试卷给出的坐标系中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;
(3)试根据(2)中求出的线性回归方程,预测记忆力为9的同学的判断力。
相关公式:,参考数据
18.(本小题满分12分)某校从高二年段学生中随机抽取60名学生,将其期中考试的数学成绩(均为整数)分为六段:[40,50), [50,60),…., [90,100]后得到如下图所示的频率分布直方图。
(1)求分数在[70,80)内的频率;
(2)根据频率分布直方图,估计该校高二年级学生期中考试数学成绩的平均分;
(3)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任意选取两人,求其中恰有一人的分数不低于90分的概率。
19. (本小题满分12分)设函数
(1)求曲线在点处的切线方程;
(2)判断函数零点的个数,并说明理由。
20. (本小题满分12分)已知抛物线:的焦点与双曲线的右焦点重合
(1) 求抛物线的方程;
(2)过点(2,0)作倾斜角为的直线,与抛物线交于、两点,判断是否为直角。若为直角,请给出证明;若不是直角,请说明理由。
21.(本小题满分12分)某工厂生产某种产品,已知该产品的月生产量(吨)与每吨产品的价格(元/吨)之间的关系式为:,且生产吨的成本为(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?
(利润=收入─成本)
22.(本小题满分14分)已知椭圆的中心在原点,一个焦点为,离心率是。
直线(与椭圆交与不同的两点、,以线段为直径作圆,圆心为。
(1)求椭圆的方程;
(2)若圆经过原点,求的值;
(3)在(2)的条件下,设为圆的一条直径,其中、为直径的两端点,点是椭圆上的动点,试求的最大值。
三明市普通高中2011-12学年第一学期联合命题考试
高二文科数学答案
二、填空题
13、; 14、; 15、; 16、;
三、解答题
17.解:(1)如右图………………………………4 分
(2) ∵ ,
且
∴,…………7分
故线性回归直线为 ………………………………9分
(3)由线性回归方程 当时,
所以预测记忆力为9的同学的判断力约为4………………………12分
18. 解:(1)分数在[70,80)内的频率为:
1-(0.010+0.015+0.015+0.025+0.005)10=0.3……………………………….3分
(2)平均分为
……………………………….6分
(3)由题意知[80,90)分数段的人数为人
[90,100)分数段的人数为人
因为用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,所以[80,90)分数段的学生抽取5人,分别记为A,B,C,D,E;[90,100)分数段抽取1人,记为M ………………………………8分
任意选取两人,则有:(A,B),(A,C),(A,D),(A,E),(A,M),(B,C),
所以恰有一人的分数不低于90分的概率为 …………………………12分
19.解:(1)∵
∴ ………………………………………………………2分
(2)由(1)知 ,又﹤0,
∴ 上恒成立, 即在R上单调递增 ……9分
又 (答案不唯一,只需找到函数值异号的一对值即可)
则
故可知函数零点的个数唯一 …………………………12分
(2)依题意,直线的斜率为,
∴ : ……………………………………………………………5分
联立方程 消去得
设,则可知………………………7分
21. 解:设月利润为元,则依题意 ………………………………2分
=
当变化时,、的变化情况如下表
(0,200) 200 (200,)
+ —
↗ 极大值3150000 ↘
……………………………….10分
答:该厂每月生产200吨产品才能使利润达到最大,最大利润是315万元………………12分
22.解:(1)依题意,可设所求的椭圆方程:,半焦距为
(2)联立方程得 ()
所以可知圆E的圆心为(0,),半径为
=(=
又 ,
∴ ==
又,知, 故==
.精品资料。欢迎使用。
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
第I卷(选择题 共60分)
一、选择题(本题共12小题。每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。请将正确答案填在答题卷相应的位置上)
1. 抛物线的准线方程是
A. B. C. D.
2.命题“2和3都是素数”的形式是
A. 简单命题 B. C. D.
3.“” 是“”成立的
A.充分而不必要条件 B.必要而不充分条件
C.充分且必要条件 D.既不充分也不必要条件
4. 某商品销售量(件)与销售价格(元/件)负相关,则其回归方程可能是
A. B. C. D.
5. 某产品分为甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率为,出现丙级品的概率为,则对产品抽查一次抽得正品的概率是
A. B. C. D.
6.已知物体运动的方程是(的单位为(米);的单位为(秒)),则该物体在 秒时的瞬时速度为
A.3. B. 2 C.1 D. 0
7. 若某校高一年级8个班参加合唱比赛的得分如茎叶图所示,
则这组数据的中位数和平均数分别是
A.91.5和91.5 B.91.5和92 C. 91和91.5 D.92和92
8.把89化为五进制数的首位数字是
A.1 B.2 C.3 D.4
9.设双曲线的渐近线方程是,则的值
A. 4 B. 3 C. 2 D. 1
10. 如图1在算法框图的判断框中,若填入,则输出的值为
A. 120 B. 240 C.360 D. 720
11.下列三图中的多边形均为正多边形,分别为正三角形、正四边形、
正六边形,、是多边形的顶点,椭圆过且均以图中的
为焦点,设图①、②、③中椭圆的离心率分别为,
则
A. B. C. D.
12.设是函数的导函数,的图象如右图所示,则的图象最有可能为下面的
第II卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应位置。
13.命题“”的否定是
14.如图所示,在边长为2的正方形中有一封闭曲线围成的阴影区域.在正方形中随机撒一粒豆子,它落在阴影区域内的概率为,则阴影区域的面积
为
15.已知 ,则
16.在△ABC中,、、,给出△ABC满足
的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
条件 方程
①△ABC周长为10 :
②△ABC面积为10 :
③△ABC中,∠A=90° :
则满足条件①、②、③的轨迹方程分别为 (用代号、、填入)
三、解答题 :本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。
6 8 10 12
2 3 5 6
17.(本小题满分12分)某研究机构对高三学生的记忆力和判断力进行统计分析,得到下表数据
(1)请在答题试卷给出的坐标系中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;
(3)试根据(2)中求出的线性回归方程,预测记忆力为9的同学的判断力。
相关公式:,参考数据
18.(本小题满分12分)某校从高二年段学生中随机抽取60名学生,将其期中考试的数学成绩(均为整数)分为六段:[40,50), [50,60),…., [90,100]后得到如下图所示的频率分布直方图。
(1)求分数在[70,80)内的频率;
(2)根据频率分布直方图,估计该校高二年级学生期中考试数学成绩的平均分;
(3)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任意选取两人,求其中恰有一人的分数不低于90分的概率。
19. (本小题满分12分)设函数
(1)求曲线在点处的切线方程;
(2)判断函数零点的个数,并说明理由。
20. (本小题满分12分)已知抛物线:的焦点与双曲线的右焦点重合
(1) 求抛物线的方程;
(2)过点(2,0)作倾斜角为的直线,与抛物线交于、两点,判断是否为直角。若为直角,请给出证明;若不是直角,请说明理由。
21.(本小题满分12分)某工厂生产某种产品,已知该产品的月生产量(吨)与每吨产品的价格(元/吨)之间的关系式为:,且生产吨的成本为(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?
(利润=收入─成本)
22.(本小题满分14分)已知椭圆的中心在原点,一个焦点为,离心率是。
直线(与椭圆交与不同的两点、,以线段为直径作圆,圆心为。
(1)求椭圆的方程;
(2)若圆经过原点,求的值;
(3)在(2)的条件下,设为圆的一条直径,其中、为直径的两端点,点是椭圆上的动点,试求的最大值。
三明市普通高中2011-12学年第一学期联合命题考试
高二文科数学答案
二、填空题
13、; 14、; 15、; 16、;
三、解答题
17.解:(1)如右图………………………………4 分
(2) ∵ ,
且
∴,…………7分
故线性回归直线为 ………………………………9分
(3)由线性回归方程 当时,
所以预测记忆力为9的同学的判断力约为4………………………12分
18. 解:(1)分数在[70,80)内的频率为:
1-(0.010+0.015+0.015+0.025+0.005)10=0.3……………………………….3分
(2)平均分为
……………………………….6分
(3)由题意知[80,90)分数段的人数为人
[90,100)分数段的人数为人
因为用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,所以[80,90)分数段的学生抽取5人,分别记为A,B,C,D,E;[90,100)分数段抽取1人,记为M ………………………………8分
任意选取两人,则有:(A,B),(A,C),(A,D),(A,E),(A,M),(B,C),
所以恰有一人的分数不低于90分的概率为 …………………………12分
19.解:(1)∵
∴ ………………………………………………………2分
(2)由(1)知 ,又﹤0,
∴ 上恒成立, 即在R上单调递增 ……9分
又 (答案不唯一,只需找到函数值异号的一对值即可)
则
故可知函数零点的个数唯一 …………………………12分
(2)依题意,直线的斜率为,
∴ : ……………………………………………………………5分
联立方程 消去得
设,则可知………………………7分
21. 解:设月利润为元,则依题意 ………………………………2分
=
当变化时,、的变化情况如下表
(0,200) 200 (200,)
+ —
↗ 极大值3150000 ↘
……………………………….10分
答:该厂每月生产200吨产品才能使利润达到最大,最大利润是315万元………………12分
22.解:(1)依题意,可设所求的椭圆方程:,半焦距为
(2)联立方程得 ()
所以可知圆E的圆心为(0,),半径为
=(=
又 ,
∴ ==
又,知, 故==
.精品资料。欢迎使用。
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
同课章节目录
