福建省三明市普通高中2011-2012学年高二上学期联合命题考试数学(理)试题
文档属性
| 名称 | 福建省三明市普通高中2011-2012学年高二上学期联合命题考试数学(理)试题 | 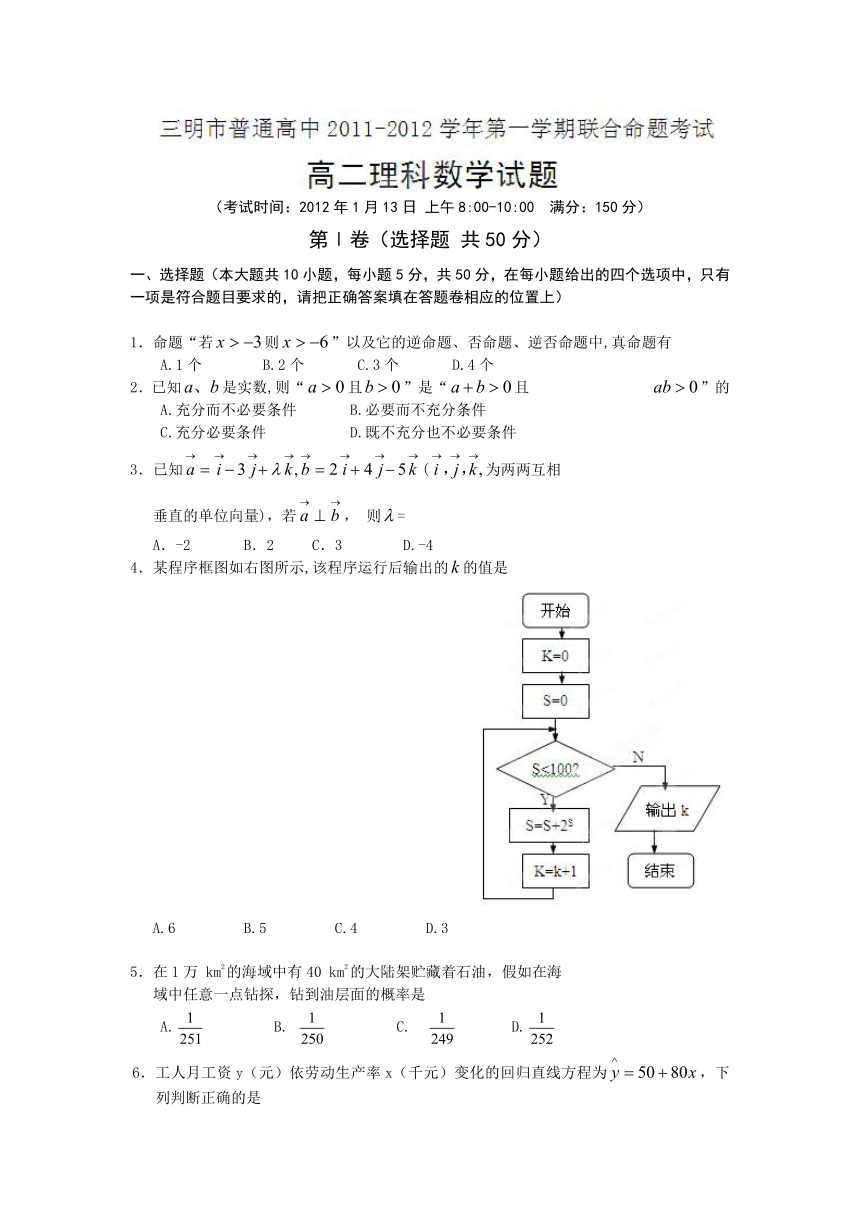 | |
| 格式 | zip | ||
| 文件大小 | 277.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-29 22:18:43 | ||
图片预览





文档简介
(考试时间:2012年1月13日 上午8:00-10:00 满分:150分)
第Ⅰ卷(选择题 共50分)
一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案填在答题卷相应的位置上)
1.命题“若则”以及它的逆命题、否命题、逆否命题中,真命题有
A.1个 B.2个 C.3个 D.4个
2.已知是实数,则“且”是“且 ”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.已知(为两两互相
垂直的单位向量),若, 则=
A.-2 B.2 C.3 D.-4
4.某程序框图如右图所示,该程序运行后输出的的值是
A.6 B.5 C.4 D.3
5.在1万 km2的海域中有40 km2的大陆架贮藏着石油,假如在海
域中任意一点钻探,钻到油层面的概率是
A. B. C. D.
6.工人月工资y(元)依劳动生产率x(千元)变化的回归直线方程为,下列判断正确的是
A.劳动生产率为1000元时,工资为50元 B.劳动生产率提高1000元时,工资提高130元
C.劳动生产率提高1000元时,工资提高80元 D.劳动生产率为1000元时,工资为80元
7.从3男1女4位同学中选派2位同学参加某演讲比赛,那么选派的都是男生的概率是
A. B. C. D.
8.已知椭圆与双曲线有相同的焦点,则的值是
A.1 B.2 C.3 D. 4
9.已知空间四边形,其对角线为分别是的中点,点在线段上,且,若,则的值为
A. B. C. D.
10.设是函数的导函数,将和的图像画在同一个直角坐标系中,不可能的是
第Ⅱ卷(非选择题 共100分)
二、填空题(本大题共5小题,每小题4分,共20分。请将答案填在答题卷相应的位置上)
11.直线,曲线及轴所围图形的面积为
12.曲线在点处的切线方程为
13.在调查高一年级1500名学生的身高的过程中,抽取了一个样本并将其分组画成频率分布直方图,[160cm,165cm]组的小矩形的高为0.01,[165cm,170cm]组小矩形的高为0.05,试估计该高一年集学生身高在[160cm,170cm]范围内的人数
14.已知抛物线过其焦点的直线交抛物线于两点,过中点作
轴垂线交轴于点,若,则=
15.已知双曲线的左焦点为,点为双曲线右支上一点,且与圆相切于点,为线段的中点,为坐标原点,则=
三、解答题(本大题共6小题,共80分。解答应写出文字说明、推理过程或演算步骤。请在答题卷相应题目的答题区域内作答)
16.(本小题满分13分)
从甲、乙两个班中各随机的抽取6名学生,他们的数学成绩如下:
甲班 76 74 82 96 66 76
乙班 86 84 62 76 78 92
(I)画出茎叶图并求出甲班学生的数学成绩的中位数;
(II)若不低于80分则表示该生数学成绩为优秀。现从甲、乙两班中各抽出1名学生参加数学兴趣小组,求这两名学生的数学成绩恰好都优秀的概率。
17.(本小题满分13分)
已知命题:方程表示焦点在y轴上的椭圆; 命题:直线
与抛物线 有两个交点
(I)若为真命题,求实数的取值范围
(II)若,求实数的取值范围。
18.(本小题满分13分)
如图,正方形所在的平面与平面垂直, 是和的交点,
且,
(I)求证:
(II)求直线与平面所成的角的大小;
(III)求锐二面角的大小.
19.(本小题满分13分)
已知椭圆(a>b>0)的离心率 为
该椭圆上一点,
(I)求椭圆的方程.
(II)过点作直线与椭圆相交于点,若以为直径的圆经原点,求直线的方程
20. (本小题满分14分)
某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划成一个矩形高科技工业园区.已知且,曲线段是以点为顶点且开口向右的抛物线的一段.
(I)建立适当的坐标系,求曲线段的方程;
(II)如果要使矩形的相邻两边分别落在上,且一个顶点落在曲线段上,问如何规划才能使矩形工业园区的用地面积最大 并求这个最大值.
21. (本小题满分14分)
已知函数.
(I) 若函数在处取得极值为-1.求、的值;
(II)若,求的单调区间
(III)在(I)的条件下令,常数,若的图象与轴交于、两点,线段的中点为,求证:
三明市普通高中2011-2012学年第一学期联合命题考试
高二理科数学试题参考答案及评分标准
一、选择题(每小题5分,共50分)
二、填空题(每小题4分,共20分)
11、2ln2 12、 .y=2x+3; 13、 450 14、 8 15、-1
甲班 乙班
6 6 2
6 4 6 7 6 8
2 8 6 4 ……………………… 5分
6 9 2
甲班学生的数学成绩的中位数是76 ……………………… 7分
∴这两名学生的数学成绩都优秀的概率是……………………… 13分
17、(I) 由得……………………………..2分
∵为真命题
方程有两个不相等的实数根
(II) ∵,都是真命题……………………………………….8分
∴方程表示焦点在y轴上的椭圆
∴ ……………………… 10分
即时………………………………………………………….13分
18、依题可知,CA,CB,CD两两垂直,故可建立如图空间直角坐标系C-xyz,设正方形
边长为1,则AC=BC=1-…………………2分
C(0,0,0),A(1,0,0),B(0,1,0),D(0,0,1),E(1,0,1),
M()
(I)
(II)由(I)知为面EBC的一个法向量,,设所求角大小为,则
取,
所以锐二面角A—BE—C的大小为…………………13分
∴椭圆的标准方程是………………………………………………5分
(II) 设依题设直线的方程为
整理得,…………………………………6分
于是,.……………………………7分
……………………………8分
由知.将(1)式和(2)式代入得
解得
20、.(I) 以O为原点,OA所在直线为y轴建立直角坐标系(如图),
依题可设抛物线方程为y2=2px(p>0),且C(4,2).由此可得,
故曲线段OC的方程为y2=x().……………………………6分
(II) 设P(t2,t)(),
则在矩形PQBN中,|PQ|=2+t,|PN|=4-t2.
工业园区面积S(t)=|PQ||PN|=(2+t)( 4-t2)= -t3-2t2+4t+8.
……………………………8分
导数= -3t2-4t+4,
当时,; 当时,.
答:当矩形的长为km,宽为km时,园区面积最大,最大值为km2.-----14分
21、(I)由题意可知:所以………………4分
当时,时,,单调增,
时,,单调减………………9分
两式相减得:
则 ………………10分
, 令,则]
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
O
A
B
C
A
B
C
D
E
M
x
y
z
O
y
x
A
B
C
Q
P
N
第Ⅰ卷(选择题 共50分)
一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案填在答题卷相应的位置上)
1.命题“若则”以及它的逆命题、否命题、逆否命题中,真命题有
A.1个 B.2个 C.3个 D.4个
2.已知是实数,则“且”是“且 ”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.已知(为两两互相
垂直的单位向量),若, 则=
A.-2 B.2 C.3 D.-4
4.某程序框图如右图所示,该程序运行后输出的的值是
A.6 B.5 C.4 D.3
5.在1万 km2的海域中有40 km2的大陆架贮藏着石油,假如在海
域中任意一点钻探,钻到油层面的概率是
A. B. C. D.
6.工人月工资y(元)依劳动生产率x(千元)变化的回归直线方程为,下列判断正确的是
A.劳动生产率为1000元时,工资为50元 B.劳动生产率提高1000元时,工资提高130元
C.劳动生产率提高1000元时,工资提高80元 D.劳动生产率为1000元时,工资为80元
7.从3男1女4位同学中选派2位同学参加某演讲比赛,那么选派的都是男生的概率是
A. B. C. D.
8.已知椭圆与双曲线有相同的焦点,则的值是
A.1 B.2 C.3 D. 4
9.已知空间四边形,其对角线为分别是的中点,点在线段上,且,若,则的值为
A. B. C. D.
10.设是函数的导函数,将和的图像画在同一个直角坐标系中,不可能的是
第Ⅱ卷(非选择题 共100分)
二、填空题(本大题共5小题,每小题4分,共20分。请将答案填在答题卷相应的位置上)
11.直线,曲线及轴所围图形的面积为
12.曲线在点处的切线方程为
13.在调查高一年级1500名学生的身高的过程中,抽取了一个样本并将其分组画成频率分布直方图,[160cm,165cm]组的小矩形的高为0.01,[165cm,170cm]组小矩形的高为0.05,试估计该高一年集学生身高在[160cm,170cm]范围内的人数
14.已知抛物线过其焦点的直线交抛物线于两点,过中点作
轴垂线交轴于点,若,则=
15.已知双曲线的左焦点为,点为双曲线右支上一点,且与圆相切于点,为线段的中点,为坐标原点,则=
三、解答题(本大题共6小题,共80分。解答应写出文字说明、推理过程或演算步骤。请在答题卷相应题目的答题区域内作答)
16.(本小题满分13分)
从甲、乙两个班中各随机的抽取6名学生,他们的数学成绩如下:
甲班 76 74 82 96 66 76
乙班 86 84 62 76 78 92
(I)画出茎叶图并求出甲班学生的数学成绩的中位数;
(II)若不低于80分则表示该生数学成绩为优秀。现从甲、乙两班中各抽出1名学生参加数学兴趣小组,求这两名学生的数学成绩恰好都优秀的概率。
17.(本小题满分13分)
已知命题:方程表示焦点在y轴上的椭圆; 命题:直线
与抛物线 有两个交点
(I)若为真命题,求实数的取值范围
(II)若,求实数的取值范围。
18.(本小题满分13分)
如图,正方形所在的平面与平面垂直, 是和的交点,
且,
(I)求证:
(II)求直线与平面所成的角的大小;
(III)求锐二面角的大小.
19.(本小题满分13分)
已知椭圆(a>b>0)的离心率 为
该椭圆上一点,
(I)求椭圆的方程.
(II)过点作直线与椭圆相交于点,若以为直径的圆经原点,求直线的方程
20. (本小题满分14分)
某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划成一个矩形高科技工业园区.已知且,曲线段是以点为顶点且开口向右的抛物线的一段.
(I)建立适当的坐标系,求曲线段的方程;
(II)如果要使矩形的相邻两边分别落在上,且一个顶点落在曲线段上,问如何规划才能使矩形工业园区的用地面积最大 并求这个最大值.
21. (本小题满分14分)
已知函数.
(I) 若函数在处取得极值为-1.求、的值;
(II)若,求的单调区间
(III)在(I)的条件下令,常数,若的图象与轴交于、两点,线段的中点为,求证:
三明市普通高中2011-2012学年第一学期联合命题考试
高二理科数学试题参考答案及评分标准
一、选择题(每小题5分,共50分)
二、填空题(每小题4分,共20分)
11、2ln2 12、 .y=2x+3; 13、 450 14、 8 15、-1
甲班 乙班
6 6 2
6 4 6 7 6 8
2 8 6 4 ……………………… 5分
6 9 2
甲班学生的数学成绩的中位数是76 ……………………… 7分
∴这两名学生的数学成绩都优秀的概率是……………………… 13分
17、(I) 由得……………………………..2分
∵为真命题
方程有两个不相等的实数根
(II) ∵,都是真命题……………………………………….8分
∴方程表示焦点在y轴上的椭圆
∴ ……………………… 10分
即时………………………………………………………….13分
18、依题可知,CA,CB,CD两两垂直,故可建立如图空间直角坐标系C-xyz,设正方形
边长为1,则AC=BC=1-…………………2分
C(0,0,0),A(1,0,0),B(0,1,0),D(0,0,1),E(1,0,1),
M()
(I)
(II)由(I)知为面EBC的一个法向量,,设所求角大小为,则
取,
所以锐二面角A—BE—C的大小为…………………13分
∴椭圆的标准方程是………………………………………………5分
(II) 设依题设直线的方程为
整理得,…………………………………6分
于是,.……………………………7分
……………………………8分
由知.将(1)式和(2)式代入得
解得
20、.(I) 以O为原点,OA所在直线为y轴建立直角坐标系(如图),
依题可设抛物线方程为y2=2px(p>0),且C(4,2).由此可得,
故曲线段OC的方程为y2=x().……………………………6分
(II) 设P(t2,t)(),
则在矩形PQBN中,|PQ|=2+t,|PN|=4-t2.
工业园区面积S(t)=|PQ||PN|=(2+t)( 4-t2)= -t3-2t2+4t+8.
……………………………8分
导数= -3t2-4t+4,
当时,; 当时,.
答:当矩形的长为km,宽为km时,园区面积最大,最大值为km2.-----14分
21、(I)由题意可知:所以………………4分
当时,时,,单调增,
时,,单调减………………9分
两式相减得:
则 ………………10分
, 令,则]
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
O
A
B
C
A
B
C
D
E
M
x
y
z
O
y
x
A
B
C
Q
P
N
同课章节目录
