2020-2021学年八年级数学华东师大版下册第17章17.3一次函数 培优试题 (Word版含答案)
文档属性
| 名称 | 2020-2021学年八年级数学华东师大版下册第17章17.3一次函数 培优试题 (Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 23:18:33 | ||
图片预览




文档简介
2020—2021学年八年级数学华东师大版下册第17章(17.3一次函数)培优试题与简答
一.选择题(共10小题,每小题2分,共20分)
1.若函数是正比例函数,则
A. B. C. D.
2.下列函数中,不是一次函数的是
A. B. C. D.
3.已知函数的图象大致如图所示,则函数的图象大致是
A. B.
C. D.
4.若一次函数的图象经过第一、二、四象限,则
A., B., C., D.,
5.已知点,都在直线上,则,的值的大小关系是
A. B. C. D.不能确定
6.将直线沿轴向下平移3个单位长度,平移后的直线所对应的函数关系式
A. B. C. D.
7.下列关于一次函数的图象的说法中,错误的是
A.函数图象经过第一、二、四象限 B.函数图象与轴的交点坐标为
C.当时, D.的值随着值的增大而减小
8.在直角坐标系中,点、、在同一条直线上,则的值是
A. B.6 C.6或3 D.6或
9.如图,直线经过点,当,则的取值范围是
A. B. C. D.
10.周末,小明骑自行车从家里出发去游玩.从家出发1小时后到达迪诺水镇,游玩一段时间后按原速前往万达广场.小明离家1小时50分钟后,妈妈驾车沿相同路线前往万达广场.妈妈出发25分钟时,恰好在万达广场门口追上小明.如图是他们离家的路程与小明离家时间的函数图象,则下列说法中正确的是
A.小明在迪诺水镇游玩后,经过到达万达广场
B.小明的速度是,妈妈的速度是
C.万达广场离小明家
D.点的坐标为,
二.填空题(共8小题,每小题3分,共24分)
11.点在函数的图象上,则代数式的值等于 .
12.将函数的图象向下平移2个单位,得到的图象的函数表达式是 .
13.如果一次函数的图象经过第一、二、四象限,那么常数的取值范围为 .
14.已知一次函数,当时,的最大值是 .
15.已知关于、的二元一次方程组的解是,则一次函数和的图象交点坐标为 .
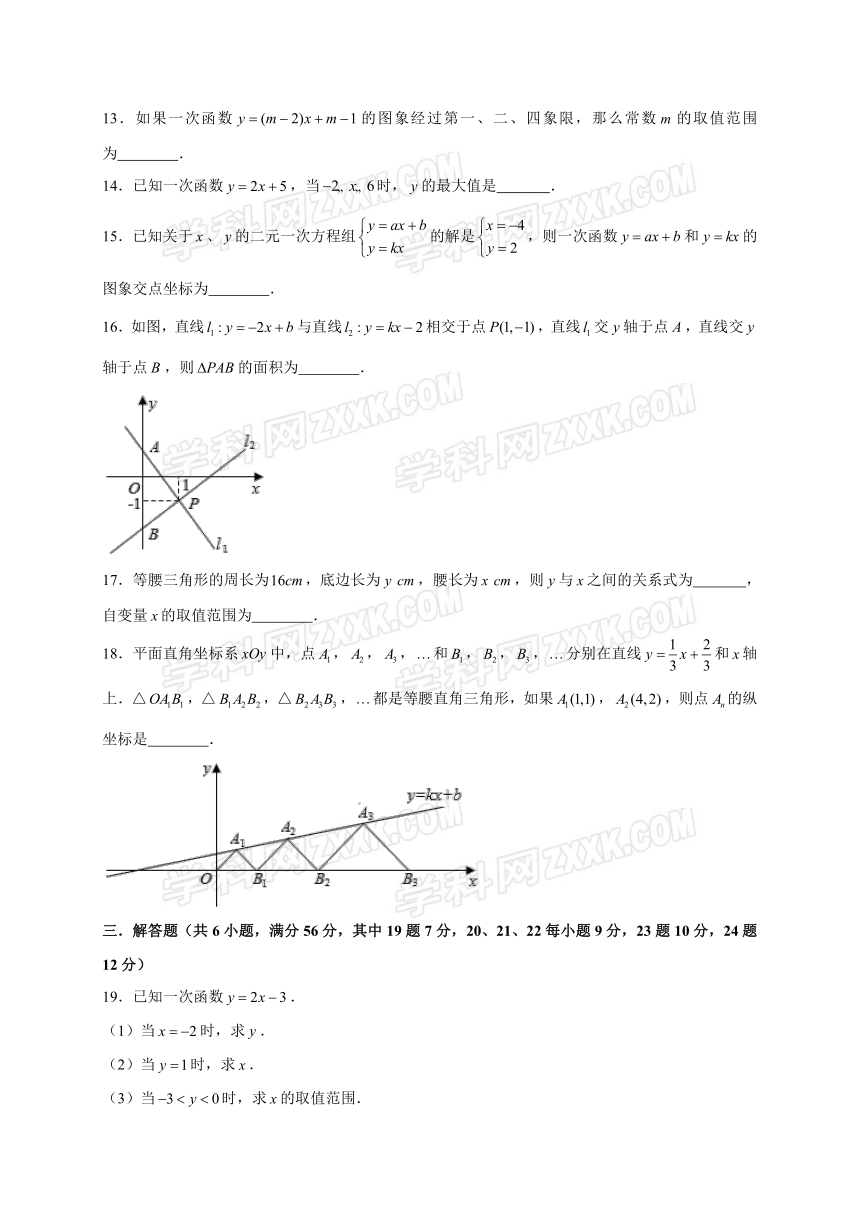
16.如图,直线与直线相交于点,直线交轴于点,直线交轴于点,则的面积为 .
17.等腰三角形的周长为,底边长为,腰长为,则与之间的关系式为 ,自变量的取值范围为 .
18.平面直角坐标系中,点,,,和,,,分别在直线和轴上.△,△,△,都是等腰直角三角形,如果,,则点的纵坐标是 .
三.解答题(共6小题,满分56分,其中19题7分,20、21、22每小题9分,23题10分,24题12分)
19.已知一次函数.
(1)当时,求.
(2)当时,求.
(3)当时,求的取值范围.
20.如图,一次函数图象分别与轴正半轴、轴负半轴相交于点、.
(1)求的取值范围;
(2)若该一次函数的图象向上平移4个单位长度后可得某正比例函数的图象,试求这个正比例函数的解析式.
21.如图,已知一次函数的图象经过,两点,并且交轴于点,交轴于点.
(1)求一次函数的解析式;
(2)求点和点的坐标;
(3)求的面积
22.已知点、在直线上,直线和函数的图象交于点.
(1)求直线的表达式;
(2)若点的横坐标是1,求关于、的方程组的解及的值.
(3)在(2)的条件下,根据图象比较当时,的值与的值的大小.
23.在”新冠病毒”防控期间,某益康医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售,两次购进同一商品的进价相同,具体情况如表所示:
(1)求酒精消毒液和测温枪两种商品每件的进价分别是多少元?
(2)公司决定酒精消毒液以每件20元出售,测温枪以每件240元出售.为满足市场需求,需购进这两种商品共1000件,且酒精消毒液的数量不少于测温枪数量的4倍,求该公司销售完上述1000件商品获得的最大利润.
项目 购进数量(件 购进所需费用(元
酒精消毒液 测温枪
第一次 30 40 8300
第二次 40 30 6400
24.如图,在平面直角坐标系中,过点的直线与直线相交于点.
(1)求直线的表达式;
(2)求的面积;
(3)动点在线段和射线上运动,是否存在点,使的面积是的面积的?若存在,求出此时点的坐标;若不存在,请说明理由.
2020—2021学年八年级数学华东师大版下册第17章(17.3一次函数)培优试题参考简答
一.选择题(共10小题)
1.. 2.. 3.. 4.. 5.. 6.. 7.. 8..
9.. 10..
二.填空题(共8小题)
11. . 12. . 13. . 14. 17 . 15. .16. . 17. , . 18. .
三.解答题(共6小题)
19.已知一次函数.
(1)当时,求.
(2)当时,求.
(3)当时,求的取值范围.
【解】:(1)把代入中得:;
(2)把代入中得:,
解得:;
(3),
,
, 解得:.
20.如图,一次函数图象分别与轴正半轴、轴负半轴相交于点、.
(1)求的取值范围;
(2)若该一次函数的图象向上平移4个单位长度后可得某正比例函数的图象,试求这个正比例函数的解析式.
【解】:(1)由题意知,一次函数图象经过第一、三、四象限,
, 解得;
(2)将的图象向上平移4个单位长度后得,
由题意得,,
解得,
这个正比例函数的解析式为.
21.如图,已知一次函数的图象经过,两点,并且交轴于点,交轴于点.
(1)求一次函数的解析式;
(2)求点和点的坐标;
(3)求的面积
【解】:(1)把,代入得, 解得.
所以一次函数解析式为;
(2)令,则,解得,
所以点的坐标为,
把代入得,
所以点坐标为,
(3).
22.已知点、在直线上,直线和函数的图象交于点.
(1)求直线的表达式;
(2)若点的横坐标是1,求关于、的方程组的解及的值.
(3)在(2)的条件下,根据图象比较当时,的值与的值的大小.
【解】:(1)把、代入得,解得,
直线的解析式为;
(2)当时,,则,
直线和函数的图象交于点.
关于、的方程组的解为;
把代入得,解得;
(3)当时,.
23.在”新冠病毒”防控期间,某益康医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售,两次购进同一商品的进价相同,具体情况如表所示:
(1)求酒精消毒液和测温枪两种商品每件的进价分别是多少元?
(2)公司决定酒精消毒液以每件20元出售,测温枪以每件240元出售.为满足市场需求,需购进这两种商品共1000件,且酒精消毒液的数量不少于测温枪数量的4倍,求该公司销售完上述1000件商品获得的最大利润.
项目 购进数量(件 购进所需费用(元
酒精消毒液 测温枪
第一次 30 40 8300
第二次 40 30 6400
【解】:(1)设酒精消毒液每件的进价为元,测温枪每件的进价为元,
根据题意得:, 解得:.
酒精消毒液每件的进价为10元,测温枪每件的进价为200元.
(2)设购进测温枪件,获得的利润为元,则购进酒精消毒液件,
根据题意得:
,
酒精消毒液的数量不少于测温枪数量的4倍,
,
解得:.
又在中,,
的值随的增大而增大,
当时,取最大值,最大值为,
当购进酒精消毒液800件、购进测温枪200件时,销售利润最大,最大利润为16000元.
24.如图,在平面直角坐标系中,过点的直线与直线相交于点.
(1)求直线的表达式;
(2)求的面积;
(3)动点在线段和射线上运动,是否存在点,使的面积是的面积的?若存在,求出此时点的坐标;若不存在,请说明理由.
【解】:(1)设直线的解析式是,
根据题意得:, 解得:.
则直线的解析式是:;
(2),,
,
;
(3)设的解析式是,则,
解得:.
则直线的解析式是:,
当的面积是的面积的时,
到轴的距离是,
点的横坐标为2或;
当的横坐标是2时,
在中,当时,,则的坐标是;
在中,则,则的坐标是.
则的坐标是:或.
当的横坐标是时,
在中,当时,,则的坐标是.
综上所述:的坐标是:或或.
一.选择题(共10小题,每小题2分,共20分)
1.若函数是正比例函数,则
A. B. C. D.
2.下列函数中,不是一次函数的是
A. B. C. D.
3.已知函数的图象大致如图所示,则函数的图象大致是
A. B.
C. D.
4.若一次函数的图象经过第一、二、四象限,则
A., B., C., D.,
5.已知点,都在直线上,则,的值的大小关系是
A. B. C. D.不能确定
6.将直线沿轴向下平移3个单位长度,平移后的直线所对应的函数关系式
A. B. C. D.
7.下列关于一次函数的图象的说法中,错误的是
A.函数图象经过第一、二、四象限 B.函数图象与轴的交点坐标为
C.当时, D.的值随着值的增大而减小
8.在直角坐标系中,点、、在同一条直线上,则的值是
A. B.6 C.6或3 D.6或
9.如图,直线经过点,当,则的取值范围是
A. B. C. D.
10.周末,小明骑自行车从家里出发去游玩.从家出发1小时后到达迪诺水镇,游玩一段时间后按原速前往万达广场.小明离家1小时50分钟后,妈妈驾车沿相同路线前往万达广场.妈妈出发25分钟时,恰好在万达广场门口追上小明.如图是他们离家的路程与小明离家时间的函数图象,则下列说法中正确的是
A.小明在迪诺水镇游玩后,经过到达万达广场
B.小明的速度是,妈妈的速度是
C.万达广场离小明家
D.点的坐标为,
二.填空题(共8小题,每小题3分,共24分)
11.点在函数的图象上,则代数式的值等于 .
12.将函数的图象向下平移2个单位,得到的图象的函数表达式是 .
13.如果一次函数的图象经过第一、二、四象限,那么常数的取值范围为 .
14.已知一次函数,当时,的最大值是 .
15.已知关于、的二元一次方程组的解是,则一次函数和的图象交点坐标为 .
16.如图,直线与直线相交于点,直线交轴于点,直线交轴于点,则的面积为 .
17.等腰三角形的周长为,底边长为,腰长为,则与之间的关系式为 ,自变量的取值范围为 .
18.平面直角坐标系中,点,,,和,,,分别在直线和轴上.△,△,△,都是等腰直角三角形,如果,,则点的纵坐标是 .
三.解答题(共6小题,满分56分,其中19题7分,20、21、22每小题9分,23题10分,24题12分)
19.已知一次函数.
(1)当时,求.
(2)当时,求.
(3)当时,求的取值范围.
20.如图,一次函数图象分别与轴正半轴、轴负半轴相交于点、.
(1)求的取值范围;
(2)若该一次函数的图象向上平移4个单位长度后可得某正比例函数的图象,试求这个正比例函数的解析式.
21.如图,已知一次函数的图象经过,两点,并且交轴于点,交轴于点.
(1)求一次函数的解析式;
(2)求点和点的坐标;
(3)求的面积
22.已知点、在直线上,直线和函数的图象交于点.
(1)求直线的表达式;
(2)若点的横坐标是1,求关于、的方程组的解及的值.
(3)在(2)的条件下,根据图象比较当时,的值与的值的大小.
23.在”新冠病毒”防控期间,某益康医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售,两次购进同一商品的进价相同,具体情况如表所示:
(1)求酒精消毒液和测温枪两种商品每件的进价分别是多少元?
(2)公司决定酒精消毒液以每件20元出售,测温枪以每件240元出售.为满足市场需求,需购进这两种商品共1000件,且酒精消毒液的数量不少于测温枪数量的4倍,求该公司销售完上述1000件商品获得的最大利润.
项目 购进数量(件 购进所需费用(元
酒精消毒液 测温枪
第一次 30 40 8300
第二次 40 30 6400
24.如图,在平面直角坐标系中,过点的直线与直线相交于点.
(1)求直线的表达式;
(2)求的面积;
(3)动点在线段和射线上运动,是否存在点,使的面积是的面积的?若存在,求出此时点的坐标;若不存在,请说明理由.
2020—2021学年八年级数学华东师大版下册第17章(17.3一次函数)培优试题参考简答
一.选择题(共10小题)
1.. 2.. 3.. 4.. 5.. 6.. 7.. 8..
9.. 10..
二.填空题(共8小题)
11. . 12. . 13. . 14. 17 . 15. .16. . 17. , . 18. .
三.解答题(共6小题)
19.已知一次函数.
(1)当时,求.
(2)当时,求.
(3)当时,求的取值范围.
【解】:(1)把代入中得:;
(2)把代入中得:,
解得:;
(3),
,
, 解得:.
20.如图,一次函数图象分别与轴正半轴、轴负半轴相交于点、.
(1)求的取值范围;
(2)若该一次函数的图象向上平移4个单位长度后可得某正比例函数的图象,试求这个正比例函数的解析式.
【解】:(1)由题意知,一次函数图象经过第一、三、四象限,
, 解得;
(2)将的图象向上平移4个单位长度后得,
由题意得,,
解得,
这个正比例函数的解析式为.
21.如图,已知一次函数的图象经过,两点,并且交轴于点,交轴于点.
(1)求一次函数的解析式;
(2)求点和点的坐标;
(3)求的面积
【解】:(1)把,代入得, 解得.
所以一次函数解析式为;
(2)令,则,解得,
所以点的坐标为,
把代入得,
所以点坐标为,
(3).
22.已知点、在直线上,直线和函数的图象交于点.
(1)求直线的表达式;
(2)若点的横坐标是1,求关于、的方程组的解及的值.
(3)在(2)的条件下,根据图象比较当时,的值与的值的大小.
【解】:(1)把、代入得,解得,
直线的解析式为;
(2)当时,,则,
直线和函数的图象交于点.
关于、的方程组的解为;
把代入得,解得;
(3)当时,.
23.在”新冠病毒”防控期间,某益康医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售,两次购进同一商品的进价相同,具体情况如表所示:
(1)求酒精消毒液和测温枪两种商品每件的进价分别是多少元?
(2)公司决定酒精消毒液以每件20元出售,测温枪以每件240元出售.为满足市场需求,需购进这两种商品共1000件,且酒精消毒液的数量不少于测温枪数量的4倍,求该公司销售完上述1000件商品获得的最大利润.
项目 购进数量(件 购进所需费用(元
酒精消毒液 测温枪
第一次 30 40 8300
第二次 40 30 6400
【解】:(1)设酒精消毒液每件的进价为元,测温枪每件的进价为元,
根据题意得:, 解得:.
酒精消毒液每件的进价为10元,测温枪每件的进价为200元.
(2)设购进测温枪件,获得的利润为元,则购进酒精消毒液件,
根据题意得:
,
酒精消毒液的数量不少于测温枪数量的4倍,
,
解得:.
又在中,,
的值随的增大而增大,
当时,取最大值,最大值为,
当购进酒精消毒液800件、购进测温枪200件时,销售利润最大,最大利润为16000元.
24.如图,在平面直角坐标系中,过点的直线与直线相交于点.
(1)求直线的表达式;
(2)求的面积;
(3)动点在线段和射线上运动,是否存在点,使的面积是的面积的?若存在,求出此时点的坐标;若不存在,请说明理由.
【解】:(1)设直线的解析式是,
根据题意得:, 解得:.
则直线的解析式是:;
(2),,
,
;
(3)设的解析式是,则,
解得:.
则直线的解析式是:,
当的面积是的面积的时,
到轴的距离是,
点的横坐标为2或;
当的横坐标是2时,
在中,当时,,则的坐标是;
在中,则,则的坐标是.
则的坐标是:或.
当的横坐标是时,
在中,当时,,则的坐标是.
综上所述:的坐标是:或或.
