2019-2020学年黑龙江省哈尔滨四十七中八年级下期月考数学试卷(3月份)(五四学制)(word版含解析)
文档属性
| 名称 | 2019-2020学年黑龙江省哈尔滨四十七中八年级下期月考数学试卷(3月份)(五四学制)(word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 449.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 00:00:00 | ||
图片预览

文档简介
2019-2020学年黑龙江省哈尔滨四十七中八年级(下)月考数学试卷(3月份)(五四学制)
一、选择题(每小题3分,共计30分)
1.下面选项中的四边形不是轴对称图形的是( )
A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
2.在直角坐标系中,点P(﹣2,3)到原点的距离是( )
A. B. C. D.2
3.下列四组线段中,可以构成直角三角形的是 ( )
A.1、2、3 B.3、4、5 C.1、1、 D.6、7、8
4.在?ABCD中,∠A:∠B=7:2,则∠C等于( )
A.40° B.80° C.120° D.140°
5.如图,?ABCD中,∠DAB的平分线AE交CD于E,AB=5,BC=3,则EC的长( )
A.1 B.l.5 C.2 D.3
6.如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD C.OA=OB D.OA=AD
7.平行四边形和矩形都具有的性质是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.每条对角线平分一组对角
8.如图,在Rt△ABC中,∠B=90°,BC=12,AB=5,则斜边上的中线BO长是( )
A.2.5 B.4 C.6 D.6.5
9.如图,在Rt△ABC中,∠BAC=90°,点D在BC上,过D作DF⊥BC交BA的延长线于F,连接AD,CF,若∠CFE=32°,∠ADB=45°,则∠B的大小是( )
A.32° B.64° C.77° D.87°
10.在矩形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD交BC于点E,∠CAE=15°,连接OE,则下面的结论:其中正确的结论有( )
①△DOC是等边三角形;
②△BOE是等腰三角形;
③BC=2AB;
④∠AOE=150°;
⑤S△AOE=S△COE.
A.2 个 B.3个 C.4 个 D.5个
二、填空题(每小题3分,共计30分)
11.在?ABCD中,如果∠A+∠C=140°,那么∠C等于 .
12.平行四边形的周长等于16cm,两邻边长的比为3:1,那么这个平行四边形较长的边长为 cm.
13.在△ABC中,∠C=90°,∠A=45°,AC=2,斜边AB的长为 .
14.如图,以直角三角形ABC的三边向外作正方形,三个正方形的面积分别为S1,S2,S3,若S1=9,S2=16,则S3= .
15.如图,在?ABCD中,AB=,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为 .
16.一个三角形的面积是12,则连接这个三角形各边中点围成的三角形的面积是 .
17.一架长为10m的梯子,斜靠在竖直的墙上,这时梯子的底端与墙的距离为6m,如果梯子顶端沿墙下滑2m,那么梯子底端将滑动 m.
18.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH= .
19.在?ABCD中,AB=5,AC=,BC边上的高为4,则BC= .
20.在矩形ABCD中,点E、F分别在AB、AD上,CD=9,CE=20,∠EFB=2∠AFE=2∠BCE,则线段AF的长为 .
三、解答题(其中21~22题各7分,23~24题各8分,25~27题各10分,共计60分)21.先化简,再求值:÷﹣,其中x=﹣2.
22.如图,正方形网格中的每个小正方形边长都是1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画图:
(1)在图①中画一个面积为18的正方形;
(2)在图②中画一个面积为12的菱形,并直接写出所画菱形的周长.
23.如图所示的一块地ABCD,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m,求这块地的面积.
24.在△ABC中,AD⊥BC于点D,点E为AC边的中点,过点A作AF∥BC,交DE的延长线于点F,连接CF.
(1)如图1,求证:四边形ADCF是矩形;
(2)如图2,当AB=AC时,取AB的中点G,连接DG、EG,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形ADCF).
25.植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
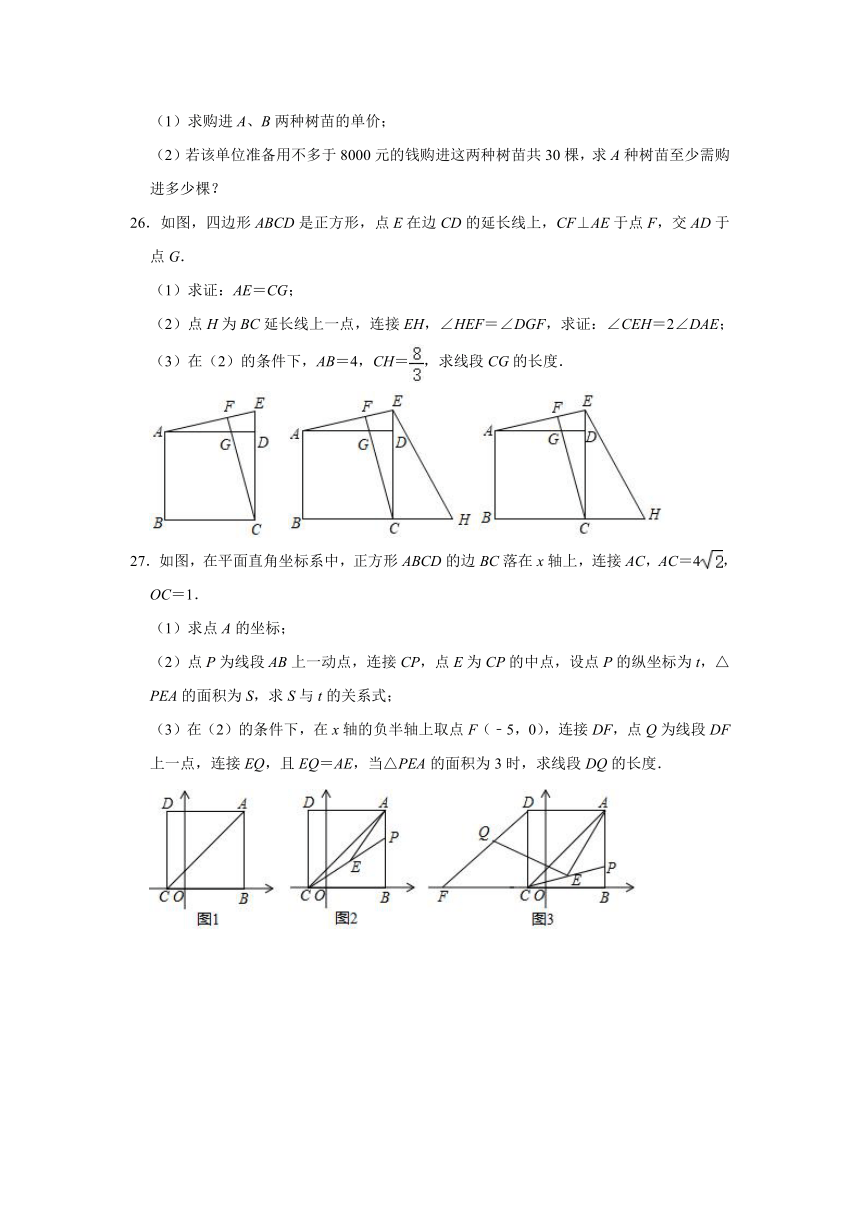
26.如图,四边形ABCD是正方形,点E在边CD的延长线上,CF⊥AE于点F,交AD于点G.
(1)求证:AE=CG;
(2)点H为BC延长线上一点,连接EH,∠HEF=∠DGF,求证:∠CEH=2∠DAE;
(3)在(2)的条件下,AB=4,CH=,求线段CG的长度.
27.如图,在平面直角坐标系中,正方形ABCD的边BC落在x轴上,连接AC,AC=4,OC=1.
(1)求点A的坐标;
(2)点P为线段AB上一动点,连接CP,点E为CP的中点,设点P的纵坐标为t,△PEA的面积为S,求S与t的关系式;
(3)在(2)的条件下,在x轴的负半轴上取点F(﹣5,0),连接DF,点Q为线段DF上一点,连接EQ,且EQ=AE,当△PEA的面积为3时,求线段DQ的长度.
2019-2020学年黑龙江省哈尔滨四十七中八年级(下)月考数学试卷(3月份)(五四学制)
参考答案与试题解析
一.选择题(共10小题)
1.下面选项中的四边形不是轴对称图形的是( )
A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
【分析】根据轴对称图形的概念求解.
【解答】解:A、不是轴对称图形,符合题意;
B、是轴对称图形,不合题意;
C、是轴对称图形,不合题意;
D、是轴对称图形,不合题意.
故选:A.
2.在直角坐标系中,点P(﹣2,3)到原点的距离是( )
A. B. C. D.2
【分析】在平面直角坐标系中找出P点,过P作PE垂直于x轴,连接OP,由P的坐标得出PE及OE的长,在直角三角形OPE中,由PE及OE的长,利用勾股定理求出OP的长,即为P到原点的距离.
【解答】解:过P作PE⊥x轴,连接OP,
∵P(﹣2,3),
∴PE=3,OE=2.
在Rt△OPE中,根据勾股定理得:OP2=PE2+OE2,
∴OP==,则点P在原点的距离为.
故选:B.
3.下列四组线段中,可以构成直角三角形的是 ( )
A.1、2、3 B.3、4、5 C.1、1、 D.6、7、8
【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个是直角三角形判定则可.如果有这种关系,这个就是直角三角形.
【解答】解:A、∵12+22≠32,∴该三角形不符合勾股定理的逆定理,故不可以构成直角三角形;
B、∵32+42=52,∴该三角形符合勾股定理的逆定理,故可以构成直角三角形;
C、∵12+12≠()2,∴该三角形不符合勾股定理的逆定理,故不可以构成直角三角形;
D、∵62+72≠82,∴该三角形不符合勾股定理的逆定理,故不可以构成直角三角形.
故选:B.
4.在?ABCD中,∠A:∠B=7:2,则∠C等于( )
A.40° B.80° C.120° D.140°
【分析】由平行四边形的性质可得∠A+∠B=180°,又有∠A:∠B=7:2,可求得∠A=140°,∴∠C=∠A=140°
【解答】解:∵?ABCD
∴∠A+∠B=180°
又∵∠A:∠B=7:2
∴∠A=140°
∵∠C=∠A
∴∠C=140°,
故选:D.
5.如图,?ABCD中,∠DAB的平分线AE交CD于E,AB=5,BC=3,则EC的长( )
A.1 B.l.5 C.2 D.3
【分析】根据平行四边形的性质得出AD=BC=3,CD=AB=5,CD∥AB,求出∠DEA=∠EAB,求出∠DEA=∠DAE,即可求出DE=AD=3,即可求出答案.
【解答】解:∵四边形ABCD是平行四边形,BC=3,AB=5,
∴AD=BC=3,CD=AB=5,CD∥AB,
∴∠DEA=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠DEA=∠DAE,
∴DE=AD=3,
∴EC=CD﹣DE=5﹣3=2,
故选:C.
6.如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD C.OA=OB D.OA=AD
【分析】根据矩形的对角线互相平分且相等,四个角都是直角对各选项分析判断利用排除法求解.
【解答】解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC=OB=OD,∠DAB=∠ABC=∠BCD=∠CDA=90°,
∴A、B、C各项结论都正确,
而OA=AD不一定成立,
故选:D.
7.平行四边形和矩形都具有的性质是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.每条对角线平分一组对角
【分析】根据平行四边形和矩形的性质即可得出结论.
【解答】解:平行四边形的性质为:对边平行且相等,对角相等,对角线互相平分;
矩形的性质为:对边平行且相等,四个角都是直角,对角线互相平分且相等;
故选:A.
8.如图,在Rt△ABC中,∠B=90°,BC=12,AB=5,则斜边上的中线BO长是( )
A.2.5 B.4 C.6 D.6.5
【分析】先利用勾股定理求出斜边AC的长,再根据直角三角形斜边上的中线等于斜边的一半即可求出BO的长.
【解答】解:∵在Rt△ABC中,∠B=90°,BC=12,AB=5,
∴AC===13,
∴斜边上的中线BO=AC=6.5.
故选:D.
9.如图,在Rt△ABC中,∠BAC=90°,点D在BC上,过D作DF⊥BC交BA的延长线于F,连接AD,CF,若∠CFE=32°,∠ADB=45°,则∠B的大小是( )
A.32° B.64° C.77° D.87°
【分析】如图,取CF的中点T,连接DT,AT.想办法证明AC=AF,推出∠CFA=45°即可解决问题.
【解答】解:如图,取CF的中点T,连接DT,AT.
∵∠BAC=90°,FD⊥BC,
∴∠CAF=∠CDF=90°,
∴AT=DT=CF,
∴TD=TC=TA,
∴∠TDA=∠TAD,∠TDC=∠TCD,
∵∠ADB=45°,
∴∠ADT+∠TDC=135°,
∴∠ATC=360°﹣2×135°=90°,
∴AT⊥CF,
∵CT=TF,
∴AC=AF,
∴∠AFC=45°,
∴∠BFD=45°﹣32°=13°,
∵∠BDF=90°,
∴∠B=90°﹣∠BFD=77°,
故选:C.
10.在矩形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD交BC于点E,∠CAE=15°,连接OE,则下面的结论:其中正确的结论有( )
①△DOC是等边三角形;
②△BOE是等腰三角形;
③BC=2AB;
④∠AOE=150°;
⑤S△AOE=S△COE.
A.2 个 B.3个 C.4 个 D.5个
【分析】判断出△ABE是等腰直角三角形,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠ACB=30°,再判断出△ABO,△DOC是等边三角形,可判断①;根据等边三角形的性质求出OB=AB,再求出OB=BE,可判断②,由直角三角形的性质可得BC=AB,可判断③,由等腰三角形性质求出∠BOE=75°,再根据∠AOE=∠AOB+∠BOE=135°,可判断④;由面积公式可得S△AOE=S△COE可判断⑤;即可求解.
【解答】解:∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠CAE=15°,
∴∠ACE=∠AEB﹣∠CAE=45°﹣15°=30°,
∴∠BAO=90°﹣30°=60°,
∵矩形ABCD中:OA=OB=OC=OD,
∴△ABO是等边三角形,△COD是等边三角形,故①正确;
∴OB=AB,∠ABO=∠AOB=60°,
∴OB=BE,
∴△BOE是等腰三角形,故②正确;
∵∠OBE=∠ABC﹣∠ABO=90°﹣60°=30°=∠ACB,
∴∠BOE=(180°﹣30°)=75°,BC=AB,故③错误;
∴∠AOE=∠AOB+∠BOE=60°+75°=135°,故④错误;
∵AO=CO,
∴S△AOE=S△COE,故⑤正确;
故选:B.
二.填空题
11.在?ABCD中,如果∠A+∠C=140°,那么∠C等于 70° .
【分析】由四边形ABCD是平行四边形,根据平行四边形的对角相等,可得:∠A=∠C,又由∠A+∠C=140°,即可求得答案.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=140°,
∴∠C=70°.
故答案为:70°.
12.平行四边形的周长等于16cm,两邻边长的比为3:1,那么这个平行四边形较长的边长为 6 cm.
【分析】利用平行四边形的对边相等,进而得出方程求出答案即可.
【解答】解:∵平行四边形的周长为16cm,相邻两边长的比为3:1,
∴设平行四边形较短边长为x,则较长边长为3x,
由题意得:3x+x=×16,
解得:x=2,
∴3x=6,
即这个平行四边形较长的边长为6cm,
故答案为:6.
13.在△ABC中,∠C=90°,∠A=45°,AC=2,斜边AB的长为 2 .
【分析】首先证明CA=CB=2,再利用勾股定理求解即可.
【解答】解:如图,
∵∠C=90°,∠A=45°,
∴∠B=90°﹣45°=45°,
∴∠A=∠B,
∴AC=CB=2,
∴AB===2.
故答案为:2.
14.如图,以直角三角形ABC的三边向外作正方形,三个正方形的面积分别为S1,S2,S3,若S1=9,S2=16,则S3= 25 .
【分析】根据勾股定理得到AB2=AC2+BC2,代入计算即可.
【解答】解:由勾股定理得,AB2=AC2+BC2,
∴S3=S1+S2=9+16=25,
故答案为:25.
15.如图,在?ABCD中,AB=,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为 3 .
【分析】由点B恰好与点C重合,可知AE垂直平分BC,根据勾股定理计算AE的长即可.
【解答】解:∵翻折后点B恰好与点C重合,
∴AE⊥BC,BE=CE,
∵BC=AD=4,
∴BE=2,
∴AE===3.
故答案为:3.
16.一个三角形的面积是12,则连接这个三角形各边中点围成的三角形的面积是 3 .
【分析】连接任意三角形两边的中点得三角形的一条中位线,且三条中位线所围成的三角形与原来三角形相似,相似比为1:2,则面积的比为1:4,从而根据原三角形的面积求得小三角形的面积即可.
【解答】解:三角形的中位线所围成的三角形与原来三角形相似,
∵中位线:第三边=1:2,
∴三条中位线所围成的三角形的面积:原来三角形的面积=1:4,
∵三角形的面积是12,
∴连接这个三角形各边中点围成的三角形的面积是3,
故答案为:3.
17.一架长为10m的梯子,斜靠在竖直的墙上,这时梯子的底端与墙的距离为6m,如果梯子顶端沿墙下滑2m,那么梯子底端将滑动 2 m.
【分析】首先在Rt△ABO中利用勾股定理计算出AO的长,在Rt△COD中计算出DO的长,进而可得BD的长.
【解答】解:在Rt△ABO中:AO===8(米),
∵梯子的顶端下滑了2m,
∴AC=2米,
∴CO=6米,
在Rt△COD中:DO===8(米),
∴BD=DO﹣BO=8﹣6=2(米),
故答案为:2.
18.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH= .
【分析】先根据菱形的性质得OA=OC=4,OB=OD=3,AC⊥BD,再利用勾股定理计算出AB=5,然后根据菱形的面积公式得到?AC?BD=DH?AB,再解关于DH的方程即可.
【解答】解:∵四边形ABCD是菱形,
∴OA=OC=4,OB=OD=3,AC⊥BD,
在Rt△AOB中,AB==5,
∵S菱形ABCD=?AC?BD,
S菱形ABCD=DH?AB,
∴DH?5=?6?8,
∴DH=.
故答案为.
19.在?ABCD中,AB=5,AC=,BC边上的高为4,则BC= 5或1 .
【分析】分两种情况,根据题意分别画出图形,BC边上的高在平行四边形的内部和外部,进而利用勾股定理求出即可.
【解答】解:分两种情况;
①如图1所示:
在?ABCD中,BC边上的高AE为4,AB=5,AC=2,
∴EC===2,
BE===3,
∴BC=BE+CE=3+2=5;
②如图2所示:
同①得:EC=2,AB=CD=5,BE=3,
∴BC=BE﹣EC=3﹣2=1;
综上所述,BC的长为5或1,
故答案为:5或1.
20.在矩形ABCD中,点E、F分别在AB、AD上,CD=9,CE=20,∠EFB=2∠AFE=2∠BCE,则线段AF的长为 .
【分析】设BF与CE的交点为G,取CE的中点H,连接BH,设∠EFB=2∠AFE=2∠BCE=2α,由矩形的性质及直角三角形的斜边中线性质得出BH=CH=EH=10,∠HBC=∠HCB=α,再判定EF∥BH、△EFG和△BGH均为等腰三角形,最后由勾股定理求得AF即可.
【解答】解:设BF与CE的交点为G,取CE的中点H,连接BH,如图所示:
设∠EFB=2∠AFE=2∠BCE=2α,则∠AFB=3α,
在矩形ABCD中有AD∥BC,∠A=∠ABC=90°,
∴△BCE为直角三角形,
∵点H为斜边CE的中点,CE=20,
∴BH=CH=EH=10,
∴∠HBC=∠HCB=α,
∵AD∥BC,
∴∠AFB=∠FBC=3α,
∴∠GHB=3α﹣α=2α=∠EFB,
∴EF∥BH,
∴∠FEG=∠GHB
=∠HBC+∠HCB
=2α
=∠EFB
=∠GBH,
∴△EFG和△BGH均为等腰三角形,
∴BF=EH=10,
在矩形ABCD中,AB=CD=9,
由勾股定理得:
AF=
=
=.
故答案为:.
三.解答题(共7小题)
21.先化简,再求值:÷﹣,其中x=﹣2.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再将x的值代入计算可得.
【解答】解:原式=?﹣
=﹣
=,
当x=﹣2时,
原式===.
22.如图,正方形网格中的每个小正方形边长都是1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画图:
(1)在图①中画一个面积为18的正方形;
(2)在图②中画一个面积为12的菱形,并直接写出所画菱形的周长.
【分析】(1)作出边长为3的正方形即可.
(2)作出对角线为4,6的菱形即可.
【解答】解:(1)如图,正方形ABCD即为所求.
(2)如图,菱形EFGH即为所求.
23.如图所示的一块地ABCD,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m,求这块地的面积.
【分析】连接AC,利用勾股定理可以得出三角形ACD和ABC是直角三角形,△ABC的面积减去△ACD的面积就是所求的面积.
【解答】解:连接AC,
∵∠ADC=90°,AD=4,CD=3,
∴AC2=AD2+CD2=42+32=25,
又∵AC>0,
∴AC=5,
又∵BC=12,AB=13,
∴AC2+BC2=52+122=169,
又∵AB2=169,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴S四边形ABCD=S△ABC﹣S△ADC=30﹣6=24m2.
24.在△ABC中,AD⊥BC于点D,点E为AC边的中点,过点A作AF∥BC,交DE的延长线于点F,连接CF.
(1)如图1,求证:四边形ADCF是矩形;
(2)如图2,当AB=AC时,取AB的中点G,连接DG、EG,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形ADCF).
【分析】(1)由△AEF≌△CED,推出EF=DE,又AE=EC,推出四边形ADCF是平行四边形,只要证明∠ADC=90°,即可推出四边形ADCF是矩形.
(2)四边形ABDF、四边形AGEF、四边形GBDE、四边形AGDE、四边形GDCE都是平行四边形.
【解答】(1)证明:∵AF∥BC,
∴∠AFE=∠EDC,
∵E是AC中点,
∴AE=EC,
在△AEF和△CED中,
,
∴△AEF≌△CED,
∴EF=DE,∵AE=EC,
∴四边形ADCF是平行四边形,
∵AD⊥BC,
∴∠ADC=90°,
∴四边形ADCF是矩形.
(2)∵线段DG、线段GE、线段DE都是△ABC的中位线,又AF∥BC,
∴AB∥DE,DG∥AC,EG∥BC,
∴四边形ABDF、四边形AGEF、四边形GBDE、四边形AGDE、四边形GDCE都是平行四边形.
25.植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
【分析】(1)设B树苗的单价为x元,则A树苗的单价为y元.则由等量关系列出方程组解答即可;
(2)设购买A种树苗a棵,则B种树苗为(30﹣a)棵,然后根据总费用和两种树的棵数关系列出不等式解答即可.
【解答】解:设B树苗的单价为x元,则A树苗的单价为y元,可得:,
解得:,
答:B树苗的单价为300元,A树苗的单价为200元;
(2)设购买A种树苗a棵,则B种树苗为(30﹣a)棵,
可得:200a+300(30﹣a)≤8000,
解得:a≥10,
答:A种树苗至少需购进10棵.
26.如图,四边形ABCD是正方形,点E在边CD的延长线上,CF⊥AE于点F,交AD于点G.
(1)求证:AE=CG;
(2)点H为BC延长线上一点,连接EH,∠HEF=∠DGF,求证:∠CEH=2∠DAE;
(3)在(2)的条件下,AB=4,CH=,求线段CG的长度.
【分析】(1)证明△ADE≌△CDG(AAS),即可求解;
(2)在△AFG中,∠DGF=∠DAE+∠AFG=90°+∠DAE,而∠HEF=∠HEC+∠AED=∠HEC+∠FED=∠HEC+90°﹣∠DAE,即可求解;
(3)在△CEH中,tan∠CEH====tan∠NAK=tan2α,在△AEK中,S△AKE=×AD×EK=×NK×AE,即4×2x=NK×,求出NK,则AN=AE﹣NE=﹣EKcos∠AEK=﹣2x?cos∠AED,则tan∠NAK===,即可求解.
【解答】解:(1)∵四边形ABCD为正方形,
故AD=CD,
∵∠GCD=∠ADC﹣∠DGC=90°﹣∠DGC,
∵∠EAD=∠ADE﹣∠FGA=90°﹣∠FGA,
而∠DGC=∠FGA,
∴∠DCG=∠EAD,
∵AD=CD,∠ADE=∠CDG=90°,
∴△ADE≌△CDG(AAS),
∴AE=CG;
(2)在△AFG中,∠DGF=∠DAE+∠AFG=90°+∠DAE,
而∠HEF=∠HEC+∠AED=∠HEC+∠FED=∠HEC+90°﹣∠DAE,
∵∠HEF=∠DGF,
则90°+∠DAE=∠HEC+90°﹣∠DAE,
∴∠CEH=2∠DAE;
(3)如图,在CD上取DK=DE,则∠EAK=2∠EAD=∠CEH,
过点K作KN⊥AE于点N,
设DE=DK=x,∠EAK=2∠EAD=∠CEH=2α,则∠EAD=α,
在△CEH中,tan∠CEH====tan∠NAK=tan2α,
在Rt△ADE中,tan∠EAD==,则tan∠AED=,则cos∠AED=,
而AE=,
在△AEK中,S△AKE=×AD×EK=×NK×AE,即4×2x=NK×,解得NK=,
则AN=AE﹣NE=﹣EKcos∠AEK=﹣2x?cos∠AED,
则tan∠NAK===,解得x=﹣4(舍去)或1,
故x=1,则AE==,
由(1)知,CG=AE=.
27.如图,在平面直角坐标系中,正方形ABCD的边BC落在x轴上,连接AC,AC=4,OC=1.
(1)求点A的坐标;
(2)点P为线段AB上一动点,连接CP,点E为CP的中点,设点P的纵坐标为t,△PEA的面积为S,求S与t的关系式;
(3)在(2)的条件下,在x轴的负半轴上取点F(﹣5,0),连接DF,点Q为线段DF上一点,连接EQ,且EQ=AE,当△PEA的面积为3时,求线段DQ的长度.
【分析】(1)由正方形的性质得AB=BC=CD=AD=AC=4,∠ABC=90°,则OB=BC﹣OC=3,得A(3,4);
(2)由题意得P(3,t),AP=4﹣t,则E(1,),再由三角形面积公式求解即可;
(3)由题意得4﹣t=3,则t=1,得P(3,1),E(1,),由勾股定理得AE2=,再由待定系数法求出直线DF的解析式为y=x+5,设Q(x,x+5),如何由勾股定理得EQ2=(1﹣x)2+(x+5﹣)2,则(1﹣x)2+(x+5﹣)2=16,解得x=﹣1或x=﹣,即可解决问题.
【解答】解:(1)∵四边形ABCD是正方形,AC=4,
∴AB=BC=CD=AD=AC=4,∠ABC=90°,
∴OB=BC﹣OC=4﹣1=3,
∴A(3,4);
(2)∵点P为线段AB上一动点,点P的纵坐标为t,
∴P(3,t),AP=4﹣t,
∵OC=1,
∴C(﹣1,0),
∵点E为CP的中点,
∴E(1,),
∴△PEA的面积为S=×(4﹣t)×(3﹣1)=4﹣t,
即S与t的关系式为S=4﹣t;
(3)当△PEA的面积为3时,4﹣t=3,
∴t=1,
∴P(3,1),E(1,),
∴AE2=(3﹣1)2+(4﹣)2=,
由(1)得:D(﹣1,4),
设直线DF的解析式为y=kx+b,
把D(﹣1,4),F(﹣5,0)代入得:,
解得:,
∴直线DF的解析式为y=x+5,
设Q(x,x+5),
∵EQ2=(1﹣x)2+(x+5﹣)2,EQ=AE,
∴(1﹣x)2+(x+5﹣)2=16,
整理得:2x2+7x+5=0,
解得:x=﹣1或x=﹣,
即点Q的坐标为(﹣1,4)或(﹣,),
当点Q坐标为(﹣1,4)时,DQ=0;
当点Q坐标为(﹣,)时,DQ==;
综上所述,当△PEA的面积为3时,线段DQ的长度为0或.
一、选择题(每小题3分,共计30分)
1.下面选项中的四边形不是轴对称图形的是( )
A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
2.在直角坐标系中,点P(﹣2,3)到原点的距离是( )
A. B. C. D.2
3.下列四组线段中,可以构成直角三角形的是 ( )
A.1、2、3 B.3、4、5 C.1、1、 D.6、7、8
4.在?ABCD中,∠A:∠B=7:2,则∠C等于( )
A.40° B.80° C.120° D.140°
5.如图,?ABCD中,∠DAB的平分线AE交CD于E,AB=5,BC=3,则EC的长( )
A.1 B.l.5 C.2 D.3
6.如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD C.OA=OB D.OA=AD
7.平行四边形和矩形都具有的性质是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.每条对角线平分一组对角
8.如图,在Rt△ABC中,∠B=90°,BC=12,AB=5,则斜边上的中线BO长是( )
A.2.5 B.4 C.6 D.6.5
9.如图,在Rt△ABC中,∠BAC=90°,点D在BC上,过D作DF⊥BC交BA的延长线于F,连接AD,CF,若∠CFE=32°,∠ADB=45°,则∠B的大小是( )
A.32° B.64° C.77° D.87°
10.在矩形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD交BC于点E,∠CAE=15°,连接OE,则下面的结论:其中正确的结论有( )
①△DOC是等边三角形;
②△BOE是等腰三角形;
③BC=2AB;
④∠AOE=150°;
⑤S△AOE=S△COE.
A.2 个 B.3个 C.4 个 D.5个
二、填空题(每小题3分,共计30分)
11.在?ABCD中,如果∠A+∠C=140°,那么∠C等于 .
12.平行四边形的周长等于16cm,两邻边长的比为3:1,那么这个平行四边形较长的边长为 cm.
13.在△ABC中,∠C=90°,∠A=45°,AC=2,斜边AB的长为 .
14.如图,以直角三角形ABC的三边向外作正方形,三个正方形的面积分别为S1,S2,S3,若S1=9,S2=16,则S3= .
15.如图,在?ABCD中,AB=,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为 .
16.一个三角形的面积是12,则连接这个三角形各边中点围成的三角形的面积是 .
17.一架长为10m的梯子,斜靠在竖直的墙上,这时梯子的底端与墙的距离为6m,如果梯子顶端沿墙下滑2m,那么梯子底端将滑动 m.
18.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH= .
19.在?ABCD中,AB=5,AC=,BC边上的高为4,则BC= .
20.在矩形ABCD中,点E、F分别在AB、AD上,CD=9,CE=20,∠EFB=2∠AFE=2∠BCE,则线段AF的长为 .
三、解答题(其中21~22题各7分,23~24题各8分,25~27题各10分,共计60分)21.先化简,再求值:÷﹣,其中x=﹣2.
22.如图,正方形网格中的每个小正方形边长都是1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画图:
(1)在图①中画一个面积为18的正方形;
(2)在图②中画一个面积为12的菱形,并直接写出所画菱形的周长.
23.如图所示的一块地ABCD,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m,求这块地的面积.
24.在△ABC中,AD⊥BC于点D,点E为AC边的中点,过点A作AF∥BC,交DE的延长线于点F,连接CF.
(1)如图1,求证:四边形ADCF是矩形;
(2)如图2,当AB=AC时,取AB的中点G,连接DG、EG,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形ADCF).
25.植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
26.如图,四边形ABCD是正方形,点E在边CD的延长线上,CF⊥AE于点F,交AD于点G.
(1)求证:AE=CG;
(2)点H为BC延长线上一点,连接EH,∠HEF=∠DGF,求证:∠CEH=2∠DAE;
(3)在(2)的条件下,AB=4,CH=,求线段CG的长度.
27.如图,在平面直角坐标系中,正方形ABCD的边BC落在x轴上,连接AC,AC=4,OC=1.
(1)求点A的坐标;
(2)点P为线段AB上一动点,连接CP,点E为CP的中点,设点P的纵坐标为t,△PEA的面积为S,求S与t的关系式;
(3)在(2)的条件下,在x轴的负半轴上取点F(﹣5,0),连接DF,点Q为线段DF上一点,连接EQ,且EQ=AE,当△PEA的面积为3时,求线段DQ的长度.
2019-2020学年黑龙江省哈尔滨四十七中八年级(下)月考数学试卷(3月份)(五四学制)
参考答案与试题解析
一.选择题(共10小题)
1.下面选项中的四边形不是轴对称图形的是( )
A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
【分析】根据轴对称图形的概念求解.
【解答】解:A、不是轴对称图形,符合题意;
B、是轴对称图形,不合题意;
C、是轴对称图形,不合题意;
D、是轴对称图形,不合题意.
故选:A.
2.在直角坐标系中,点P(﹣2,3)到原点的距离是( )
A. B. C. D.2
【分析】在平面直角坐标系中找出P点,过P作PE垂直于x轴,连接OP,由P的坐标得出PE及OE的长,在直角三角形OPE中,由PE及OE的长,利用勾股定理求出OP的长,即为P到原点的距离.
【解答】解:过P作PE⊥x轴,连接OP,
∵P(﹣2,3),
∴PE=3,OE=2.
在Rt△OPE中,根据勾股定理得:OP2=PE2+OE2,
∴OP==,则点P在原点的距离为.
故选:B.
3.下列四组线段中,可以构成直角三角形的是 ( )
A.1、2、3 B.3、4、5 C.1、1、 D.6、7、8
【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个是直角三角形判定则可.如果有这种关系,这个就是直角三角形.
【解答】解:A、∵12+22≠32,∴该三角形不符合勾股定理的逆定理,故不可以构成直角三角形;
B、∵32+42=52,∴该三角形符合勾股定理的逆定理,故可以构成直角三角形;
C、∵12+12≠()2,∴该三角形不符合勾股定理的逆定理,故不可以构成直角三角形;
D、∵62+72≠82,∴该三角形不符合勾股定理的逆定理,故不可以构成直角三角形.
故选:B.
4.在?ABCD中,∠A:∠B=7:2,则∠C等于( )
A.40° B.80° C.120° D.140°
【分析】由平行四边形的性质可得∠A+∠B=180°,又有∠A:∠B=7:2,可求得∠A=140°,∴∠C=∠A=140°
【解答】解:∵?ABCD
∴∠A+∠B=180°
又∵∠A:∠B=7:2
∴∠A=140°
∵∠C=∠A
∴∠C=140°,
故选:D.
5.如图,?ABCD中,∠DAB的平分线AE交CD于E,AB=5,BC=3,则EC的长( )
A.1 B.l.5 C.2 D.3
【分析】根据平行四边形的性质得出AD=BC=3,CD=AB=5,CD∥AB,求出∠DEA=∠EAB,求出∠DEA=∠DAE,即可求出DE=AD=3,即可求出答案.
【解答】解:∵四边形ABCD是平行四边形,BC=3,AB=5,
∴AD=BC=3,CD=AB=5,CD∥AB,
∴∠DEA=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠DEA=∠DAE,
∴DE=AD=3,
∴EC=CD﹣DE=5﹣3=2,
故选:C.
6.如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD C.OA=OB D.OA=AD
【分析】根据矩形的对角线互相平分且相等,四个角都是直角对各选项分析判断利用排除法求解.
【解答】解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC=OB=OD,∠DAB=∠ABC=∠BCD=∠CDA=90°,
∴A、B、C各项结论都正确,
而OA=AD不一定成立,
故选:D.
7.平行四边形和矩形都具有的性质是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.每条对角线平分一组对角
【分析】根据平行四边形和矩形的性质即可得出结论.
【解答】解:平行四边形的性质为:对边平行且相等,对角相等,对角线互相平分;
矩形的性质为:对边平行且相等,四个角都是直角,对角线互相平分且相等;
故选:A.
8.如图,在Rt△ABC中,∠B=90°,BC=12,AB=5,则斜边上的中线BO长是( )
A.2.5 B.4 C.6 D.6.5
【分析】先利用勾股定理求出斜边AC的长,再根据直角三角形斜边上的中线等于斜边的一半即可求出BO的长.
【解答】解:∵在Rt△ABC中,∠B=90°,BC=12,AB=5,
∴AC===13,
∴斜边上的中线BO=AC=6.5.
故选:D.
9.如图,在Rt△ABC中,∠BAC=90°,点D在BC上,过D作DF⊥BC交BA的延长线于F,连接AD,CF,若∠CFE=32°,∠ADB=45°,则∠B的大小是( )
A.32° B.64° C.77° D.87°
【分析】如图,取CF的中点T,连接DT,AT.想办法证明AC=AF,推出∠CFA=45°即可解决问题.
【解答】解:如图,取CF的中点T,连接DT,AT.
∵∠BAC=90°,FD⊥BC,
∴∠CAF=∠CDF=90°,
∴AT=DT=CF,
∴TD=TC=TA,
∴∠TDA=∠TAD,∠TDC=∠TCD,
∵∠ADB=45°,
∴∠ADT+∠TDC=135°,
∴∠ATC=360°﹣2×135°=90°,
∴AT⊥CF,
∵CT=TF,
∴AC=AF,
∴∠AFC=45°,
∴∠BFD=45°﹣32°=13°,
∵∠BDF=90°,
∴∠B=90°﹣∠BFD=77°,
故选:C.
10.在矩形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD交BC于点E,∠CAE=15°,连接OE,则下面的结论:其中正确的结论有( )
①△DOC是等边三角形;
②△BOE是等腰三角形;
③BC=2AB;
④∠AOE=150°;
⑤S△AOE=S△COE.
A.2 个 B.3个 C.4 个 D.5个
【分析】判断出△ABE是等腰直角三角形,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠ACB=30°,再判断出△ABO,△DOC是等边三角形,可判断①;根据等边三角形的性质求出OB=AB,再求出OB=BE,可判断②,由直角三角形的性质可得BC=AB,可判断③,由等腰三角形性质求出∠BOE=75°,再根据∠AOE=∠AOB+∠BOE=135°,可判断④;由面积公式可得S△AOE=S△COE可判断⑤;即可求解.
【解答】解:∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠CAE=15°,
∴∠ACE=∠AEB﹣∠CAE=45°﹣15°=30°,
∴∠BAO=90°﹣30°=60°,
∵矩形ABCD中:OA=OB=OC=OD,
∴△ABO是等边三角形,△COD是等边三角形,故①正确;
∴OB=AB,∠ABO=∠AOB=60°,
∴OB=BE,
∴△BOE是等腰三角形,故②正确;
∵∠OBE=∠ABC﹣∠ABO=90°﹣60°=30°=∠ACB,
∴∠BOE=(180°﹣30°)=75°,BC=AB,故③错误;
∴∠AOE=∠AOB+∠BOE=60°+75°=135°,故④错误;
∵AO=CO,
∴S△AOE=S△COE,故⑤正确;
故选:B.
二.填空题
11.在?ABCD中,如果∠A+∠C=140°,那么∠C等于 70° .
【分析】由四边形ABCD是平行四边形,根据平行四边形的对角相等,可得:∠A=∠C,又由∠A+∠C=140°,即可求得答案.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A+∠C=140°,
∴∠C=70°.
故答案为:70°.
12.平行四边形的周长等于16cm,两邻边长的比为3:1,那么这个平行四边形较长的边长为 6 cm.
【分析】利用平行四边形的对边相等,进而得出方程求出答案即可.
【解答】解:∵平行四边形的周长为16cm,相邻两边长的比为3:1,
∴设平行四边形较短边长为x,则较长边长为3x,
由题意得:3x+x=×16,
解得:x=2,
∴3x=6,
即这个平行四边形较长的边长为6cm,
故答案为:6.
13.在△ABC中,∠C=90°,∠A=45°,AC=2,斜边AB的长为 2 .
【分析】首先证明CA=CB=2,再利用勾股定理求解即可.
【解答】解:如图,
∵∠C=90°,∠A=45°,
∴∠B=90°﹣45°=45°,
∴∠A=∠B,
∴AC=CB=2,
∴AB===2.
故答案为:2.
14.如图,以直角三角形ABC的三边向外作正方形,三个正方形的面积分别为S1,S2,S3,若S1=9,S2=16,则S3= 25 .
【分析】根据勾股定理得到AB2=AC2+BC2,代入计算即可.
【解答】解:由勾股定理得,AB2=AC2+BC2,
∴S3=S1+S2=9+16=25,
故答案为:25.
15.如图,在?ABCD中,AB=,AD=4,将?ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为 3 .
【分析】由点B恰好与点C重合,可知AE垂直平分BC,根据勾股定理计算AE的长即可.
【解答】解:∵翻折后点B恰好与点C重合,
∴AE⊥BC,BE=CE,
∵BC=AD=4,
∴BE=2,
∴AE===3.
故答案为:3.
16.一个三角形的面积是12,则连接这个三角形各边中点围成的三角形的面积是 3 .
【分析】连接任意三角形两边的中点得三角形的一条中位线,且三条中位线所围成的三角形与原来三角形相似,相似比为1:2,则面积的比为1:4,从而根据原三角形的面积求得小三角形的面积即可.
【解答】解:三角形的中位线所围成的三角形与原来三角形相似,
∵中位线:第三边=1:2,
∴三条中位线所围成的三角形的面积:原来三角形的面积=1:4,
∵三角形的面积是12,
∴连接这个三角形各边中点围成的三角形的面积是3,
故答案为:3.
17.一架长为10m的梯子,斜靠在竖直的墙上,这时梯子的底端与墙的距离为6m,如果梯子顶端沿墙下滑2m,那么梯子底端将滑动 2 m.
【分析】首先在Rt△ABO中利用勾股定理计算出AO的长,在Rt△COD中计算出DO的长,进而可得BD的长.
【解答】解:在Rt△ABO中:AO===8(米),
∵梯子的顶端下滑了2m,
∴AC=2米,
∴CO=6米,
在Rt△COD中:DO===8(米),
∴BD=DO﹣BO=8﹣6=2(米),
故答案为:2.
18.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH= .
【分析】先根据菱形的性质得OA=OC=4,OB=OD=3,AC⊥BD,再利用勾股定理计算出AB=5,然后根据菱形的面积公式得到?AC?BD=DH?AB,再解关于DH的方程即可.
【解答】解:∵四边形ABCD是菱形,
∴OA=OC=4,OB=OD=3,AC⊥BD,
在Rt△AOB中,AB==5,
∵S菱形ABCD=?AC?BD,
S菱形ABCD=DH?AB,
∴DH?5=?6?8,
∴DH=.
故答案为.
19.在?ABCD中,AB=5,AC=,BC边上的高为4,则BC= 5或1 .
【分析】分两种情况,根据题意分别画出图形,BC边上的高在平行四边形的内部和外部,进而利用勾股定理求出即可.
【解答】解:分两种情况;
①如图1所示:
在?ABCD中,BC边上的高AE为4,AB=5,AC=2,
∴EC===2,
BE===3,
∴BC=BE+CE=3+2=5;
②如图2所示:
同①得:EC=2,AB=CD=5,BE=3,
∴BC=BE﹣EC=3﹣2=1;
综上所述,BC的长为5或1,
故答案为:5或1.
20.在矩形ABCD中,点E、F分别在AB、AD上,CD=9,CE=20,∠EFB=2∠AFE=2∠BCE,则线段AF的长为 .
【分析】设BF与CE的交点为G,取CE的中点H,连接BH,设∠EFB=2∠AFE=2∠BCE=2α,由矩形的性质及直角三角形的斜边中线性质得出BH=CH=EH=10,∠HBC=∠HCB=α,再判定EF∥BH、△EFG和△BGH均为等腰三角形,最后由勾股定理求得AF即可.
【解答】解:设BF与CE的交点为G,取CE的中点H,连接BH,如图所示:
设∠EFB=2∠AFE=2∠BCE=2α,则∠AFB=3α,
在矩形ABCD中有AD∥BC,∠A=∠ABC=90°,
∴△BCE为直角三角形,
∵点H为斜边CE的中点,CE=20,
∴BH=CH=EH=10,
∴∠HBC=∠HCB=α,
∵AD∥BC,
∴∠AFB=∠FBC=3α,
∴∠GHB=3α﹣α=2α=∠EFB,
∴EF∥BH,
∴∠FEG=∠GHB
=∠HBC+∠HCB
=2α
=∠EFB
=∠GBH,
∴△EFG和△BGH均为等腰三角形,
∴BF=EH=10,
在矩形ABCD中,AB=CD=9,
由勾股定理得:
AF=
=
=.
故答案为:.
三.解答题(共7小题)
21.先化简,再求值:÷﹣,其中x=﹣2.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再将x的值代入计算可得.
【解答】解:原式=?﹣
=﹣
=,
当x=﹣2时,
原式===.
22.如图,正方形网格中的每个小正方形边长都是1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画图:
(1)在图①中画一个面积为18的正方形;
(2)在图②中画一个面积为12的菱形,并直接写出所画菱形的周长.
【分析】(1)作出边长为3的正方形即可.
(2)作出对角线为4,6的菱形即可.
【解答】解:(1)如图,正方形ABCD即为所求.
(2)如图,菱形EFGH即为所求.
23.如图所示的一块地ABCD,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m,求这块地的面积.
【分析】连接AC,利用勾股定理可以得出三角形ACD和ABC是直角三角形,△ABC的面积减去△ACD的面积就是所求的面积.
【解答】解:连接AC,
∵∠ADC=90°,AD=4,CD=3,
∴AC2=AD2+CD2=42+32=25,
又∵AC>0,
∴AC=5,
又∵BC=12,AB=13,
∴AC2+BC2=52+122=169,
又∵AB2=169,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴S四边形ABCD=S△ABC﹣S△ADC=30﹣6=24m2.
24.在△ABC中,AD⊥BC于点D,点E为AC边的中点,过点A作AF∥BC,交DE的延长线于点F,连接CF.
(1)如图1,求证:四边形ADCF是矩形;
(2)如图2,当AB=AC时,取AB的中点G,连接DG、EG,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形ADCF).
【分析】(1)由△AEF≌△CED,推出EF=DE,又AE=EC,推出四边形ADCF是平行四边形,只要证明∠ADC=90°,即可推出四边形ADCF是矩形.
(2)四边形ABDF、四边形AGEF、四边形GBDE、四边形AGDE、四边形GDCE都是平行四边形.
【解答】(1)证明:∵AF∥BC,
∴∠AFE=∠EDC,
∵E是AC中点,
∴AE=EC,
在△AEF和△CED中,
,
∴△AEF≌△CED,
∴EF=DE,∵AE=EC,
∴四边形ADCF是平行四边形,
∵AD⊥BC,
∴∠ADC=90°,
∴四边形ADCF是矩形.
(2)∵线段DG、线段GE、线段DE都是△ABC的中位线,又AF∥BC,
∴AB∥DE,DG∥AC,EG∥BC,
∴四边形ABDF、四边形AGEF、四边形GBDE、四边形AGDE、四边形GDCE都是平行四边形.
25.植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
【分析】(1)设B树苗的单价为x元,则A树苗的单价为y元.则由等量关系列出方程组解答即可;
(2)设购买A种树苗a棵,则B种树苗为(30﹣a)棵,然后根据总费用和两种树的棵数关系列出不等式解答即可.
【解答】解:设B树苗的单价为x元,则A树苗的单价为y元,可得:,
解得:,
答:B树苗的单价为300元,A树苗的单价为200元;
(2)设购买A种树苗a棵,则B种树苗为(30﹣a)棵,
可得:200a+300(30﹣a)≤8000,
解得:a≥10,
答:A种树苗至少需购进10棵.
26.如图,四边形ABCD是正方形,点E在边CD的延长线上,CF⊥AE于点F,交AD于点G.
(1)求证:AE=CG;
(2)点H为BC延长线上一点,连接EH,∠HEF=∠DGF,求证:∠CEH=2∠DAE;
(3)在(2)的条件下,AB=4,CH=,求线段CG的长度.
【分析】(1)证明△ADE≌△CDG(AAS),即可求解;
(2)在△AFG中,∠DGF=∠DAE+∠AFG=90°+∠DAE,而∠HEF=∠HEC+∠AED=∠HEC+∠FED=∠HEC+90°﹣∠DAE,即可求解;
(3)在△CEH中,tan∠CEH====tan∠NAK=tan2α,在△AEK中,S△AKE=×AD×EK=×NK×AE,即4×2x=NK×,求出NK,则AN=AE﹣NE=﹣EKcos∠AEK=﹣2x?cos∠AED,则tan∠NAK===,即可求解.
【解答】解:(1)∵四边形ABCD为正方形,
故AD=CD,
∵∠GCD=∠ADC﹣∠DGC=90°﹣∠DGC,
∵∠EAD=∠ADE﹣∠FGA=90°﹣∠FGA,
而∠DGC=∠FGA,
∴∠DCG=∠EAD,
∵AD=CD,∠ADE=∠CDG=90°,
∴△ADE≌△CDG(AAS),
∴AE=CG;
(2)在△AFG中,∠DGF=∠DAE+∠AFG=90°+∠DAE,
而∠HEF=∠HEC+∠AED=∠HEC+∠FED=∠HEC+90°﹣∠DAE,
∵∠HEF=∠DGF,
则90°+∠DAE=∠HEC+90°﹣∠DAE,
∴∠CEH=2∠DAE;
(3)如图,在CD上取DK=DE,则∠EAK=2∠EAD=∠CEH,
过点K作KN⊥AE于点N,
设DE=DK=x,∠EAK=2∠EAD=∠CEH=2α,则∠EAD=α,
在△CEH中,tan∠CEH====tan∠NAK=tan2α,
在Rt△ADE中,tan∠EAD==,则tan∠AED=,则cos∠AED=,
而AE=,
在△AEK中,S△AKE=×AD×EK=×NK×AE,即4×2x=NK×,解得NK=,
则AN=AE﹣NE=﹣EKcos∠AEK=﹣2x?cos∠AED,
则tan∠NAK===,解得x=﹣4(舍去)或1,
故x=1,则AE==,
由(1)知,CG=AE=.
27.如图,在平面直角坐标系中,正方形ABCD的边BC落在x轴上,连接AC,AC=4,OC=1.
(1)求点A的坐标;
(2)点P为线段AB上一动点,连接CP,点E为CP的中点,设点P的纵坐标为t,△PEA的面积为S,求S与t的关系式;
(3)在(2)的条件下,在x轴的负半轴上取点F(﹣5,0),连接DF,点Q为线段DF上一点,连接EQ,且EQ=AE,当△PEA的面积为3时,求线段DQ的长度.
【分析】(1)由正方形的性质得AB=BC=CD=AD=AC=4,∠ABC=90°,则OB=BC﹣OC=3,得A(3,4);
(2)由题意得P(3,t),AP=4﹣t,则E(1,),再由三角形面积公式求解即可;
(3)由题意得4﹣t=3,则t=1,得P(3,1),E(1,),由勾股定理得AE2=,再由待定系数法求出直线DF的解析式为y=x+5,设Q(x,x+5),如何由勾股定理得EQ2=(1﹣x)2+(x+5﹣)2,则(1﹣x)2+(x+5﹣)2=16,解得x=﹣1或x=﹣,即可解决问题.
【解答】解:(1)∵四边形ABCD是正方形,AC=4,
∴AB=BC=CD=AD=AC=4,∠ABC=90°,
∴OB=BC﹣OC=4﹣1=3,
∴A(3,4);
(2)∵点P为线段AB上一动点,点P的纵坐标为t,
∴P(3,t),AP=4﹣t,
∵OC=1,
∴C(﹣1,0),
∵点E为CP的中点,
∴E(1,),
∴△PEA的面积为S=×(4﹣t)×(3﹣1)=4﹣t,
即S与t的关系式为S=4﹣t;
(3)当△PEA的面积为3时,4﹣t=3,
∴t=1,
∴P(3,1),E(1,),
∴AE2=(3﹣1)2+(4﹣)2=,
由(1)得:D(﹣1,4),
设直线DF的解析式为y=kx+b,
把D(﹣1,4),F(﹣5,0)代入得:,
解得:,
∴直线DF的解析式为y=x+5,
设Q(x,x+5),
∵EQ2=(1﹣x)2+(x+5﹣)2,EQ=AE,
∴(1﹣x)2+(x+5﹣)2=16,
整理得:2x2+7x+5=0,
解得:x=﹣1或x=﹣,
即点Q的坐标为(﹣1,4)或(﹣,),
当点Q坐标为(﹣1,4)时,DQ=0;
当点Q坐标为(﹣,)时,DQ==;
综上所述,当△PEA的面积为3时,线段DQ的长度为0或.
同课章节目录
