9.1.2 不等式的性质 课件 (57张)
文档属性
| 名称 | 9.1.2 不等式的性质 课件 (57张) |  | |
| 格式 | ppt | ||
| 文件大小 | 958.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-22 22:51:42 | ||
图片预览











文档简介
(共57张PPT)
第九章
9.1.2
不等式的性质
人教版数学七年级下册
1.经历通过类比、猜测、验证发现不等式基本性质的探索过程,初步体会不等式与等式的异同。
2.掌握不等式的基本性质,并能初步运用不等式的基本性质将比较简单的不等式转化为“x>a”或“x<a”的形式。
学习目标
1
知识点
不等式的性质1
我们知道,等式两边加或减同一个数(或式子),
乘或除以同一个数(除数不为0),结果仍相等.
不等
式是否也有类似的性质呢?
合作探究
如果在不等式的两边都加或都减同一个整式,
那么结果会怎样?请举几例试一试,并与同伴交流.
思考
用“>”或“<”填空,并总结其中的规律:
(1)
5>3,
5+2
3+2,
5-2
3-2;
(2)
1<3,-1
+
2
3
+
2,
-1-3
3
–
3.
不等式的性质1
不等式两边加(或减)同一个数(或
式子)
,不等号的方向不变.
如果a>b,那么a±c>b±c.
新知小结
从变形来看,是利用了不等式的性质1.
(1)根据不等式性质1,不等式两边同时减去6;
(2)根据不等式性质1,不等式两边同时减去6x.
分析:
例1
指出下列不等式是如何变形的,并说明其变形的依据.
(1)若6+y>-7,则y>-13;
(2)若7x<6x+3,则x<3.
解:
合作探究
判断某个不等式变形的根据,
一看不等号的方向是不是改变,
二看式子的变化情况.
新知小结
1
已知a<b,用“>”或“<”填空:
(1)a+2________b+2;
(2)a-3________b-3;
(3)a+c________b+c;
(4)a-b________0.
<
<
<
<
巩固新知
2
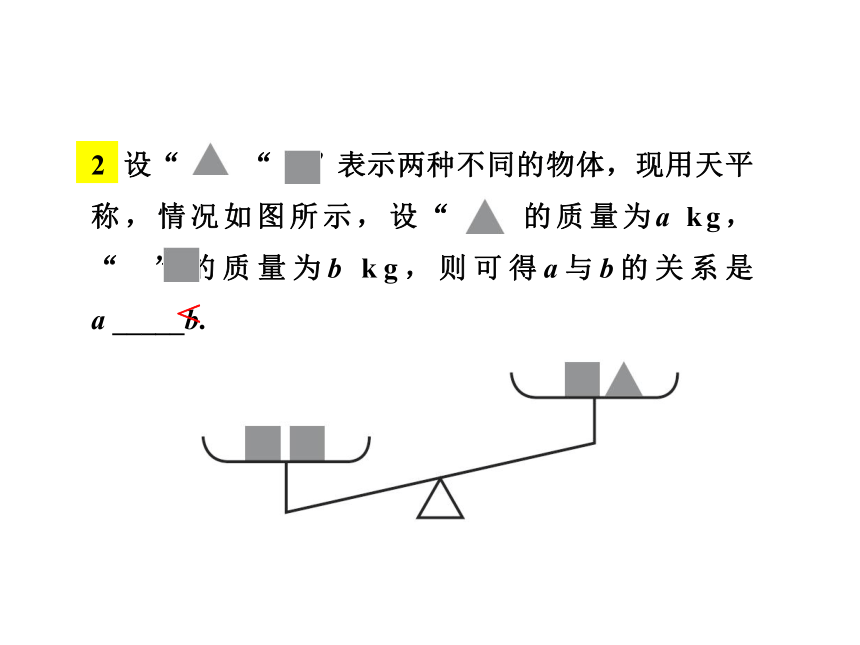
设“
”“
”表示两种不同的物体,现用天平
称,情况如图所示,设“
”的质量为a
kg,
“
”的质量为b
kg,则可得a与b的关系是
a
_____b.
<
2
知识点
不等式的性质2
比较大小
由此我们可以得到:不等式的两边都乘以(或除以)
同一个正数,不等号的方向不变.
(-16)__(-
24);
(-16)×4__(-
24)×4;
(-16)÷3__(-24)÷3
8__12;
8×4__12×4;
8÷3__12÷3
合作探究
不等式的性质2
不等式两边乘(或除以)同一个
正数,不等号的方向不变.即
如果
a>b,c>0,那么ac>bc
新知小结
已知实数a、b
,若a>b
,则下列结论正确的是
(
)
A.a-5<b-5
B.2+a<2+b
C.
D.3a>3b
不等式的两边同时加上或减去一个数,不等号的方
向不变,不等式的两边同时除以或乘以一个正数,
不等号的方向也不变,所以A、B、C错误,选D.
解析:
例2
D
合作探究
在应用不等式的基本性质2时,除了注意“两同”
要求外,还要注意“正数”的要求;另外,乘除运
算可以灵活选择.
新知小结
用不等式的性质解下列不等式,并在数轴上表示解集:
(1)x+5>-1;
(2)4x<3x-5.
(4)-8x>10.
1
巩固新知
(1)根据不等式的性质1,不等式两边都减去5,
得x+5-5>-1-5,
所以x>-6.
在数轴上表示这个不等式的解集如图所示.
解:
(2)根据不等式的性质1,不等式两边都减去3x,
得4x-3x<3x-5-3x,
所以x<-5.
在数轴上表示这个不等式的解集如图所示.
(3)根据不等式的性质2,不等式两边都乘以7
(或除以
),
得
,
所以x<6.
在数轴上表示这个不等式的解集如图所示.
(4)根据不等式的性质3,不等式两边都除以-8
(或乘以
),
得(-8x)÷(-8)<10÷(-8)
(或(-8x)×
<10×
),
所以x<
在数轴上表示这个不等式的解集如图所示.
2
若a是实数,x>y,则下列不等式中,正确的
是( )
A.ax>ay
B.a2x≤a2y
C.a2x>a2y
D.a2x≥a2y
D
3 (中考·南充)若m>n,则下列不等式不一定成立的是( )
A.m+2>n+2
B.2m>2n
C.
D.m2<n2
D
3
知识点
不等式的性质3
做一做
完成下列填空:
2×(-1)_______3×(-1);
2×(-5)_______3×(-5);
你发现了什么?请再举几例试一试,还有类似的结
论吗?与同伴交流.
>
>
>
合作探究
不等式的性质3
不等式两边乘(或除以)同一个负数
不等号的方向改变.
如果a>b,c<0,那么ac<bc
利用不等式的性质解下列不等式:
(1)
x-7>26;
(2)
3x<2x+1;
(3)
x>50;
(4)
-4x>3.
例3
解不等式,就是要借助不等式的性质使不等式
逐步化为x>a或
x<a
(a为常数)的形式.
分析:
(1)根据不等式的性质1,不等式两边加7,
不等号
的方向不变,所以
x-7+7>26+7,
x>33.
(2)根据不等式的性质1,不等式两边减2x,不等
号的方向不变,所以
3x-2x<2x+1-2x,
x<1.
解:
(3)根据不等式的性质2,
不等式两边乘
.
不等号
的方向不变,所以
x>75.
(4)根据不等式的性质3,
不等式两边除以-4,
不等
号的方向改变,所以
利用不等式的性质1可简化为“移项”;利用不
等式的性质2或性质3就是把未知数的系数化为1,要
注意不等式两边乘(或除以)同一个负数时,不等号要
改变方向.
新知小结
设a>b,用“<”或“>”填空:
a+2_____b+2;
(2)
a-3_____b-3;
(3)
-4a_____-4b;
(4)
1
>
>
<
>
巩固新知
2
【中考·株洲】已知实数a,b满足a+1>b+1,则下列选项错误的为( )
A.a>b
B.a+2>b+2
C.-a<-b
D.2a>3b
D
3
实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
A.a-c>b-c
B.a+cC.ac>bc
D.
B
不等式的基本性质:
不等式的基本性质1
不等式的两边都加(或减)
同一个整式,不等号的方向不变.
不等式的基本性质2
不等式两边都乘(或除以)同一
个正数,不等号的方向不变.
不等式的基本性质3
不等式两边都乘(或除以)同一
个负数,不等号的方向改变.
1
知识小结
归纳新知
1.不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
即如果a>b,那么a±c______b±c.
>
课后练习
2.下列推理正确的是( )
A.因为a<b,所以a+2<b+1
B.因为a<b,所以a-1<b-2
C.因为a>b,所以a+c>b+c
D.因为a>b,所以a+c>b-d
C
3.(2020·杭州)若a>b,则( )
A.a-1≥b
B.b+1≥a
C.a+1>b-1
D.a-1>b+1
【点拨】举出反例即可判断A,B,D,根据不等式的传递性即可判断C.
A.设a=0.5,b=0.4,a>b,但是a-1<b,不符合题意;
B.设a=3,b=1,a>b,但是b+1<a,不符合题意;
C.∵a>b,∴a+1>b+1,∵b+1>b-1,∴a+1>b-1,符合题意;
D.设a=0.5,b=0.4,a>b,但是a-1<b+1,不符合题意.
【答案】C
>
>
5.(中考·常州)若3x>-3y,则下列不等式中一定成立的是( )
A.x+y>0
B.x-y>0
C.x+y<0
D.x-y<0
A
【点拨】两边除以3,得x>-y;两边加y,得x+y>0.
【点拨】当c=0时,ac2>bc2不成立.
C
6.(中考·乐山)下列说法不一定成立的是( )
A.若a>b,则a+c>b+c
B.若a+c>b+c,则a>b
C.若a>b,则ac2>bc2
D.若ac2>bc2,则a>b
A
负
<
<
D
D
11.若实数a,b,c在数轴上对应点的位置如图所示,则下列不等式成立的是( )
A.ac>bc
B.ab>cb
C.a+c>b+c
D.a+b>c+b
【点拨】由题图知a<b<0<c,不等式a<b的两边同乘c,得ac<bc,∴A不符合题意;
不等式a<c的两边同乘b,得ab>cb,∴B符合题意;
不等式a<b的两边同加c,得a+c<b+c,∴C不符合题意;
不等式a<c的两边同加b,得a+b<c+b,∴D不符合题意.
【答案】B
D
C
14.若x<y,试比较下列各式的大小并说明理由.
(1)3x-1与3y-1;
解:3x-1<3y-1.理由如下:
∵x<y,∴3x<3y(不等式的性质2).
∴3x-1<3y-1(不等式的性质1).
(2)由a<b,得ma>mb;
解:m>0;
(3)由a>-5,得a2≤-5a;
m<0;
(4)由3x>4y,得3x-m>4y-m.
-5<a≤0;
m为任意实数.
解:由已知得1-a<0,即a>1,
则|a-1|+|a+2|=a-1+a+2=2a+1.
17.(1)①如果a-b<0,那么a________b;
②如果a-b=0,那么a________b;
③如果a-b>0,那么a________b.
(2)由(1)你能归纳出比较a和b大小的方法吗?请写出来.
<
=
>
解:可以通过作差来比较a和b的大小,当a-b<0时,a当a-b=0时,a=b;
当a-b>0时,a>b.
(3)用(2)的方法你能否比较2x2-x+7与x2-x-2的大小?
解:(2x2-x+7)-(x2-x-2)=2x2-x+7-x2+x+2
=x2+9>0,
∴2x2-x+7>x2-x-2.
18.阅读下列材料:
【提出问题】已知x-y=2,且x>1,y<0,试确定x+y的取值范围.
【解决问题】∵x-y=2,∴x=y+2.
又∵x>1,∴y+2>1,∴y>-1.
又∵y<0,∴-1<y<0.①
同理得1<x<2.②
由②+①得-1+1<y+x<0+2,
∴x+y的取值范围是0<x+y<2.
【尝试应用】完成任务:
(1)在提出问题中的条件下,求2x+3y的取值范围;
【思路点拨】运用类比思想,参照数学问题中的解法,结合不等式的性质求解.
解:∵1<x<2,∴2<2x<4.
∵-1<y<0,∴-3<3y<0.
∴-1<2x+3y<4.
(2)已知x+y=3,且x>2,y>0,求x-y的取值范围;
解:∵x+y=3,∴x=3-y.
又∵x>2,∴3-y>2.∴y<1.
又∵y>0,∴0<y<1.
∴-1<-y<0.
同理得2<x<3,∴-1+2<x-y<0+3.
∴x-y的取值范围是1<x-y<3.
解:∵x-y=a,∴x=a+y.
又∵x<-1,∴a+y<-1.
∴y<-1-a.
又∵y>1,∴-1-a>1.
∴a<-2.
当a<-2时,1<y<-1-a.
同理得1+a<x<-1,∴2+a<x+y<-a-2.
∴当a<-2时,x+y的取值范围是2+a<x+y<-a-2.
(3)已知y>1,x<-1,若x-y=a成立,求x+y的取值范围(结果用含a的式子表示).
再见
第九章
9.1.2
不等式的性质
人教版数学七年级下册
1.经历通过类比、猜测、验证发现不等式基本性质的探索过程,初步体会不等式与等式的异同。
2.掌握不等式的基本性质,并能初步运用不等式的基本性质将比较简单的不等式转化为“x>a”或“x<a”的形式。
学习目标
1
知识点
不等式的性质1
我们知道,等式两边加或减同一个数(或式子),
乘或除以同一个数(除数不为0),结果仍相等.
不等
式是否也有类似的性质呢?
合作探究
如果在不等式的两边都加或都减同一个整式,
那么结果会怎样?请举几例试一试,并与同伴交流.
思考
用“>”或“<”填空,并总结其中的规律:
(1)
5>3,
5+2
3+2,
5-2
3-2;
(2)
1<3,-1
+
2
3
+
2,
-1-3
3
–
3.
不等式的性质1
不等式两边加(或减)同一个数(或
式子)
,不等号的方向不变.
如果a>b,那么a±c>b±c.
新知小结
从变形来看,是利用了不等式的性质1.
(1)根据不等式性质1,不等式两边同时减去6;
(2)根据不等式性质1,不等式两边同时减去6x.
分析:
例1
指出下列不等式是如何变形的,并说明其变形的依据.
(1)若6+y>-7,则y>-13;
(2)若7x<6x+3,则x<3.
解:
合作探究
判断某个不等式变形的根据,
一看不等号的方向是不是改变,
二看式子的变化情况.
新知小结
1
已知a<b,用“>”或“<”填空:
(1)a+2________b+2;
(2)a-3________b-3;
(3)a+c________b+c;
(4)a-b________0.
<
<
<
<
巩固新知
2
设“
”“
”表示两种不同的物体,现用天平
称,情况如图所示,设“
”的质量为a
kg,
“
”的质量为b
kg,则可得a与b的关系是
a
_____b.
<
2
知识点
不等式的性质2
比较大小
由此我们可以得到:不等式的两边都乘以(或除以)
同一个正数,不等号的方向不变.
(-16)__(-
24);
(-16)×4__(-
24)×4;
(-16)÷3__(-24)÷3
8__12;
8×4__12×4;
8÷3__12÷3
合作探究
不等式的性质2
不等式两边乘(或除以)同一个
正数,不等号的方向不变.即
如果
a>b,c>0,那么ac>bc
新知小结
已知实数a、b
,若a>b
,则下列结论正确的是
(
)
A.a-5<b-5
B.2+a<2+b
C.
D.3a>3b
不等式的两边同时加上或减去一个数,不等号的方
向不变,不等式的两边同时除以或乘以一个正数,
不等号的方向也不变,所以A、B、C错误,选D.
解析:
例2
D
合作探究
在应用不等式的基本性质2时,除了注意“两同”
要求外,还要注意“正数”的要求;另外,乘除运
算可以灵活选择.
新知小结
用不等式的性质解下列不等式,并在数轴上表示解集:
(1)x+5>-1;
(2)4x<3x-5.
(4)-8x>10.
1
巩固新知
(1)根据不等式的性质1,不等式两边都减去5,
得x+5-5>-1-5,
所以x>-6.
在数轴上表示这个不等式的解集如图所示.
解:
(2)根据不等式的性质1,不等式两边都减去3x,
得4x-3x<3x-5-3x,
所以x<-5.
在数轴上表示这个不等式的解集如图所示.
(3)根据不等式的性质2,不等式两边都乘以7
(或除以
),
得
,
所以x<6.
在数轴上表示这个不等式的解集如图所示.
(4)根据不等式的性质3,不等式两边都除以-8
(或乘以
),
得(-8x)÷(-8)<10÷(-8)
(或(-8x)×
<10×
),
所以x<
在数轴上表示这个不等式的解集如图所示.
2
若a是实数,x>y,则下列不等式中,正确的
是( )
A.ax>ay
B.a2x≤a2y
C.a2x>a2y
D.a2x≥a2y
D
3 (中考·南充)若m>n,则下列不等式不一定成立的是( )
A.m+2>n+2
B.2m>2n
C.
D.m2<n2
D
3
知识点
不等式的性质3
做一做
完成下列填空:
2×(-1)_______3×(-1);
2×(-5)_______3×(-5);
你发现了什么?请再举几例试一试,还有类似的结
论吗?与同伴交流.
>
>
>
合作探究
不等式的性质3
不等式两边乘(或除以)同一个负数
不等号的方向改变.
如果a>b,c<0,那么ac<bc
利用不等式的性质解下列不等式:
(1)
x-7>26;
(2)
3x<2x+1;
(3)
x>50;
(4)
-4x>3.
例3
解不等式,就是要借助不等式的性质使不等式
逐步化为x>a或
x<a
(a为常数)的形式.
分析:
(1)根据不等式的性质1,不等式两边加7,
不等号
的方向不变,所以
x-7+7>26+7,
x>33.
(2)根据不等式的性质1,不等式两边减2x,不等
号的方向不变,所以
3x-2x<2x+1-2x,
x<1.
解:
(3)根据不等式的性质2,
不等式两边乘
.
不等号
的方向不变,所以
x>75.
(4)根据不等式的性质3,
不等式两边除以-4,
不等
号的方向改变,所以
利用不等式的性质1可简化为“移项”;利用不
等式的性质2或性质3就是把未知数的系数化为1,要
注意不等式两边乘(或除以)同一个负数时,不等号要
改变方向.
新知小结
设a>b,用“<”或“>”填空:
a+2_____b+2;
(2)
a-3_____b-3;
(3)
-4a_____-4b;
(4)
1
>
>
<
>
巩固新知
2
【中考·株洲】已知实数a,b满足a+1>b+1,则下列选项错误的为( )
A.a>b
B.a+2>b+2
C.-a<-b
D.2a>3b
D
3
实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
A.a-c>b-c
B.a+c
D.
B
不等式的基本性质:
不等式的基本性质1
不等式的两边都加(或减)
同一个整式,不等号的方向不变.
不等式的基本性质2
不等式两边都乘(或除以)同一
个正数,不等号的方向不变.
不等式的基本性质3
不等式两边都乘(或除以)同一
个负数,不等号的方向改变.
1
知识小结
归纳新知
1.不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
即如果a>b,那么a±c______b±c.
>
课后练习
2.下列推理正确的是( )
A.因为a<b,所以a+2<b+1
B.因为a<b,所以a-1<b-2
C.因为a>b,所以a+c>b+c
D.因为a>b,所以a+c>b-d
C
3.(2020·杭州)若a>b,则( )
A.a-1≥b
B.b+1≥a
C.a+1>b-1
D.a-1>b+1
【点拨】举出反例即可判断A,B,D,根据不等式的传递性即可判断C.
A.设a=0.5,b=0.4,a>b,但是a-1<b,不符合题意;
B.设a=3,b=1,a>b,但是b+1<a,不符合题意;
C.∵a>b,∴a+1>b+1,∵b+1>b-1,∴a+1>b-1,符合题意;
D.设a=0.5,b=0.4,a>b,但是a-1<b+1,不符合题意.
【答案】C
>
>
5.(中考·常州)若3x>-3y,则下列不等式中一定成立的是( )
A.x+y>0
B.x-y>0
C.x+y<0
D.x-y<0
A
【点拨】两边除以3,得x>-y;两边加y,得x+y>0.
【点拨】当c=0时,ac2>bc2不成立.
C
6.(中考·乐山)下列说法不一定成立的是( )
A.若a>b,则a+c>b+c
B.若a+c>b+c,则a>b
C.若a>b,则ac2>bc2
D.若ac2>bc2,则a>b
A
负
<
<
D
D
11.若实数a,b,c在数轴上对应点的位置如图所示,则下列不等式成立的是( )
A.ac>bc
B.ab>cb
C.a+c>b+c
D.a+b>c+b
【点拨】由题图知a<b<0<c,不等式a<b的两边同乘c,得ac<bc,∴A不符合题意;
不等式a<c的两边同乘b,得ab>cb,∴B符合题意;
不等式a<b的两边同加c,得a+c<b+c,∴C不符合题意;
不等式a<c的两边同加b,得a+b<c+b,∴D不符合题意.
【答案】B
D
C
14.若x<y,试比较下列各式的大小并说明理由.
(1)3x-1与3y-1;
解:3x-1<3y-1.理由如下:
∵x<y,∴3x<3y(不等式的性质2).
∴3x-1<3y-1(不等式的性质1).
(2)由a<b,得ma>mb;
解:m>0;
(3)由a>-5,得a2≤-5a;
m<0;
(4)由3x>4y,得3x-m>4y-m.
-5<a≤0;
m为任意实数.
解:由已知得1-a<0,即a>1,
则|a-1|+|a+2|=a-1+a+2=2a+1.
17.(1)①如果a-b<0,那么a________b;
②如果a-b=0,那么a________b;
③如果a-b>0,那么a________b.
(2)由(1)你能归纳出比较a和b大小的方法吗?请写出来.
<
=
>
解:可以通过作差来比较a和b的大小,当a-b<0时,a
当a-b>0时,a>b.
(3)用(2)的方法你能否比较2x2-x+7与x2-x-2的大小?
解:(2x2-x+7)-(x2-x-2)=2x2-x+7-x2+x+2
=x2+9>0,
∴2x2-x+7>x2-x-2.
18.阅读下列材料:
【提出问题】已知x-y=2,且x>1,y<0,试确定x+y的取值范围.
【解决问题】∵x-y=2,∴x=y+2.
又∵x>1,∴y+2>1,∴y>-1.
又∵y<0,∴-1<y<0.①
同理得1<x<2.②
由②+①得-1+1<y+x<0+2,
∴x+y的取值范围是0<x+y<2.
【尝试应用】完成任务:
(1)在提出问题中的条件下,求2x+3y的取值范围;
【思路点拨】运用类比思想,参照数学问题中的解法,结合不等式的性质求解.
解:∵1<x<2,∴2<2x<4.
∵-1<y<0,∴-3<3y<0.
∴-1<2x+3y<4.
(2)已知x+y=3,且x>2,y>0,求x-y的取值范围;
解:∵x+y=3,∴x=3-y.
又∵x>2,∴3-y>2.∴y<1.
又∵y>0,∴0<y<1.
∴-1<-y<0.
同理得2<x<3,∴-1+2<x-y<0+3.
∴x-y的取值范围是1<x-y<3.
解:∵x-y=a,∴x=a+y.
又∵x<-1,∴a+y<-1.
∴y<-1-a.
又∵y>1,∴-1-a>1.
∴a<-2.
当a<-2时,1<y<-1-a.
同理得1+a<x<-1,∴2+a<x+y<-a-2.
∴当a<-2时,x+y的取值范围是2+a<x+y<-a-2.
(3)已知y>1,x<-1,若x-y=a成立,求x+y的取值范围(结果用含a的式子表示).
再见
