江西省南昌二中2011-2012学年高二上学期期末考试数学(理)试题
文档属性
| 名称 | 江西省南昌二中2011-2012学年高二上学期期末考试数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 634.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-30 09:23:29 | ||
图片预览

文档简介
江西省南昌二中2011-2012学年高二上学期期末考试
数学(理)试题
一、选择题(每小题5分,满分50分)
1.命题“若x2+y2=0,则x,y全为0”的否命题是( )
A.若x2+y2≠0,则x,y全不为0. B.若x2+y2≠0,则x,y不全为0.
C.若x2+y2≠0,则x,y至少有一个为0. D.若x,y不全为0,则x2+y2≠0.
2.已知M是平面上一动点,F1,F3是平面上两定点,P:|MF1|+|MF2|为正常数,
q:M点轨迹是以F1,F3为焦点的椭圆,则p是q的( )
A.充要条件 B.充分而不必要条件
C.必要而不充分条件 D.既不充分也不必要条件
3.在空间直角坐标系0-xyz中,点A(-1,2,3)点B(3,-2,-1),点p在线段AB上,
且OP⊥AB,则P点坐标是( )
A.(1,0,1) B.(-1,-1,0) C.(0,-1,1) D.(1,1,0)
4.命题“”的否定是( )
A. B.
C. D.
5.直线a,b的方向向量分别为,则a与b的位置关系是( )
A.平行 B.重合 C.垂直 D.夹角等于
6.已知椭圆的短轴长为4,离心率e=,中心在原点,焦点在坐标轴上,其标准方程是( )
A. B.
C. D.
7.如图,正方体ABCD-A1B1C1D1的棱长为2,P点在A1C1上,且AP∥平面BDC1,则p点的坐标是( )
A.(, ,2) B.(1,1,2)
C.( ,,2) D.( ,,)
8.经过y2=4x焦点的直线与抛物线交于A,B两点,已知A点到抛物线的准线的距离为5,则B点坐标是( )
A.(1,2)或(1,-2) B.(4,-4)或(4,4)
C.( ,)或(,-) D.( ,1)或(,-1)
9.如图,将三棱锥A-BCD的侧面沿侧棱AB,AC,AD剪开,并和底面展平,恰好构成一个正 角形,则在三棱锥A-BCD中,AB与CD所成的角大小为( )
A.30° B.45° C.60° D.90°
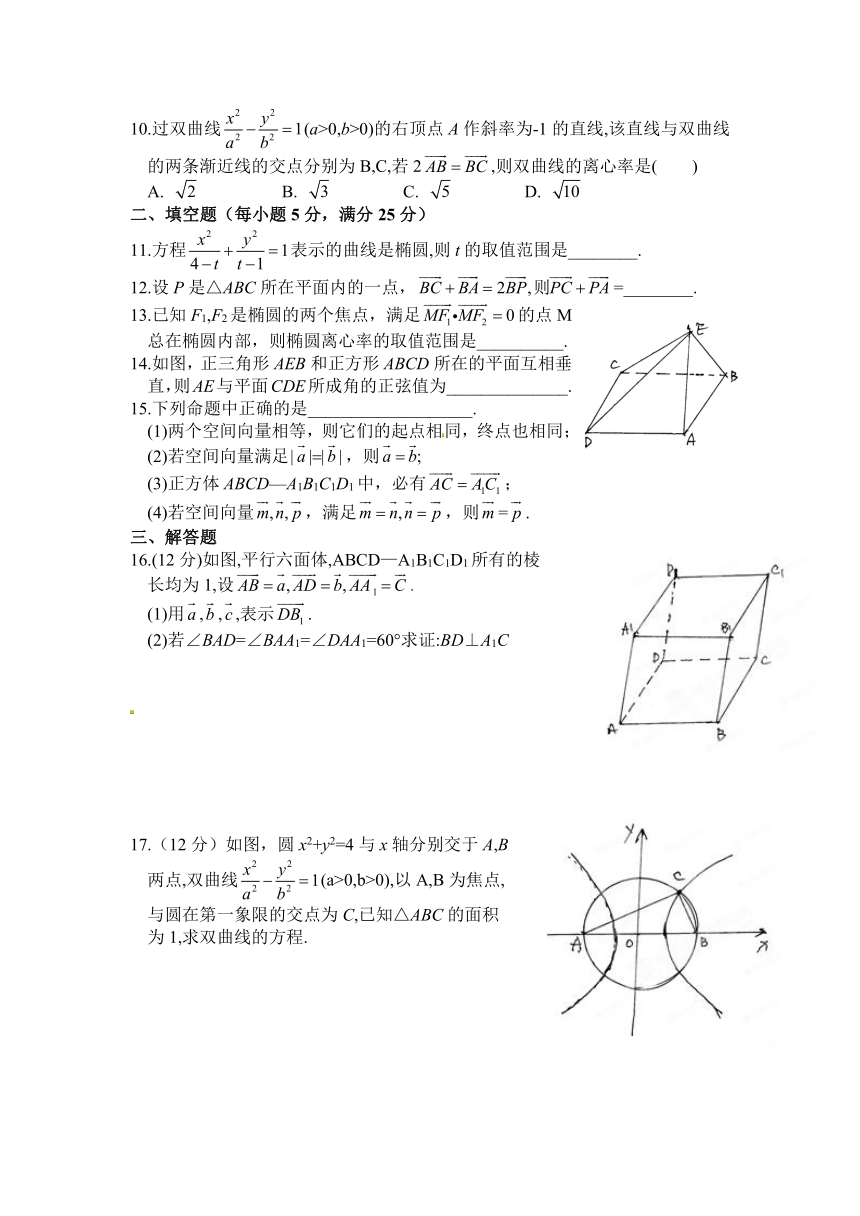
10.过双曲线(a>0,b>0)的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B,C,若2,则双曲线的离心率是( )
A. B. C. D.
二、填空题(每小题5分,满分25分)
11.方程表示的曲线是椭圆,则t的取值范围是________.
12.设P是△ABC所在平面内的一点,=________.
13.已知F1,F2是椭圆的两个焦点,满足的点M
总在椭圆内部,则椭圆离心率的取值范围是__________.
14.如图,正三角形AEB和正方形ABCD所在的平面互相垂
直,则AE与平面CDE所成角的正弦值为______________.
15.下列命题中正确的是___________________.
(1)两个空间向量相等,则它们的起点相同,终点也相同;
(2)若空间向量满足,则
(3)正方体ABCD—A1B1C1D1中,必有;
(4)若空间向量,满足,则=.
三、解答题
16.(12分)如图,平行六面体,ABCD—A1B1C1D1所有的棱
长均为1,设.
(1)用,,,表示.
(2)若∠BAD=∠BAA1=∠DAA1=60°求证:BD⊥A1C
17.(12分)如图,圆x2+y2=4与x轴分别交于A,B
两点,双曲线(a>0,b>0),以A,B为焦点,
与圆在第一象限的交点为C,已知△ABC的面积
为1,求双曲线的方程.
18.(12分)如图,正方体ABCD—A1B1C1D1的棱长为2,E,F,G,H分别为
A1B1,A1D1,BB1,A1C1的中点.
(1)求证:CH∥平面EFG.
(2)求C点到平面EFG的距离.
19.(12分)已知P:关于x的不等式(a-1)x>1的解集是{x|x<0},q:a2-2ta+t2-1<0,
若p是q的必要非充分条件,求实数t的取值范围.
20.(13分)如图,等腰直角三角形AEC(∠AEC=90°)所在的平面与菱形ABCD所
在的平面相交于直线AC,二面角E—AC—B=135°,BD=AC.
(1)求证:AC⊥DE.
(2)设G是△ECD的重心,求二面角B—EG—C的余弦值.
21.(14分)若A,B是抛物线y2=4x上的不同两点,弦AB(不平行y轴)的垂直
平分线与x轴相交于点p,则称AB是点P的一条“相关弦”,已知当x>2时,点P(x,0)存在无穷多条“相关弦”,给定x0>2。
(1)求点P(6,0)的所有“相关弦”的中点的横坐标;
(2)试问:点P(x0,0)的“相关弦”的弦长中是否存在最大值?若存在,求其最大值(用x0表示);若不存在,请说明理由.
数学(理)试题
一、选择题(每小题5分,满分50分)
1.命题“若x2+y2=0,则x,y全为0”的否命题是( )
A.若x2+y2≠0,则x,y全不为0. B.若x2+y2≠0,则x,y不全为0.
C.若x2+y2≠0,则x,y至少有一个为0. D.若x,y不全为0,则x2+y2≠0.
2.已知M是平面上一动点,F1,F3是平面上两定点,P:|MF1|+|MF2|为正常数,
q:M点轨迹是以F1,F3为焦点的椭圆,则p是q的( )
A.充要条件 B.充分而不必要条件
C.必要而不充分条件 D.既不充分也不必要条件
3.在空间直角坐标系0-xyz中,点A(-1,2,3)点B(3,-2,-1),点p在线段AB上,
且OP⊥AB,则P点坐标是( )
A.(1,0,1) B.(-1,-1,0) C.(0,-1,1) D.(1,1,0)
4.命题“”的否定是( )
A. B.
C. D.
5.直线a,b的方向向量分别为,则a与b的位置关系是( )
A.平行 B.重合 C.垂直 D.夹角等于
6.已知椭圆的短轴长为4,离心率e=,中心在原点,焦点在坐标轴上,其标准方程是( )
A. B.
C. D.
7.如图,正方体ABCD-A1B1C1D1的棱长为2,P点在A1C1上,且AP∥平面BDC1,则p点的坐标是( )
A.(, ,2) B.(1,1,2)
C.( ,,2) D.( ,,)
8.经过y2=4x焦点的直线与抛物线交于A,B两点,已知A点到抛物线的准线的距离为5,则B点坐标是( )
A.(1,2)或(1,-2) B.(4,-4)或(4,4)
C.( ,)或(,-) D.( ,1)或(,-1)
9.如图,将三棱锥A-BCD的侧面沿侧棱AB,AC,AD剪开,并和底面展平,恰好构成一个正 角形,则在三棱锥A-BCD中,AB与CD所成的角大小为( )
A.30° B.45° C.60° D.90°
10.过双曲线(a>0,b>0)的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B,C,若2,则双曲线的离心率是( )
A. B. C. D.
二、填空题(每小题5分,满分25分)
11.方程表示的曲线是椭圆,则t的取值范围是________.
12.设P是△ABC所在平面内的一点,=________.
13.已知F1,F2是椭圆的两个焦点,满足的点M
总在椭圆内部,则椭圆离心率的取值范围是__________.
14.如图,正三角形AEB和正方形ABCD所在的平面互相垂
直,则AE与平面CDE所成角的正弦值为______________.
15.下列命题中正确的是___________________.
(1)两个空间向量相等,则它们的起点相同,终点也相同;
(2)若空间向量满足,则
(3)正方体ABCD—A1B1C1D1中,必有;
(4)若空间向量,满足,则=.
三、解答题
16.(12分)如图,平行六面体,ABCD—A1B1C1D1所有的棱
长均为1,设.
(1)用,,,表示.
(2)若∠BAD=∠BAA1=∠DAA1=60°求证:BD⊥A1C
17.(12分)如图,圆x2+y2=4与x轴分别交于A,B
两点,双曲线(a>0,b>0),以A,B为焦点,
与圆在第一象限的交点为C,已知△ABC的面积
为1,求双曲线的方程.
18.(12分)如图,正方体ABCD—A1B1C1D1的棱长为2,E,F,G,H分别为
A1B1,A1D1,BB1,A1C1的中点.
(1)求证:CH∥平面EFG.
(2)求C点到平面EFG的距离.
19.(12分)已知P:关于x的不等式(a-1)x>1的解集是{x|x<0},q:a2-2ta+t2-1<0,
若p是q的必要非充分条件,求实数t的取值范围.
20.(13分)如图,等腰直角三角形AEC(∠AEC=90°)所在的平面与菱形ABCD所
在的平面相交于直线AC,二面角E—AC—B=135°,BD=AC.
(1)求证:AC⊥DE.
(2)设G是△ECD的重心,求二面角B—EG—C的余弦值.
21.(14分)若A,B是抛物线y2=4x上的不同两点,弦AB(不平行y轴)的垂直
平分线与x轴相交于点p,则称AB是点P的一条“相关弦”,已知当x>2时,点P(x,0)存在无穷多条“相关弦”,给定x0>2。
(1)求点P(6,0)的所有“相关弦”的中点的横坐标;
(2)试问:点P(x0,0)的“相关弦”的弦长中是否存在最大值?若存在,求其最大值(用x0表示);若不存在,请说明理由.
同课章节目录
