6.1平面向量的概念-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(25张)
文档属性
| 名称 | 6.1平面向量的概念-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(25张) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
第六章
平面向量及其应用
45°
东
南
西
北
A
B
高尔夫球是一项非常有趣的运动,这项运动需要全身器官的整体协调,而击球的关键在于两个“D”,即方向(Direction)和距离(Distance),初学者中有不少人只想把球打远,而忽视方向的重要性,其实,把球打直要比打远更重要!
所以擅长打高尔夫的人都会谨记这样一个原则:“方向比距离更重要”.
方向走对了,哪怕走得慢却能一步一步靠近成功;可倘若走错了方向,不仅白忙活一场,更可能离成功越来越远.
在现实生活中,我们会遇到很多量,其中一些量在取定单位后只用一个实数就可以表示出来,如长度、质量等.
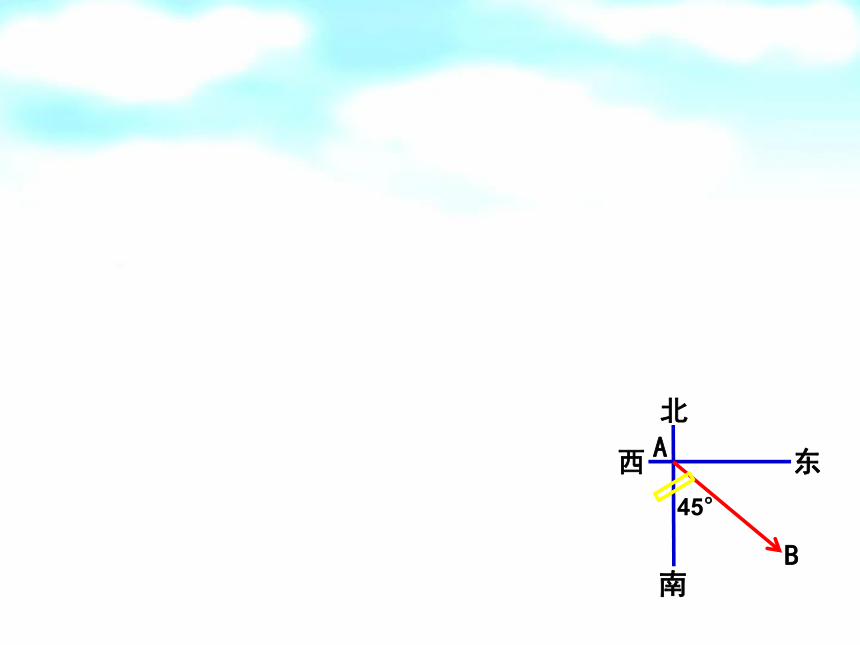
还有一些量则不是这样,例如上图中的小船的位移,小船由A地向东南方向航行15
n
mile到达B地(速度的大小为10
n
mile/h).
这里,如果仅指出“由A地航行15
n
mile”,而不指明“向东南方向”航行,那么小船就不一定到达B地了.
这就是说,位移是既有大小又有方向的量.
力、速度、加速度等也是这样的量.对这种既有大小又有方向的量加以抽象,就得到了我们本章将要研究的向量.
向量是近代数学中重要和基本的概念之一,向量理论具有丰富的物理背景、深刻的数学内涵.向量既是代数研究对象,也是几何研究对象,是沟通几何与代数的桥梁,是进一步学习和研究其他数学领域问题的基础,在解决实际问题中发挥着重要作用.
本章我们将通过实际背景引入向量的概念,类比数的运算学习向量的运算及其性质,建立向量的运算体系.在此基础上,用向量的语言、方法表述和解决现实生活、数学和物理中的一些问题.
6.1平面向量的概念
一、向量的实际背景
G
F
在本章引言中,小船位移的大小是A、B两地之间的距离15
n
mile,位移的方向是东南方向;小船航行速度的大小是10
n
mile/h,
速度的方向是东南方向.
位移和速度有各自的特性,但也有共同属性,请问共同属性是什么?
既有大小,又有方向.
在物理学中还有没有具有这种属性的量?
有,比如“力”
我们知道,从一支笔、一棵树、一本书??????中,可以抽象出只有大小的数量“1”.类似地,我们可以对力、位移、速度??????这些量进行抽象,形成一种新的量.
二、向量的概念
既有大小,又有方向的量叫做向量.
只有大小,没有方向的量叫做数量.
如力、位移、速度.
如年龄、身高、长度、面积、体积、质量.
物理学中,常称:
向量为矢量,数量为标量.
你还能举出物理学中的一些向量和数量吗?
加速度是向量,时间、路程、功是数量.
一、探究
问题:在质量、重力、速度、加速度、身高、面积、体积这些量中,哪些是既有大小又有方向?哪些是只有大小没有方向?
只有大小没有方向有:
既有大小又有方向有:
质量、身高、面积、体积
重力、速度、加速度
既有大小又有方向的量
二、基础知识讲解
1、向量的概念
问题:数量与向量有何区别?
数量:只有大小,没有方向的量
2、向量的表示方法
向量常用有向线段表示:线段按一定的比例画出,其长度表示向量的大小,箭头所指的方向表示向量的方向。
(1)几何表示:
有向线段:带有方向的线段
向量的模
向量的长度
A
B
(2)字母表示:
大小记作:
2、向量的表示方法
(1)几何表示:有向线段
二、基础知识讲解
注:如图,以A为起点,B为终点的有向线段表示的向量记为
,其中线段的长度记作
(读为向量
的模)
思考:
“向量就是有向线段,有向线段就是向量.”的说法对吗?
A
B
(2)字母表示:
2、向量的表示方法
(1)几何表示:有向线段
二、基础知识讲解
1、向量:与起点无关。用有向线段表示向量时,起点可以取任意位置。数学中的向量也叫自由向量。
注意:
2、有向线段与向量的区别:
有向线段:三要素:起点、大小、方向
向量:可选任意点作为向量的起点、有大小、有方向
A
B
C
D
A
B
C
D
有向线段
是不同的
1、向量:与起点无关。用有向线段表示向量时,起点可以取任意位置。数学中的向量也叫自由向量。
注意:
2、有向线段与向量的区别:
有向线段:三要素:起点、大小、方向
向量:可选任意点作为向量的起点、有大小、有方向
向量
是同一个向量
1.温度含零上和零下温度,所以温度是向量(
)
判断题
×
×
2.向量的模是一个正实数。(
)
×
注:向量不能比较大小
长度相等且方向相同的两个向量表示相等向量,
但是两个向量之间只有相等关系,没有大小之分,“对于向量
,
,
>
,或
<
”这种说法是错误的.
3.若|a|>|b|
,则a
>
b
(
)
3、两个特殊的向量:零向量、单位向量
零向量:长度为0的向量,记为
;
注②、零向量、单位向量都是只限制大小,不确定方向的
单位向量:长度为1的向量。
注①、规定:零向量的方向是任意的
4、平行向量
:方向相同或相反的非零向量叫平行向量
注①、若是平行向量,则记为
注②、规定:零向量与任一向量平行,即对任意向量
,都有
二、基础知识讲解
5、相等向量:
长度相等且方向相同的向量叫相等向量
注:1、若向量
相等,则记为
;
2、零向量与零向量相等
3、任意两个相等的非零向量,都可用同一条有向线段来表示,并且与有向线段的起点无关。
a
b
c
a=b=c
A1B1=A2B2=A3B3=A4B4
A1
B1
A2
B2
A3
B3
A4
B4
二、基础知识讲解
6、共线向量与平行向量
:平行向量也叫共线向量
注:任一组平行向量都可以平移到同一直线上.
(与有向线段的起点无关)
练习:判断下列各组向量是否平行?
A
B
C
①
④
A
B
C
③
②
说明:1、平行向量可以在同一直线上,要区别于两平行线的位置关系.
2、共线向量可以互相平行,要区别于在一直线上的线段的位置关系.
二、基础知识讲解
例1、试根据图中的比例尺以及三地的位置,在图中分别用向量表示A地至B、C两地的位移,并求出A地至B、C两地的实际距离(精确到1km).
1:8000000
三、例题讲解
例2、如图,设O是正六边形ABCDEF的中心,分别写出图中与
相等的向量。
O
A
B
C
D
E
F
三、例题分析
四、针对性练习
×
√
×
×
×
×
×
√
×
D
四、针对性练习
√
×
四、针对性练习
相同
相等
1、向量的概念;
2、向量的表示;
3、向量的模;
4、两个特殊的向量:零向量、单位向量;
5、相等向量;
6、平行向量与共线向量
五、课时小结
练习:
C
D
x=-2
x=2
第六章
平面向量及其应用
45°
东
南
西
北
A
B
高尔夫球是一项非常有趣的运动,这项运动需要全身器官的整体协调,而击球的关键在于两个“D”,即方向(Direction)和距离(Distance),初学者中有不少人只想把球打远,而忽视方向的重要性,其实,把球打直要比打远更重要!
所以擅长打高尔夫的人都会谨记这样一个原则:“方向比距离更重要”.
方向走对了,哪怕走得慢却能一步一步靠近成功;可倘若走错了方向,不仅白忙活一场,更可能离成功越来越远.
在现实生活中,我们会遇到很多量,其中一些量在取定单位后只用一个实数就可以表示出来,如长度、质量等.
还有一些量则不是这样,例如上图中的小船的位移,小船由A地向东南方向航行15
n
mile到达B地(速度的大小为10
n
mile/h).
这里,如果仅指出“由A地航行15
n
mile”,而不指明“向东南方向”航行,那么小船就不一定到达B地了.
这就是说,位移是既有大小又有方向的量.
力、速度、加速度等也是这样的量.对这种既有大小又有方向的量加以抽象,就得到了我们本章将要研究的向量.
向量是近代数学中重要和基本的概念之一,向量理论具有丰富的物理背景、深刻的数学内涵.向量既是代数研究对象,也是几何研究对象,是沟通几何与代数的桥梁,是进一步学习和研究其他数学领域问题的基础,在解决实际问题中发挥着重要作用.
本章我们将通过实际背景引入向量的概念,类比数的运算学习向量的运算及其性质,建立向量的运算体系.在此基础上,用向量的语言、方法表述和解决现实生活、数学和物理中的一些问题.
6.1平面向量的概念
一、向量的实际背景
G
F
在本章引言中,小船位移的大小是A、B两地之间的距离15
n
mile,位移的方向是东南方向;小船航行速度的大小是10
n
mile/h,
速度的方向是东南方向.
位移和速度有各自的特性,但也有共同属性,请问共同属性是什么?
既有大小,又有方向.
在物理学中还有没有具有这种属性的量?
有,比如“力”
我们知道,从一支笔、一棵树、一本书??????中,可以抽象出只有大小的数量“1”.类似地,我们可以对力、位移、速度??????这些量进行抽象,形成一种新的量.
二、向量的概念
既有大小,又有方向的量叫做向量.
只有大小,没有方向的量叫做数量.
如力、位移、速度.
如年龄、身高、长度、面积、体积、质量.
物理学中,常称:
向量为矢量,数量为标量.
你还能举出物理学中的一些向量和数量吗?
加速度是向量,时间、路程、功是数量.
一、探究
问题:在质量、重力、速度、加速度、身高、面积、体积这些量中,哪些是既有大小又有方向?哪些是只有大小没有方向?
只有大小没有方向有:
既有大小又有方向有:
质量、身高、面积、体积
重力、速度、加速度
既有大小又有方向的量
二、基础知识讲解
1、向量的概念
问题:数量与向量有何区别?
数量:只有大小,没有方向的量
2、向量的表示方法
向量常用有向线段表示:线段按一定的比例画出,其长度表示向量的大小,箭头所指的方向表示向量的方向。
(1)几何表示:
有向线段:带有方向的线段
向量的模
向量的长度
A
B
(2)字母表示:
大小记作:
2、向量的表示方法
(1)几何表示:有向线段
二、基础知识讲解
注:如图,以A为起点,B为终点的有向线段表示的向量记为
,其中线段的长度记作
(读为向量
的模)
思考:
“向量就是有向线段,有向线段就是向量.”的说法对吗?
A
B
(2)字母表示:
2、向量的表示方法
(1)几何表示:有向线段
二、基础知识讲解
1、向量:与起点无关。用有向线段表示向量时,起点可以取任意位置。数学中的向量也叫自由向量。
注意:
2、有向线段与向量的区别:
有向线段:三要素:起点、大小、方向
向量:可选任意点作为向量的起点、有大小、有方向
A
B
C
D
A
B
C
D
有向线段
是不同的
1、向量:与起点无关。用有向线段表示向量时,起点可以取任意位置。数学中的向量也叫自由向量。
注意:
2、有向线段与向量的区别:
有向线段:三要素:起点、大小、方向
向量:可选任意点作为向量的起点、有大小、有方向
向量
是同一个向量
1.温度含零上和零下温度,所以温度是向量(
)
判断题
×
×
2.向量的模是一个正实数。(
)
×
注:向量不能比较大小
长度相等且方向相同的两个向量表示相等向量,
但是两个向量之间只有相等关系,没有大小之分,“对于向量
,
,
>
,或
<
”这种说法是错误的.
3.若|a|>|b|
,则a
>
b
(
)
3、两个特殊的向量:零向量、单位向量
零向量:长度为0的向量,记为
;
注②、零向量、单位向量都是只限制大小,不确定方向的
单位向量:长度为1的向量。
注①、规定:零向量的方向是任意的
4、平行向量
:方向相同或相反的非零向量叫平行向量
注①、若是平行向量,则记为
注②、规定:零向量与任一向量平行,即对任意向量
,都有
二、基础知识讲解
5、相等向量:
长度相等且方向相同的向量叫相等向量
注:1、若向量
相等,则记为
;
2、零向量与零向量相等
3、任意两个相等的非零向量,都可用同一条有向线段来表示,并且与有向线段的起点无关。
a
b
c
a=b=c
A1B1=A2B2=A3B3=A4B4
A1
B1
A2
B2
A3
B3
A4
B4
二、基础知识讲解
6、共线向量与平行向量
:平行向量也叫共线向量
注:任一组平行向量都可以平移到同一直线上.
(与有向线段的起点无关)
练习:判断下列各组向量是否平行?
A
B
C
①
④
A
B
C
③
②
说明:1、平行向量可以在同一直线上,要区别于两平行线的位置关系.
2、共线向量可以互相平行,要区别于在一直线上的线段的位置关系.
二、基础知识讲解
例1、试根据图中的比例尺以及三地的位置,在图中分别用向量表示A地至B、C两地的位移,并求出A地至B、C两地的实际距离(精确到1km).
1:8000000
三、例题讲解
例2、如图,设O是正六边形ABCDEF的中心,分别写出图中与
相等的向量。
O
A
B
C
D
E
F
三、例题分析
四、针对性练习
×
√
×
×
×
×
×
√
×
D
四、针对性练习
√
×
四、针对性练习
相同
相等
1、向量的概念;
2、向量的表示;
3、向量的模;
4、两个特殊的向量:零向量、单位向量;
5、相等向量;
6、平行向量与共线向量
五、课时小结
练习:
C
D
x=-2
x=2
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
