北京市第43中学2020-2021学年第二学期九年级数学开学检测试题(word版,含答案)
文档属性
| 名称 | 北京市第43中学2020-2021学年第二学期九年级数学开学检测试题(word版,含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 589.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 00:00:00 | ||
图片预览

文档简介
北京市第四十三中学初三摸底检测2021.3
数 学
考生须知
1.本试卷共8页,共三道大题,25道小题,满分100分,考试时间120分钟.
2.在试卷上和答题卡上准确填写学校、班级、姓名和教育ID号.
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.
4.在答题卡上选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答.
5.考试结束后,请将答题卡交回.
一、选择题(本题共24分,每小题3分)
第1-8题均有四个选项,符合题意的选项只有一个.
1. 已知反比例函数y=kx的图像经过点A(1,3),则k的值为
A.3 B.4
C.5 D.6
2. 下列图形中,既是中心对称图形又是轴对称图形的是
A.直角三角形 B.等边三角形
C. 圆 D.四边形
3. 若关于x的方程ax2-2ax+1=0的一个根是-1,则a的值是
A. 1 B. -1
C. -13 D. -3
4. 不透明袋子中有2个红球和2个绿球,这些球除颜色外无其他差别.从袋子中随机取出1个球,恰好是红球的概率为
13 B.12
5448300234315C.23 D.1
5. 如图,ΔABC中,点D,E分别在边AB,AC的反向延长线上,且DE//BC.若AE=2,AC=4,AD=3,则AB为
9 B. 32
C.3 D.6
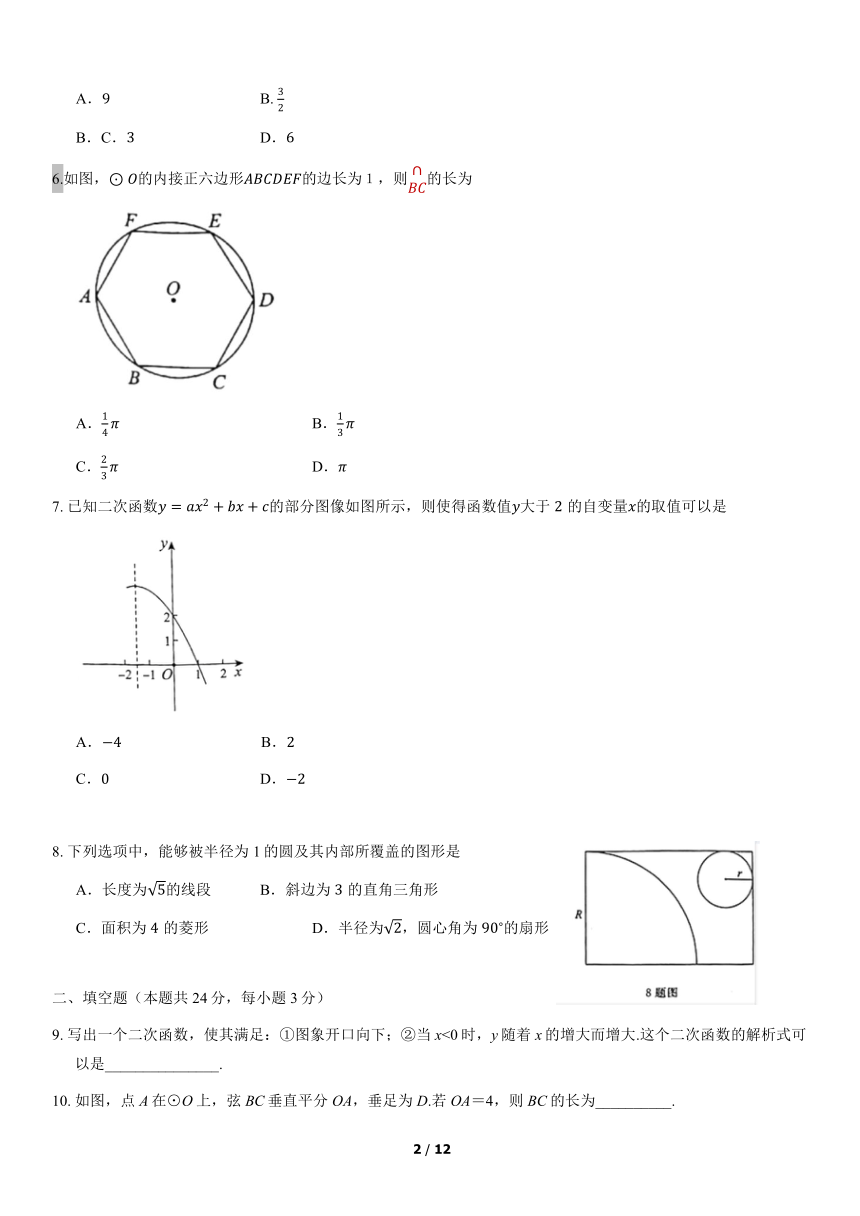
6.如图,⊙O的内接正六边形ABCDEF的边长为1,则∩BC的长为
14π B.13π
C.23π D.π
7. 已知二次函数y=ax2+bx+c的部分图像如图所示,则使得函数值y大于2的自变量x的取值可以是
A.-4 B.2
C.0 D.-2
443865063508. 下列选项中,能够被半径为1的圆及其内部所覆盖的图形是
A.长度为5的线段 B.斜边为3的直角三角形
C.面积为4的菱形 D.半径为2,圆心角为90?的扇形
二、填空题(本题共24分,每小题3分)
9. 写出一个二次函数,使其满足:①图象开口向下;②当x<0时,y随着x的增大而增大.这个二次函数的解析式可以是_______________.
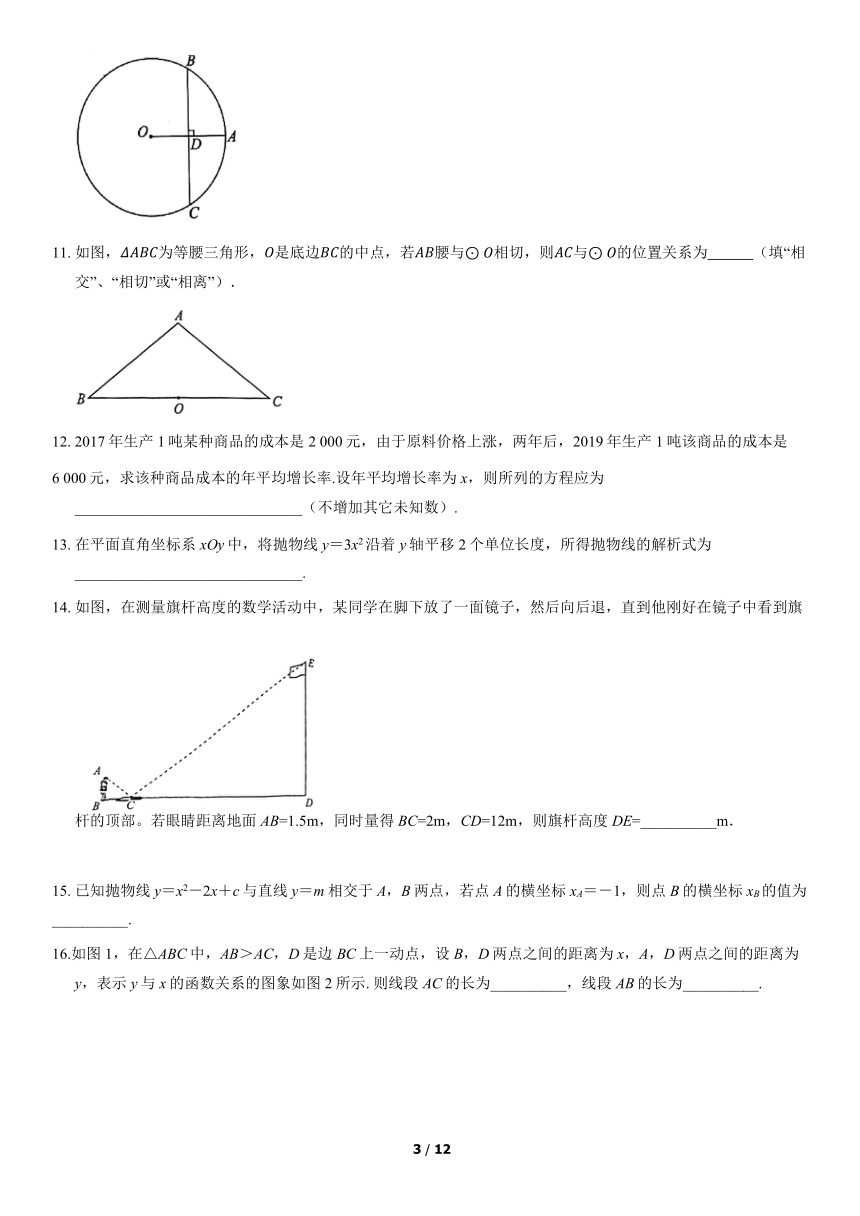
10. 如图,点A在⊙O上,弦BC垂直平分OA,垂足为D.若OA=4,则BC的长为__________.
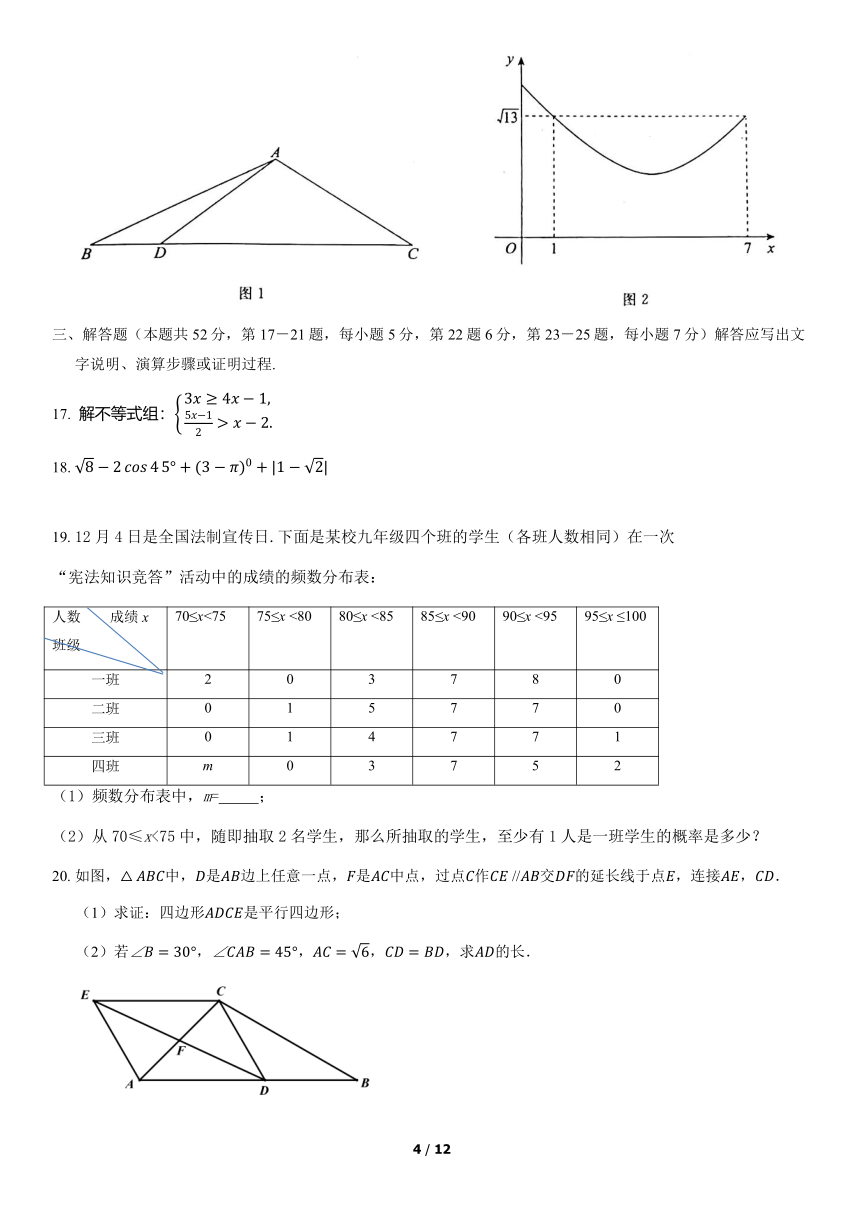
11. 如图,ΔABC为等腰三角形,O是底边BC的中点,若AB腰与⊙O相切,则AC与⊙O的位置关系为 (填“相交”、“相切”或“相离”).
12. 2017年生产1吨某种商品的成本是2 000元,由于原料价格上涨,两年后,2019年生产1吨该商品的成本是
6 000元,求该种商品成本的年平均增长率.设年平均增长率为x,则所列的方程应为______________________________(不增加其它未知数).
13. 在平面直角坐标系xOy中,将抛物线y=3x2沿着y轴平移2个单位长度,所得抛物线的解析式为______________________________.
33655052324014. 如图,在测量旗杆高度的数学活动中,某同学在脚下放了一面镜子,然后向后退,直到他刚好在镜子中看到旗杆的顶部。若眼睛距离地面AB=1.5m,同时量得BC=2m,CD=12m,则旗杆高度DE=__________m.
15. 已知抛物线y=x2-2x+c与直线y=m相交于A,B两点,若点A的横坐标xA=-1,则点B的横坐标xB的值为__________.
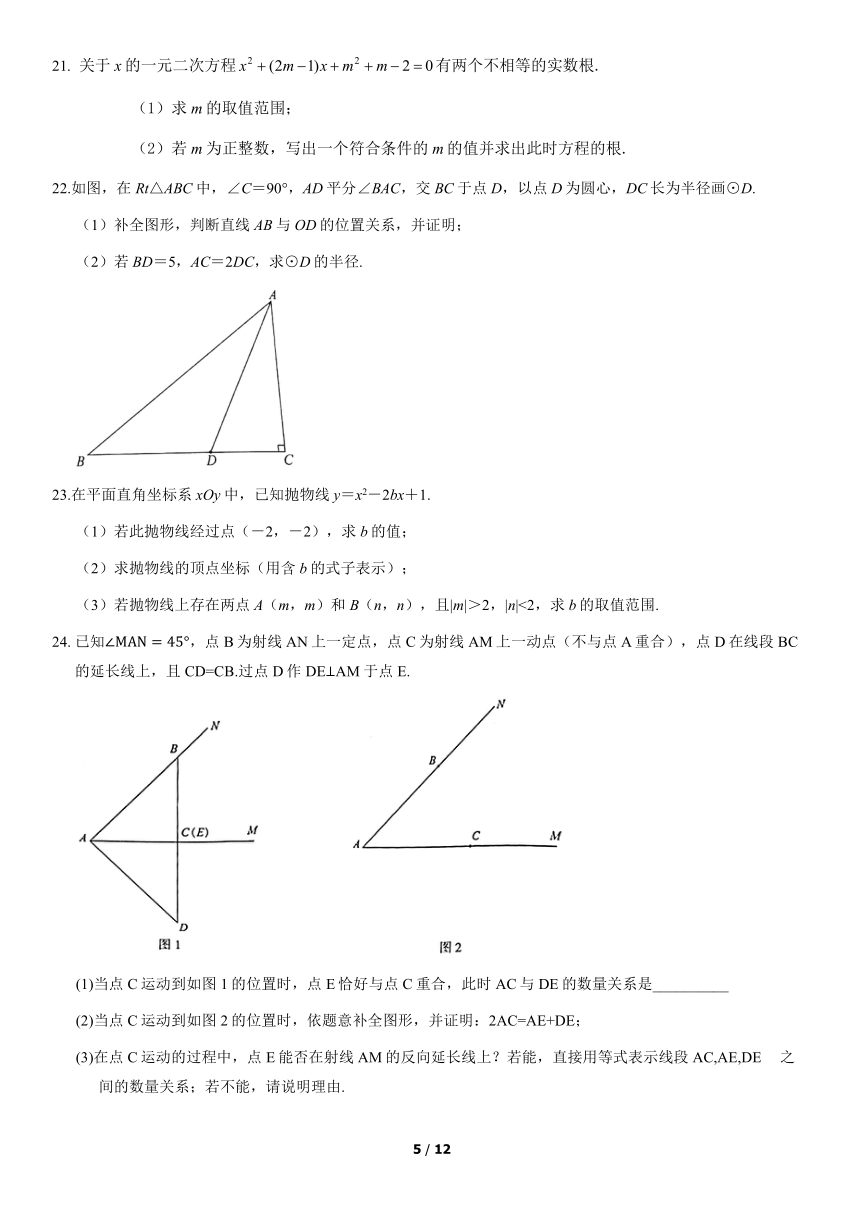
16.如图1,在△ABC中,AB>AC,D是边BC上一动点,设B,D两点之间的距离为x,A,D两点之间的距离为y,表示y与x的函数关系的图象如图2所示. 则线段AC的长为__________,线段AB的长为__________.
三、解答题(本题共52分,第17-21题,每小题5分,第22题6分,第23-25题,每小题7分)解答应写出文字说明、演算步骤或证明过程.
17. 解不等式组:&3x≥4x-1,&5x-12>x-2.
18. 8-2cos45°+(3-π)0+|1-2|
19. 12月4日是全国法制宣传日.下面是某校九年级四个班的学生(各班人数相同)在一次
“宪法知识竞答”活动中的成绩的频数分布表:
3105153810-70485270510人数 成绩x
班级
70≤x<75
75≤x <80
80≤x <85
85≤x <90
90≤x <95
95≤x ≤100
一班
2
0
3
7
8
0
二班
0
1
5
7
7
0
三班
0
1
4
7
7
1
四班
m
0
3
7
5
2
(1)频数分布表中,m= ;
(2)从70≤x<75中,随即抽取2名学生,那么所抽取的学生,至少有1人是一班学生的概率是多少?
20. 如图,△ABC中,D是AB边上任意一点,F是AC中点,过点C作CE //AB交DF的延长线于点E,连接AE,CD.
(1)求证:四边形ADCE是平行四边形;
(2)若∠B=30°,∠CAB=45°,AC=6,CD=BD,求AD的长.
21. 关于x的一元二次方程false有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为正整数,写出一个符合条件的m的值并求出此时方程的根.
22.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,以点D为圆心,DC长为半径画⊙D.
(1)补全图形,判断直线AB与OD的位置关系,并证明;
(2)若BD=5,AC=2DC,求⊙D的半径.
23.在平面直角坐标系xOy中,已知抛物线y=x2-2bx+1.
(1)若此抛物线经过点(-2,-2),求b的值;
(2)求抛物线的顶点坐标(用含b的式子表示);
(3)若抛物线上存在两点A(m,m)和B(n,n),且|m|>2,|n|<2,求b的取值范围.
24. 已知∠MAN=45°,点B为射线AN上一定点,点C为射线AM上一动点(不与点A重合),点D在线段BC的延长线上,且CD=CB.过点D作DE⊥AM于点E.
(1)当点C运动到如图1的位置时,点E恰好与点C重合,此时AC与DE的数量关系是__________
(2)当点C运动到如图2的位置时,依题意补全图形,并证明:2AC=AE+DE;
(3)在点C运动的过程中,点E能否在射线AM的反向延长线上?若能,直接用等式表示线段AC,AE,DE 之间的数量关系;若不能,请说明理由.
25.在平面直角坐标系xOy中,⊙O的半径为1.
给出如下定义:记线段AB的中点为M,当点M不在⊙O上时,平移线段AB,使点M落在⊙O上,得到线段A'B'(A',B'分别为点A,B的对应点).线段AA'长度的最小值称为线段AB到00的“平移距离”.
(1)已知点A的坐标为(-1,0),点B在x轴上.
①若点B与原点O重合,则线段AB到⊙O的“平移距离”为_____________;
②若线段AB到⊙O的“平移距离”为2,则点B的坐标为_____________;
(2)若点A,B都在直线y=43x+4上,且AB=2,记线段AB到⊙O的“平移距离”为d,求d1的最小值;
(3)若点A的坐标为(3,4),且AB=2,记线段AB到⊙O的“平移距离”为d2,直接写出d2的取值范围.
北京市第四十三中学初三数学摸底检测答案
一、选择题(本题共24分,每小题3分)
题号
1
2
3
4
5
6
7
8
答案
A
C
C
B
D
B
D
D
二、填空题(本题共24分,每小题3分)
9. 答案不唯一,如y=-x2 10. 43 11.相切
12. 20001+x2=6000 13. y=3x2+2 ,或y=3x2-2 14. 9
15. 3 16. 13,25
三.解答题(本题共52分,第17-21题,每小题5分,第22题6分,第23-25题,每小题7分)
17.-119.解:
(1) 3.
(2)一班有2人,分别记为A,B;四班有3人,分别记为C,D,E.
随即抽取2人的情况有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE.
至少有1人是一班的情况有AB,AC,AD,AE,BC,BD,BE
所以至少有1人是学生概率是710
20. (1)证明:∵false//false,2572385265430
falsefalse,
false.
∵false是false中点,
falsefalse.
falsefalse≌false.
falsefalse.
false四边形false是平行四边形.……………2分
(2)解:过点false作false于点false.
∵false,false,
falsefalse。
falsefalse.
在false中,false,false,false,
falsefalse.
在false中,false,false,false,
falsefalse.
falsefalse.……………5分
21.(1)由题意,false.
解得 false. ┈┈┈┈┈┈┈┈┈┈┈┈2分
(2)当m=1时,此时方程为false┈┈┈┈┈┈┈┈┈┈┈┈3分
∴方程的根为false. ┈┈┈┈┈┈┈┈┈┈┈┈5分
22. 解:(1)补全图形如图,直线AB与⊙D相切.┈┈┈┈┈┈┈┈┈┈┈┈1分
证明:作DE⊥AB于点E.
384810093345∵∠DCA=90°,AD是∠BAC的平分线,
∴DE=DC.┈┈┈┈┈┈┈┈┈┈┈┈┈2分
∴直线AB与⊙D相切.┈┈┈┈┈┈┈┈┈┈┈┈┈3分
(2)∵DE=DC,AC=2DC,
∴AC=2DE.
∵∠BCA=∠BED=90°,∠B=∠B,
∴?BCA∽?BED.┈┈┈┈┈┈┈┈┈┈┈┈┈4分
falseABDB=ACDE.
∴AB=2DB.
∵BD=5,
∴AB=10.┈┈┈┈┈┈┈┈┈┈┈┈┈5分
设DC=r,则AC=2r.
Rt?ABC中,BC2+AC2=AB2,
∴(5+r)2+(2r)2=102.
解得r=3.
∴⊙D的半径为3.┈┈┈┈┈┈┈┈┈┈┈┈┈6分
23.解:(1)∵抛物线经过点(-2,-2),
∴4+4b+1=-2.
∴b=-74. ┈┈┈┈┈┈┈┈┈┈┈2分
(2)抛物线的对称轴为直线x=b,纵坐标y=1-b2,顶点坐标b,1-b2.┈┈┈┈┈┈┈┈┈4分
(3)由(1)知,当抛物线经过点(-2,-2)时,b=-74.
当抛物线经过点(2,2)时,b=34.
①当b<-74时, 令x=-2,则y=4+4b+1=4b+5<-2;
令x=2, 则y=4-4b+1= -4b+5>2.
∵x>b时,y随着x的增大而增大,x<b时,y随着x的增大而减小,
∴b<-74符合题意;
②当b>34时, 令x=-2,则y=4+4b+1=4b+5>-2;
令x=2, 则y=4-4b+1= -4b+5<2.
∵x<b时,y随着x的增大而减小,x>b时,y随着x的增大而增大,
∴b>34符合题意;
③当-74≤b≤34时,令x=-2,则y=4+4b+1=4b+5≥-2;
令x=2, 则y=4-4b+1= -4b+5≥2.
∵抛物线的开口向上,
∴-74≤b≤34不符合题意.
综上所述,b的取值范围是b<-74,或b>34. ┈┈┈┈┈┈┈┈┈┈┈7分
24.解:(1)AC=DE; …………2分
(2)补全图形,
…………3分
证明:
354139544450法1:在射线AM上取点F,使AC=CF,
∵ AC=CF,BC=CD,∠BCA=∠DCF,
∴ △ABC≌△FDC.
∴ ∠DFE=∠A=45°.
∵ DE⊥AM,
∴ DE=EF.
∵ AF=AE+EF=2AC,
∴ 2AC=AE+DE. …………5分
法2:作BF⊥AM于点F,
∵ BF⊥AM,DE⊥AM,
∴ ∠BFC=∠DEC=90°.
∵ CD=CB,∠BCF=∠DCE,
∴ △BCF≌△DCE.
∴ CF=CE,BF=DE.
∵ ∠MAN=45°,
∴ AF=BF=DE.
∴ AE+DE=AF+FE+DE=2(AF+FC)=2AC. …………5分
结论得证.
(3)点E能在线段AC的反向延长线上,如图所示,此时2AC+AE=DE. …………7分
25. 解:(1)①线段AB到⊙O的“平移距离”为12. ┈┈┈┈┈┈┈┈┈┈1分
②B点的坐标为(-5,0)或(7,0). ┈┈┈┈┈┈┈┈┈┈┈3分
(2)如图,取AB的中点M,连接OM交⊙O于点M ',以M '为中点作线段A'B',使得A'B'∥AB且A'B’=AB =2,则四边形AA'BB' 为平行四边形.
∴M 'M=AA'. ┈┈┈┈┈┈┈┈┈┈┈4分
由题意可知,AA'=d1.
设直线y=43x+4交x轴于点C,交y轴于点D,
∴点C(-3,0),D(0,4).
∴CD=5.
过点O作ON⊥直线CD于点N,交⊙O于点N'.
在Rt△COD中,可得ON=125.
∴NN'=ON-ON'=125-1=75.
∵MM'≥NN',
∴MM'≥75.
∴AA'≥75.
∴d1的最小值是75 (当点M与点N重合时取得).┈┈┈┈┈┈┈┈┈┈┈5分
(3)3≤d2≤5. ┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈7分
数 学
考生须知
1.本试卷共8页,共三道大题,25道小题,满分100分,考试时间120分钟.
2.在试卷上和答题卡上准确填写学校、班级、姓名和教育ID号.
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.
4.在答题卡上选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答.
5.考试结束后,请将答题卡交回.
一、选择题(本题共24分,每小题3分)
第1-8题均有四个选项,符合题意的选项只有一个.
1. 已知反比例函数y=kx的图像经过点A(1,3),则k的值为
A.3 B.4
C.5 D.6
2. 下列图形中,既是中心对称图形又是轴对称图形的是
A.直角三角形 B.等边三角形
C. 圆 D.四边形
3. 若关于x的方程ax2-2ax+1=0的一个根是-1,则a的值是
A. 1 B. -1
C. -13 D. -3
4. 不透明袋子中有2个红球和2个绿球,这些球除颜色外无其他差别.从袋子中随机取出1个球,恰好是红球的概率为
13 B.12
5448300234315C.23 D.1
5. 如图,ΔABC中,点D,E分别在边AB,AC的反向延长线上,且DE//BC.若AE=2,AC=4,AD=3,则AB为
9 B. 32
C.3 D.6
6.如图,⊙O的内接正六边形ABCDEF的边长为1,则∩BC的长为
14π B.13π
C.23π D.π
7. 已知二次函数y=ax2+bx+c的部分图像如图所示,则使得函数值y大于2的自变量x的取值可以是
A.-4 B.2
C.0 D.-2
443865063508. 下列选项中,能够被半径为1的圆及其内部所覆盖的图形是
A.长度为5的线段 B.斜边为3的直角三角形
C.面积为4的菱形 D.半径为2,圆心角为90?的扇形
二、填空题(本题共24分,每小题3分)
9. 写出一个二次函数,使其满足:①图象开口向下;②当x<0时,y随着x的增大而增大.这个二次函数的解析式可以是_______________.
10. 如图,点A在⊙O上,弦BC垂直平分OA,垂足为D.若OA=4,则BC的长为__________.
11. 如图,ΔABC为等腰三角形,O是底边BC的中点,若AB腰与⊙O相切,则AC与⊙O的位置关系为 (填“相交”、“相切”或“相离”).
12. 2017年生产1吨某种商品的成本是2 000元,由于原料价格上涨,两年后,2019年生产1吨该商品的成本是
6 000元,求该种商品成本的年平均增长率.设年平均增长率为x,则所列的方程应为______________________________(不增加其它未知数).
13. 在平面直角坐标系xOy中,将抛物线y=3x2沿着y轴平移2个单位长度,所得抛物线的解析式为______________________________.
33655052324014. 如图,在测量旗杆高度的数学活动中,某同学在脚下放了一面镜子,然后向后退,直到他刚好在镜子中看到旗杆的顶部。若眼睛距离地面AB=1.5m,同时量得BC=2m,CD=12m,则旗杆高度DE=__________m.
15. 已知抛物线y=x2-2x+c与直线y=m相交于A,B两点,若点A的横坐标xA=-1,则点B的横坐标xB的值为__________.
16.如图1,在△ABC中,AB>AC,D是边BC上一动点,设B,D两点之间的距离为x,A,D两点之间的距离为y,表示y与x的函数关系的图象如图2所示. 则线段AC的长为__________,线段AB的长为__________.
三、解答题(本题共52分,第17-21题,每小题5分,第22题6分,第23-25题,每小题7分)解答应写出文字说明、演算步骤或证明过程.
17. 解不等式组:&3x≥4x-1,&5x-12>x-2.
18. 8-2cos45°+(3-π)0+|1-2|
19. 12月4日是全国法制宣传日.下面是某校九年级四个班的学生(各班人数相同)在一次
“宪法知识竞答”活动中的成绩的频数分布表:
3105153810-70485270510人数 成绩x
班级
70≤x<75
75≤x <80
80≤x <85
85≤x <90
90≤x <95
95≤x ≤100
一班
2
0
3
7
8
0
二班
0
1
5
7
7
0
三班
0
1
4
7
7
1
四班
m
0
3
7
5
2
(1)频数分布表中,m= ;
(2)从70≤x<75中,随即抽取2名学生,那么所抽取的学生,至少有1人是一班学生的概率是多少?
20. 如图,△ABC中,D是AB边上任意一点,F是AC中点,过点C作CE //AB交DF的延长线于点E,连接AE,CD.
(1)求证:四边形ADCE是平行四边形;
(2)若∠B=30°,∠CAB=45°,AC=6,CD=BD,求AD的长.
21. 关于x的一元二次方程false有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为正整数,写出一个符合条件的m的值并求出此时方程的根.
22.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,以点D为圆心,DC长为半径画⊙D.
(1)补全图形,判断直线AB与OD的位置关系,并证明;
(2)若BD=5,AC=2DC,求⊙D的半径.
23.在平面直角坐标系xOy中,已知抛物线y=x2-2bx+1.
(1)若此抛物线经过点(-2,-2),求b的值;
(2)求抛物线的顶点坐标(用含b的式子表示);
(3)若抛物线上存在两点A(m,m)和B(n,n),且|m|>2,|n|<2,求b的取值范围.
24. 已知∠MAN=45°,点B为射线AN上一定点,点C为射线AM上一动点(不与点A重合),点D在线段BC的延长线上,且CD=CB.过点D作DE⊥AM于点E.
(1)当点C运动到如图1的位置时,点E恰好与点C重合,此时AC与DE的数量关系是__________
(2)当点C运动到如图2的位置时,依题意补全图形,并证明:2AC=AE+DE;
(3)在点C运动的过程中,点E能否在射线AM的反向延长线上?若能,直接用等式表示线段AC,AE,DE 之间的数量关系;若不能,请说明理由.
25.在平面直角坐标系xOy中,⊙O的半径为1.
给出如下定义:记线段AB的中点为M,当点M不在⊙O上时,平移线段AB,使点M落在⊙O上,得到线段A'B'(A',B'分别为点A,B的对应点).线段AA'长度的最小值称为线段AB到00的“平移距离”.
(1)已知点A的坐标为(-1,0),点B在x轴上.
①若点B与原点O重合,则线段AB到⊙O的“平移距离”为_____________;
②若线段AB到⊙O的“平移距离”为2,则点B的坐标为_____________;
(2)若点A,B都在直线y=43x+4上,且AB=2,记线段AB到⊙O的“平移距离”为d,求d1的最小值;
(3)若点A的坐标为(3,4),且AB=2,记线段AB到⊙O的“平移距离”为d2,直接写出d2的取值范围.
北京市第四十三中学初三数学摸底检测答案
一、选择题(本题共24分,每小题3分)
题号
1
2
3
4
5
6
7
8
答案
A
C
C
B
D
B
D
D
二、填空题(本题共24分,每小题3分)
9. 答案不唯一,如y=-x2 10. 43 11.相切
12. 20001+x2=6000 13. y=3x2+2 ,或y=3x2-2 14. 9
15. 3 16. 13,25
三.解答题(本题共52分,第17-21题,每小题5分,第22题6分,第23-25题,每小题7分)
17.-1
(1) 3.
(2)一班有2人,分别记为A,B;四班有3人,分别记为C,D,E.
随即抽取2人的情况有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE.
至少有1人是一班的情况有AB,AC,AD,AE,BC,BD,BE
所以至少有1人是学生概率是710
20. (1)证明:∵false//false,2572385265430
falsefalse,
false.
∵false是false中点,
falsefalse.
falsefalse≌false.
falsefalse.
false四边形false是平行四边形.……………2分
(2)解:过点false作false于点false.
∵false,false,
falsefalse。
falsefalse.
在false中,false,false,false,
falsefalse.
在false中,false,false,false,
falsefalse.
falsefalse.……………5分
21.(1)由题意,false.
解得 false. ┈┈┈┈┈┈┈┈┈┈┈┈2分
(2)当m=1时,此时方程为false┈┈┈┈┈┈┈┈┈┈┈┈3分
∴方程的根为false. ┈┈┈┈┈┈┈┈┈┈┈┈5分
22. 解:(1)补全图形如图,直线AB与⊙D相切.┈┈┈┈┈┈┈┈┈┈┈┈1分
证明:作DE⊥AB于点E.
384810093345∵∠DCA=90°,AD是∠BAC的平分线,
∴DE=DC.┈┈┈┈┈┈┈┈┈┈┈┈┈2分
∴直线AB与⊙D相切.┈┈┈┈┈┈┈┈┈┈┈┈┈3分
(2)∵DE=DC,AC=2DC,
∴AC=2DE.
∵∠BCA=∠BED=90°,∠B=∠B,
∴?BCA∽?BED.┈┈┈┈┈┈┈┈┈┈┈┈┈4分
falseABDB=ACDE.
∴AB=2DB.
∵BD=5,
∴AB=10.┈┈┈┈┈┈┈┈┈┈┈┈┈5分
设DC=r,则AC=2r.
Rt?ABC中,BC2+AC2=AB2,
∴(5+r)2+(2r)2=102.
解得r=3.
∴⊙D的半径为3.┈┈┈┈┈┈┈┈┈┈┈┈┈6分
23.解:(1)∵抛物线经过点(-2,-2),
∴4+4b+1=-2.
∴b=-74. ┈┈┈┈┈┈┈┈┈┈┈2分
(2)抛物线的对称轴为直线x=b,纵坐标y=1-b2,顶点坐标b,1-b2.┈┈┈┈┈┈┈┈┈4分
(3)由(1)知,当抛物线经过点(-2,-2)时,b=-74.
当抛物线经过点(2,2)时,b=34.
①当b<-74时, 令x=-2,则y=4+4b+1=4b+5<-2;
令x=2, 则y=4-4b+1= -4b+5>2.
∵x>b时,y随着x的增大而增大,x<b时,y随着x的增大而减小,
∴b<-74符合题意;
②当b>34时, 令x=-2,则y=4+4b+1=4b+5>-2;
令x=2, 则y=4-4b+1= -4b+5<2.
∵x<b时,y随着x的增大而减小,x>b时,y随着x的增大而增大,
∴b>34符合题意;
③当-74≤b≤34时,令x=-2,则y=4+4b+1=4b+5≥-2;
令x=2, 则y=4-4b+1= -4b+5≥2.
∵抛物线的开口向上,
∴-74≤b≤34不符合题意.
综上所述,b的取值范围是b<-74,或b>34. ┈┈┈┈┈┈┈┈┈┈┈7分
24.解:(1)AC=DE; …………2分
(2)补全图形,
…………3分
证明:
354139544450法1:在射线AM上取点F,使AC=CF,
∵ AC=CF,BC=CD,∠BCA=∠DCF,
∴ △ABC≌△FDC.
∴ ∠DFE=∠A=45°.
∵ DE⊥AM,
∴ DE=EF.
∵ AF=AE+EF=2AC,
∴ 2AC=AE+DE. …………5分
法2:作BF⊥AM于点F,
∵ BF⊥AM,DE⊥AM,
∴ ∠BFC=∠DEC=90°.
∵ CD=CB,∠BCF=∠DCE,
∴ △BCF≌△DCE.
∴ CF=CE,BF=DE.
∵ ∠MAN=45°,
∴ AF=BF=DE.
∴ AE+DE=AF+FE+DE=2(AF+FC)=2AC. …………5分
结论得证.
(3)点E能在线段AC的反向延长线上,如图所示,此时2AC+AE=DE. …………7分
25. 解:(1)①线段AB到⊙O的“平移距离”为12. ┈┈┈┈┈┈┈┈┈┈1分
②B点的坐标为(-5,0)或(7,0). ┈┈┈┈┈┈┈┈┈┈┈3分
(2)如图,取AB的中点M,连接OM交⊙O于点M ',以M '为中点作线段A'B',使得A'B'∥AB且A'B’=AB =2,则四边形AA'BB' 为平行四边形.
∴M 'M=AA'. ┈┈┈┈┈┈┈┈┈┈┈4分
由题意可知,AA'=d1.
设直线y=43x+4交x轴于点C,交y轴于点D,
∴点C(-3,0),D(0,4).
∴CD=5.
过点O作ON⊥直线CD于点N,交⊙O于点N'.
在Rt△COD中,可得ON=125.
∴NN'=ON-ON'=125-1=75.
∵MM'≥NN',
∴MM'≥75.
∴AA'≥75.
∴d1的最小值是75 (当点M与点N重合时取得).┈┈┈┈┈┈┈┈┈┈┈5分
(3)3≤d2≤5. ┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈┈7分
同课章节目录
