四川省资阳市11-12学年高二上学期期末质量检测(数学文)
文档属性
| 名称 | 四川省资阳市11-12学年高二上学期期末质量检测(数学文) |
|
|
| 格式 | zip | ||
| 文件大小 | 261.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-30 00:00:00 | ||
图片预览





文档简介
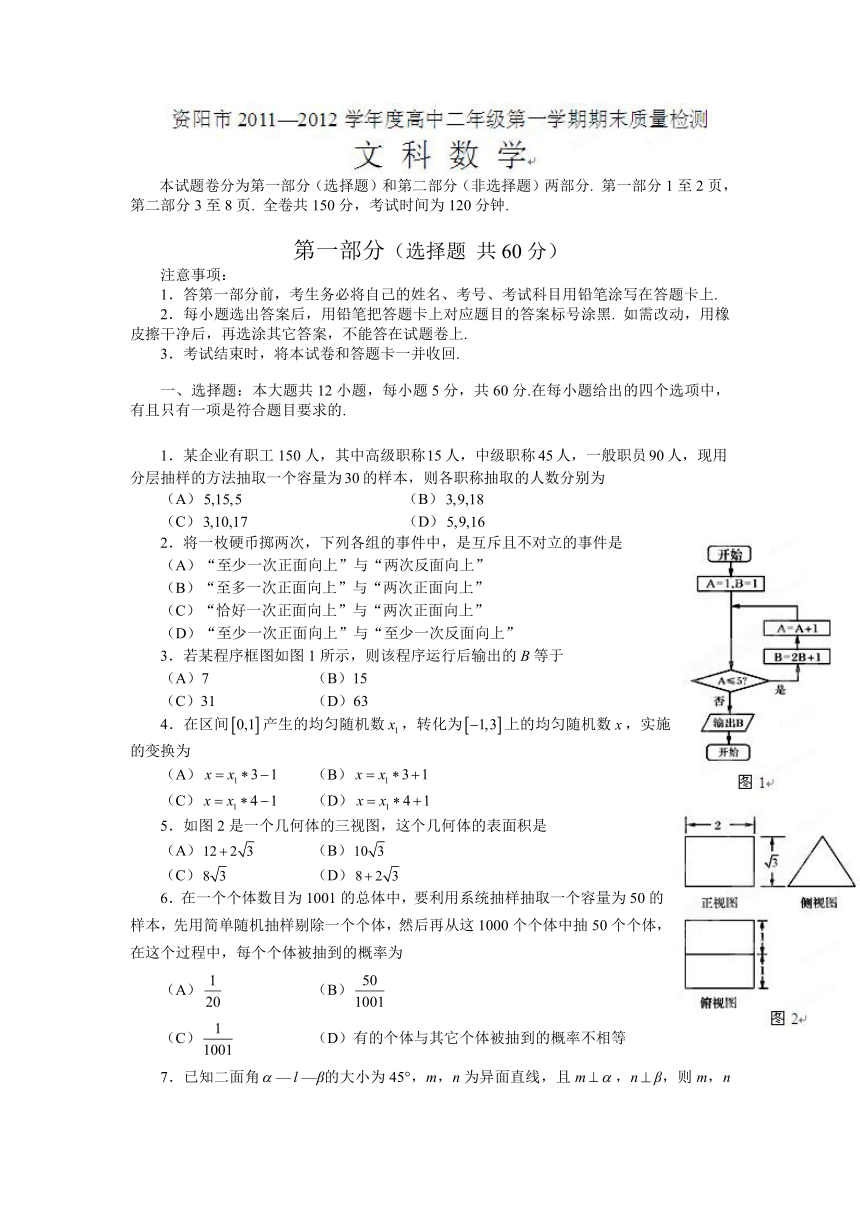
本试题卷分为第一部分(选择题)和第二部分(非选择题)两部分. 第一部分1至2页,第二部分3至8页. 全卷共150分,考试时间为120分钟.
第一部分(选择题 共60分)
注意事项:
1.答第一部分前,考生务必将自己的姓名、考号、考试科目用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑. 如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.
3.考试结束时,将本试卷和答题卡一并收回.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的.
1.某企业有职工150人,其中高级职称人,中级职称人,一般职员人,现用分层抽样的方法抽取一个容量为的样本,则各职称抽取的人数分别为
(A) (B)
(C) (D)
2.将一枚硬币掷两次,下列各组的事件中,是互斥且不对立的事件是
(A)“至少一次正面向上”与“两次反面向上”
(B)“至多一次正面向上”与“两次正面向上”
(C)“恰好一次正面向上”与“两次正面向上”
(D)“至少一次正面向上”与“至少一次反面向上”
3.若某程序框图如图1所示,则该程序运行后输出的B等于
(A)7 (B)15
(C)31 (D)63
4.在区间产生的均匀随机数,转化为上的均匀随机数,实施的变换为
(A) (B)
(C) (D)
5.如图2是一个几何体的三视图,这个几何体的表面积是
(A) (B)
(C) (D)
6.在一个个体数目为1001的总体中,要利用系统抽样抽取一个容量为50的样本,先用简单随机抽样剔除一个个体,然后再从这1000个个体中抽50个个体,在这个过程中,每个个体被抽到的概率为
(A) (B)
(C) (D)有的个体与其它个体被抽到的概率不相等
7.已知二面角——β的大小为45°,m,n为异面直线,且m,nβ,则m,n所成角的大小为
(A)135° (B)90° (C)60° (D)45°
8.某人午觉醒来,发现表停了,他打开收音机,想听电台报时,则他等待的时间不多于15分钟的概率是
(A) (B) (C) (D)
9.若直线平行于平面内的无数条直线,则下列结论正确的是
(A) (B)
(C) (D)
10.执行如图3所示的程序框图,若要使输入的与输出的的值相等,则的可能值的个数为
(A)1 (B)2
(C)3 (D)4
11.已知a、b、c是三条不同的直线,、、是三个不同的平面,则下列命题正确的是
(A), a∥b (B)a∥,b∥a∥b
(C), ∥ (D)∥,∥∥
12.已知长方体的长、宽、高分别为3、4、5,在与一条棱平行的截面中,最大截面面积为
(A)25 (B)20 (C) (D)
二、填空题:本大题共4小题,每小题4分,共16分.把答案直接填在题中横线上.
13.已知球半径,则它的体积_________.
14.设有一个线性回归方程为,当变量x增加一个单位时,y的值平均增加_______.
15.输入,运行右面的程序之后得到的结果为_____.
16.如图4,点P在正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列四个命题:
①直线AD与直线B1P为异面直线;
②A1P∥面ACD1;
③三棱锥A-D1PC的体积为定值;
④面PDB1⊥面ACD1.
其中所有正确命题的序号是 .
三、解答题:本大题共6个小题,共74分.解答要写出文字说明,证明过程或演算步骤.
17. (本小题满分12分)
甲 乙
9 8 2 1 0 0 12 7 8 90 3 3
甲、乙两人同时生产一种产品,6天中,完成的产量茎叶图(茎表示十位,叶表示个位)如图所示:
(Ⅰ)写出甲、乙的众数和中位数;
(Ⅱ)计算甲、乙的平均数和方差,依此判断谁更优秀?
18. (本小题满分12分)
如图5,已知平面∩平面=AB,PQ⊥于Q,PC⊥于C,CD⊥于D,
(Ⅰ)求证:P、C、D、Q四点共面;
(Ⅱ)求证:QD⊥AB.
19. (本小题满分12分)
甲、乙两人各掷一颗质地均匀的骰子,如果所得它们向上的点数之和为偶数,则甲赢,否则乙赢.
(Ⅰ)求两个骰子向上点数之和为8的事件发生的概率;
(Ⅱ)这种游戏规则公平吗?试说明理由.
20. (本小题满分12分)
如图6,在三棱柱中,△ABC为等边三角形,侧棱⊥平面,,D、E分别为、的中点.
(Ⅰ)求证:DE⊥平面;
(Ⅱ)求BC与平面所成角;
(Ⅲ)求三棱锥的体积.
21. (本小题满分12分)
某班50名学生在一次数学考试中,成绩都属于区间[60,110],将成绩按如下方式分成五组:第一组[60,70);第二组[70,80);第三组[80,90);第四组[90,100);第五组[100,110],部分频率分布直方图如图7所示.
(Ⅰ)请补全频率分布直方图;
(Ⅱ)由此估计该班的平均分;
(Ⅲ)在成绩属于[60,70)∪[100,110]的学生中任取两人,成绩记为,求的概率.
22. (本小题满分14分)
如图8所示,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的倍,点P在侧棱SD上,且.
(Ⅰ)求证:AC⊥SD;
(Ⅱ)点E在SC上,且,求证:BE∥平面PAC;
(Ⅲ)求二面角P-AC-D的大小.
资阳市2011—2012学年度高中二年级第一学期期末质量检测
文科数学参考答案及评分意见
一、选择题:本大题共12个小题,每小题5分,共60分.
1-5.BCDCA;6-10. BDCDC;11-12.DA
二、填空题:本大题共4个小题,每小题4分,共16分.
13. ;14. 1.5;15.3;16. ②③④.
三、解答题:本大题共6个小题,共74分.
18.(Ⅰ)∵PQ⊥,CD⊥,∴PQ∥CD,
于是P、C、D、Q四点共面于; 6分
(Ⅱ)∵AB,∴PQ⊥AB,
又∵PC⊥,AB,∴PC⊥AB,
又∵PQ∩PC=P,∴AB⊥,
又∵QD,∴AB⊥QD. 12分
(Ⅱ)这种游戏规则是公平的 7分
设甲胜为事件B,乙胜为事件C,则甲胜即两个骰子点数之和为偶数所包含的基本事件数有18个:(1,1),(1,3),(1,5),(2,2),(2,4),(2,6),(3,1),(3,3),(3,5),(4,2),(4,4),(4,6),(5,1),(5,3),(5,5),(6,2),(6,4),(6,6). 9分
所以甲胜的概率,乙胜的概率= 11分
所以这种游戏规则是公平的. 12分
20.(Ⅰ)设中点为F,连结AF,EF,,
而,四边形为平行四边形,
,
4分
(Ⅱ)由(Ⅰ)可得, ,过,
,
8分
(Ⅲ) 12分
21.(Ⅰ)由图得,成绩在[60,70),[70,80),[80,90),[100,110]的频率分别为0.06,0.16,0.38,0.08,所以在的频率为. 3分
补全的频率分布直方图如图所示. 4分
(Ⅱ)估计该班的平均分为
8分
(Ⅲ)由题得:成绩在的有3人,设编号为1,2,3,在的为4人.设编号为4,5,6,7,基本事件有:(1,2),(1,3),(1,4),(1,5),(1,6),(1,7),(2,3),(2,4),(2,5),(2,6),(2,7),(3,4),(3,5),(3,6),(3,7),(4,5),(4,6),(4,7),(5,6),(5,7),(6,7)共21个,满足的事件有(1,4),(1,5),(1,6),(1,7),(2,4),(2,5),(2, 6),(2,7),(3,4),(3,5),(3,6),(3,7)共12个 10分所以的概率为. 12分
(Ⅲ)设正方形ABCD的边长为a,则,又,
∴,又OP平面SBD,由(Ⅰ)知AC⊥平面SBD,
∴AC⊥OP,且AC⊥OD,
∴是二面角P-AC-D的平面角. 12分
△POD中,,,
,则,
∴△POD是Rt△,又,∴.
∴二面角P-AC-D的大小. 14分
版权所有:高考资源网(www.)
图3
第一部分(选择题 共60分)
注意事项:
1.答第一部分前,考生务必将自己的姓名、考号、考试科目用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑. 如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.
3.考试结束时,将本试卷和答题卡一并收回.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的.
1.某企业有职工150人,其中高级职称人,中级职称人,一般职员人,现用分层抽样的方法抽取一个容量为的样本,则各职称抽取的人数分别为
(A) (B)
(C) (D)
2.将一枚硬币掷两次,下列各组的事件中,是互斥且不对立的事件是
(A)“至少一次正面向上”与“两次反面向上”
(B)“至多一次正面向上”与“两次正面向上”
(C)“恰好一次正面向上”与“两次正面向上”
(D)“至少一次正面向上”与“至少一次反面向上”
3.若某程序框图如图1所示,则该程序运行后输出的B等于
(A)7 (B)15
(C)31 (D)63
4.在区间产生的均匀随机数,转化为上的均匀随机数,实施的变换为
(A) (B)
(C) (D)
5.如图2是一个几何体的三视图,这个几何体的表面积是
(A) (B)
(C) (D)
6.在一个个体数目为1001的总体中,要利用系统抽样抽取一个容量为50的样本,先用简单随机抽样剔除一个个体,然后再从这1000个个体中抽50个个体,在这个过程中,每个个体被抽到的概率为
(A) (B)
(C) (D)有的个体与其它个体被抽到的概率不相等
7.已知二面角——β的大小为45°,m,n为异面直线,且m,nβ,则m,n所成角的大小为
(A)135° (B)90° (C)60° (D)45°
8.某人午觉醒来,发现表停了,他打开收音机,想听电台报时,则他等待的时间不多于15分钟的概率是
(A) (B) (C) (D)
9.若直线平行于平面内的无数条直线,则下列结论正确的是
(A) (B)
(C) (D)
10.执行如图3所示的程序框图,若要使输入的与输出的的值相等,则的可能值的个数为
(A)1 (B)2
(C)3 (D)4
11.已知a、b、c是三条不同的直线,、、是三个不同的平面,则下列命题正确的是
(A), a∥b (B)a∥,b∥a∥b
(C), ∥ (D)∥,∥∥
12.已知长方体的长、宽、高分别为3、4、5,在与一条棱平行的截面中,最大截面面积为
(A)25 (B)20 (C) (D)
二、填空题:本大题共4小题,每小题4分,共16分.把答案直接填在题中横线上.
13.已知球半径,则它的体积_________.
14.设有一个线性回归方程为,当变量x增加一个单位时,y的值平均增加_______.
15.输入,运行右面的程序之后得到的结果为_____.
16.如图4,点P在正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列四个命题:
①直线AD与直线B1P为异面直线;
②A1P∥面ACD1;
③三棱锥A-D1PC的体积为定值;
④面PDB1⊥面ACD1.
其中所有正确命题的序号是 .
三、解答题:本大题共6个小题,共74分.解答要写出文字说明,证明过程或演算步骤.
17. (本小题满分12分)
甲 乙
9 8 2 1 0 0 12 7 8 90 3 3
甲、乙两人同时生产一种产品,6天中,完成的产量茎叶图(茎表示十位,叶表示个位)如图所示:
(Ⅰ)写出甲、乙的众数和中位数;
(Ⅱ)计算甲、乙的平均数和方差,依此判断谁更优秀?
18. (本小题满分12分)
如图5,已知平面∩平面=AB,PQ⊥于Q,PC⊥于C,CD⊥于D,
(Ⅰ)求证:P、C、D、Q四点共面;
(Ⅱ)求证:QD⊥AB.
19. (本小题满分12分)
甲、乙两人各掷一颗质地均匀的骰子,如果所得它们向上的点数之和为偶数,则甲赢,否则乙赢.
(Ⅰ)求两个骰子向上点数之和为8的事件发生的概率;
(Ⅱ)这种游戏规则公平吗?试说明理由.
20. (本小题满分12分)
如图6,在三棱柱中,△ABC为等边三角形,侧棱⊥平面,,D、E分别为、的中点.
(Ⅰ)求证:DE⊥平面;
(Ⅱ)求BC与平面所成角;
(Ⅲ)求三棱锥的体积.
21. (本小题满分12分)
某班50名学生在一次数学考试中,成绩都属于区间[60,110],将成绩按如下方式分成五组:第一组[60,70);第二组[70,80);第三组[80,90);第四组[90,100);第五组[100,110],部分频率分布直方图如图7所示.
(Ⅰ)请补全频率分布直方图;
(Ⅱ)由此估计该班的平均分;
(Ⅲ)在成绩属于[60,70)∪[100,110]的学生中任取两人,成绩记为,求的概率.
22. (本小题满分14分)
如图8所示,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的倍,点P在侧棱SD上,且.
(Ⅰ)求证:AC⊥SD;
(Ⅱ)点E在SC上,且,求证:BE∥平面PAC;
(Ⅲ)求二面角P-AC-D的大小.
资阳市2011—2012学年度高中二年级第一学期期末质量检测
文科数学参考答案及评分意见
一、选择题:本大题共12个小题,每小题5分,共60分.
1-5.BCDCA;6-10. BDCDC;11-12.DA
二、填空题:本大题共4个小题,每小题4分,共16分.
13. ;14. 1.5;15.3;16. ②③④.
三、解答题:本大题共6个小题,共74分.
18.(Ⅰ)∵PQ⊥,CD⊥,∴PQ∥CD,
于是P、C、D、Q四点共面于; 6分
(Ⅱ)∵AB,∴PQ⊥AB,
又∵PC⊥,AB,∴PC⊥AB,
又∵PQ∩PC=P,∴AB⊥,
又∵QD,∴AB⊥QD. 12分
(Ⅱ)这种游戏规则是公平的 7分
设甲胜为事件B,乙胜为事件C,则甲胜即两个骰子点数之和为偶数所包含的基本事件数有18个:(1,1),(1,3),(1,5),(2,2),(2,4),(2,6),(3,1),(3,3),(3,5),(4,2),(4,4),(4,6),(5,1),(5,3),(5,5),(6,2),(6,4),(6,6). 9分
所以甲胜的概率,乙胜的概率= 11分
所以这种游戏规则是公平的. 12分
20.(Ⅰ)设中点为F,连结AF,EF,,
而,四边形为平行四边形,
,
4分
(Ⅱ)由(Ⅰ)可得, ,过,
,
8分
(Ⅲ) 12分
21.(Ⅰ)由图得,成绩在[60,70),[70,80),[80,90),[100,110]的频率分别为0.06,0.16,0.38,0.08,所以在的频率为. 3分
补全的频率分布直方图如图所示. 4分
(Ⅱ)估计该班的平均分为
8分
(Ⅲ)由题得:成绩在的有3人,设编号为1,2,3,在的为4人.设编号为4,5,6,7,基本事件有:(1,2),(1,3),(1,4),(1,5),(1,6),(1,7),(2,3),(2,4),(2,5),(2,6),(2,7),(3,4),(3,5),(3,6),(3,7),(4,5),(4,6),(4,7),(5,6),(5,7),(6,7)共21个,满足的事件有(1,4),(1,5),(1,6),(1,7),(2,4),(2,5),(2, 6),(2,7),(3,4),(3,5),(3,6),(3,7)共12个 10分所以的概率为. 12分
(Ⅲ)设正方形ABCD的边长为a,则,又,
∴,又OP平面SBD,由(Ⅰ)知AC⊥平面SBD,
∴AC⊥OP,且AC⊥OD,
∴是二面角P-AC-D的平面角. 12分
△POD中,,,
,则,
∴△POD是Rt△,又,∴.
∴二面角P-AC-D的大小. 14分
版权所有:高考资源网(www.)
图3
同课章节目录
