人教版(2019)高考物理三轮冲刺专题复习 专题06几何方法课件(17张PPT)
文档属性
| 名称 | 人教版(2019)高考物理三轮冲刺专题复习 专题06几何方法课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-24 00:00:00 | ||
图片预览






文档简介
专题06 几何方法
2021年高考物理三轮复习解题方法专题
方法概述
01
物理问题通常都配有一个与真实的物理情境相对应的示意图形,在对研究对象进行受力分析、描画轨迹、分解速度、描绘光路时,会形成各种各样的几何形状,分析求解时经常要用到几何方法——相似三角形法、几何作图法.
02
相似三角形法
一、相似三角形法
在共点力平衡问题、运动的合成和分解、电磁场的合成和分解以及几何光学等物理情境中,常会出现力三角形、速度三角形、位移三角形等矢量三角形和结构(长度)三角形相似的情况,准确作图、仔细观察、灵活选用相似三角形的边角关系是解题的关键.
相似三角形的一些性质:①对应角相等;②对应边成比例;③对应的垂线、中线、角平分线成比例.
圆的几何知识及应用
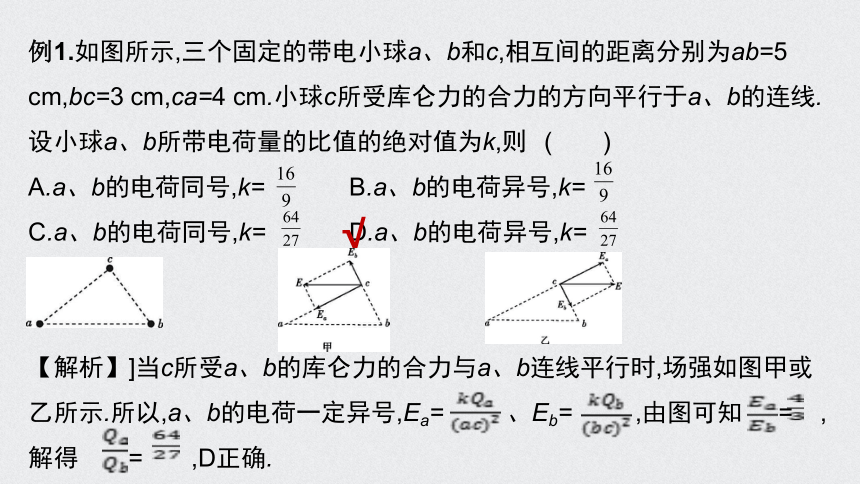
例1.如图所示,三个固定的带电小球a、b和c,相互间的距离分别为ab=5 cm,bc=3 cm,ca=4 cm.小球c所受库仑力的合力的方向平行于a、b的连线.设小球a、b所带电荷量的比值的绝对值为k,则 ( )
A.a、b的电荷同号,k= B.a、b的电荷异号,k=
C.a、b的电荷同号,k= D.a、b的电荷异号,k=
?
?
【解析】]当c所受a、b的库仑力的合力与a、b连线平行时,场强如图甲或乙所示.所以,a、b的电荷一定异号,Ea= 、Eb= ,由图可知 = ,解得 = ,D正确.
√
变式训练1 如图所示,两球A、B用劲度系数为k1的轻弹簧相连,球B用长为L的细绳悬于O点,球A固定在O点正下方,且点O、A之间的距离恰为L,系统平衡时绳子所受的拉力为F1.现把A、B间的弹簧换成劲度系数为k2的轻弹(k2>k1),仍使系统平衡,此时绳子所受拉力为F2,则F1与F2的大小关系为( )
A.F1>F2 B.F1=F2
C.F1√
【解析】 以小球B为研究对象分析受力情况,小球B受到重力、细绳拉力F和弹簧弹力FN的作用处于平衡状态,由共点力的平衡条件可知,弹簧的弹力FN和绳子的拉力F的合力F合与重力mg大小相等,方向相反,作出小球B的受力图,由于三角形OAB与三角形BCD相似,故有 = ,由于OA=OB=L,F合=mg,故绳子的拉力F与弹簧的弹力无关即与弹簧劲度系数无关,只与小球所受重力有关,即有F1=F2,故B正确,A、C、D错误.
例2 一条宽为L的河流,水流速度为 u,船在静水中划行的速度为v ,且 。要使船到达对岸的位移最短,船的航向如何?最短位移多大?
解析:水流速度 u、船在静水中的速度v 与船的合速度 构成一矢量三角形,且船在静水中的速度 大小不变,方向不定,构建如图1所示的矢量圆。显然,当AD与矢量圆相切时,船航行的位移最短。由图可得船的航向与河岸的夹角 由相似三角形得
最短位移
二、几何作图法
我们先看弦轨道模型问题并证明物体下滑的等时性。
如图所示,让物体从竖直圆环上的最高点A处由静止开始沿光滑的弦轨道AB 、AC、AD下滑(AD竖直),下滑的时间分别为 、 、 。试证明
证明:物体由静止开始沿AB弦轨道下滑,AB弦轨道长为 ,AB弦轨道与竖直方向夹角为 ,直径AD长为 。
①
②
③
①②③解得:
可知物体由静止开始沿光滑弦轨道下滑的时间与弦与竖直方向的夹角无关,即
(1)质点在竖直圆环上沿不同的光滑弦从其上端由静止开始滑到环的最低点所用时间相等,如图甲所示。
(2)质点从竖直圆环上最高点沿不同的光滑弦由静止开始滑到下端所用时间相等,如图乙所示。
依据弦轨道等时性特点,可以用作图的方法解题
例3 在倾角为θ的斜面上方的A点放置一光滑的木板AB,B端刚好在斜面上,木板与竖直方向所成角度为α,一小物块由A端沿木板由静止下滑,要使物块滑到斜面的时间最短,则α与θ角的大小关系为( )。
A.α=θ B.α= C.α=2θ D.α=
【解析】作法:过A点作竖直线AB,过A作水平线与斜面交Q点,作 的角平分线与AB交于O点,以O点为圆心、AO长为半径作圆切斜面于P点,AP径迹即为最短时间。∠POB=θ,则α= ,B项正确。
√
变式训练2 如图所示,在竖直平面内建立直角坐标系xOy,该平面内有AM、BM、CM三条光滑固定轨道,其中AM=MCA.tAC.tA=tC=tB
D.无法比较时间大小关系
解析 作三角形MBC外接圆,由弦轨道等时性特点得出 tA=tC√
变式训练3 为了使雨滴能尽快地淌离房顶,要设计好房顶的高度(围墙已建好),设雨滴沿房顶下淌时做无初速度无摩擦的运动,那么如图所示的四种情况符合要求的是( C )
解析 以横梁的中点M为圆心,以横梁长度的二分之一为半径画圆,由弦轨道的等时性可以得出45度角的房顶,雨滴下滑时间最短。
?
?
?
√
变式训练4 如图所示,在同一竖直线上有A、B两点,相距为h,B点离地高度为H,现在要在地面上寻找一点P,使得从A、B两点分别向点P安放的光滑木板,满足物体从静止开始分别由A和B沿木板 下滑到P点的时间相等,求O、P两点之间的距离 。
【解析】由“等时圆”特征可知,当A、B处于等时圆周上,且P点处于等时圆的最低点 时,即能满足题设要求。如图所示,此时等时圆的半径为:
A
B
P
H
h
O
变式训练5 倾角为30°的长斜坡上有C、O、B三点,CO = OB = 10m,在C点竖直地固定一长10 m的直杆AO。A端与C点间和坡底B点间各连有一光滑的钢绳,且各穿有一钢球(视为质点),将两球从A点由静止开始、同时分别沿两钢绳滑到钢绳末端,如图 1所示,则小球在钢绳上tAC 和tAB分别为 (取g = 10m/s2)
A.2s和2s B. 和 2s
C. 和4s D.4s 和
解析 作三角形 外接圆,由弦轨道等时性得出
= =2s
A
O
B
C
30°
α1
α2
D
tAC=tAB
√
变式训练6 如图,圆柱体的仓库内有三块长度不同的滑板aO、bO、cO,其下 端都固定于底部圆心O,而上端则搁在仓库侧壁,三块滑块与水平面的夹角依次为300、450、600。若有三个小孩同时从a、b、c处开始下滑(忽略阻力),则 ( )
A、a处小孩最先到O点 B、b处小孩最后到O点
C、c处小孩最先到O点 D、a、c处小孩同时到O点
解析 把abc等效在一个竖直平面上,b 处小孩最先到O点
在作出三角形aco外接圆,o点恰好在最低点,
a、c处小孩同时到O点。
θ
a
O
b
c
√
2021年高考物理三轮复习解题方法专题
方法概述
01
物理问题通常都配有一个与真实的物理情境相对应的示意图形,在对研究对象进行受力分析、描画轨迹、分解速度、描绘光路时,会形成各种各样的几何形状,分析求解时经常要用到几何方法——相似三角形法、几何作图法.
02
相似三角形法
一、相似三角形法
在共点力平衡问题、运动的合成和分解、电磁场的合成和分解以及几何光学等物理情境中,常会出现力三角形、速度三角形、位移三角形等矢量三角形和结构(长度)三角形相似的情况,准确作图、仔细观察、灵活选用相似三角形的边角关系是解题的关键.
相似三角形的一些性质:①对应角相等;②对应边成比例;③对应的垂线、中线、角平分线成比例.
圆的几何知识及应用
例1.如图所示,三个固定的带电小球a、b和c,相互间的距离分别为ab=5 cm,bc=3 cm,ca=4 cm.小球c所受库仑力的合力的方向平行于a、b的连线.设小球a、b所带电荷量的比值的绝对值为k,则 ( )
A.a、b的电荷同号,k= B.a、b的电荷异号,k=
C.a、b的电荷同号,k= D.a、b的电荷异号,k=
?
?
【解析】]当c所受a、b的库仑力的合力与a、b连线平行时,场强如图甲或乙所示.所以,a、b的电荷一定异号,Ea= 、Eb= ,由图可知 = ,解得 = ,D正确.
√
变式训练1 如图所示,两球A、B用劲度系数为k1的轻弹簧相连,球B用长为L的细绳悬于O点,球A固定在O点正下方,且点O、A之间的距离恰为L,系统平衡时绳子所受的拉力为F1.现把A、B间的弹簧换成劲度系数为k2的轻弹(k2>k1),仍使系统平衡,此时绳子所受拉力为F2,则F1与F2的大小关系为( )
A.F1>F2 B.F1=F2
C.F1
【解析】 以小球B为研究对象分析受力情况,小球B受到重力、细绳拉力F和弹簧弹力FN的作用处于平衡状态,由共点力的平衡条件可知,弹簧的弹力FN和绳子的拉力F的合力F合与重力mg大小相等,方向相反,作出小球B的受力图,由于三角形OAB与三角形BCD相似,故有 = ,由于OA=OB=L,F合=mg,故绳子的拉力F与弹簧的弹力无关即与弹簧劲度系数无关,只与小球所受重力有关,即有F1=F2,故B正确,A、C、D错误.
例2 一条宽为L的河流,水流速度为 u,船在静水中划行的速度为v ,且 。要使船到达对岸的位移最短,船的航向如何?最短位移多大?
解析:水流速度 u、船在静水中的速度v 与船的合速度 构成一矢量三角形,且船在静水中的速度 大小不变,方向不定,构建如图1所示的矢量圆。显然,当AD与矢量圆相切时,船航行的位移最短。由图可得船的航向与河岸的夹角 由相似三角形得
最短位移
二、几何作图法
我们先看弦轨道模型问题并证明物体下滑的等时性。
如图所示,让物体从竖直圆环上的最高点A处由静止开始沿光滑的弦轨道AB 、AC、AD下滑(AD竖直),下滑的时间分别为 、 、 。试证明
证明:物体由静止开始沿AB弦轨道下滑,AB弦轨道长为 ,AB弦轨道与竖直方向夹角为 ,直径AD长为 。
①
②
③
①②③解得:
可知物体由静止开始沿光滑弦轨道下滑的时间与弦与竖直方向的夹角无关,即
(1)质点在竖直圆环上沿不同的光滑弦从其上端由静止开始滑到环的最低点所用时间相等,如图甲所示。
(2)质点从竖直圆环上最高点沿不同的光滑弦由静止开始滑到下端所用时间相等,如图乙所示。
依据弦轨道等时性特点,可以用作图的方法解题
例3 在倾角为θ的斜面上方的A点放置一光滑的木板AB,B端刚好在斜面上,木板与竖直方向所成角度为α,一小物块由A端沿木板由静止下滑,要使物块滑到斜面的时间最短,则α与θ角的大小关系为( )。
A.α=θ B.α= C.α=2θ D.α=
【解析】作法:过A点作竖直线AB,过A作水平线与斜面交Q点,作 的角平分线与AB交于O点,以O点为圆心、AO长为半径作圆切斜面于P点,AP径迹即为最短时间。∠POB=θ,则α= ,B项正确。
√
变式训练2 如图所示,在竖直平面内建立直角坐标系xOy,该平面内有AM、BM、CM三条光滑固定轨道,其中AM=MC
D.无法比较时间大小关系
解析 作三角形MBC外接圆,由弦轨道等时性特点得出 tA=tC
变式训练3 为了使雨滴能尽快地淌离房顶,要设计好房顶的高度(围墙已建好),设雨滴沿房顶下淌时做无初速度无摩擦的运动,那么如图所示的四种情况符合要求的是( C )
解析 以横梁的中点M为圆心,以横梁长度的二分之一为半径画圆,由弦轨道的等时性可以得出45度角的房顶,雨滴下滑时间最短。
?
?
?
√
变式训练4 如图所示,在同一竖直线上有A、B两点,相距为h,B点离地高度为H,现在要在地面上寻找一点P,使得从A、B两点分别向点P安放的光滑木板,满足物体从静止开始分别由A和B沿木板 下滑到P点的时间相等,求O、P两点之间的距离 。
【解析】由“等时圆”特征可知,当A、B处于等时圆周上,且P点处于等时圆的最低点 时,即能满足题设要求。如图所示,此时等时圆的半径为:
A
B
P
H
h
O
变式训练5 倾角为30°的长斜坡上有C、O、B三点,CO = OB = 10m,在C点竖直地固定一长10 m的直杆AO。A端与C点间和坡底B点间各连有一光滑的钢绳,且各穿有一钢球(视为质点),将两球从A点由静止开始、同时分别沿两钢绳滑到钢绳末端,如图 1所示,则小球在钢绳上tAC 和tAB分别为 (取g = 10m/s2)
A.2s和2s B. 和 2s
C. 和4s D.4s 和
解析 作三角形 外接圆,由弦轨道等时性得出
= =2s
A
O
B
C
30°
α1
α2
D
tAC=tAB
√
变式训练6 如图,圆柱体的仓库内有三块长度不同的滑板aO、bO、cO,其下 端都固定于底部圆心O,而上端则搁在仓库侧壁,三块滑块与水平面的夹角依次为300、450、600。若有三个小孩同时从a、b、c处开始下滑(忽略阻力),则 ( )
A、a处小孩最先到O点 B、b处小孩最后到O点
C、c处小孩最先到O点 D、a、c处小孩同时到O点
解析 把abc等效在一个竖直平面上,b 处小孩最先到O点
在作出三角形aco外接圆,o点恰好在最低点,
a、c处小孩同时到O点。
θ
a
O
b
c
√
同课章节目录
