青岛版 八年级下册 6.1平行四边形及其性质同步课时训练(word版含答案)
文档属性
| 名称 | 青岛版 八年级下册 6.1平行四边形及其性质同步课时训练(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 478.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 00:00:00 | ||
图片预览




文档简介
6.1平行四边形及其性质同步课时训练
一、单选题
1.如图,在中,,对角线与相交于点,交于,若的周长为,则的周长是( )
A. B. C. D.无法确定
2.如图,四边形是平行四边形,P是上一点,且和分别平分和.如果,,则的面积等于( ).
A.24 B.30 C. D.
3.在面积为15的平行四边形中,过点A作垂直于直线于点E,作垂直于直线于点F,若,,则的值为( )
A. B.
C.或 D.或
4.如图所示,在平行四边形ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( )
A.2 cm B.3 cm C.4 cm D.5 cm
5.如图,已知的面积为点在线段上,点在线段的延长线上,且四边形是平行四边形,则图中阴影部分的面积为( )
A.
B.
C.
D.
6.如图,的对角线交于点平分交于点,连接.下列结论:①;②平分;③;④垂直平分.其中正确的个数有( )
A.个
B.个
C.个
D.个
7.如图,在平行四边形中,平分,,,则平行四边形的周长是( )
A.16 B.14 C.20 D.24
8.如图,在平行四边形中,,则等于( )
A.50° B.65° C.100° D.130°
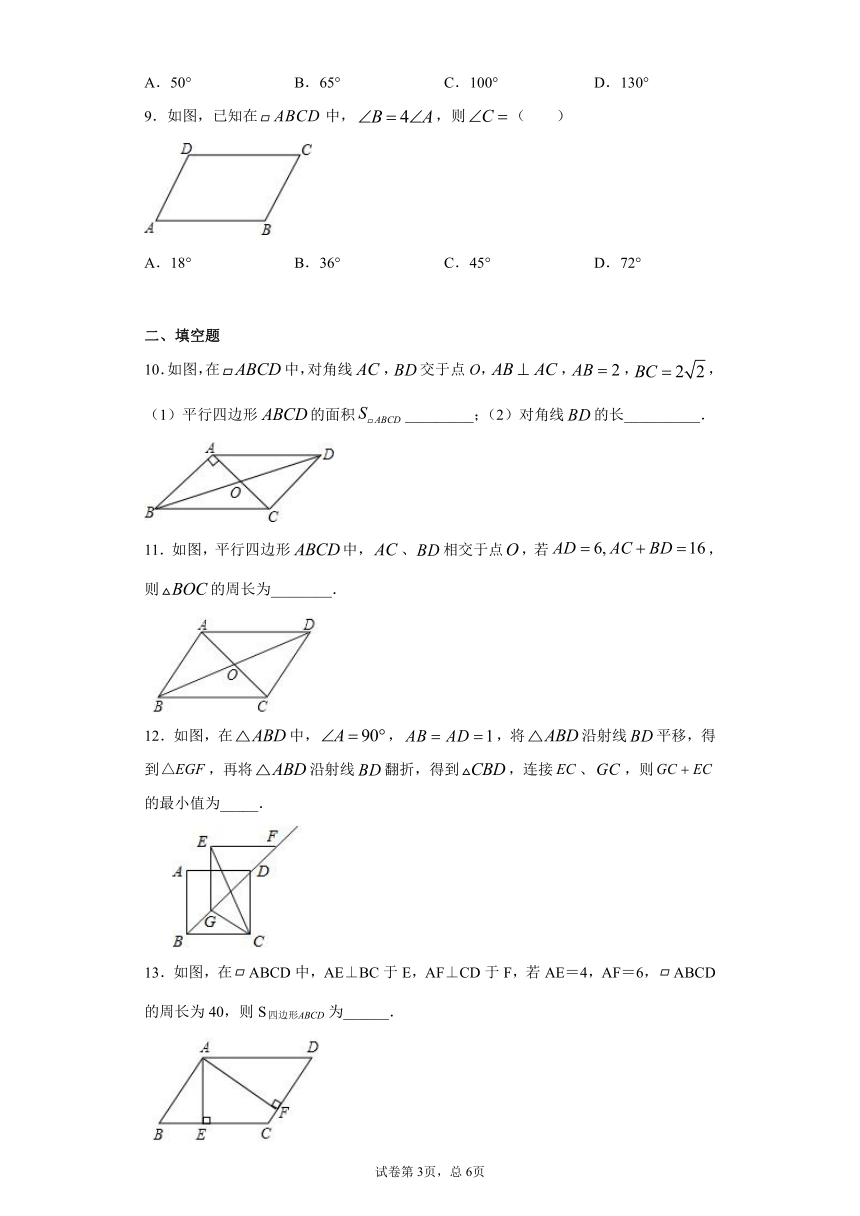
9.如图,已知在中,,则( )
A.18° B.36° C.45° D.72°
二、填空题
10.如图,在中,对角线,交于点O,,,,(1)平行四边形的面积_________;(2)对角线的长__________.
11.如图,平行四边形中,、相交于点,若,则的周长为________.
12.如图,在中,,,将沿射线平移,得到,再将沿射线翻折,得到,连接、,则的最小值为_____.
13.如图,在ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,ABCD的周长为40,则S为______.
14.如图,在平行四边形中,的平分线与的延长线交于点E?与交于点F,且点F为边的中点,的平分线交于点M,交于点N,连接.若,则的长为_______.
15.如图所示,在平行四边形中,平分交边于点,且,则的长为______.
16.如图,将沿对角线进行折叠,折叠后点D落在点F处,交于点E,有下列结论:①;②;③;④,其中正确结论的是__________.
三、解答题
17.如图,在四边形中,.动点P从点B出发,沿射线的方向以每秒的速度运动到C点返回,动点Q从点A出发,在线段上以每秒的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动时间为t(秒).
(1)当时,若四边形是平行四边形,求出满足要求的t的值;
(2)当时,若以C,D,Q,P为顶点的四边形面积为,求相应的t的值;
(3)当时,若以C,D,Q,P为顶点的四边形面积为,求相应的t的值.
18.如图,在□ ABCD中,点P在对角线AC上一动点,过点P作PM//DC,且PM=DC,连接BM,CM,AP,BD.
(1)求证: △ADP≌△BCM;
(2)若PA=PC,设△ABP的面积为S,四边形BPCM的面积为T,求的值.
19.在中,,点E在边所在的直线上,过点E作交直线于点D,交直线于点F,构造出平行四边形.
(1)若点E在线段上时.
①求证:.
②求证:.
(2)点E在边所在的直线上,若,,请作出简单示意图并直接写出的长度.
20.如图,点在内部,.
(1)求证:;
(2)求证:
参考答案
1.A
2.A
3.D
4.A
5.A
6.C
7.C
8.A
9.B
10.4
11.14
12.
13.48
14.
15.4
16.①②③
17.(1)t=5;(2)t=9;(3)t=15
【详解】
解:(1)∵四边形PQDC是平行四边形,
∴DQ=CP,
当0<t<10.5时,P、Q分别沿AD、BC运动,如图1所示:
∵DQ=AD-AQ=16-t,
CP=21-2t
∴16-t=21-2t
解得:t=5;
即当t=5秒时,四边形PQDC是平行四边形;
(2)当0<t<10.5时,P、Q分别沿AD、BC运动,如图1所示:
CP=21-2t,DQ=16-t,
若以C,D,Q,P为顶点的四边形面积为60cm2,
则(DQ+CP)×AB=60,
即(16-t+21-2t)×12=60,
解得:t=9;
即当0<t<10.5时,若以C,D,Q,P为顶点的四边形面积为60cm2,t的值为9秒;
(3)当10.5≤t<16时,如图2所示,点P到达C点返回,CP=2t-21,DQ=16-t,
则同(2)得:(DQ+CP)×AB=60,
即(16-t+2t-21)×12=60,
解得:t=15.
即当10.5≤t<16时,若以C,D,Q,P为顶点的四边形面积为60cm2,t的值为15秒.
18.(1)证明见解析;(2)
【详解】
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ADC+∠BCD=,
∵PM//DC,且PM=DC,
∴四边形PMCD是平行四边形,
∴PD=CM,∠PDC+∠DCM=,
∴∠ADP=∠BCM,
∴△ADP≌△BCM;
(2)解:作BH⊥AC于H,DG⊥AC于G,
∵四边形ABCD是平行四边形,
∴△ABC≌△CDA,
∴BH=DG,
∴,即,
,即,
∵△ADP≌△BCM,
∴,
∴=.
19.(1)①见解析;②见解析;(2)10或6
【详解】
解:(1)①∵EF∥AC,
∴∠FEB=∠A,
又∵AC=BC,
∴∠B=∠A,
∴∠FEB=∠B,
∴FE=FB;
②∵EF∥AC,DE∥BC,
∴四边形CDEF是平行四边形.
∴CF=DE,
∵EF=BF,
∴DE+EF=CF+BF=BC;
(2)如图,同理可得:BF=EF,
∴DE=BC+BF=BC+EF=8+2=10.
如图,同理可得:BF=EF,
DE=CF=BF-BC=EF-BC=2-8=-6(不合题意).
如图④,
DE=BC-BF=BC-EF=8-2=6.
20.(1)见解析;(2)见解析
【详解】
解:四边形是平行四边形,
,
同理得
点在内部,
∴,
由知:
∴.
一、单选题
1.如图,在中,,对角线与相交于点,交于,若的周长为,则的周长是( )
A. B. C. D.无法确定
2.如图,四边形是平行四边形,P是上一点,且和分别平分和.如果,,则的面积等于( ).
A.24 B.30 C. D.
3.在面积为15的平行四边形中,过点A作垂直于直线于点E,作垂直于直线于点F,若,,则的值为( )
A. B.
C.或 D.或
4.如图所示,在平行四边形ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( )
A.2 cm B.3 cm C.4 cm D.5 cm
5.如图,已知的面积为点在线段上,点在线段的延长线上,且四边形是平行四边形,则图中阴影部分的面积为( )
A.
B.
C.
D.
6.如图,的对角线交于点平分交于点,连接.下列结论:①;②平分;③;④垂直平分.其中正确的个数有( )
A.个
B.个
C.个
D.个
7.如图,在平行四边形中,平分,,,则平行四边形的周长是( )
A.16 B.14 C.20 D.24
8.如图,在平行四边形中,,则等于( )
A.50° B.65° C.100° D.130°
9.如图,已知在中,,则( )
A.18° B.36° C.45° D.72°
二、填空题
10.如图,在中,对角线,交于点O,,,,(1)平行四边形的面积_________;(2)对角线的长__________.
11.如图,平行四边形中,、相交于点,若,则的周长为________.
12.如图,在中,,,将沿射线平移,得到,再将沿射线翻折,得到,连接、,则的最小值为_____.
13.如图,在ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,ABCD的周长为40,则S为______.
14.如图,在平行四边形中,的平分线与的延长线交于点E?与交于点F,且点F为边的中点,的平分线交于点M,交于点N,连接.若,则的长为_______.
15.如图所示,在平行四边形中,平分交边于点,且,则的长为______.
16.如图,将沿对角线进行折叠,折叠后点D落在点F处,交于点E,有下列结论:①;②;③;④,其中正确结论的是__________.
三、解答题
17.如图,在四边形中,.动点P从点B出发,沿射线的方向以每秒的速度运动到C点返回,动点Q从点A出发,在线段上以每秒的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动时间为t(秒).
(1)当时,若四边形是平行四边形,求出满足要求的t的值;
(2)当时,若以C,D,Q,P为顶点的四边形面积为,求相应的t的值;
(3)当时,若以C,D,Q,P为顶点的四边形面积为,求相应的t的值.
18.如图,在□ ABCD中,点P在对角线AC上一动点,过点P作PM//DC,且PM=DC,连接BM,CM,AP,BD.
(1)求证: △ADP≌△BCM;
(2)若PA=PC,设△ABP的面积为S,四边形BPCM的面积为T,求的值.
19.在中,,点E在边所在的直线上,过点E作交直线于点D,交直线于点F,构造出平行四边形.
(1)若点E在线段上时.
①求证:.
②求证:.
(2)点E在边所在的直线上,若,,请作出简单示意图并直接写出的长度.
20.如图,点在内部,.
(1)求证:;
(2)求证:
参考答案
1.A
2.A
3.D
4.A
5.A
6.C
7.C
8.A
9.B
10.4
11.14
12.
13.48
14.
15.4
16.①②③
17.(1)t=5;(2)t=9;(3)t=15
【详解】
解:(1)∵四边形PQDC是平行四边形,
∴DQ=CP,
当0<t<10.5时,P、Q分别沿AD、BC运动,如图1所示:
∵DQ=AD-AQ=16-t,
CP=21-2t
∴16-t=21-2t
解得:t=5;
即当t=5秒时,四边形PQDC是平行四边形;
(2)当0<t<10.5时,P、Q分别沿AD、BC运动,如图1所示:
CP=21-2t,DQ=16-t,
若以C,D,Q,P为顶点的四边形面积为60cm2,
则(DQ+CP)×AB=60,
即(16-t+21-2t)×12=60,
解得:t=9;
即当0<t<10.5时,若以C,D,Q,P为顶点的四边形面积为60cm2,t的值为9秒;
(3)当10.5≤t<16时,如图2所示,点P到达C点返回,CP=2t-21,DQ=16-t,
则同(2)得:(DQ+CP)×AB=60,
即(16-t+2t-21)×12=60,
解得:t=15.
即当10.5≤t<16时,若以C,D,Q,P为顶点的四边形面积为60cm2,t的值为15秒.
18.(1)证明见解析;(2)
【详解】
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ADC+∠BCD=,
∵PM//DC,且PM=DC,
∴四边形PMCD是平行四边形,
∴PD=CM,∠PDC+∠DCM=,
∴∠ADP=∠BCM,
∴△ADP≌△BCM;
(2)解:作BH⊥AC于H,DG⊥AC于G,
∵四边形ABCD是平行四边形,
∴△ABC≌△CDA,
∴BH=DG,
∴,即,
,即,
∵△ADP≌△BCM,
∴,
∴=.
19.(1)①见解析;②见解析;(2)10或6
【详解】
解:(1)①∵EF∥AC,
∴∠FEB=∠A,
又∵AC=BC,
∴∠B=∠A,
∴∠FEB=∠B,
∴FE=FB;
②∵EF∥AC,DE∥BC,
∴四边形CDEF是平行四边形.
∴CF=DE,
∵EF=BF,
∴DE+EF=CF+BF=BC;
(2)如图,同理可得:BF=EF,
∴DE=BC+BF=BC+EF=8+2=10.
如图,同理可得:BF=EF,
DE=CF=BF-BC=EF-BC=2-8=-6(不合题意).
如图④,
DE=BC-BF=BC-EF=8-2=6.
20.(1)见解析;(2)见解析
【详解】
解:四边形是平行四边形,
,
同理得
点在内部,
∴,
由知:
∴.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
