青岛版 八年级下6.3特殊的平行四边形同步课时训练(word版含答案)
文档属性
| 名称 | 青岛版 八年级下6.3特殊的平行四边形同步课时训练(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 417.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 00:00:00 | ||
图片预览

文档简介
6.3特殊的平行四边形同步课时训练
一、单选题
1.如图,矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD于点F,交AC于点M,过点D作DE∥BF交AB于点E,交AC于点N,连接FN,EM.则下列结论:①DN=BM;②EM//FN;③AE=FC;④当AO=AD时,四边形DEBF是菱形.其中,正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
2.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66° B.60° C.57° D.48°
3.如图,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上,∠EFD=60°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则BE的长度为( )
A.1 B. C. D.2
4.如图,矩形ABCD中,AB=6cm,AD=4cm,点M是边AB的中点,点P是矩形边上的一个动点,点P从M出发在矩形的边上沿着逆时针方向运动,则当点P沿着矩形的边逆时针旋转一周时,△DMP面积刚好为5cm2的时刻有(?? )
A.2个 B.3个 C.4个 D.5个
5.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE B.DE⊥DC C.∠ADB=90° D.CE⊥DE
6.下列性质中,菱形具有而矩形不一定具有的是( )
A.对角线相等 B.对角线垂直 C.邻边垂直 D.邻角互补
7.如图,在四边形中,对角线,相交于点,且,.若要使四边形为矩形,则可以添加的条件是( )
A. B. C. D.
8.如图,在长方形ABCD中,AE平分∠BAD交BC于点E,连接ED,若ED=5,EC=3,则长方形的周长为( )
A.20 B.22 C.24 D.26
9.如图,边长为的正方形,剪去四个角后成为一个正八边形,则这个正八边形的边长为( )
A.0.5 B. C.1 D.
10.如图所示,在菱形中,,,则菱形的周长是( ).
A.20 B.15 C.10 D.5
二、填空题
11.在矩形ABCD中,AB=5,BC=7,点P是直线BC一动点,若将△ABP沿AP折叠,使点B落在平面上的点E处,连结AE、PE.若P、E、D三点在一直线上,则BP=_________.
12.如图,已知为线段上的一点,分别以为边在的同侧作菱形和菱形.点在一条直线上,,分别是对角线,的中点.当时,则:
(1)____________________.
(2)点之间的距离为____________________.(结果留根号).
13.如图,在菱形ABCD中,AB=4,∠ABC=60°,点M、N分别是BC、CD上任意一点,点P是BD上一点,连接PM、PN,则PM+PN的最小值为________.
14.如图,在矩形中,平分交于点E,交于点F,若,,则等于________.
15.如图,四边形ABCD是一个正方形,E是BC延长线上一点,且AC=EC,则∠DAE的度数为_________.
16.如图,在四边形ABCD中,DA=DC,∠ABC=∠ADC=90°,S四边形ABCD=12cm2,则BE=_____cm.
三、解答题
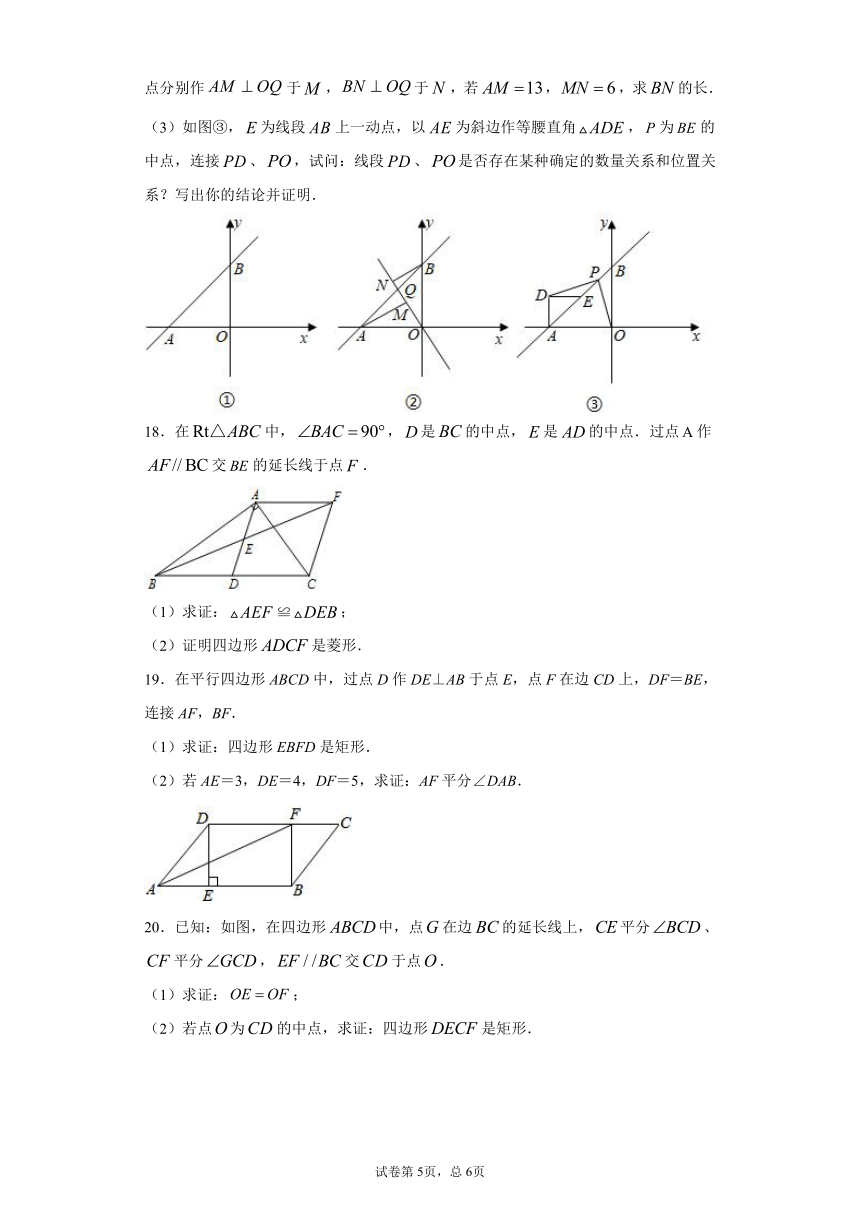
17.如图①,直线与轴负半轴、轴正半轴分别交于、两点.、的长度分别为和,且满足.
(1)判断的形状.
(2)如图②,正比例函数()的图像与直线交于点,过、两点分别作于,于,若,,求的长.
(3)如图③,为线段上一动点,以为斜边作等腰直角,为的中点,连接、,试问:线段、是否存在某种确定的数量关系和位置关系?写出你的结论并证明.
18.在中,,是的中点,是的中点.过点作交的延长线于点.
(1)求证:≌;
(2)证明四边形是菱形.
19.在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形EBFD是矩形.
(2)若AE=3,DE=4,DF=5,求证:AF平分∠DAB.
20.已知:如图,在四边形中,点在边的延长线上,平分、平分,交于点.
(1)求证:;
(2)若点为的中点,求证:四边形是矩形.
参考答案
1.D
2.C
3.D
4.C
5.B
6.B
7.B
8.B
9.D
10.A
11.7+2或7﹣2
12.
13.6
14.7
15.22.5°
16.
17.(1)等腰直角三角形;(2);(3)且,证明见解析
【详解】
解:(1)是等腰直角三角形.
理由:
∵,
∴,
∴,
∴,即.
∵,
∴为等腰直角三角形.
(2)∵,,
∴,
∵,,
∴,
在和中,
,
∴≌,
∴,,
∵,,
∴,
∴,
∴.
(3)且,
如图,延长到点,使,连接、、,
在和,
.
∴≌,
∴,,
则,
又∵,,
∴,
在和,
,
∴≌,
∴,,
∴,
∴为等腰直角三角形,
∵,
∴,.
18.(1)见解析;(2)见解析.
【详解】
(1)∵,
∴,
∵是中点,是边上的中线,
∴,,
在和中,
,
∴≌(AAS).
(2)由(1)知≌,
则,
∵,
∴,
∵,
∴四边形是平行四边形,
∵,是的中点,是中点,
∴,
∴四边形是菱形.
19.(1)见解析;(2)见解析.
【详解】
证明:(1)∵四边形ABCD为平行四边形,
∴DC∥AB,即DF∥BE,
又∵DF=BE,
∴四边形DEBF为平行四边形,
又∵DE⊥AB,
∴∠DEB=90°,
∴四边形DEBF为矩形;
(2)∵∠DEB=90°,
∴∠DEA=90°,
∵AE=3,DE=4,
∴AD= ,
∵DF=5,
∴AD=DF,
∴∠DAF=∠DFA,
∵AB∥CD,
∴∠FAB=∠DFA,
∴∠FAB=∠FAD,
∴AF平分∠DAB.
20.(1)见解析;(2)见解析
【详解】
证明:(1)∵平分、平分
∴,
∵∥,
∴,
∴,
∴,,
∴.
(2)∵点为的中点,
∴,又,
∴四边形是平行四边形
∵平分、平分,
∴,
∴
∵,
∴
∵四边形是平行四边形,
∴平行四边形是矩形.
一、单选题
1.如图,矩形ABCD中,AC,BD相交于点O,过点B作BF⊥AC交CD于点F,交AC于点M,过点D作DE∥BF交AB于点E,交AC于点N,连接FN,EM.则下列结论:①DN=BM;②EM//FN;③AE=FC;④当AO=AD时,四边形DEBF是菱形.其中,正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
2.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于( )
A.66° B.60° C.57° D.48°
3.如图,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上,∠EFD=60°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则BE的长度为( )
A.1 B. C. D.2
4.如图,矩形ABCD中,AB=6cm,AD=4cm,点M是边AB的中点,点P是矩形边上的一个动点,点P从M出发在矩形的边上沿着逆时针方向运动,则当点P沿着矩形的边逆时针旋转一周时,△DMP面积刚好为5cm2的时刻有(?? )
A.2个 B.3个 C.4个 D.5个
5.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE B.DE⊥DC C.∠ADB=90° D.CE⊥DE
6.下列性质中,菱形具有而矩形不一定具有的是( )
A.对角线相等 B.对角线垂直 C.邻边垂直 D.邻角互补
7.如图,在四边形中,对角线,相交于点,且,.若要使四边形为矩形,则可以添加的条件是( )
A. B. C. D.
8.如图,在长方形ABCD中,AE平分∠BAD交BC于点E,连接ED,若ED=5,EC=3,则长方形的周长为( )
A.20 B.22 C.24 D.26
9.如图,边长为的正方形,剪去四个角后成为一个正八边形,则这个正八边形的边长为( )
A.0.5 B. C.1 D.
10.如图所示,在菱形中,,,则菱形的周长是( ).
A.20 B.15 C.10 D.5
二、填空题
11.在矩形ABCD中,AB=5,BC=7,点P是直线BC一动点,若将△ABP沿AP折叠,使点B落在平面上的点E处,连结AE、PE.若P、E、D三点在一直线上,则BP=_________.
12.如图,已知为线段上的一点,分别以为边在的同侧作菱形和菱形.点在一条直线上,,分别是对角线,的中点.当时,则:
(1)____________________.
(2)点之间的距离为____________________.(结果留根号).
13.如图,在菱形ABCD中,AB=4,∠ABC=60°,点M、N分别是BC、CD上任意一点,点P是BD上一点,连接PM、PN,则PM+PN的最小值为________.
14.如图,在矩形中,平分交于点E,交于点F,若,,则等于________.
15.如图,四边形ABCD是一个正方形,E是BC延长线上一点,且AC=EC,则∠DAE的度数为_________.
16.如图,在四边形ABCD中,DA=DC,∠ABC=∠ADC=90°,S四边形ABCD=12cm2,则BE=_____cm.
三、解答题
17.如图①,直线与轴负半轴、轴正半轴分别交于、两点.、的长度分别为和,且满足.
(1)判断的形状.
(2)如图②,正比例函数()的图像与直线交于点,过、两点分别作于,于,若,,求的长.
(3)如图③,为线段上一动点,以为斜边作等腰直角,为的中点,连接、,试问:线段、是否存在某种确定的数量关系和位置关系?写出你的结论并证明.
18.在中,,是的中点,是的中点.过点作交的延长线于点.
(1)求证:≌;
(2)证明四边形是菱形.
19.在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形EBFD是矩形.
(2)若AE=3,DE=4,DF=5,求证:AF平分∠DAB.
20.已知:如图,在四边形中,点在边的延长线上,平分、平分,交于点.
(1)求证:;
(2)若点为的中点,求证:四边形是矩形.
参考答案
1.D
2.C
3.D
4.C
5.B
6.B
7.B
8.B
9.D
10.A
11.7+2或7﹣2
12.
13.6
14.7
15.22.5°
16.
17.(1)等腰直角三角形;(2);(3)且,证明见解析
【详解】
解:(1)是等腰直角三角形.
理由:
∵,
∴,
∴,
∴,即.
∵,
∴为等腰直角三角形.
(2)∵,,
∴,
∵,,
∴,
在和中,
,
∴≌,
∴,,
∵,,
∴,
∴,
∴.
(3)且,
如图,延长到点,使,连接、、,
在和,
.
∴≌,
∴,,
则,
又∵,,
∴,
在和,
,
∴≌,
∴,,
∴,
∴为等腰直角三角形,
∵,
∴,.
18.(1)见解析;(2)见解析.
【详解】
(1)∵,
∴,
∵是中点,是边上的中线,
∴,,
在和中,
,
∴≌(AAS).
(2)由(1)知≌,
则,
∵,
∴,
∵,
∴四边形是平行四边形,
∵,是的中点,是中点,
∴,
∴四边形是菱形.
19.(1)见解析;(2)见解析.
【详解】
证明:(1)∵四边形ABCD为平行四边形,
∴DC∥AB,即DF∥BE,
又∵DF=BE,
∴四边形DEBF为平行四边形,
又∵DE⊥AB,
∴∠DEB=90°,
∴四边形DEBF为矩形;
(2)∵∠DEB=90°,
∴∠DEA=90°,
∵AE=3,DE=4,
∴AD= ,
∵DF=5,
∴AD=DF,
∴∠DAF=∠DFA,
∵AB∥CD,
∴∠FAB=∠DFA,
∴∠FAB=∠FAD,
∴AF平分∠DAB.
20.(1)见解析;(2)见解析
【详解】
证明:(1)∵平分、平分
∴,
∵∥,
∴,
∴,
∴,,
∴.
(2)∵点为的中点,
∴,又,
∴四边形是平行四边形
∵平分、平分,
∴,
∴
∵,
∴
∵四边形是平行四边形,
∴平行四边形是矩形.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
