青岛版 九年级下7.4圆锥的侧面展开图同步课时训练(word版含答案)
文档属性
| 名称 | 青岛版 九年级下7.4圆锥的侧面展开图同步课时训练(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 288.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 20:21:52 | ||
图片预览



文档简介
7.4圆锥的侧面展开图同步课时训练
一、单选题
1.以下四个命题:
①如果三角形的三个内角的度数比是3:4:5,那么这个三角形是直角三角形;
②在实数-7.5,,4,,-π,()2中,有4个有理数,2个无理数;
③有一个圆锥,与底面圆直径是且体积为的圆柱等高,如果这个圆锥的侧面展开图是半圆,那么它的母线长为;
④二次函数,自变量的两个值x1,x2对应的函数值分别为y1,y2,若|x1-1|>|x2-1|,则a(y1-y2)>0.
其中正确的命题的个数为( )
A.1个 B.2个 C.3个 D.4个
2.已知圆锥的底面半径为,高为,则这个圆锥的侧面积为( )
A. B. C. D.
3.用一个圆心角为60°半径为6的扇形作一个圆锥的侧面,则这个圆锥的底面半径为( )
A.1 B.2 C.3 D.4
4.若一个圆锥的底面半径为,高为,则圆锥的侧面展开图中圆心角的度数为( )
A. B. C. D.
5.圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为2的正三角形,则此圆锥侧面展开图扇形的弧长是( )
A.2 B. C. D.
6.如图,从一块半径是米的圆形铁皮(⊙)上剪出一个圆心角为60°的扇形(点在⊙上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )米.
A. B.
C. D.
7.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径,扇形的圆心角,则该圆锥的母线长为( ).
A. B. C. D.
8.如图所示,在矩形纸片上剪下一个扇形和一个圆形,使之恰好能围成一个圆锥模型.若扇形的半径为,圆的半径为,则与满足的数量关系是( )
A. B. C. D.
9.如图,是圆锥的母线,为底面直径,已知,圆锥的侧面积为,则的值为( )
A. B. C. D.
10.如图,点C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O恰好落在弧AB上的点D处,且(表示的长),若将此扇形OAB围成一个圆锥,则圆锥的底面半径与母线长的比为( )
A.1:3 B.1:π C.1:4 D.2:9
二、填空题
11.用一个半径为半圆纸片围成一个圆锥的侧面(接缝忽略不计),则该圆锥的高为_____. (精确到).
12.已知圆锥的底面圆半径为3cm,高为4cm,则母线长为_____cm,圆锥的侧面积为_____cm2.
13.圆锥的表面展开图由一个扇形和一个圆组成,已知扇形的半径为9,圆心角为120°,则圆锥的底面圆的半径为__________.
14.如图,已知圆锥的底面半径OB为1,高所在直线AO与母线AB的夹角为.圆锥的侧面积为______.
15.一个圆锥的底面半径是,其侧面展开图的圆心角是120°,则圆锥的母线长是______.
16.如图,从直径为的圆形纸片上剪出一个圆心角为的扇形.使点、、在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面半径是______.
三、解答题
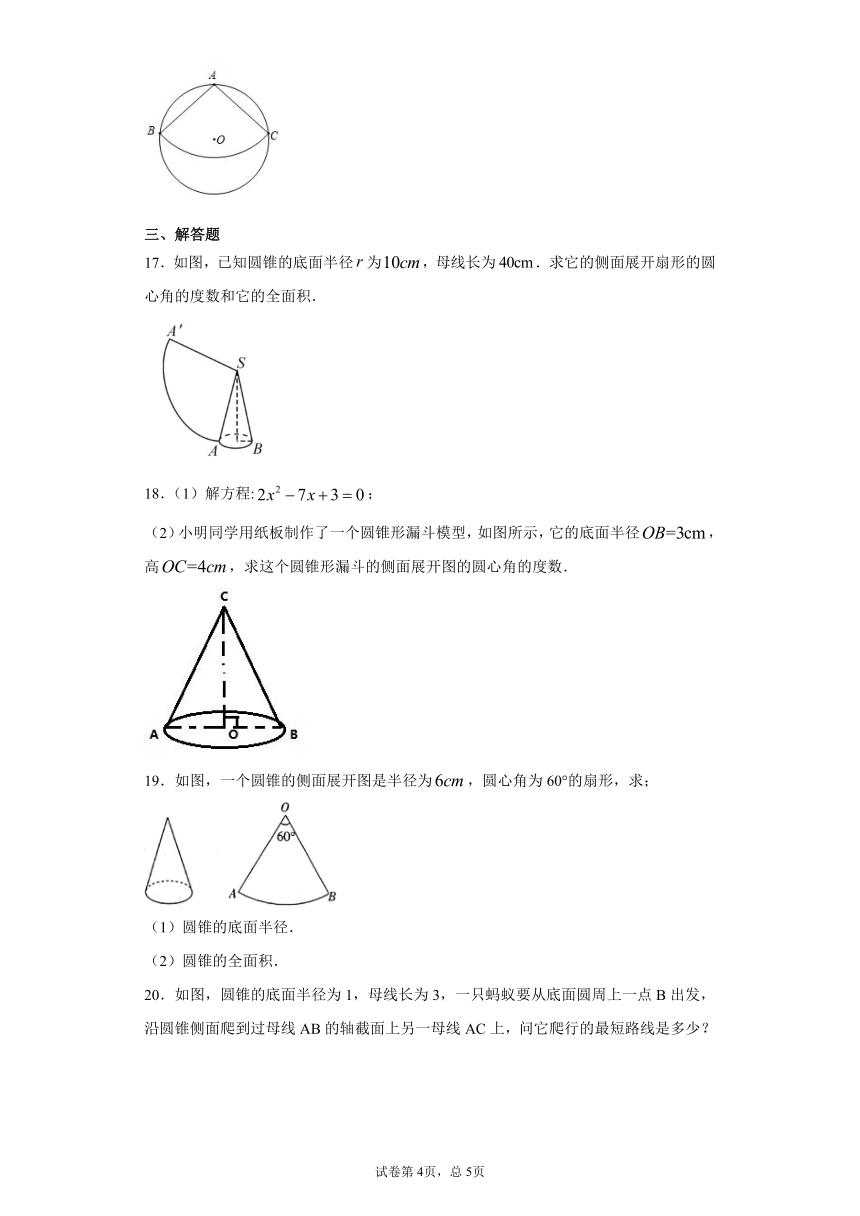
17.如图,已知圆锥的底面半径为,母线长为.求它的侧面展开扇形的圆心角的度数和它的全面积.
18.(1)解方程:;
(2)小明同学用纸板制作了一个圆锥形漏斗模型,如图所示,它的底面半径,高,求这个圆锥形漏斗的侧面展开图的圆心角的度数.
19.如图,一个圆锥的侧面展开图是半径为,圆心角为60°的扇形,求;
(1)圆锥的底面半径.
(2)圆锥的全面积.
20.如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少?
参考答案
1.C
2.B
3.A
4.A
5.C
6.B.
7.C
8.D
9.B
10.D
11.17.3
12.5 15π
13.3
14.2π.
15.12cm
16.2
17.90°,
【详解】
解:由圆锥的底面圆的周长等于侧面展开扇形的弧长可知:
,,
∴侧面展开扇形的圆心角的度数是90°.
全面积=底面积+展开侧面积,
全面积为:.
18.(1);(2)这个圆锥形漏斗的侧面展开图的圆心角的度数为216°
【详解】
解:(1)
a=2,b=-7,c=3
∴x=
解得:;
(2)该圆锥侧面展开图的半径BC=
侧面展开图的弧长即为底面圆的周长为cm
∴侧面展开图的圆心角的度数为
答:这个圆锥形漏斗的侧面展开图的圆心角的度数为216°.
19.(1);(2)
【详解】
(1)设圆锥的底面半径为,
扇形的弧长,
∴
解得,,即圆锥的底面半径为;
(2)圆锥的全面积.
20.
【详解】
如图,沿过母线AB的轴截面展开得扇形,
此时弧的长为底面圆周长的一半,故,
由,,则,
作,此时即为蚂蚁爬行的最短路径,
在中,.
一、单选题
1.以下四个命题:
①如果三角形的三个内角的度数比是3:4:5,那么这个三角形是直角三角形;
②在实数-7.5,,4,,-π,()2中,有4个有理数,2个无理数;
③有一个圆锥,与底面圆直径是且体积为的圆柱等高,如果这个圆锥的侧面展开图是半圆,那么它的母线长为;
④二次函数,自变量的两个值x1,x2对应的函数值分别为y1,y2,若|x1-1|>|x2-1|,则a(y1-y2)>0.
其中正确的命题的个数为( )
A.1个 B.2个 C.3个 D.4个
2.已知圆锥的底面半径为,高为,则这个圆锥的侧面积为( )
A. B. C. D.
3.用一个圆心角为60°半径为6的扇形作一个圆锥的侧面,则这个圆锥的底面半径为( )
A.1 B.2 C.3 D.4
4.若一个圆锥的底面半径为,高为,则圆锥的侧面展开图中圆心角的度数为( )
A. B. C. D.
5.圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为2的正三角形,则此圆锥侧面展开图扇形的弧长是( )
A.2 B. C. D.
6.如图,从一块半径是米的圆形铁皮(⊙)上剪出一个圆心角为60°的扇形(点在⊙上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )米.
A. B.
C. D.
7.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径,扇形的圆心角,则该圆锥的母线长为( ).
A. B. C. D.
8.如图所示,在矩形纸片上剪下一个扇形和一个圆形,使之恰好能围成一个圆锥模型.若扇形的半径为,圆的半径为,则与满足的数量关系是( )
A. B. C. D.
9.如图,是圆锥的母线,为底面直径,已知,圆锥的侧面积为,则的值为( )
A. B. C. D.
10.如图,点C为扇形OAB的半径OB上一点,将△OAC沿AC折叠,点O恰好落在弧AB上的点D处,且(表示的长),若将此扇形OAB围成一个圆锥,则圆锥的底面半径与母线长的比为( )
A.1:3 B.1:π C.1:4 D.2:9
二、填空题
11.用一个半径为半圆纸片围成一个圆锥的侧面(接缝忽略不计),则该圆锥的高为_____. (精确到).
12.已知圆锥的底面圆半径为3cm,高为4cm,则母线长为_____cm,圆锥的侧面积为_____cm2.
13.圆锥的表面展开图由一个扇形和一个圆组成,已知扇形的半径为9,圆心角为120°,则圆锥的底面圆的半径为__________.
14.如图,已知圆锥的底面半径OB为1,高所在直线AO与母线AB的夹角为.圆锥的侧面积为______.
15.一个圆锥的底面半径是,其侧面展开图的圆心角是120°,则圆锥的母线长是______.
16.如图,从直径为的圆形纸片上剪出一个圆心角为的扇形.使点、、在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面半径是______.
三、解答题
17.如图,已知圆锥的底面半径为,母线长为.求它的侧面展开扇形的圆心角的度数和它的全面积.
18.(1)解方程:;
(2)小明同学用纸板制作了一个圆锥形漏斗模型,如图所示,它的底面半径,高,求这个圆锥形漏斗的侧面展开图的圆心角的度数.
19.如图,一个圆锥的侧面展开图是半径为,圆心角为60°的扇形,求;
(1)圆锥的底面半径.
(2)圆锥的全面积.
20.如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少?
参考答案
1.C
2.B
3.A
4.A
5.C
6.B.
7.C
8.D
9.B
10.D
11.17.3
12.5 15π
13.3
14.2π.
15.12cm
16.2
17.90°,
【详解】
解:由圆锥的底面圆的周长等于侧面展开扇形的弧长可知:
,,
∴侧面展开扇形的圆心角的度数是90°.
全面积=底面积+展开侧面积,
全面积为:.
18.(1);(2)这个圆锥形漏斗的侧面展开图的圆心角的度数为216°
【详解】
解:(1)
a=2,b=-7,c=3
∴x=
解得:;
(2)该圆锥侧面展开图的半径BC=
侧面展开图的弧长即为底面圆的周长为cm
∴侧面展开图的圆心角的度数为
答:这个圆锥形漏斗的侧面展开图的圆心角的度数为216°.
19.(1);(2)
【详解】
(1)设圆锥的底面半径为,
扇形的弧长,
∴
解得,,即圆锥的底面半径为;
(2)圆锥的全面积.
20.
【详解】
如图,沿过母线AB的轴截面展开得扇形,
此时弧的长为底面圆周长的一半,故,
由,,则,
作,此时即为蚂蚁爬行的最短路径,
在中,.
