青岛版 九年级下8.1中心投影同步课时训练(word版含答案)
文档属性
| 名称 | 青岛版 九年级下8.1中心投影同步课时训练(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 249.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 00:00:00 | ||
图片预览



文档简介
8.1中心投影同步课时训练
一、单选题
1.在小明住的小区有一条笔直的路,路中间有一盏路灯,一天晚上他行走在这条路上如图,当他从点走到点的过程,他在灯光照射下的影长与所走路程的变化关系图象大致是( )
A. B. C. D.
2.如图,在平面直角坐标系中,点是一个光源.木杆AB两端的坐标分别为,.则木杆AB在x轴上的投影长为( ).
A.4 B.5 C.6 D.8
3.一个等边三角形在太阳光的照射下,在地面上的投影不可能是( )
A. B. C. D.
4.如图,晚上小亮在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子( )
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短
5.如图,白炽灯下有一个乒乓球,当乒乓球越接近灯泡时,它在地面上的影子( )
A.越大 B.越小 C.不变 D.无法确定
6.如图,小明夜晚从路灯下A处走到B处这一过程中,他在路上的影子( )
A.逐渐变长 B.逐渐变短
C.长度不变 D.先变短后变长
7.下列哪种光线形成的投影不是中心投影( )
A.台灯 B.太阳 C.手电筒 D.路灯
8.晚上,王老师出去散步,他先走向一盏路灯,然后离路灯而去,他会发现自己的身影是( )
A.变长 B.变短 C.先变长后变短 D.先变短后变长
9.小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为( )
A.上午8时 B.上午9时30分 C.上午10时 D.上午12时
10.圆桌面(桌面中间有一个直径为1m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为2m,桌面离地面1m,若灯泡离地面2m,则地面圆环形阴影的面积是( )
A.2πm2 B.3πm2 C.6πm2 D.12πm2
二、填空题
11.在一盏路灯旁的地面上竖直立着两根木杆,两根木杆在这盏路灯下形成各自的影子,则将它们各自的顶端与自己的影子的顶端连线所形成的两个三角形_____相似.(填“可能”或“不可能”).
12.如图,有一张直径为1.2米的圆桌,其高度为0.8米,同时有一盏灯距地面2米,圆桌在水平地面上的影子是,∥,和是光线,建立如图所示的平面直角坐标系,其中点的坐标是.那么点的坐标是_________.
13.如图,物体在灯泡发出的光照射下形成的影子是_____投影.(填“平行”或“中心”).
14.身高相同的小刚和小美站在一盏路灯下的不同位置,已知小刚的影子比小美长,我们可以判定小刚离灯较________.
15.如图,晚上小红由路灯A走向路灯B,当她走到点P时,发现她的影子顶部正好接触到路灯B的底部,此时她距离路灯A,距离路灯B.如果小红的身高为,那么路灯A的高度是___________m.
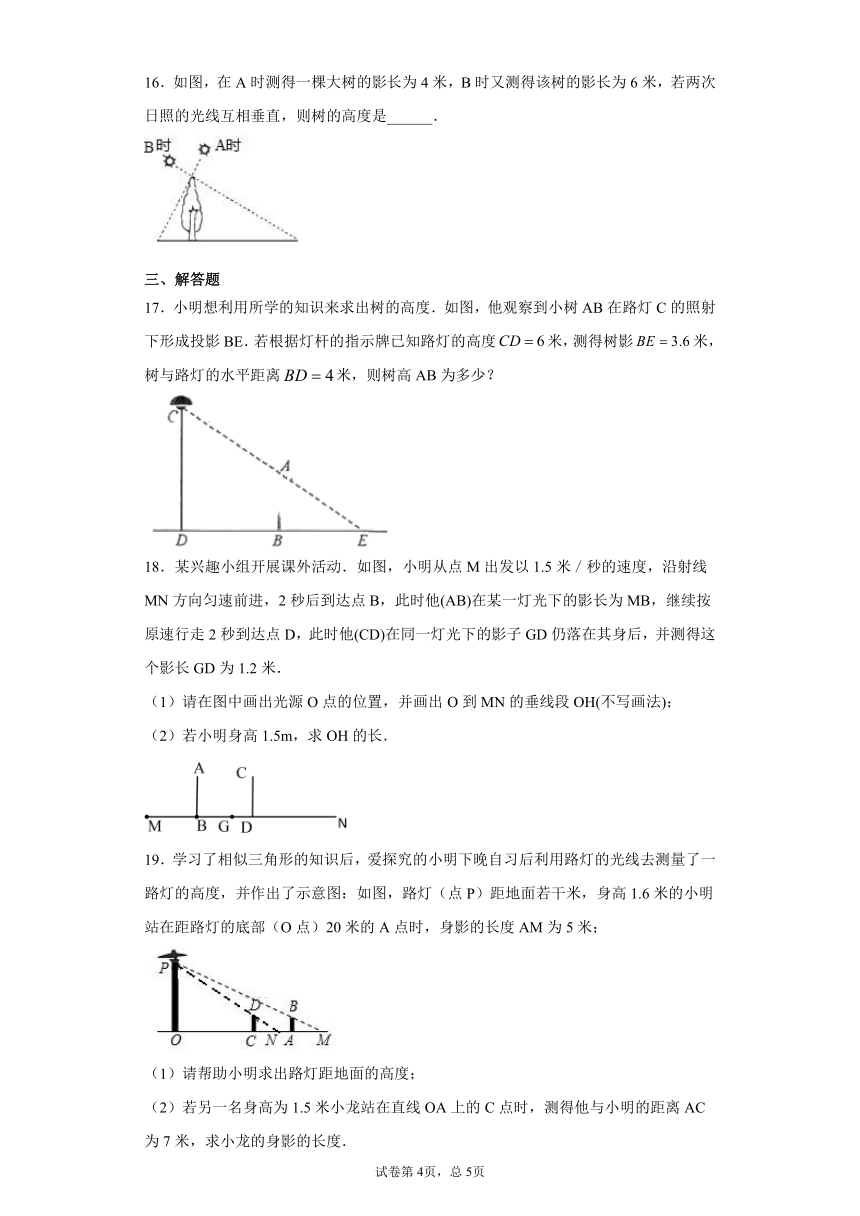
16.如图,在A时测得一棵大树的影长为4米,B时又测得该树的影长为6米,若两次日照的光线互相垂直,则树的高度是______.
三、解答题
17.小明想利用所学的知识来求出树的高度.如图,他观察到小树AB在路灯C的照射下形成投影BE.若根据灯杆的指示牌已知路灯的高度米,测得树影米,树与路灯的水平距离米,则树高AB为多少?
18.某兴趣小组开展课外活动.如图,小明从点M出发以1.5米/秒的速度,沿射线MN方向匀速前进,2秒后到达点B,此时他(AB)在某一灯光下的影长为MB,继续按原速行走2秒到达点D,此时他(CD)在同一灯光下的影子GD仍落在其身后,并测得这个影长GD为1.2米.
(1)请在图中画出光源O点的位置,并画出O到MN的垂线段OH(不写画法);
(2)若小明身高1.5m,求OH的长.
19.学习了相似三角形的知识后,爱探究的小明下晚自习后利用路灯的光线去测量了一路灯的高度,并作出了示意图:如图,路灯(点P)距地面若干米,身高1.6米的小明站在距路灯的底部(O点)20米的A点时,身影的长度AM为5米;
(1)请帮助小明求出路灯距地面的高度;
(2)若另一名身高为1.5米小龙站在直线OA上的C点时,测得他与小明的距离AC为7米,求小龙的身影的长度.
20.如图,王乐同学在晩上由路灯走向路灯.当他行到处时发现,他往路灯下的影长为2m,且恰好位于路灯的正下方,接着他又走了到处,此时他在路灯下的影孑恰好位于路灯的正下方(已知王乐身高,路灯高).
(1)王乐站在处时,在路灯下的影子是哪条线段?
(2)计算王乐站在处时,在路灯下的影长;
(3)计算路灯的高度.
参考答案
1.A
2.D
3.A
4.A
5.A
6.A
7.B
8.D
9.A
10.B
11.可能
12.
13.中心.
14.远
15.6
16.6
17.
【详解】
∵AB∥CD,
∴△EAB∽△ECD,
∴,
∴AB(米).
答:树高AB为米.
18.(1)见解析;(2)4m
【详解】
解:(1)如图所示:
(2)由题意得:BM=BD=2×1.5=3,
∵CD∥OH,
∴△CDG∽△OHG,
∴,
∵AB=CD=1.5,
∴①,
∵AB∥OH,
∴△ABM∽△OHM,
,
∴②,
由①②得:OH=4,
则OH的长为4m.
.
19.(1)路灯距地面的高度为8米;(2)小龙的身影的长度为3米
【详解】
解:(1)∵AB⊥OM,PO⊥OM,
∴,
∴,
∴,
∴OP=8,
即路灯距地面的高度为8米;
(2)∵CD⊥OM,PO⊥OM,
∴,
∴,
∵OC=OA-AC=20-7=13,CD=1.5,OP=8,
∴,
∴CN=3,
即小龙的身影的长度为3米.
20.(1)线段CP为王乐在路灯B下的影子;(2)王乐站在Q处时,在路灯A下的影长为1.5m;(3)路灯A的高度为12m
【详解】
解:(1)线段CP为王乐在路灯B下的影子.
(2)由题意得Rt△CEP∽Rt△CBD,
∴,
解得:QD=1.5m.
所以王乐站在Q处时,在路灯A下的影长为1.5m
(3)由题意得Rt△QDF∽Rt△CDA,
∴,
∴,
解得:AC=12m.
所以路灯A的高度为12m.
一、单选题
1.在小明住的小区有一条笔直的路,路中间有一盏路灯,一天晚上他行走在这条路上如图,当他从点走到点的过程,他在灯光照射下的影长与所走路程的变化关系图象大致是( )
A. B. C. D.
2.如图,在平面直角坐标系中,点是一个光源.木杆AB两端的坐标分别为,.则木杆AB在x轴上的投影长为( ).
A.4 B.5 C.6 D.8
3.一个等边三角形在太阳光的照射下,在地面上的投影不可能是( )
A. B. C. D.
4.如图,晚上小亮在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子( )
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短
5.如图,白炽灯下有一个乒乓球,当乒乓球越接近灯泡时,它在地面上的影子( )
A.越大 B.越小 C.不变 D.无法确定
6.如图,小明夜晚从路灯下A处走到B处这一过程中,他在路上的影子( )
A.逐渐变长 B.逐渐变短
C.长度不变 D.先变短后变长
7.下列哪种光线形成的投影不是中心投影( )
A.台灯 B.太阳 C.手电筒 D.路灯
8.晚上,王老师出去散步,他先走向一盏路灯,然后离路灯而去,他会发现自己的身影是( )
A.变长 B.变短 C.先变长后变短 D.先变短后变长
9.小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为( )
A.上午8时 B.上午9时30分 C.上午10时 D.上午12时
10.圆桌面(桌面中间有一个直径为1m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为2m,桌面离地面1m,若灯泡离地面2m,则地面圆环形阴影的面积是( )
A.2πm2 B.3πm2 C.6πm2 D.12πm2
二、填空题
11.在一盏路灯旁的地面上竖直立着两根木杆,两根木杆在这盏路灯下形成各自的影子,则将它们各自的顶端与自己的影子的顶端连线所形成的两个三角形_____相似.(填“可能”或“不可能”).
12.如图,有一张直径为1.2米的圆桌,其高度为0.8米,同时有一盏灯距地面2米,圆桌在水平地面上的影子是,∥,和是光线,建立如图所示的平面直角坐标系,其中点的坐标是.那么点的坐标是_________.
13.如图,物体在灯泡发出的光照射下形成的影子是_____投影.(填“平行”或“中心”).
14.身高相同的小刚和小美站在一盏路灯下的不同位置,已知小刚的影子比小美长,我们可以判定小刚离灯较________.
15.如图,晚上小红由路灯A走向路灯B,当她走到点P时,发现她的影子顶部正好接触到路灯B的底部,此时她距离路灯A,距离路灯B.如果小红的身高为,那么路灯A的高度是___________m.
16.如图,在A时测得一棵大树的影长为4米,B时又测得该树的影长为6米,若两次日照的光线互相垂直,则树的高度是______.
三、解答题
17.小明想利用所学的知识来求出树的高度.如图,他观察到小树AB在路灯C的照射下形成投影BE.若根据灯杆的指示牌已知路灯的高度米,测得树影米,树与路灯的水平距离米,则树高AB为多少?
18.某兴趣小组开展课外活动.如图,小明从点M出发以1.5米/秒的速度,沿射线MN方向匀速前进,2秒后到达点B,此时他(AB)在某一灯光下的影长为MB,继续按原速行走2秒到达点D,此时他(CD)在同一灯光下的影子GD仍落在其身后,并测得这个影长GD为1.2米.
(1)请在图中画出光源O点的位置,并画出O到MN的垂线段OH(不写画法);
(2)若小明身高1.5m,求OH的长.
19.学习了相似三角形的知识后,爱探究的小明下晚自习后利用路灯的光线去测量了一路灯的高度,并作出了示意图:如图,路灯(点P)距地面若干米,身高1.6米的小明站在距路灯的底部(O点)20米的A点时,身影的长度AM为5米;
(1)请帮助小明求出路灯距地面的高度;
(2)若另一名身高为1.5米小龙站在直线OA上的C点时,测得他与小明的距离AC为7米,求小龙的身影的长度.
20.如图,王乐同学在晩上由路灯走向路灯.当他行到处时发现,他往路灯下的影长为2m,且恰好位于路灯的正下方,接着他又走了到处,此时他在路灯下的影孑恰好位于路灯的正下方(已知王乐身高,路灯高).
(1)王乐站在处时,在路灯下的影子是哪条线段?
(2)计算王乐站在处时,在路灯下的影长;
(3)计算路灯的高度.
参考答案
1.A
2.D
3.A
4.A
5.A
6.A
7.B
8.D
9.A
10.B
11.可能
12.
13.中心.
14.远
15.6
16.6
17.
【详解】
∵AB∥CD,
∴△EAB∽△ECD,
∴,
∴AB(米).
答:树高AB为米.
18.(1)见解析;(2)4m
【详解】
解:(1)如图所示:
(2)由题意得:BM=BD=2×1.5=3,
∵CD∥OH,
∴△CDG∽△OHG,
∴,
∵AB=CD=1.5,
∴①,
∵AB∥OH,
∴△ABM∽△OHM,
,
∴②,
由①②得:OH=4,
则OH的长为4m.
.
19.(1)路灯距地面的高度为8米;(2)小龙的身影的长度为3米
【详解】
解:(1)∵AB⊥OM,PO⊥OM,
∴,
∴,
∴,
∴OP=8,
即路灯距地面的高度为8米;
(2)∵CD⊥OM,PO⊥OM,
∴,
∴,
∵OC=OA-AC=20-7=13,CD=1.5,OP=8,
∴,
∴CN=3,
即小龙的身影的长度为3米.
20.(1)线段CP为王乐在路灯B下的影子;(2)王乐站在Q处时,在路灯A下的影长为1.5m;(3)路灯A的高度为12m
【详解】
解:(1)线段CP为王乐在路灯B下的影子.
(2)由题意得Rt△CEP∽Rt△CBD,
∴,
解得:QD=1.5m.
所以王乐站在Q处时,在路灯A下的影长为1.5m
(3)由题意得Rt△QDF∽Rt△CDA,
∴,
∴,
解得:AC=12m.
所以路灯A的高度为12m.
