18.1.1平行四边形的性质课件(28张)
文档属性
| 名称 | 18.1.1平行四边形的性质课件(28张) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 20:30:17 | ||
图片预览







文档简介
18.1.1 平行四边形的性质
第十八章 平行四边形
1、四边形的内角和为_____, 外角和为_____.
2、已知:a∥b,c∥d,则
⑴ ∠1=∠2( )
∠2=∠3( )
⑵ ∠1+∠4=___ ( )
∠3+∠4=___ ( )
∴∠1=∠3 ( )
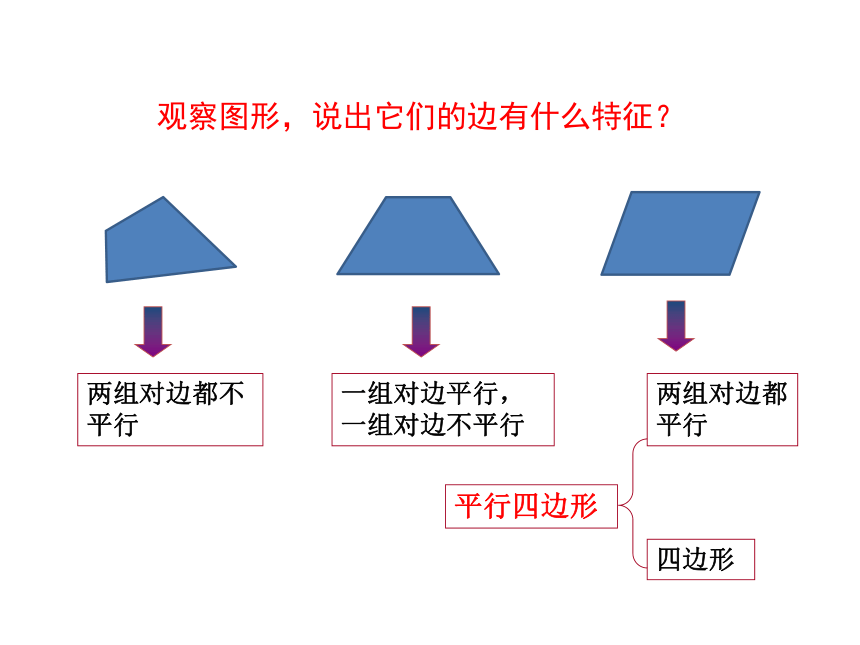
两组对边都不平行
一组对边平行,一组对边不平行
两组对边都平行
四边形
平行四边形
观察图形,说出它们的边有什么特征?
1、理解平行四边形的概念定义;
2、探索并掌握平行四边形对边相等、对角相等等性质,并根据性质进行简单的推理;
3、理解掌握两平行线之间的距离的概念及性质.
你能举出生活中常见的一些含有平行四边形的事例吗?
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD(注意顺序)
平行四边形
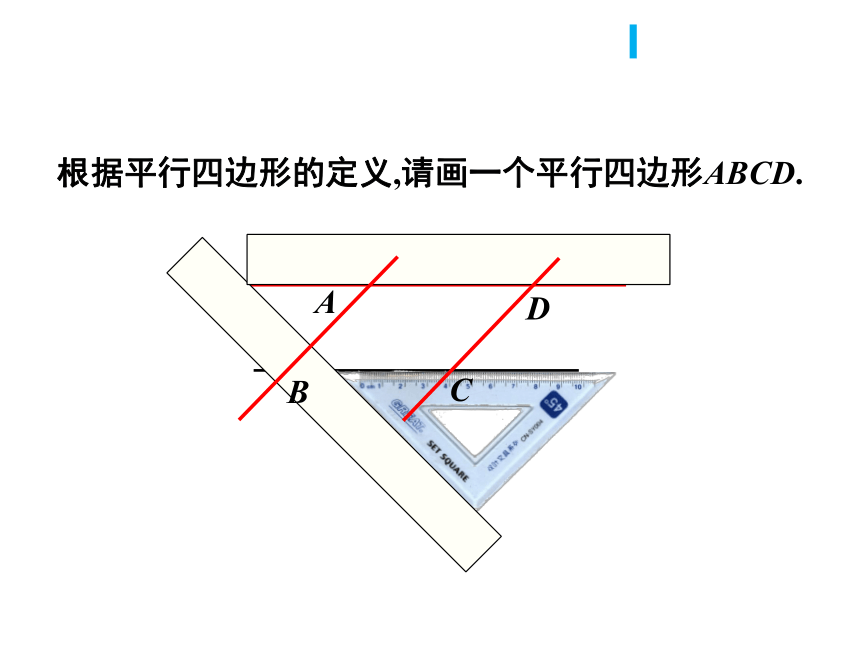
根据平行四边形的定义,请画一个平行四边形ABCD.
D
A
B
C
几何语言:
∵四边形ABCD是平行四边形
∴四边形ABCD是平行四边形
AB∥CD,
AD∥BC
∴
AB∥CD,
AD∥BC
∵
A
D
B
C
平行四边形
对边分别平行的四边形
对平行四边形的理解
A
B
C
D
平行四边形相关概念
平行四边形相对的边称为对边, 相对的角称为对角.
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA;
∠BAD与∠DCB.
如图,EF∥BC∥AD, GH∥AB∥CD, EF与GH相交于点O,则图中共有___个平行四边形.
A
O
H
F
E
D
C
B
G
找一找
9
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
拼一拼
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题.
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
A
B
C
D
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠4=∠3
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
平行四边形的性质定理
几何语言:
A
D
B
C
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
几何语言:
A
B
C
D
E
F
例1 如图,在□ABCD中,DE⊥AB,BF ⊥CD,垂足分别为E、F.
求证: AE=CF
证明:
∵ 四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB.
又∠ADE=∠CFB=90°
∴ △ ADE≌ △ CBF.
∴ AE=CF
如图,直线a∥b,A,B为直线a上的任意两点,点A 到直线b 的距离和点B 到直线b 的距离相等吗?
相等
A
B
C
D
b
a
你能够证明出来吗?
求证:(1)夹在两平行直线间的平行线段相等.
(2)如果两条直线平行,那么一条直线上各点到另一条直线的距离相等.
(1)已知:如图, , A,D是直线 上的任意两点,过点 A,D 作 , 分别交 于点B, C.
求证:AB=CD
证明:
(平行四边形定义)
(平行四边形的性质定理1)
已知:如图, ,A,D是直线 上的任意两点,AB ,
垂足是B, DC ,垂足是C.
求证:AB=CD
证明:
(2)求证:如果两条直线平行,那么一条直线上各点到另一条直线的距离相等.
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
两条平行线之间的距离
B
A
a
b
如图,直线a∥b,A是直线a上的任意一点,AB ⊥b ,B是垂足,线段AB的长就是a、b之间的距离.
1.如图,在
若∠A=130°,则∠B=______ 、∠C=______ 、∠D=______
ABCD中,
A:基础知识:
B:变式训练:
(1)若∠A+ ∠C= 200°,则∠A=______ 、∠B=______
(2)若∠A:∠B= 5:4,则∠C=______ 、∠D=______
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
C:拓展延伸:
如图,在
ABCD中,
1、∠A:∠B: ∠C :∠D的度数可能是( )
A、1:2:3:4 B、3:2:3:2
C、2:3:3:2 D、2:2:3:3
C
D
A
B
2、连接AC, 若∠D=80°, ∠DAC=40°则, ∠B=_____,
∠BAC=______.
B
80°
60°
P43,练习第1、2题.
作 业
本节课主要学习了哪些知识?
1、本节课研究了什么图形的性质?
2、什么是平行四边形?
3、平行四边形有哪些性质?
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
4、什么是两条平行线之间的距离?
判断题(对的在括号内填“√”,错的填“×”):
(1)平行四边形两组对边分别平行且相等. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°. ( )
(4)如果平行四边形相邻两边长分别是2cm和
3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=42°,
那么∠B=48°. ( )
(6)在平行四边形ABCD中,如果∠A=35°,
那么∠C=145°. ( )
√
√
√
×
×
×
当堂练习
如图,在 ABCD中.
(1)若∠A =32。,求其余三个角的度数.
A
B
C
D
∵四边形ABCD是平行四边形,
解:
且 ∠A =32。(已知),
∴ ∠A = ∠C=32。, ∠B= ∠D (平行四边形的对角相等).
又∵AD∥BC(平行四边形的对边平行),
∴ ∠A + ∠B =180。(两直线平行,同旁内角互补),
∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。.
例2
典例解析
(2)连结AC,已知 ABCD的周长等于20 cm,AC=
7cm,求△ABC的周长.
解:∵四边形ABCD是平行四边形(已知),
∴AB=CD,BC=AD(平行四边形的对边相等).
又∵AB+BC+CD+AD=20cm(已知),
∴AB+BC= 10cm.
∵AC=7cm,
∴ △ABC的周长为AB+BC+AC= 17cm.
A
B
C
D
典例解析
1.如图,在□ABCD中.
(1)若∠A=130°,则∠B=______ ,∠C=______ ,
∠D=______.
(3)若∠A+ ∠C= 200°,则∠A=_____,∠B=______.
(2)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
16
练一练
2.如图,在平行四边形ABCD中,若AE平分∠DAB,
AB=5cm, AD=9cm,则EC= .
C
4cm
A
B
D
E
第十八章 平行四边形
1、四边形的内角和为_____, 外角和为_____.
2、已知:a∥b,c∥d,则
⑴ ∠1=∠2( )
∠2=∠3( )
⑵ ∠1+∠4=___ ( )
∠3+∠4=___ ( )
∴∠1=∠3 ( )
两组对边都不平行
一组对边平行,一组对边不平行
两组对边都平行
四边形
平行四边形
观察图形,说出它们的边有什么特征?
1、理解平行四边形的概念定义;
2、探索并掌握平行四边形对边相等、对角相等等性质,并根据性质进行简单的推理;
3、理解掌握两平行线之间的距离的概念及性质.
你能举出生活中常见的一些含有平行四边形的事例吗?
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD(注意顺序)
平行四边形
根据平行四边形的定义,请画一个平行四边形ABCD.
D
A
B
C
几何语言:
∵四边形ABCD是平行四边形
∴四边形ABCD是平行四边形
AB∥CD,
AD∥BC
∴
AB∥CD,
AD∥BC
∵
A
D
B
C
平行四边形
对边分别平行的四边形
对平行四边形的理解
A
B
C
D
平行四边形相关概念
平行四边形相对的边称为对边, 相对的角称为对角.
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA;
∠BAD与∠DCB.
如图,EF∥BC∥AD, GH∥AB∥CD, EF与GH相交于点O,则图中共有___个平行四边形.
A
O
H
F
E
D
C
B
G
找一找
9
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
拼一拼
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题.
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
A
B
C
D
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠4=∠3
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
平行四边形的性质定理
几何语言:
A
D
B
C
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
几何语言:
A
B
C
D
E
F
例1 如图,在□ABCD中,DE⊥AB,BF ⊥CD,垂足分别为E、F.
求证: AE=CF
证明:
∵ 四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB.
又∠ADE=∠CFB=90°
∴ △ ADE≌ △ CBF.
∴ AE=CF
如图,直线a∥b,A,B为直线a上的任意两点,点A 到直线b 的距离和点B 到直线b 的距离相等吗?
相等
A
B
C
D
b
a
你能够证明出来吗?
求证:(1)夹在两平行直线间的平行线段相等.
(2)如果两条直线平行,那么一条直线上各点到另一条直线的距离相等.
(1)已知:如图, , A,D是直线 上的任意两点,过点 A,D 作 , 分别交 于点B, C.
求证:AB=CD
证明:
(平行四边形定义)
(平行四边形的性质定理1)
已知:如图, ,A,D是直线 上的任意两点,AB ,
垂足是B, DC ,垂足是C.
求证:AB=CD
证明:
(2)求证:如果两条直线平行,那么一条直线上各点到另一条直线的距离相等.
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
两条平行线之间的距离
B
A
a
b
如图,直线a∥b,A是直线a上的任意一点,AB ⊥b ,B是垂足,线段AB的长就是a、b之间的距离.
1.如图,在
若∠A=130°,则∠B=______ 、∠C=______ 、∠D=______
ABCD中,
A:基础知识:
B:变式训练:
(1)若∠A+ ∠C= 200°,则∠A=______ 、∠B=______
(2)若∠A:∠B= 5:4,则∠C=______ 、∠D=______
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
C:拓展延伸:
如图,在
ABCD中,
1、∠A:∠B: ∠C :∠D的度数可能是( )
A、1:2:3:4 B、3:2:3:2
C、2:3:3:2 D、2:2:3:3
C
D
A
B
2、连接AC, 若∠D=80°, ∠DAC=40°则, ∠B=_____,
∠BAC=______.
B
80°
60°
P43,练习第1、2题.
作 业
本节课主要学习了哪些知识?
1、本节课研究了什么图形的性质?
2、什么是平行四边形?
3、平行四边形有哪些性质?
性质定理1:平行四边形的对边相等.
性质定理2:平行四边形的对角相等.
4、什么是两条平行线之间的距离?
判断题(对的在括号内填“√”,错的填“×”):
(1)平行四边形两组对边分别平行且相等. ( )
(2)平行四边形的四个内角都相等. ( )
(3)平行四边形的相邻两个内角的和等于180°. ( )
(4)如果平行四边形相邻两边长分别是2cm和
3cm,那么周长是10cm. ( )
(5)在平行四边形ABCD中,如果∠A=42°,
那么∠B=48°. ( )
(6)在平行四边形ABCD中,如果∠A=35°,
那么∠C=145°. ( )
√
√
√
×
×
×
当堂练习
如图,在 ABCD中.
(1)若∠A =32。,求其余三个角的度数.
A
B
C
D
∵四边形ABCD是平行四边形,
解:
且 ∠A =32。(已知),
∴ ∠A = ∠C=32。, ∠B= ∠D (平行四边形的对角相等).
又∵AD∥BC(平行四边形的对边平行),
∴ ∠A + ∠B =180。(两直线平行,同旁内角互补),
∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。.
例2
典例解析
(2)连结AC,已知 ABCD的周长等于20 cm,AC=
7cm,求△ABC的周长.
解:∵四边形ABCD是平行四边形(已知),
∴AB=CD,BC=AD(平行四边形的对边相等).
又∵AB+BC+CD+AD=20cm(已知),
∴AB+BC= 10cm.
∵AC=7cm,
∴ △ABC的周长为AB+BC+AC= 17cm.
A
B
C
D
典例解析
1.如图,在□ABCD中.
(1)若∠A=130°,则∠B=______ ,∠C=______ ,
∠D=______.
(3)若∠A+ ∠C= 200°,则∠A=_____,∠B=______.
(2)若AB=3,BC=5,则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
16
练一练
2.如图,在平行四边形ABCD中,若AE平分∠DAB,
AB=5cm, AD=9cm,则EC= .
C
4cm
A
B
D
E
