18.1.1 平行四边形的性质课件 (18张)
文档属性
| 名称 | 18.1.1 平行四边形的性质课件 (18张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 00:00:00 | ||
图片预览




文档简介
18.1.1 平行四边形的性质
生活中的平行四边形
老师:小明,你能用一根28cm的绳子围成一边为6cm的平行四边形吗?
问题情境:
1.理解平行四边形的概念;
2.探索并掌握平行四边形对边相等、对角相等的性质;
3.初步体会几何研究的一般思路与方法。
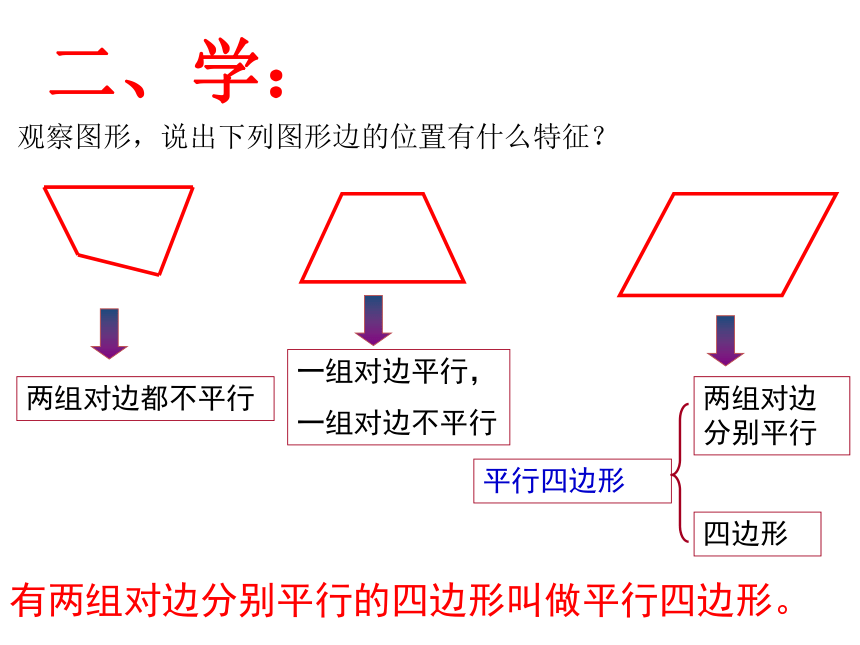
一、明:
学习目标
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
有两组对边分别平行的四边形叫做平行四边形。
观察图形,说出下列图形边的位置有什么特征?
二、学:
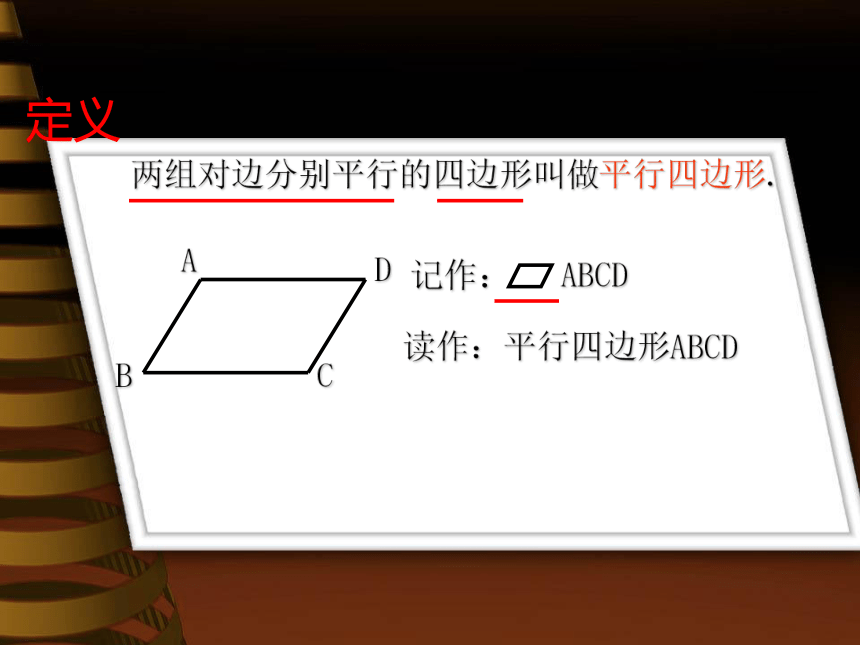
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
定义
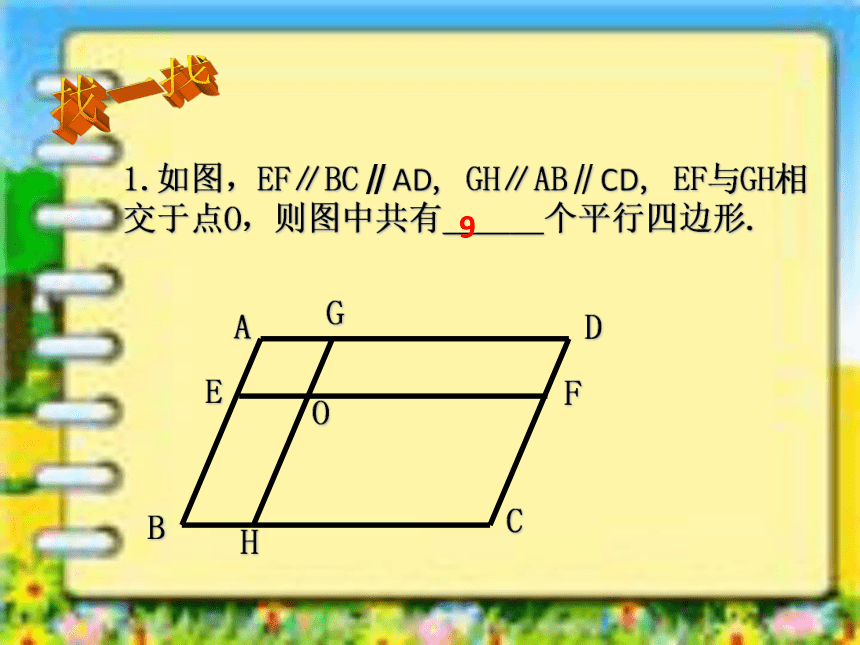
1.如图,EF∥BC∥AD, GH∥AB∥CD, EF与GH相交于点O,则图中共有___个平行四边形.
A
O
H
F
E
D
C
B
G
找一找
9
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
拼一拼
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题。
平行四边形的对边、对角有怎样的数量大小关系?
A
B
C
D
猜一猜
平行四边形的对边相等.
平行四边形的对角相等.
.
请用直尺,量角器等工具度量你手中拼好的平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确?
量一量
A
B
C
D
用你以前所学的知识证明猜想.
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
A
B
C
D
证一证
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
平行四边形的对边平行.
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的性质
A
B
C
D
例1 如图,在□ABCD中
(1)若∠A=130°,则∠B=______ ,∠C=______ , ∠D=______。
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,
则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,
则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
16
(1)平行四边形的对角相等;(2)平行四边形的
邻角互补;(3)平行四边形的一组邻边之和等于周长的一半,反之,周长=2倍邻边之和.
归纳
三、查:
例2:如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC的长以及 ABCD的面积.
8
10
B
C
D
A
●
O
解:
∴△ABC是直角三角形
又∵AC⊥BC
∵四边形ABCD是平行四形
∴BC=AD=8,CD=AB=10
∴
∴S = BC×AC=8×6=48
ABCD
3.有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解:∵AE//BC,AB//CF,
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°,
AD=BC=60cm.
∴ED=AD-AE=80-60=20cm.
答:DE的长度是20cm, ∠D的度数是60°.
几 何 语 言
边
角
文字叙述
对边平行
对边相等
对角相等
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
平行四边形的性质
A
B
C
D
四、教:
A
B
C
D
1、若 的周长是30㎝,AB :CB=3 :2,
则AD= ㎝,CD= ㎝.
ABCD
2、
中,如果∠B的外角是 50°,那么平行四边形的每个内角是多少度?
ABCD
五、练:
作业:
1、教材43页 练习 1题;
2、教材49页 复习巩固 1题;
生活中的平行四边形
老师:小明,你能用一根28cm的绳子围成一边为6cm的平行四边形吗?
问题情境:
1.理解平行四边形的概念;
2.探索并掌握平行四边形对边相等、对角相等的性质;
3.初步体会几何研究的一般思路与方法。
一、明:
学习目标
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
有两组对边分别平行的四边形叫做平行四边形。
观察图形,说出下列图形边的位置有什么特征?
二、学:
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
定义
1.如图,EF∥BC∥AD, GH∥AB∥CD, EF与GH相交于点O,则图中共有___个平行四边形.
A
O
H
F
E
D
C
B
G
找一找
9
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
拼一拼
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连接对角线转化为两个全等的三角形进行解题。
平行四边形的对边、对角有怎样的数量大小关系?
A
B
C
D
猜一猜
平行四边形的对边相等.
平行四边形的对角相等.
.
请用直尺,量角器等工具度量你手中拼好的平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确?
量一量
A
B
C
D
用你以前所学的知识证明猜想.
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
A
B
C
D
证一证
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
平行四边形的对边平行.
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的性质
A
B
C
D
例1 如图,在□ABCD中
(1)若∠A=130°,则∠B=______ ,∠C=______ , ∠D=______。
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,
则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,
则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
16
(1)平行四边形的对角相等;(2)平行四边形的
邻角互补;(3)平行四边形的一组邻边之和等于周长的一半,反之,周长=2倍邻边之和.
归纳
三、查:
例2:如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC的长以及 ABCD的面积.
8
10
B
C
D
A
●
O
解:
∴△ABC是直角三角形
又∵AC⊥BC
∵四边形ABCD是平行四形
∴BC=AD=8,CD=AB=10
∴
∴S = BC×AC=8×6=48
ABCD
3.有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解:∵AE//BC,AB//CF,
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°,
AD=BC=60cm.
∴ED=AD-AE=80-60=20cm.
答:DE的长度是20cm, ∠D的度数是60°.
几 何 语 言
边
角
文字叙述
对边平行
对边相等
对角相等
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
平行四边形的性质
A
B
C
D
四、教:
A
B
C
D
1、若 的周长是30㎝,AB :CB=3 :2,
则AD= ㎝,CD= ㎝.
ABCD
2、
中,如果∠B的外角是 50°,那么平行四边形的每个内角是多少度?
ABCD
五、练:
作业:
1、教材43页 练习 1题;
2、教材49页 复习巩固 1题;
