18.2.1正方形的判定课件(18张)
文档属性
| 名称 | 18.2.1正方形的判定课件(18张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 361.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 20:36:28 | ||
图片预览


文档简介
第十八章 平行四边形
导入新课
讲授新课
当堂练习
课堂小结
学练优八年级数学下(RJ)
教学课件
18.2.3 正方形
第2课时 正方形的判定
问题1 正方形有哪些性质?
A
B
C
D
O
导入新课
复习引入
正方形的性质
对边平行
四条边相等
四个角都是直角
互相垂直
边
角
对角线
每一条对角线平分一组对角
互相平分
相等
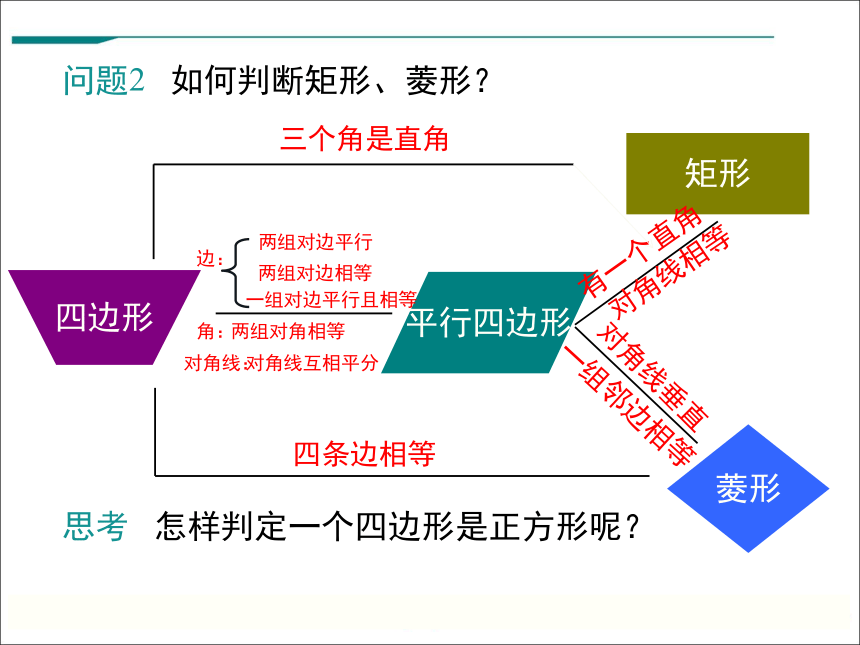
问题2 如何判断矩形、菱形?
平行四边形
矩形
菱形
四边形
三个角是直角
四条边相等
边:
有一个直角
对角线相等
一组邻边相等
对角线垂直
思考 怎样判定一个四边形是正方形呢?
两组对边平行
两组对边相等
一组对边平行且相等
角:
两组对角相等
对角线:
对角线互相平分
矩形
菱形
正
方
形
平行四边形
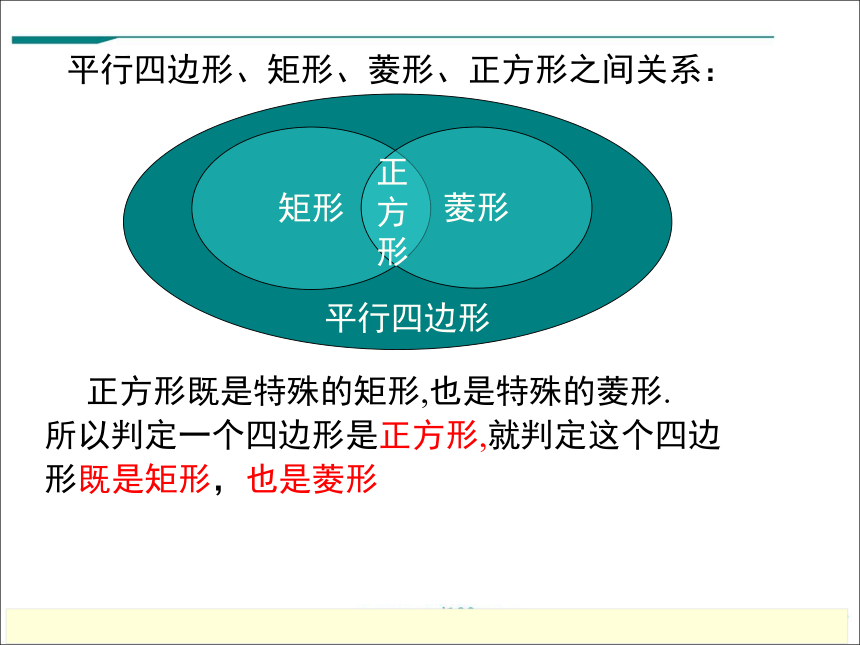
正方形既是特殊的矩形,也是特殊的菱形.
所以判定一个四边形是正方形,就判定这个四边
形既是矩形,也是菱形
平行四边形、矩形、菱形、正方形之间关系:
讲授新课
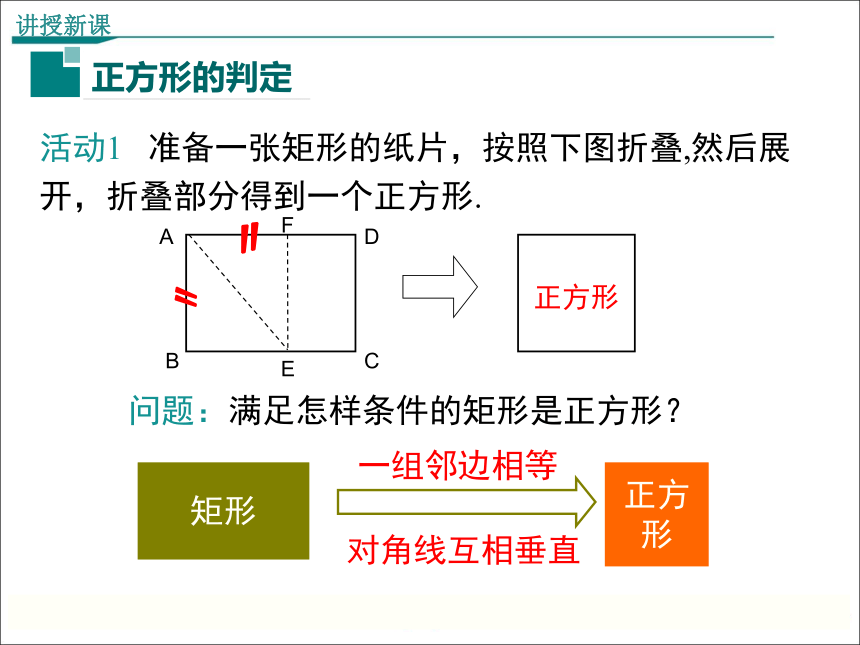
正方形的判定
活动1 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形.
正方形
问题:满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
对角线互相垂直
〃
〃
A
B
C
D
E
F
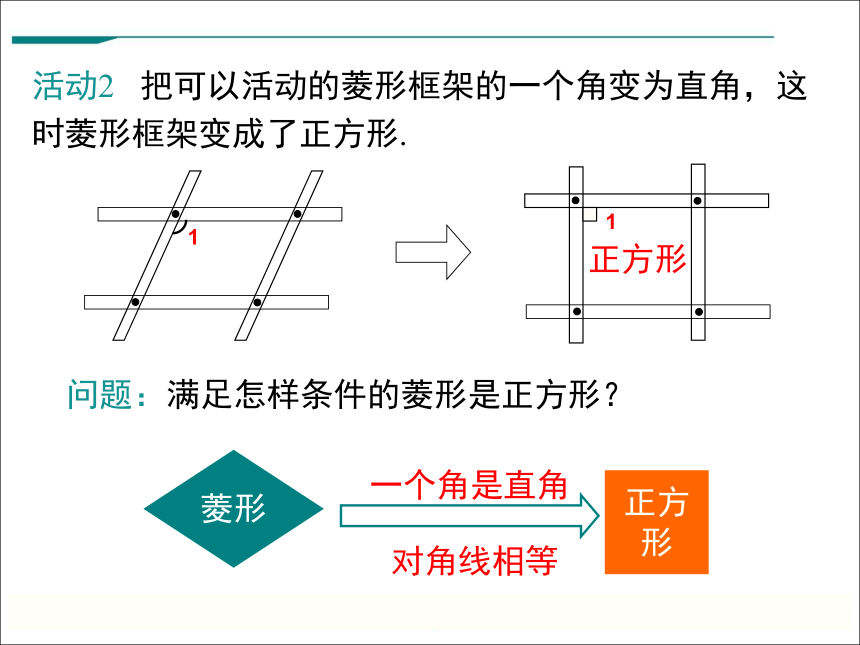
活动2 把可以活动的菱形框架的一个角变为直角,这时菱形框架变成了正方形.
正方形
菱形
问题:满足怎样条件的菱形是正方形?
正方形
一个角是直角
对角线相等
1
1
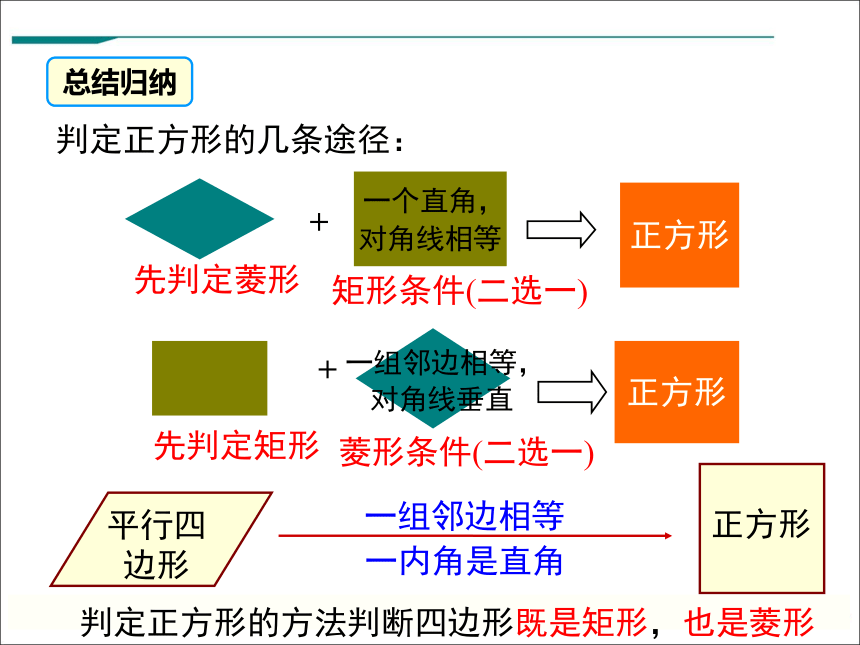
判定正方形的几条途径:
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件(二选一)
菱形条件(二选一)
一个直角,
一组邻边相等,
总结归纳
对角线相等
对角线垂直
平行四边形
正方形
一组邻边相等
一内角是直角
判定正方形的方法判断四边形既是矩形,也是菱形
典型例题1:如图,在Rt△ABC中,∠C=90°,∠A、∠B的平分线交于点D.DE⊥BC,DF⊥AC.求证:四边形CEDF为正方形.
N
证明:
过点D作DN⊥AB,垂足为N
∵∠C=90°,DE⊥BC,DF⊥AC
∴∠C=∠DFC=∠DEC=90°
∴四边形DFCE是矩形
∵AD平分∠FAN,DF⊥AC,DN⊥AB
∴DF=DN
∵BD平分∠EBN,DE⊥BC,DN⊥AB
∴DE=DN
∴DF=DE
∴四边形CEDF是正方形
典型例题2:如图,正方形ABCD的边长为8cm,点E,F,G,H分别是AB,BC,CD,DA边上的动点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形;
(2)求四边形EFGH面积的最小值.
证明(1):
∵四边形ABCD是正方形
∴∠A=∠B=90°,AB=AD
∵AE=DH=BF
∴AH=BE
在△AEH和△BFE中
∴△AEH≌△BFE(SAS)
∴EH=EF
同理:EH=EF=FG=GH
∴四边形EFGH是菱形
∵∠A=90°
∴∠AEH+∠BEF=90°
∴∠HEF=90°
∴四边形EFGH是正方形
∴∠AHE+∠AEH=90°
∵△AEH≌△BFE
∴∠AHE=∠BEF
典型例题2:如图,正方形ABCD的边长为8cm,点E,F,G,H分别是AB,BC,CD,DA边上的动点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形;
(2)求四边形EFGH面积的最小值.
证明(1):
∵四边形ABCD是正方形
∴∠A=∠B=90°,AB=AD
∵AE=DH=BF
∴AH=BE
在△AEH和△BFE中
∴△AEH≌△BFE(SAS)
∴∠AHE=∠BEF
同理:∠EFG=∠FGH=∠HEF=90°
∴四边形EFGH是矩形
∴∠AEH+∠BEF=90°
∴∠HEF=90°
∴四边形EFGH是正方形
∵∠A=90°
∴∠AHE+∠AEH=90°
∵△AEH≌△BFE
∴EH=EF
典型例题2:如图,正方形ABCD的边长为8cm,点E,F,G,H分别是AB,BC,CD,DA边上的动点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形;
(2)求四边形EFGH面积的最小值.
解(2):
设四边形EFGH面积为S,BE=xcm,则BF=(8﹣x)cm
在Rt△BEF中,由勾股定理得:
EF2=BE2+BF2=x2+(8﹣x)2
∴S=x2+(8﹣x)2=2x2-16x+64
=2(x2﹣8x)+64
=2(x﹣4)2+32
∵2(x﹣4)2≥0
∴S有最小值
当x=4时,S最小值=32
∴四边形EFGH面积的最小值为32cm2.
=2(x2﹣8x+16-16)+64
=2(x2﹣8x+16)-32+64
拓展延伸1:如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A,D,G在同一条直线,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H,求线段AH的长.
解:
∵四边形ABCD和四边形DEFG为正方形
∴AD=CD,DG=DE,∠ADE=∠CDG=90°
在△GDC和△EDA中
∴△GDC≌△EDA(SAS)
∴∠GCD=∠EAD
∵AD=3,DE=1
在Rt△CDG中,
由勾股定理得:
∴CD=3,DG=1
∵∠ADE=90°
∴∠HEC+∠EHC=90°
∴∠EHC=90°
∴∠DAE+∠AED=90°
∵∠DEA=∠CEH
∵∠AHC=90°
∴AG=AD+DG=4
拓展延伸1:如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A,D,G在同一条直线,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H,求线段AH的长.
解:
∵四边形ABCD和四边形DEFG为正方形
∴AD=CD,DG=DE,∠ADE=∠CDG=90°
在△GDC和△EDA中
∴△GDC≌△EDA(SAS)
∴∠GCD=∠EAD
∵AD=3,DE=1
在Rt△CDG中,由勾股定理得:
∴CD=3,DG=1
∵∠ADE=90°
∴∠HEC+∠EHC=90°
∴∠EHC=90°
∴∠DAE+∠AED=90°
∵∠DEA=∠CEH
∴AG=AD+DG=4
∵四边形ABCD为正方形
∴AB=BC=3,∠B=90°
∵∠EHC=90°
∴∠AHC=∠AHG=90°
拓展延伸2:如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'CD'处,B'C'与CD相交于点M,求点M的坐标.
解:连接AM
∵将边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB'C′D′
∴AD=AB=AB′=1,
∴∠B′AD=∠BAD-∠BAB′=60°
在Rt△ADM和Rt△AB′M中
∴Rt△ADM≌Rt△AB′M(HL)
∴∠DAM=∠B′AM=30°
在Rt△ADM中,∠DAM=30°
AM=2DM
设DM=x,则AM=2x
在Rt△ADM中,由勾股定理得
∴x2+12=(2x)2
AD2+MD2=AM2
∠BAB′=30°,
∠BAD=∠ADC=∠ABC=∠B′=90°
课堂小结
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
课堂小结
谈一谈本节课
你的收获是什么?
已知:如图,在矩形ABCD中,AC , DB是它的两条对角线,
AC⊥DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴ AO=CO=BO=DO ,∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
证一证
A
B
C
D
O
对角线互相垂直的矩形是正方形.
已知:如图,在菱形ABCD中,AC , DB是它的两条对角线,
AC=DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴四边形ABCD是正方形.
证一证
A
B
C
D
O
对角线相等的菱形是正方形.
导入新课
讲授新课
当堂练习
课堂小结
学练优八年级数学下(RJ)
教学课件
18.2.3 正方形
第2课时 正方形的判定
问题1 正方形有哪些性质?
A
B
C
D
O
导入新课
复习引入
正方形的性质
对边平行
四条边相等
四个角都是直角
互相垂直
边
角
对角线
每一条对角线平分一组对角
互相平分
相等
问题2 如何判断矩形、菱形?
平行四边形
矩形
菱形
四边形
三个角是直角
四条边相等
边:
有一个直角
对角线相等
一组邻边相等
对角线垂直
思考 怎样判定一个四边形是正方形呢?
两组对边平行
两组对边相等
一组对边平行且相等
角:
两组对角相等
对角线:
对角线互相平分
矩形
菱形
正
方
形
平行四边形
正方形既是特殊的矩形,也是特殊的菱形.
所以判定一个四边形是正方形,就判定这个四边
形既是矩形,也是菱形
平行四边形、矩形、菱形、正方形之间关系:
讲授新课
正方形的判定
活动1 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形.
正方形
问题:满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
对角线互相垂直
〃
〃
A
B
C
D
E
F
活动2 把可以活动的菱形框架的一个角变为直角,这时菱形框架变成了正方形.
正方形
菱形
问题:满足怎样条件的菱形是正方形?
正方形
一个角是直角
对角线相等
1
1
判定正方形的几条途径:
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件(二选一)
菱形条件(二选一)
一个直角,
一组邻边相等,
总结归纳
对角线相等
对角线垂直
平行四边形
正方形
一组邻边相等
一内角是直角
判定正方形的方法判断四边形既是矩形,也是菱形
典型例题1:如图,在Rt△ABC中,∠C=90°,∠A、∠B的平分线交于点D.DE⊥BC,DF⊥AC.求证:四边形CEDF为正方形.
N
证明:
过点D作DN⊥AB,垂足为N
∵∠C=90°,DE⊥BC,DF⊥AC
∴∠C=∠DFC=∠DEC=90°
∴四边形DFCE是矩形
∵AD平分∠FAN,DF⊥AC,DN⊥AB
∴DF=DN
∵BD平分∠EBN,DE⊥BC,DN⊥AB
∴DE=DN
∴DF=DE
∴四边形CEDF是正方形
典型例题2:如图,正方形ABCD的边长为8cm,点E,F,G,H分别是AB,BC,CD,DA边上的动点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形;
(2)求四边形EFGH面积的最小值.
证明(1):
∵四边形ABCD是正方形
∴∠A=∠B=90°,AB=AD
∵AE=DH=BF
∴AH=BE
在△AEH和△BFE中
∴△AEH≌△BFE(SAS)
∴EH=EF
同理:EH=EF=FG=GH
∴四边形EFGH是菱形
∵∠A=90°
∴∠AEH+∠BEF=90°
∴∠HEF=90°
∴四边形EFGH是正方形
∴∠AHE+∠AEH=90°
∵△AEH≌△BFE
∴∠AHE=∠BEF
典型例题2:如图,正方形ABCD的边长为8cm,点E,F,G,H分别是AB,BC,CD,DA边上的动点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形;
(2)求四边形EFGH面积的最小值.
证明(1):
∵四边形ABCD是正方形
∴∠A=∠B=90°,AB=AD
∵AE=DH=BF
∴AH=BE
在△AEH和△BFE中
∴△AEH≌△BFE(SAS)
∴∠AHE=∠BEF
同理:∠EFG=∠FGH=∠HEF=90°
∴四边形EFGH是矩形
∴∠AEH+∠BEF=90°
∴∠HEF=90°
∴四边形EFGH是正方形
∵∠A=90°
∴∠AHE+∠AEH=90°
∵△AEH≌△BFE
∴EH=EF
典型例题2:如图,正方形ABCD的边长为8cm,点E,F,G,H分别是AB,BC,CD,DA边上的动点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形;
(2)求四边形EFGH面积的最小值.
解(2):
设四边形EFGH面积为S,BE=xcm,则BF=(8﹣x)cm
在Rt△BEF中,由勾股定理得:
EF2=BE2+BF2=x2+(8﹣x)2
∴S=x2+(8﹣x)2=2x2-16x+64
=2(x2﹣8x)+64
=2(x﹣4)2+32
∵2(x﹣4)2≥0
∴S有最小值
当x=4时,S最小值=32
∴四边形EFGH面积的最小值为32cm2.
=2(x2﹣8x+16-16)+64
=2(x2﹣8x+16)-32+64
拓展延伸1:如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A,D,G在同一条直线,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H,求线段AH的长.
解:
∵四边形ABCD和四边形DEFG为正方形
∴AD=CD,DG=DE,∠ADE=∠CDG=90°
在△GDC和△EDA中
∴△GDC≌△EDA(SAS)
∴∠GCD=∠EAD
∵AD=3,DE=1
在Rt△CDG中,
由勾股定理得:
∴CD=3,DG=1
∵∠ADE=90°
∴∠HEC+∠EHC=90°
∴∠EHC=90°
∴∠DAE+∠AED=90°
∵∠DEA=∠CEH
∵∠AHC=90°
∴AG=AD+DG=4
拓展延伸1:如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A,D,G在同一条直线,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H,求线段AH的长.
解:
∵四边形ABCD和四边形DEFG为正方形
∴AD=CD,DG=DE,∠ADE=∠CDG=90°
在△GDC和△EDA中
∴△GDC≌△EDA(SAS)
∴∠GCD=∠EAD
∵AD=3,DE=1
在Rt△CDG中,由勾股定理得:
∴CD=3,DG=1
∵∠ADE=90°
∴∠HEC+∠EHC=90°
∴∠EHC=90°
∴∠DAE+∠AED=90°
∵∠DEA=∠CEH
∴AG=AD+DG=4
∵四边形ABCD为正方形
∴AB=BC=3,∠B=90°
∵∠EHC=90°
∴∠AHC=∠AHG=90°
拓展延伸2:如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'CD'处,B'C'与CD相交于点M,求点M的坐标.
解:连接AM
∵将边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB'C′D′
∴AD=AB=AB′=1,
∴∠B′AD=∠BAD-∠BAB′=60°
在Rt△ADM和Rt△AB′M中
∴Rt△ADM≌Rt△AB′M(HL)
∴∠DAM=∠B′AM=30°
在Rt△ADM中,∠DAM=30°
AM=2DM
设DM=x,则AM=2x
在Rt△ADM中,由勾股定理得
∴x2+12=(2x)2
AD2+MD2=AM2
∠BAB′=30°,
∠BAD=∠ADC=∠ABC=∠B′=90°
课堂小结
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
课堂小结
谈一谈本节课
你的收获是什么?
已知:如图,在矩形ABCD中,AC , DB是它的两条对角线,
AC⊥DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴ AO=CO=BO=DO ,∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
证一证
A
B
C
D
O
对角线互相垂直的矩形是正方形.
已知:如图,在菱形ABCD中,AC , DB是它的两条对角线,
AC=DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴四边形ABCD是正方形.
证一证
A
B
C
D
O
对角线相等的菱形是正方形.
