18.2.1正方形的性质课件(25张)
图片预览



文档简介
18.2.3 正方形
第十八章 平行四边形
导入新课
讲授新课
当堂练习
课堂小结
学练优八年级数学下(RJ)
教学课件
第1课时 正方形的性质
导入新课
正方形是我们熟悉的几何图形,在生活中无处不在,观察下面图形中的正方形。
情景引入
讲授新课
矩 形
〃
〃
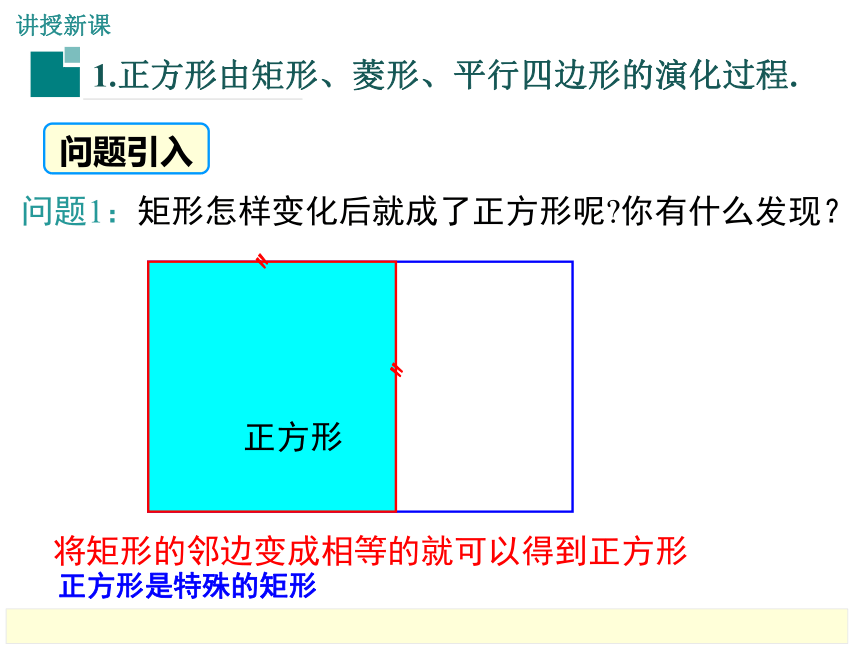
问题1:矩形怎样变化后就成了正方形呢?你有什么发现?
问题引入
正方形
1.正方形由矩形、菱形、平行四边形的演化过程.
将矩形的邻边变成相等的就可以得到正方形
正方形是特殊的矩形
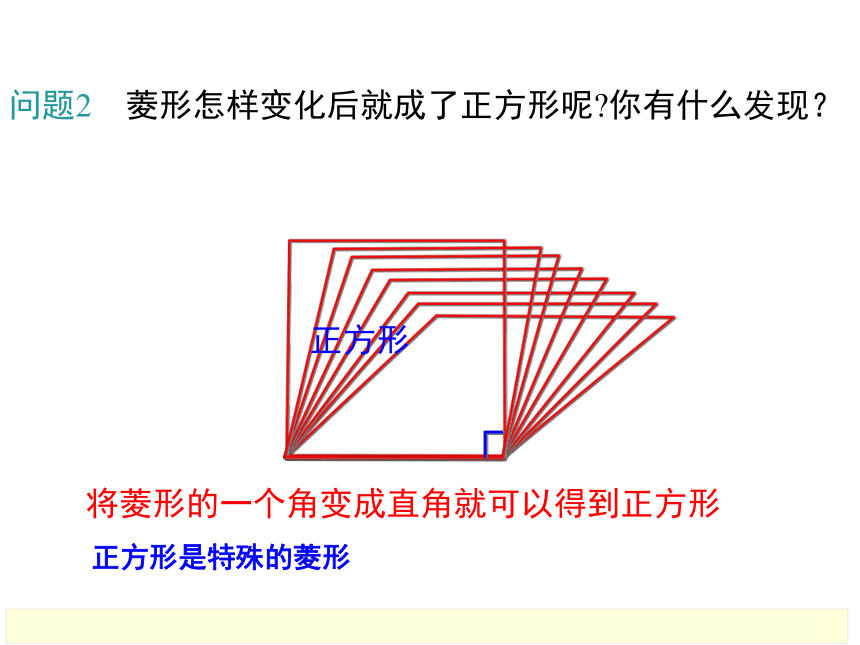
问题2 菱形怎样变化后就成了正方形呢?你有什么发现?
正方形
将菱形的一个角变成直角就可以得到正方形
正方形是特殊的菱形
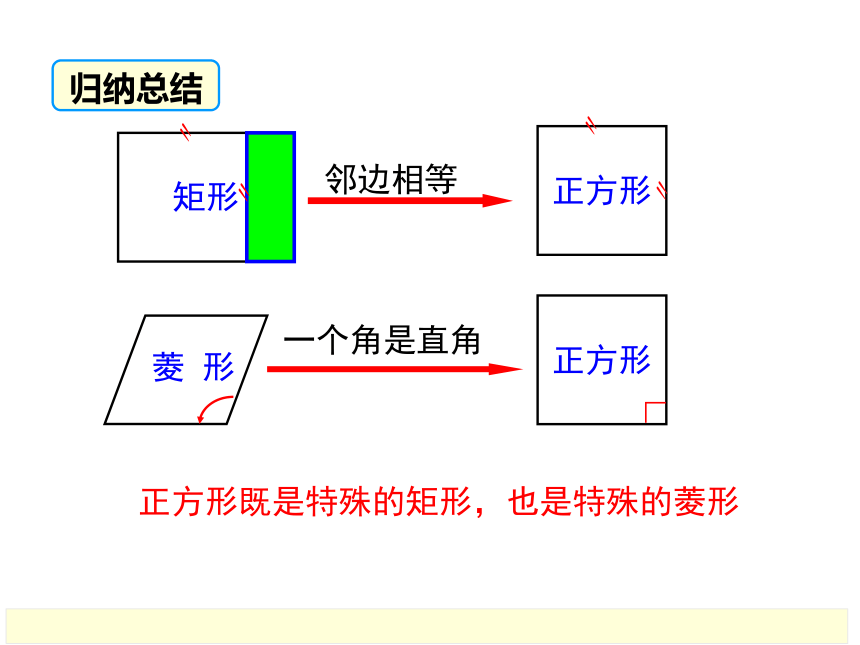
邻边相等
矩形
〃
〃
正方形
〃
〃
菱 形
一个角是直角
正方形
∟
正方形既是特殊的矩形,也是特殊的菱形
归纳总结
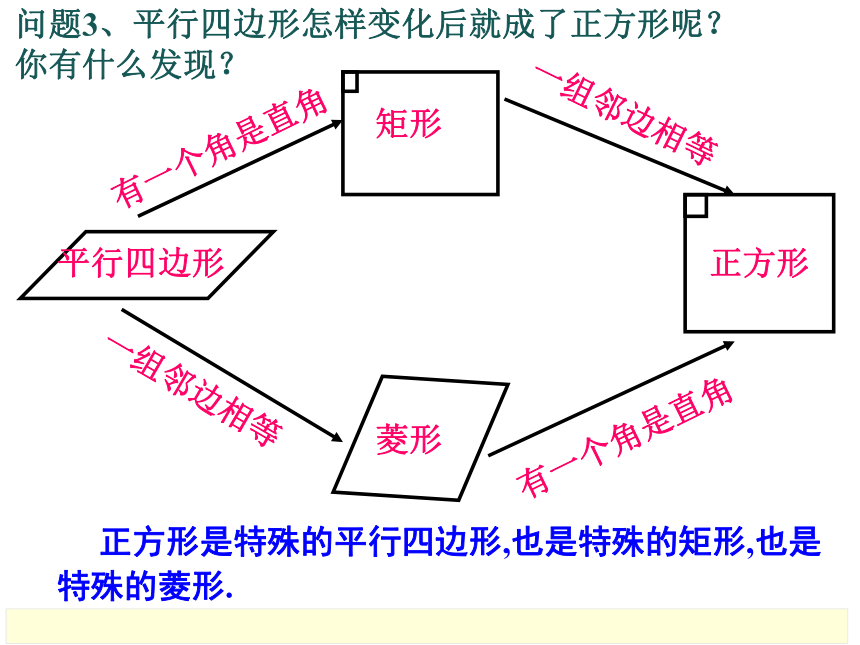
平行四边形
有一个角是直角
一组邻边相等
矩形
菱形
一组邻边相等
有一个角是直角
正方形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.
问题3、平行四边形怎样变化后就成了正方形呢?
你有什么发现?
新授
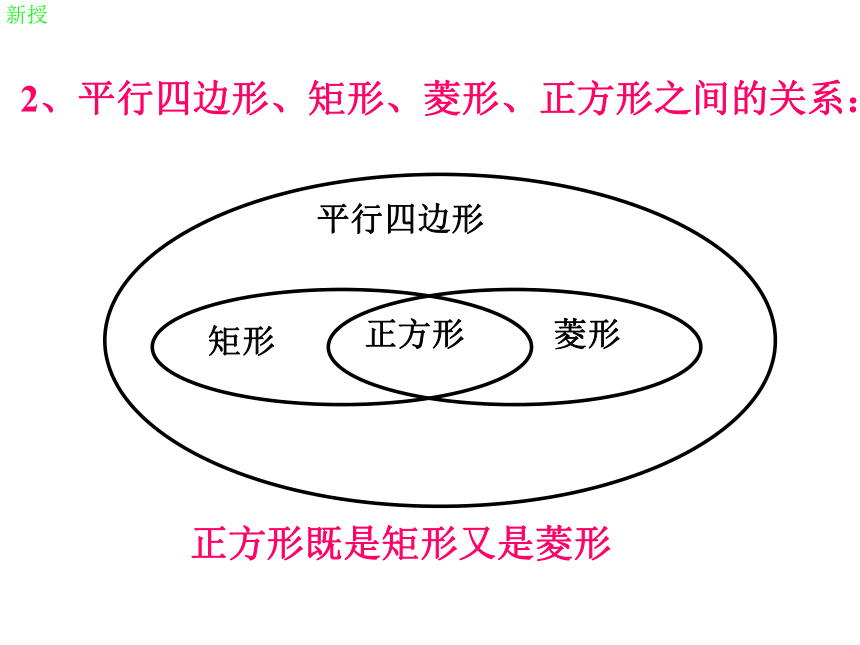
2、平行四边形、矩形、菱形、正方形之间的关系:
平行四边形
矩形
菱形
正方形
正方形既是矩形又是菱形
矩形
菱形
正
方
形
平行四边形
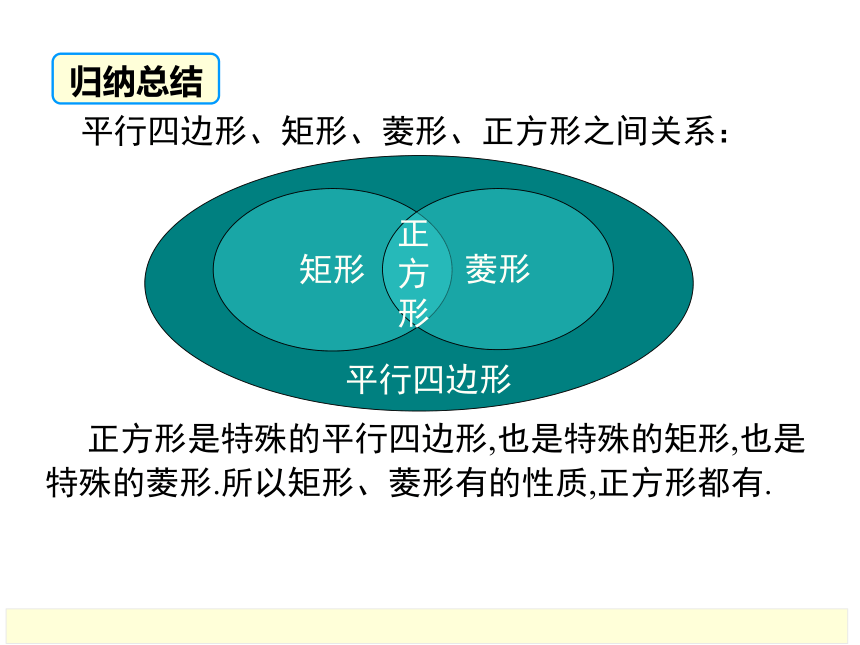
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
平行四边形、矩形、菱形、正方形之间关系:
归纳总结
3.正方形的性质
四条边相等,
四个角为直角
1.互相平分
3.每条对角线
平分一组对角
两条对称轴
两条对称轴
四条边相等,
对边平行
四个角为直角
四条对称轴
对边平行且相等
对角相等,
邻角互补
既中心对称图形,
也是轴对称图形
既中心对称图形,
也是轴对称图形
既中心对称图形,
也是轴对称图形
2.相等
1.互相平分
2.互相垂直
4.每条对角线
平分一组对角
1.互相平分
3.互相垂直
2.相等
矩形
菱形
正方形
边
角
对
角
线
对
称
性
对边平行
正方形性质
边
角
对角线
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
四条边都相等,
对边平行
四 个 角
都是直角
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
AC=BD,
4.每条对角线
平分一组对角
1.互相平分
3.互相垂直
2.相等
∴AB=BC=CD=AD
AB∥CD ,AD∥BC
∵四边形ABCD是正方形
∵四边形ABCD是正方形
∴OA=OB=OC=OD
AC⊥BD
∠OAB=∠OBA=∠OBC=∠OCB=∠OCD=∠ODC=∠OAD=∠ODA=45°
4、正方形的面积:
A
B
D
C
O
典型例题1: 如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.
解(1):
∵四边形ABCD是正方形
∴AD=BA,
∴∠BAQ+∠DAP=90°
∵DP⊥AQ
∴∠ADP+∠DAP=90°
∴∠BAQ=∠ADP
∵AQ⊥BE,DP⊥AQ
∴∠AQB=∠DPA=90°
∴△AQB≌△DPA(AAS)
∴AP=BQ
在△AQB和△DPA中
(2)①AQ﹣AP=PQ
②AQ﹣BQ=PQ
③DP﹣AP=PQ
④DP﹣BQ=PQ
∠BAD=90°
活学活用1:如图,已知正方形ABCD的边长为5,点E,F分别在AD,DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,则GH的长为多少?
解:∵四边形ABCD为正方形
∴AB=AD,∠BAE=∠D=90°
在△ABE和△DAF中
∴△ABE≌△DAF(SAS)
∴∠ABE=∠DAF
∵∠BAE=∠ABE+∠BEA=90°
∴∠DAF+∠BEA=90°
∴∠AGE=90°
∵点H为BF的中点
∵AE=DF=2
∴CF=CD﹣DF=5﹣2=3
在Rt△BCF中,由勾股定理得:
∴∠BGF=∠AGE=90°
∵四边形ABCD为正方形
∴BC=CD=5,∠C=90°
典型例题2:如图,正方形ABCD对角线交于点O,E为OA上任意一点,CF⊥BE于点F,交OB于点G.求证:(1)OE=OG;
(2)当E点在CA延长线上时,其他条件不变,结论还成立吗?请画出图形并证明
证明(1):
∵四边形ABCD是正方形
∴AC⊥BD,OB=OC
∴∠OCG+∠OGC=90°
∵CF⊥BE
∴∠FBG+∠FGB=90°
∵∠OGC=∠FGB
∴∠OCG=∠OBE
在△OGC和△OEB中
∴△OGC≌△OEB(ASA)
∴OE=OG
∴∠BOE=∠GOC=90°
典型例题2:如图,正方形ABCD对角线交于点O,E为OA上任意一点,CF⊥BE于点F,交OB于点G.求证:(1)OE=OG;
(2)当E点在CA延长线上时,其他条件不变,结论还成立吗?请画出图形并证明
证明(2):
成立,理由如下:
∴AC⊥BD,OB=OC
∴∠OBE+∠E=90°
∵CF⊥BE
∴∠FBG+∠G=90°
∵∠OBE=∠FBG
∴∠E=∠G
在△OGC和△OEB中
∴△OGC≌△OEB(AAS)
∴OE=OG
∵四边形ABCD是正方形
∴∠BOE=∠COG=90°
D
A
C
B
O
G
F
E
活学活用2:如图,在正方形ABCD中,O是对角线AC、BD的交点,过O点作OE⊥OF分别交AB、BC于点E、F,若AE=4,CF=3,则EF的长为多少?
解:
∵四边形ABCD是正方形
∴AO=BO,
∠OAE=∠OBF=45°
∴∠AOE+∠BOE=90°
∵OE⊥OF
∴∠BOF+∠BOE=90°
∴∠AOE=∠BOF
在△AOE和△BOF中
∴△AOE≌△BOF(ASA)
∴BF=AE=4
同理BE=CF=3
∵四边形ABCD是正方形
∠AOB=90°
∴∠ABC=90°
A
B
C
E
F
O
活学活用2:如图,在正方形ABCD中,O是对角线AC、BD的交点,过O点作OE⊥OF分别交AB、BC于点E、F,若AE=4,CF=3,则EF的长为多少?
我们还可以得出哪些结论呢?
G
H
P
G
H
P
A
B
C
E
F
O
课堂小结
谈一谈本节课
你的收获是什么?
邻边相等
矩形
〃
〃
正方形
〃
〃
菱 形
一个角是直角
正方形
∟
正方形定义:
有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
归纳总结
已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.
A
B
C
D
证明:∵四边形ABCD是正方形.
∴∠A=90°, AB=AC (正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
证一证
已知:如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证:AO=BO=CO=DO,AC⊥BD.
A
B
C
D
O
证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
思考 请同学们拿出准备好的正方形纸片,折一折,观察并思考.??正方形是不是轴对称图形?如果是,那么对称轴有几条?
对称性: .
对称轴: .
轴对称图形
4条
A
B
C
D
复习巩固
菱形的定义:
一组邻边相等的平行四边形叫做菱形
矩形的定义:
有一个角是直角的平行四边形叫做矩形。
第十八章 平行四边形
导入新课
讲授新课
当堂练习
课堂小结
学练优八年级数学下(RJ)
教学课件
第1课时 正方形的性质
导入新课
正方形是我们熟悉的几何图形,在生活中无处不在,观察下面图形中的正方形。
情景引入
讲授新课
矩 形
〃
〃
问题1:矩形怎样变化后就成了正方形呢?你有什么发现?
问题引入
正方形
1.正方形由矩形、菱形、平行四边形的演化过程.
将矩形的邻边变成相等的就可以得到正方形
正方形是特殊的矩形
问题2 菱形怎样变化后就成了正方形呢?你有什么发现?
正方形
将菱形的一个角变成直角就可以得到正方形
正方形是特殊的菱形
邻边相等
矩形
〃
〃
正方形
〃
〃
菱 形
一个角是直角
正方形
∟
正方形既是特殊的矩形,也是特殊的菱形
归纳总结
平行四边形
有一个角是直角
一组邻边相等
矩形
菱形
一组邻边相等
有一个角是直角
正方形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.
问题3、平行四边形怎样变化后就成了正方形呢?
你有什么发现?
新授
2、平行四边形、矩形、菱形、正方形之间的关系:
平行四边形
矩形
菱形
正方形
正方形既是矩形又是菱形
矩形
菱形
正
方
形
平行四边形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
平行四边形、矩形、菱形、正方形之间关系:
归纳总结
3.正方形的性质
四条边相等,
四个角为直角
1.互相平分
3.每条对角线
平分一组对角
两条对称轴
两条对称轴
四条边相等,
对边平行
四个角为直角
四条对称轴
对边平行且相等
对角相等,
邻角互补
既中心对称图形,
也是轴对称图形
既中心对称图形,
也是轴对称图形
既中心对称图形,
也是轴对称图形
2.相等
1.互相平分
2.互相垂直
4.每条对角线
平分一组对角
1.互相平分
3.互相垂直
2.相等
矩形
菱形
正方形
边
角
对
角
线
对
称
性
对边平行
正方形性质
边
角
对角线
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
四条边都相等,
对边平行
四 个 角
都是直角
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
AC=BD,
4.每条对角线
平分一组对角
1.互相平分
3.互相垂直
2.相等
∴AB=BC=CD=AD
AB∥CD ,AD∥BC
∵四边形ABCD是正方形
∵四边形ABCD是正方形
∴OA=OB=OC=OD
AC⊥BD
∠OAB=∠OBA=∠OBC=∠OCB=∠OCD=∠ODC=∠OAD=∠ODA=45°
4、正方形的面积:
A
B
D
C
O
典型例题1: 如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.
解(1):
∵四边形ABCD是正方形
∴AD=BA,
∴∠BAQ+∠DAP=90°
∵DP⊥AQ
∴∠ADP+∠DAP=90°
∴∠BAQ=∠ADP
∵AQ⊥BE,DP⊥AQ
∴∠AQB=∠DPA=90°
∴△AQB≌△DPA(AAS)
∴AP=BQ
在△AQB和△DPA中
(2)①AQ﹣AP=PQ
②AQ﹣BQ=PQ
③DP﹣AP=PQ
④DP﹣BQ=PQ
∠BAD=90°
活学活用1:如图,已知正方形ABCD的边长为5,点E,F分别在AD,DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,则GH的长为多少?
解:∵四边形ABCD为正方形
∴AB=AD,∠BAE=∠D=90°
在△ABE和△DAF中
∴△ABE≌△DAF(SAS)
∴∠ABE=∠DAF
∵∠BAE=∠ABE+∠BEA=90°
∴∠DAF+∠BEA=90°
∴∠AGE=90°
∵点H为BF的中点
∵AE=DF=2
∴CF=CD﹣DF=5﹣2=3
在Rt△BCF中,由勾股定理得:
∴∠BGF=∠AGE=90°
∵四边形ABCD为正方形
∴BC=CD=5,∠C=90°
典型例题2:如图,正方形ABCD对角线交于点O,E为OA上任意一点,CF⊥BE于点F,交OB于点G.求证:(1)OE=OG;
(2)当E点在CA延长线上时,其他条件不变,结论还成立吗?请画出图形并证明
证明(1):
∵四边形ABCD是正方形
∴AC⊥BD,OB=OC
∴∠OCG+∠OGC=90°
∵CF⊥BE
∴∠FBG+∠FGB=90°
∵∠OGC=∠FGB
∴∠OCG=∠OBE
在△OGC和△OEB中
∴△OGC≌△OEB(ASA)
∴OE=OG
∴∠BOE=∠GOC=90°
典型例题2:如图,正方形ABCD对角线交于点O,E为OA上任意一点,CF⊥BE于点F,交OB于点G.求证:(1)OE=OG;
(2)当E点在CA延长线上时,其他条件不变,结论还成立吗?请画出图形并证明
证明(2):
成立,理由如下:
∴AC⊥BD,OB=OC
∴∠OBE+∠E=90°
∵CF⊥BE
∴∠FBG+∠G=90°
∵∠OBE=∠FBG
∴∠E=∠G
在△OGC和△OEB中
∴△OGC≌△OEB(AAS)
∴OE=OG
∵四边形ABCD是正方形
∴∠BOE=∠COG=90°
D
A
C
B
O
G
F
E
活学活用2:如图,在正方形ABCD中,O是对角线AC、BD的交点,过O点作OE⊥OF分别交AB、BC于点E、F,若AE=4,CF=3,则EF的长为多少?
解:
∵四边形ABCD是正方形
∴AO=BO,
∠OAE=∠OBF=45°
∴∠AOE+∠BOE=90°
∵OE⊥OF
∴∠BOF+∠BOE=90°
∴∠AOE=∠BOF
在△AOE和△BOF中
∴△AOE≌△BOF(ASA)
∴BF=AE=4
同理BE=CF=3
∵四边形ABCD是正方形
∠AOB=90°
∴∠ABC=90°
A
B
C
E
F
O
活学活用2:如图,在正方形ABCD中,O是对角线AC、BD的交点,过O点作OE⊥OF分别交AB、BC于点E、F,若AE=4,CF=3,则EF的长为多少?
我们还可以得出哪些结论呢?
G
H
P
G
H
P
A
B
C
E
F
O
课堂小结
谈一谈本节课
你的收获是什么?
邻边相等
矩形
〃
〃
正方形
〃
〃
菱 形
一个角是直角
正方形
∟
正方形定义:
有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
归纳总结
已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.
A
B
C
D
证明:∵四边形ABCD是正方形.
∴∠A=90°, AB=AC (正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
证一证
已知:如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证:AO=BO=CO=DO,AC⊥BD.
A
B
C
D
O
证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
思考 请同学们拿出准备好的正方形纸片,折一折,观察并思考.??正方形是不是轴对称图形?如果是,那么对称轴有几条?
对称性: .
对称轴: .
轴对称图形
4条
A
B
C
D
复习巩固
菱形的定义:
一组邻边相等的平行四边形叫做菱形
矩形的定义:
有一个角是直角的平行四边形叫做矩形。
