18.1.1 平行四边形的性质课件(17张)
文档属性
| 名称 | 18.1.1 平行四边形的性质课件(17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 213.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 00:00:00 | ||
图片预览



文档简介
18.1平行四边形
八年级数学 第十八章 平行四边形
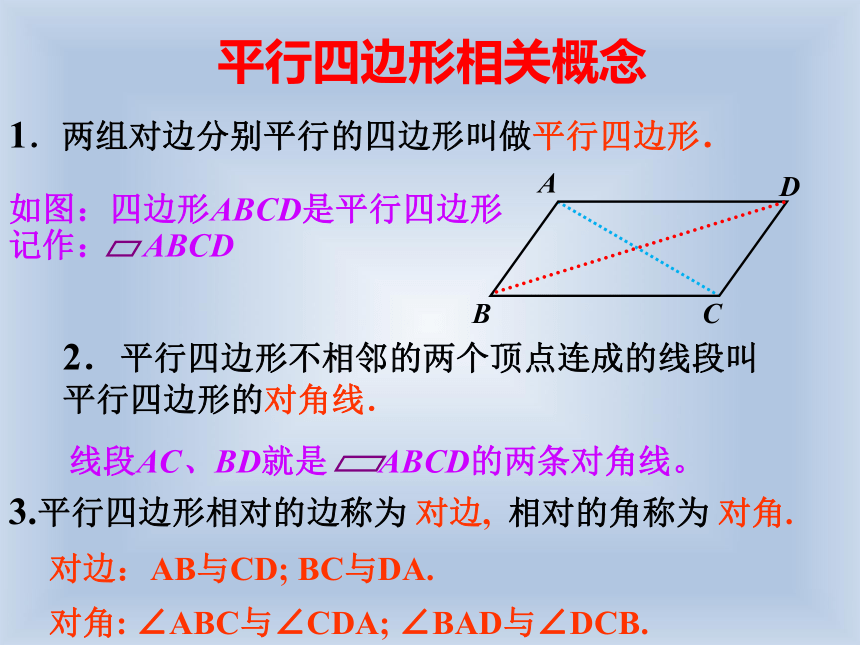
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形记作: ABCD
2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3.平行四边形相对的边称为 对边, 相对的角称为 对角.
平行四边形相关概念
A
D
C
B
线段AC、BD就是 ABCD的两条对角线。
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA; ∠BAD与∠DCB.
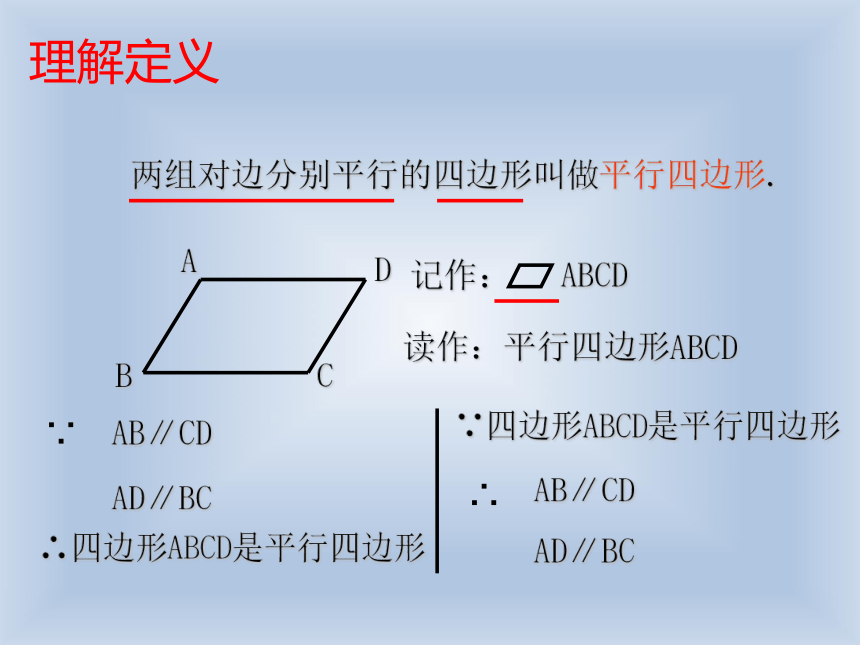
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
理解定义
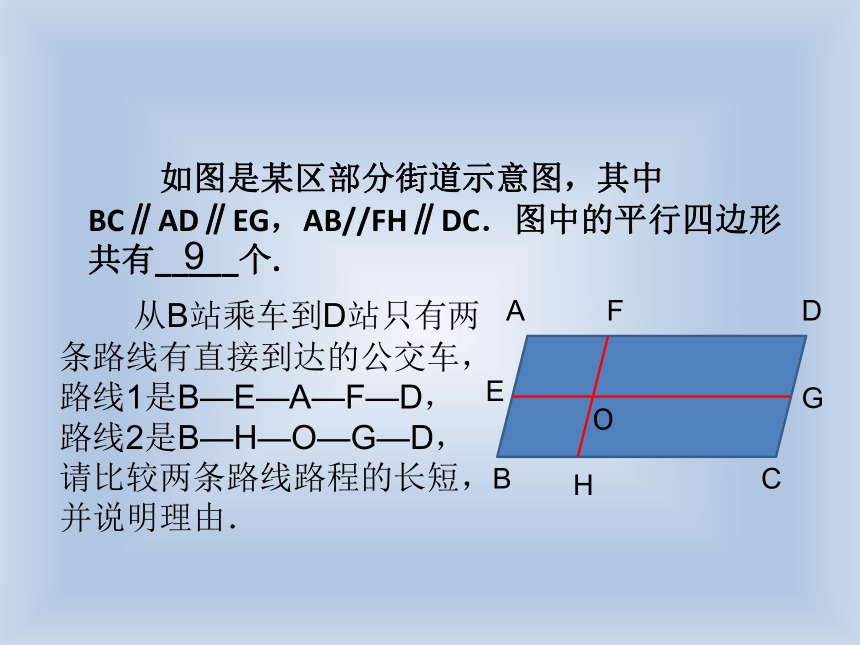
如图是某区部分街道示意图,其中BC∥AD∥EG,AB//FH∥DC.图中的平行四边形共有_____个.
9
从B站乘车到D站只有两
条路线有直接到达的公交车,
路线1是B—E—A—F—D,
路线2是B—H—O—G—D,
请比较两条路线路程的长短,
并说明理由.
A
B
C
D
E
G
F
H
O
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
拼一拼
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
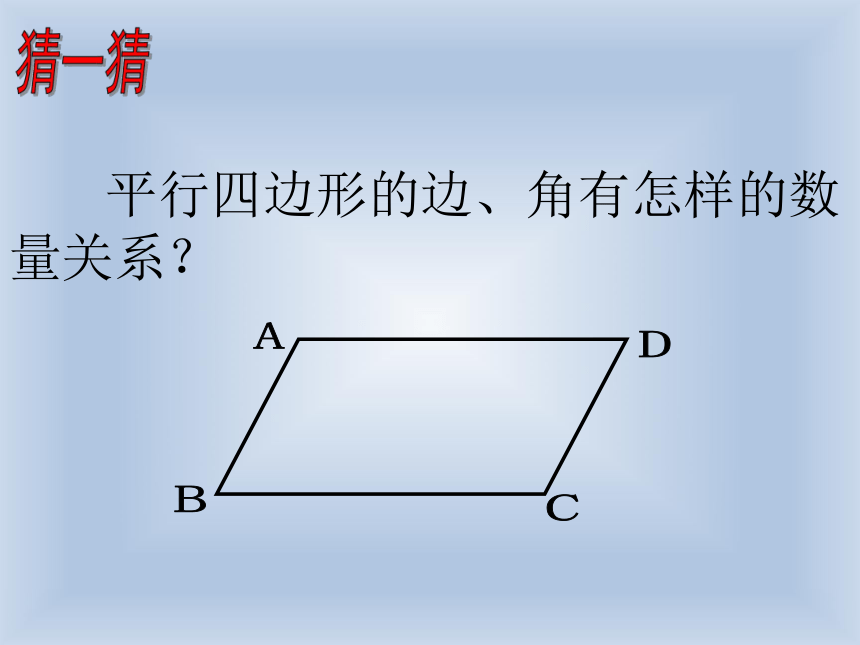
平行四边形的边、角有怎样的数量关系?
A
B
C
D
猜一猜
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确?
量一量
A
B
C
D
用你以前所学的知识证明猜想.
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
A
B
C
D
证一证
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
平行四边形的性质
几何语言:
定理1:平行四边形的两组对边分别相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
在 ABCD中,
AB=CD,AD=BC. (平行四边形的对边相等)
或
∠A= ∠C, ∠B= ∠D(平行四边形的对角相等)
∠A= ∠C, ∠B= ∠D(平行四边形的对角相等)
定理2:平行四边形的两组对角分别相等
1.如图:在 ABCD中,根据已知你能得到哪
些结论?为什么?
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
小试牛刀
如图 小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
解:∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m
知识应用
A
D
B
C
8cm
学以致用
1.如图, ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为( )
A 6cm B 12cm C 4cm D 8cm
A
B
D
C
A
D
B
C
2.如图,在 ABCD中,∠A:∠B=7:2,求∠C的度数.
E
A
B
D
C
9cm
5cm
1.如图,在 ABCD中,若BE平分∠ABC,则ED= .
4cm
2
3
5cm
5cm
4cm
1
好题大家练
2.如图,在平行四边形ABCD中,CE⊥AB,点E为垂足,如果∠A=125°,则∠BCE的度数为多少?
A
D
B
C
E
2、若 的周长是30㎝,AB :CB=3 :2,
则AD= ㎝,CD= ㎝.
ABCD
1、 的周长是20,已知AB=6,则BC=__,CD=__.
ABCD
4、
中,如果∠B的外角是 50°,那么平行四边形的每个内角是多少度?
ABCD
检测反馈
3 在 ∠A:∠B:∠C:∠D的值可能是( )A: 1:2:3:4 B: 1:2:2:1 C: 2:2:1:1 D: 1:2:1:2
ABCD中
5:如图,平行四边形ABCD中,点E、F在对角线BD上,且AE|| CF.
求证:AE=CF
A
B
C
D
E
F
通过本节课的学习,你有什么收获?
1.两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:对边平行
对边相等
对角相等
邻角互补
3.解决平行四边形的有关问题经常连结对角线转化为三角形。
课堂小结
八年级数学 第十八章 平行四边形
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形记作: ABCD
2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3.平行四边形相对的边称为 对边, 相对的角称为 对角.
平行四边形相关概念
A
D
C
B
线段AC、BD就是 ABCD的两条对角线。
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA; ∠BAD与∠DCB.
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
理解定义
如图是某区部分街道示意图,其中BC∥AD∥EG,AB//FH∥DC.图中的平行四边形共有_____个.
9
从B站乘车到D站只有两
条路线有直接到达的公交车,
路线1是B—E—A—F—D,
路线2是B—H—O—G—D,
请比较两条路线路程的长短,
并说明理由.
A
B
C
D
E
G
F
H
O
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
拼一拼
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
平行四边形的边、角有怎样的数量关系?
A
B
C
D
猜一猜
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确?
量一量
A
B
C
D
用你以前所学的知识证明猜想.
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
A
B
C
D
证一证
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
平行四边形的性质
几何语言:
定理1:平行四边形的两组对边分别相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
在 ABCD中,
AB=CD,AD=BC. (平行四边形的对边相等)
或
∠A= ∠C, ∠B= ∠D(平行四边形的对角相等)
∠A= ∠C, ∠B= ∠D(平行四边形的对角相等)
定理2:平行四边形的两组对角分别相等
1.如图:在 ABCD中,根据已知你能得到哪
些结论?为什么?
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
小试牛刀
如图 小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
解:∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m
知识应用
A
D
B
C
8cm
学以致用
1.如图, ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为( )
A 6cm B 12cm C 4cm D 8cm
A
B
D
C
A
D
B
C
2.如图,在 ABCD中,∠A:∠B=7:2,求∠C的度数.
E
A
B
D
C
9cm
5cm
1.如图,在 ABCD中,若BE平分∠ABC,则ED= .
4cm
2
3
5cm
5cm
4cm
1
好题大家练
2.如图,在平行四边形ABCD中,CE⊥AB,点E为垂足,如果∠A=125°,则∠BCE的度数为多少?
A
D
B
C
E
2、若 的周长是30㎝,AB :CB=3 :2,
则AD= ㎝,CD= ㎝.
ABCD
1、 的周长是20,已知AB=6,则BC=__,CD=__.
ABCD
4、
中,如果∠B的外角是 50°,那么平行四边形的每个内角是多少度?
ABCD
检测反馈
3 在 ∠A:∠B:∠C:∠D的值可能是( )A: 1:2:3:4 B: 1:2:2:1 C: 2:2:1:1 D: 1:2:1:2
ABCD中
5:如图,平行四边形ABCD中,点E、F在对角线BD上,且AE|| CF.
求证:AE=CF
A
B
C
D
E
F
通过本节课的学习,你有什么收获?
1.两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:对边平行
对边相等
对角相等
邻角互补
3.解决平行四边形的有关问题经常连结对角线转化为三角形。
课堂小结
