6.4.3 第3课时 余弦定理、正弦定理应用举例课件(共23张PPT)
文档属性
| 名称 | 6.4.3 第3课时 余弦定理、正弦定理应用举例课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 08:49:10 | ||
图片预览






文档简介
第3课时 余弦定理、正弦定理应用举例
第六章 6.4.3 余弦定理、正弦定理
高中数学人教A版(2019)必修第二册
1.会用正弦定理、余弦定理解决生产实践中有关距离、高度、角度的测量问题.
2.培养提出问题、正确分析问题、独立解决问题的能力.
学习目标
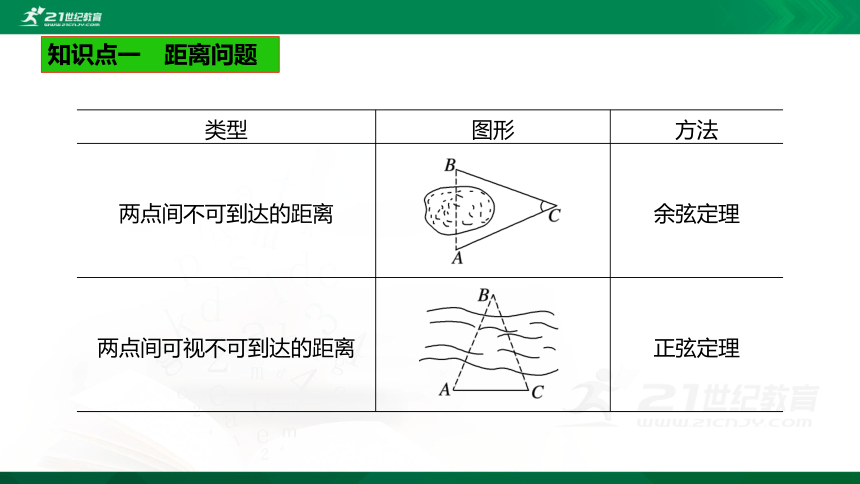
知识点一 距离问题
类型
图形
方法
两点间不可到达的距离
?
余弦定理
两点间可视不可到达的距离
?
正弦定理
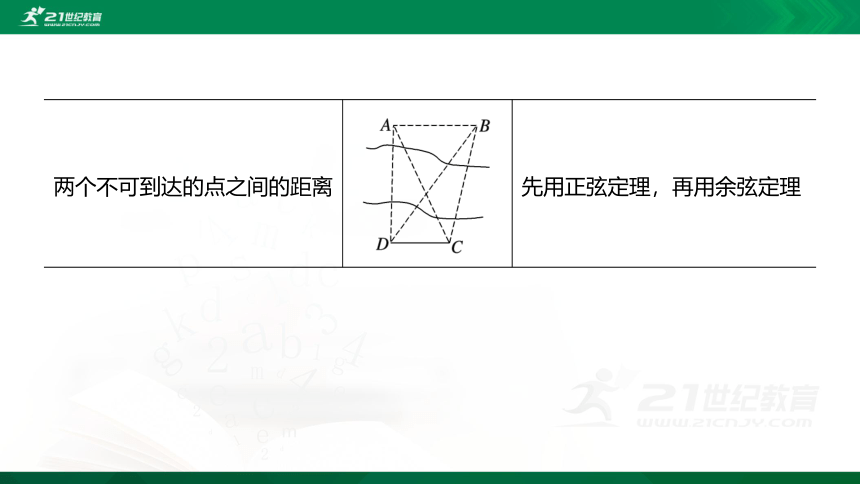
两个不可到达的点之间的距离
先用正弦定理,再用余弦定理
知识点二 高度问题
类型
简图
计算方法
底部可达
?
测得BC=a,∠BCA=C,AB=a·tan C.
底部
不可达
点B与C,D共线
?
测得CD=a及C与∠ADB的度数.
先由正弦定理求出AC或AD,再解三角形得AB的值.
点B与C,D不共线
?
测得CD=a及∠BCD,∠BDC,∠ACB的度数.
在△BCD中由正弦定理求得BC,再解三角形得AB的值.
知识点三 角度问题
测量角度问题主要是指在海上或空中测量角度的问题,如确定目标的方位,观察某一建筑物的视角等.解决它们的关键是根据题意和图形及有关概念,确定所求的角在哪个三角形中,该三角形中已知哪些量,需要求哪些量.通常是根据题意,从实际问题中抽象出一个或几个三角形,然后通过解这些三角形得到所求的量,从而得到实际问题的解.
思考辨析 判断正误
1.仰角是视线与视线在水平面的射影的夹角.( )
2.两点间不可通又不可视问题的测量方案实质是构造已知两边及夹角的三角形并求解.( )
3.两点间可视但不可到达问题的测量方案实质是构造已知两角及一边的三角形并求解.( )
4.高度问题大多通过正(余)弦定理构造直角三角形来解决.( )
√
√
√
√
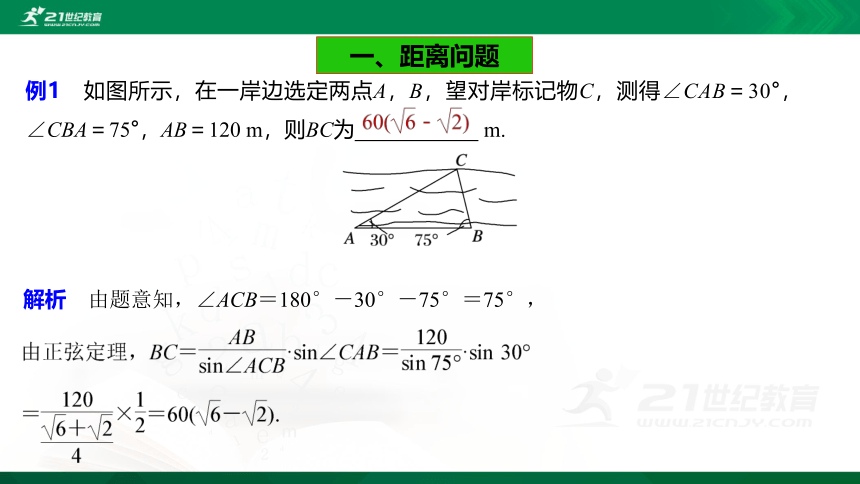
例1 如图所示,在一岸边选定两点A,B,望对岸标记物C,测得∠CAB=30°,∠CBA=75°,AB=120 m,则BC为 m.
一、距离问题
解析 由题意知,∠ACB=180°-30°-75°=75°,
反思感悟
求不可达的两点间的距离时,由于构造的三角形的两边均不可直接测量,故只能寻求构造已知两角及一边的三角形.
跟踪训练1 A,B两地之间隔着一个山岗,如图,现选择另一点C,测得CA=7 km,CB=5 km,C=60°,则A,B两点之间的距离为 km.
解析 由余弦定理,
得AB2=CA2+CB2-2CA·CB·cos C
二、高度问题
例2 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10 m到位置D,测得∠BDC=45°,则塔AB的高是
√
解析 在△BCD中,CD=10 m,∠BDC=45°,
∠BCD=15°+90°=105°,∠DBC=30°,
反思感悟
此类问题特点:底部不可到达,且涉及与地面垂直的平面,观测者两次观测点所在直线不经过“目标物”,解决办法是把目标高度转化为地平面内某量,从而把空间问题转化为平面内解三角形问题.
跟踪训练2 某登山队在山脚A处测得山顶B的仰角为35°,沿倾斜角为20°的斜坡前进1 000 m后到达D处,又测得山顶的仰角为65°,则山的高度为 m.(精确到1 m)
811
解析 如图,过点D作DE∥AC交BC于点E,
因为∠DAC=20°,所以∠ADE=160°,
于是∠ADB=360°-160°-65°=135°.
又∠BAD=35°-20°=15°,所以∠ABD=30°.
在△ABD中,由正弦定理,
在Rt△ABC中,BC=ABsin 35°≈811(m).
所以山的高度为811 m.
三、角度问题
例3 甲船在A点发现乙船在北偏东60°的B处,乙船以每小时a海里的速度向北行驶,已知甲船的速度是每小时 a海里,问甲船应沿着什么方向前进,才能最快与乙船相遇?
解 如图所示.设经过t小时两船在C点相遇,
则在△ABC中,BC=at海里,
B=90°+30°=120°,
∵0°<∠CAB<60°,∴∠CAB=30°,∴∠DAC=60°-30°=30°,
∴甲船应沿着北偏东30°的方向前进,才能最快与乙船相遇.
跟踪训练3 当太阳光与水平面的倾斜角为60°时,一根长为2 m的竹竿如图所示放置,要使它的影子最长,则竹竿与地面所成的角是
A.15° B.30°
C.45° D.60°
√
解析 设竹竿与地面所成的角为α,影子长为x m.
∵30°<120°-α<120°,
∴当120°-α=90°,即α=30°时,x有最大值.
即当竹竿与地面所成的角是30°时,影子最长.
1.如图所示,设A,B两点在河的两岸,一测量者与A在河的同侧,在所在的河岸边先确定一点C,测出A,C的距离为50 m,∠ACB=45°,∠CAB=105°后,可以计算出A,B两点的距离为
√
解析 ∠ABC=180°-45°-105°=30°,在△ABC中,
1
2
3
4
5
课堂练习
2.如图,要测出山上一座天文台BC的高,从山腰A处测得AC=60 m,天文台最高处B的仰角为45°,天文台底部C的仰角为15°,则天文台BC的高为
√
解析 由题图,可得∠B=45°,∠BAC=30°,
1
2
3
4
5
1
2
3
4
5
3.如图,在河岸AC测量河的宽度,测量下列四组数据,较适宜的是
A.a,c,α B.b,c,α
C.c,a,β D.b,α,γ
√
4.甲骑电动车以24 km/h的速度沿着正北方向的公路行驶,在点A处望见电视塔S在电动车的北偏东30°方向上,15 min后到点B处望见电视塔在电动车的北偏东75°方向上,则电动车在点B时与电视塔S的距离是
1
2
3
4
5
√
5.如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100 m到达B处,又测得C对于山坡的斜度为45°,若CD=50 m,山坡对于地平面的坡度为θ,则cos θ等于
√
1
2
3
4
5
1.知识清单:不可到达的距离、高度、角度等实际问题的测量方案.
2.方法归纳:数形结合.
3.常见误区:方位角是易错点.
课堂小结
谢谢聆听
第六章 6.4.3 余弦定理、正弦定理
高中数学人教A版(2019)必修第二册
1.会用正弦定理、余弦定理解决生产实践中有关距离、高度、角度的测量问题.
2.培养提出问题、正确分析问题、独立解决问题的能力.
学习目标
知识点一 距离问题
类型
图形
方法
两点间不可到达的距离
?
余弦定理
两点间可视不可到达的距离
?
正弦定理
两个不可到达的点之间的距离
先用正弦定理,再用余弦定理
知识点二 高度问题
类型
简图
计算方法
底部可达
?
测得BC=a,∠BCA=C,AB=a·tan C.
底部
不可达
点B与C,D共线
?
测得CD=a及C与∠ADB的度数.
先由正弦定理求出AC或AD,再解三角形得AB的值.
点B与C,D不共线
?
测得CD=a及∠BCD,∠BDC,∠ACB的度数.
在△BCD中由正弦定理求得BC,再解三角形得AB的值.
知识点三 角度问题
测量角度问题主要是指在海上或空中测量角度的问题,如确定目标的方位,观察某一建筑物的视角等.解决它们的关键是根据题意和图形及有关概念,确定所求的角在哪个三角形中,该三角形中已知哪些量,需要求哪些量.通常是根据题意,从实际问题中抽象出一个或几个三角形,然后通过解这些三角形得到所求的量,从而得到实际问题的解.
思考辨析 判断正误
1.仰角是视线与视线在水平面的射影的夹角.( )
2.两点间不可通又不可视问题的测量方案实质是构造已知两边及夹角的三角形并求解.( )
3.两点间可视但不可到达问题的测量方案实质是构造已知两角及一边的三角形并求解.( )
4.高度问题大多通过正(余)弦定理构造直角三角形来解决.( )
√
√
√
√
例1 如图所示,在一岸边选定两点A,B,望对岸标记物C,测得∠CAB=30°,∠CBA=75°,AB=120 m,则BC为 m.
一、距离问题
解析 由题意知,∠ACB=180°-30°-75°=75°,
反思感悟
求不可达的两点间的距离时,由于构造的三角形的两边均不可直接测量,故只能寻求构造已知两角及一边的三角形.
跟踪训练1 A,B两地之间隔着一个山岗,如图,现选择另一点C,测得CA=7 km,CB=5 km,C=60°,则A,B两点之间的距离为 km.
解析 由余弦定理,
得AB2=CA2+CB2-2CA·CB·cos C
二、高度问题
例2 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10 m到位置D,测得∠BDC=45°,则塔AB的高是
√
解析 在△BCD中,CD=10 m,∠BDC=45°,
∠BCD=15°+90°=105°,∠DBC=30°,
反思感悟
此类问题特点:底部不可到达,且涉及与地面垂直的平面,观测者两次观测点所在直线不经过“目标物”,解决办法是把目标高度转化为地平面内某量,从而把空间问题转化为平面内解三角形问题.
跟踪训练2 某登山队在山脚A处测得山顶B的仰角为35°,沿倾斜角为20°的斜坡前进1 000 m后到达D处,又测得山顶的仰角为65°,则山的高度为 m.(精确到1 m)
811
解析 如图,过点D作DE∥AC交BC于点E,
因为∠DAC=20°,所以∠ADE=160°,
于是∠ADB=360°-160°-65°=135°.
又∠BAD=35°-20°=15°,所以∠ABD=30°.
在△ABD中,由正弦定理,
在Rt△ABC中,BC=ABsin 35°≈811(m).
所以山的高度为811 m.
三、角度问题
例3 甲船在A点发现乙船在北偏东60°的B处,乙船以每小时a海里的速度向北行驶,已知甲船的速度是每小时 a海里,问甲船应沿着什么方向前进,才能最快与乙船相遇?
解 如图所示.设经过t小时两船在C点相遇,
则在△ABC中,BC=at海里,
B=90°+30°=120°,
∵0°<∠CAB<60°,∴∠CAB=30°,∴∠DAC=60°-30°=30°,
∴甲船应沿着北偏东30°的方向前进,才能最快与乙船相遇.
跟踪训练3 当太阳光与水平面的倾斜角为60°时,一根长为2 m的竹竿如图所示放置,要使它的影子最长,则竹竿与地面所成的角是
A.15° B.30°
C.45° D.60°
√
解析 设竹竿与地面所成的角为α,影子长为x m.
∵30°<120°-α<120°,
∴当120°-α=90°,即α=30°时,x有最大值.
即当竹竿与地面所成的角是30°时,影子最长.
1.如图所示,设A,B两点在河的两岸,一测量者与A在河的同侧,在所在的河岸边先确定一点C,测出A,C的距离为50 m,∠ACB=45°,∠CAB=105°后,可以计算出A,B两点的距离为
√
解析 ∠ABC=180°-45°-105°=30°,在△ABC中,
1
2
3
4
5
课堂练习
2.如图,要测出山上一座天文台BC的高,从山腰A处测得AC=60 m,天文台最高处B的仰角为45°,天文台底部C的仰角为15°,则天文台BC的高为
√
解析 由题图,可得∠B=45°,∠BAC=30°,
1
2
3
4
5
1
2
3
4
5
3.如图,在河岸AC测量河的宽度,测量下列四组数据,较适宜的是
A.a,c,α B.b,c,α
C.c,a,β D.b,α,γ
√
4.甲骑电动车以24 km/h的速度沿着正北方向的公路行驶,在点A处望见电视塔S在电动车的北偏东30°方向上,15 min后到点B处望见电视塔在电动车的北偏东75°方向上,则电动车在点B时与电视塔S的距离是
1
2
3
4
5
√
5.如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100 m到达B处,又测得C对于山坡的斜度为45°,若CD=50 m,山坡对于地平面的坡度为θ,则cos θ等于
√
1
2
3
4
5
1.知识清单:不可到达的距离、高度、角度等实际问题的测量方案.
2.方法归纳:数形结合.
3.常见误区:方位角是易错点.
课堂小结
谢谢聆听
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
