2020-2021学年九年级下册数学苏科新版《第6章 图形的相似》单元测试题(word版含解析)
文档属性
| 名称 | 2020-2021学年九年级下册数学苏科新版《第6章 图形的相似》单元测试题(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 422.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 21:40:19 | ||
图片预览


文档简介
2020-2021学年九年级下册数学苏科新版《第6章
图形的相似》单元测试题
一.选择题
1.已知mn=ef,则下列式子错误的是( )
A.
B.
C.
D.
2.小明的数学作业本的纸上都是等距离的横线,他在上面任意画一条不与这些横线平行的直线,那么这条直线被这些横线所截得的线段( )
A.平行
B.相等
C.平行或相等
D.不相等
3.在相同水压下,口径为4cm的水管的出水量是口径为1cm的水管出水量的( )
A.4倍
B.8倍
C.12倍
D.16倍
4.已知:△ABC∽△DEF相似,,那么△ABC和△DEF的相似比是( )
A.
B.
C.
D.
5.如图,∠CAB=∠CBD,AB=4,AC=6,BD=7.5,BC=5,则CD的长为( )
A.
B.1
C.3.5
D.6
6.在某一时刻测得1米高的竹竿的影长为0.9米,同时测得一棵树的影长,落在地面上的影长为1.8米,落在墙上的影长为0.4米,则这棵树的高度为( )
A.2米
B.2.4米
C.2.2米
D.2.8米
7.若x、y为非零线段的长,则下列说法错误的是( )
A.若=,则=
B.若=,则=
C.若=,则=
D.若2x﹣5y=0,则=
8.如图,在△ABC中,AB=AC=8,∠A=36°,BD平分∠ABC交AC于点D,则AD=( )
A.4
B.4﹣4
C.﹣4+4
D.4﹣4或﹣4+4
9.如图,∠AOD=90°,OA=OB=BC=CD,那么下列结论成立的是( )
A.△OAB∽△OCA
B.△OAB∽△ODA
C.△BAC∽△BDA
D.以上结论都不成立
10.如果一个图形上各点的横坐标保持不变,而纵坐标分别都变化为原来的,那么所得的图形与原图形相比( )
A.形状不变,图形缩小为原来的一半
B.形状不变,图形放大为原来的2倍
C.整个图形被横向压缩为原来的一半
D.整个图形被纵向压缩为原来的一半
二.填空题
11.某人背对路灯离路灯1m处时,影长为2m,他再往前走2m时,影长为
m.
12.在Rt△ABC中,AD是斜边上的高,若AB=,DC=2,则BD=
,AC=
.
13.如图,添上条件
,则△ABC∽△ADE.
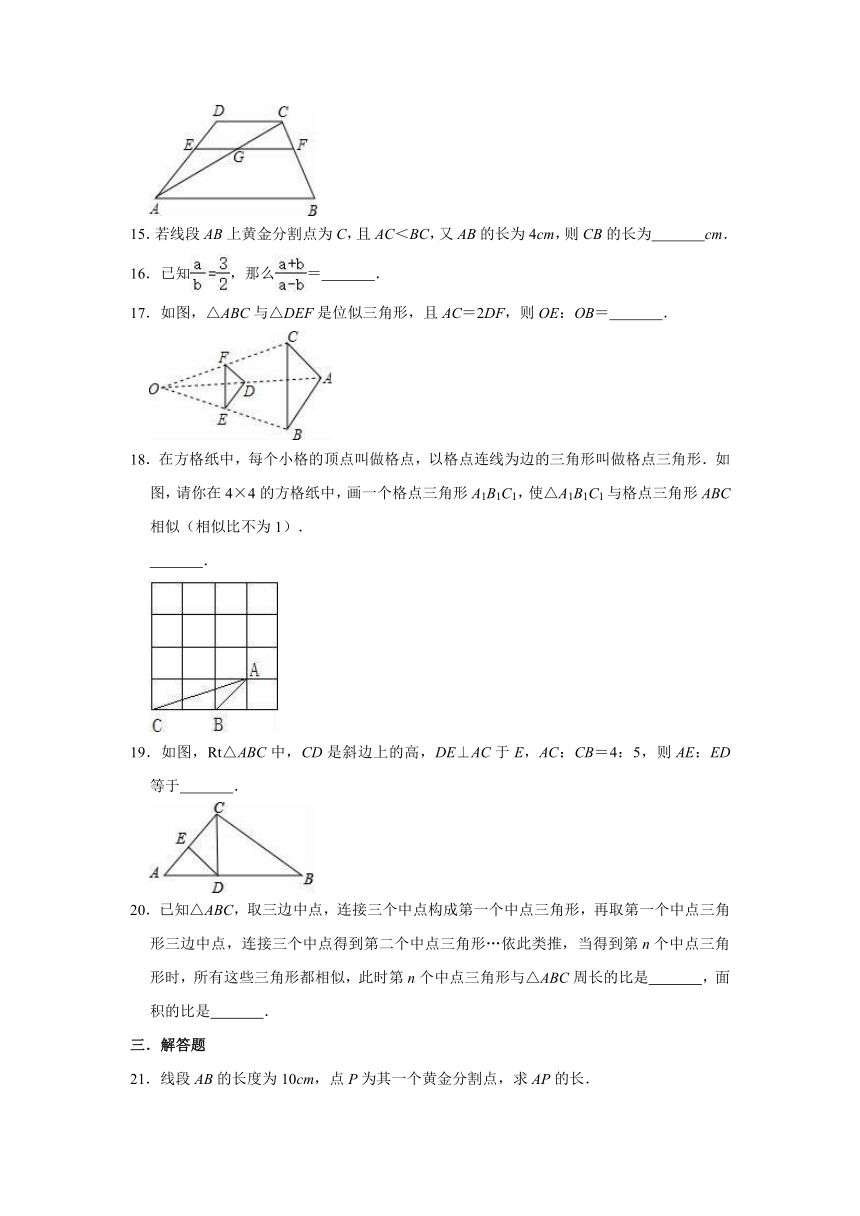
14.如图,梯形ABCD中,DC∥EF∥AB,AC交EF于G.若AE=2ED,CF=2cm,AG=5cm,则BC=
cm,CG=
cm.
15.若线段AB上黄金分割点为C,且AC<BC,又AB的长为4cm,则CB的长为
cm.
16.已知,那么=
.
17.如图,△ABC与△DEF是位似三角形,且AC=2DF,则OE:OB=
.
18.在方格纸中,每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.如图,请你在4×4的方格纸中,画一个格点三角形A1B1C1,使△A1B1C1与格点三角形ABC相似(相似比不为1).
.
19.如图,Rt△ABC中,CD是斜边上的高,DE⊥AC于E,AC:CB=4:5,则AE:ED等于
.
20.已知△ABC,取三边中点,连接三个中点构成第一个中点三角形,再取第一个中点三角形三边中点,连接三个中点得到第二个中点三角形…依此类推,当得到第n个中点三角形时,所有这些三角形都相似,此时第n个中点三角形与△ABC周长的比是
,面积的比是
.
三.解答题
21.线段AB的长度为10cm,点P为其一个黄金分割点,求AP的长.
22.已知==,求的值.
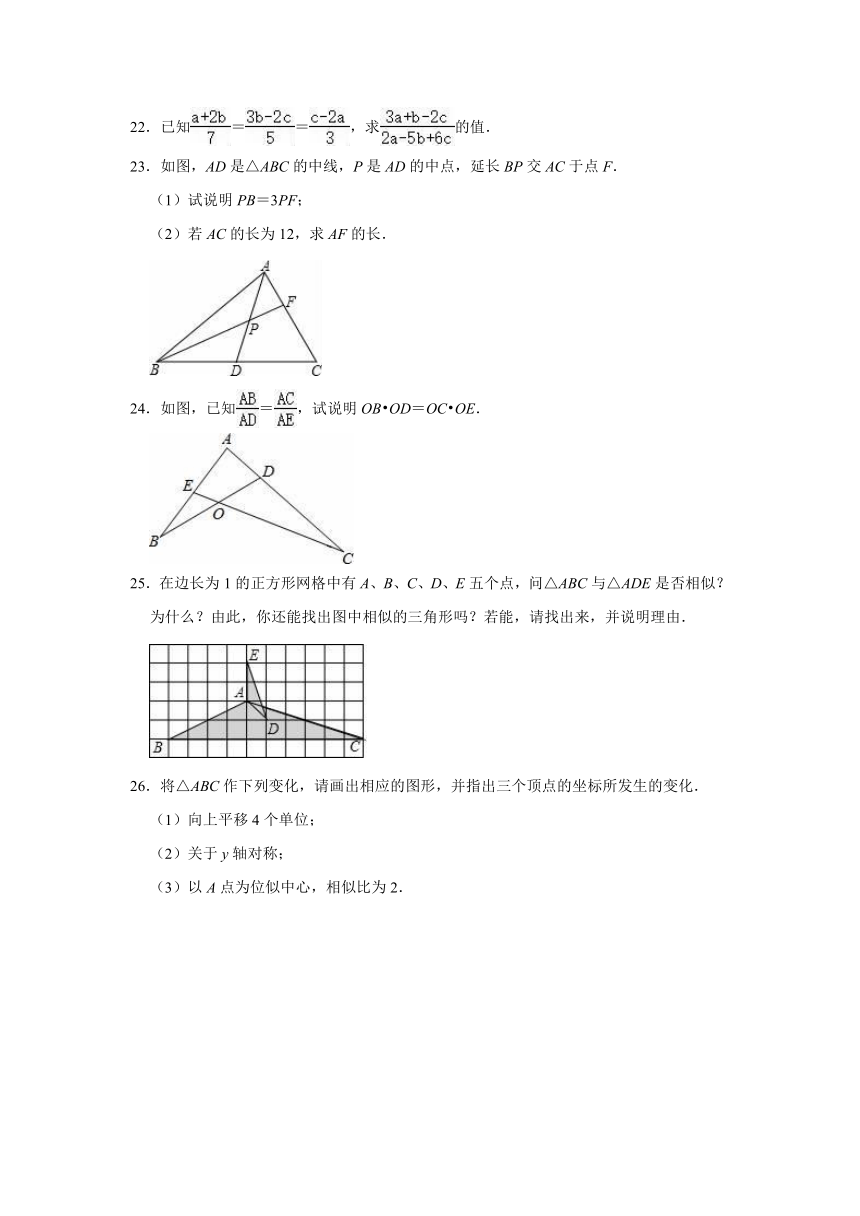
23.如图,AD是△ABC的中线,P是AD的中点,延长BP交AC于点F.
(1)试说明PB=3PF;
(2)若AC的长为12,求AF的长.
24.如图,已知=,试说明OB?OD=OC?OE.
25.在边长为1的正方形网格中有A、B、C、D、E五个点,问△ABC与△ADE是否相似?为什么?由此,你还能找出图中相似的三角形吗?若能,请找出来,并说明理由.
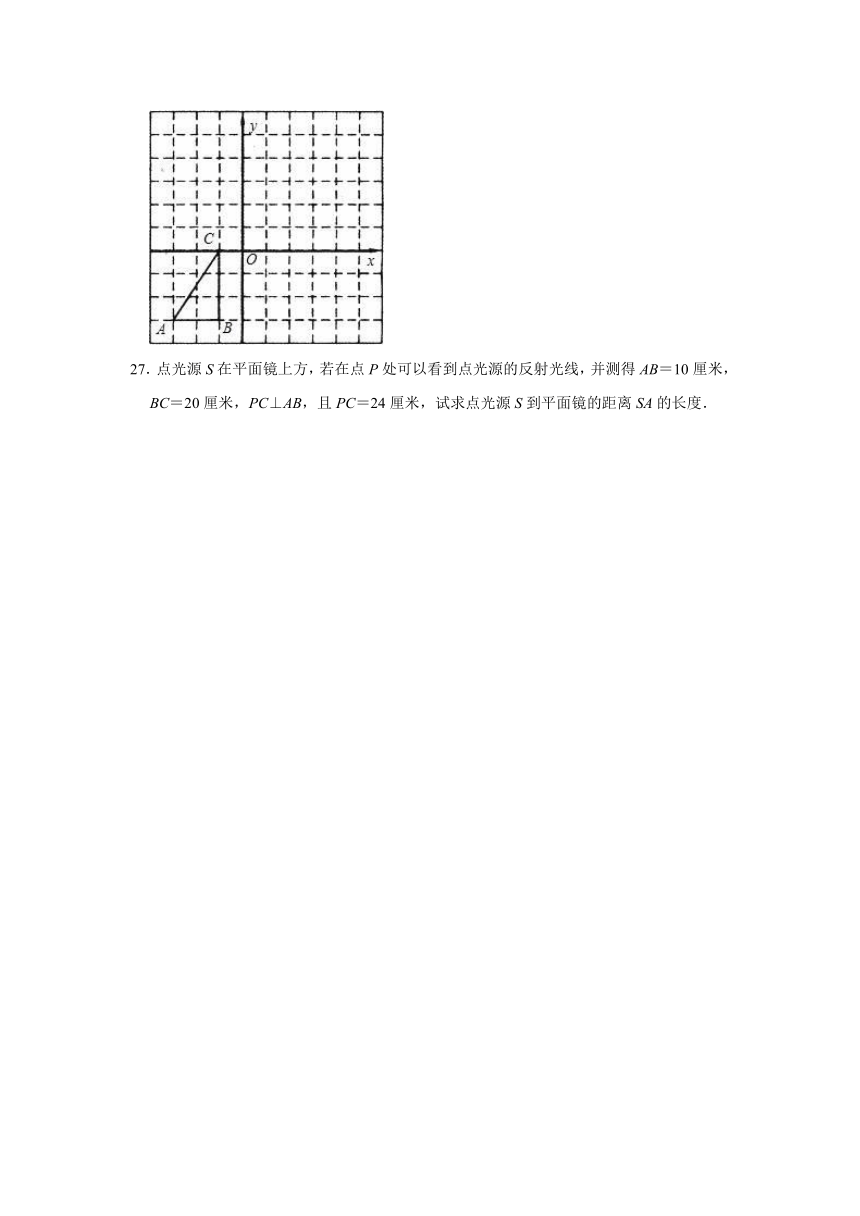
26.将△ABC作下列变化,请画出相应的图形,并指出三个顶点的坐标所发生的变化.
(1)向上平移4个单位;
(2)关于y轴对称;
(3)以A点为位似中心,相似比为2.
27.点光源S在平面镜上方,若在点P处可以看到点光源的反射光线,并测得AB=10厘米,BC=20厘米,PC⊥AB,且PC=24厘米,试求点光源S到平面镜的距离SA的长度.
参考答案与试题解析
一.选择题
1.解:根据比例的基本性质,
所给选项中,只有B项经转换后为等积式是me=nf,和已知不符,错误.
故选:B.
2.解:根据平行线等分线段定理,得这条直线被横线所截得的线段相等.故选B.
3.解:水管的截面是圆,两个圆是相似图形,它们的口径分别是4cm和1cm,得到相似比为4:1,所以面积的比是16:1.
所以出水量的比为16:1.
故选:D.
4.解:因为△ABC∽△DEF相似,且,
所以△ABC和△DEF的相似比,故选A.
5.解:∵AB=4,AC=6,BD=7.5,BC=5,
∴=,
∵∠CAB=∠CBD,
∴△ABC∽△BCD,
∴=,
∴CD=BC=×5=.
故选:A.
6.解:设影长为1.8m时树的高度为hm,
∵在某一时刻测得直立的标杆长0.9m,其影长为1m,
∴,
解得x=2m,
∴树的高度=2+0.4=2.4m,
答:树的高度是2.4米.
故选:B.
7.解:A、若=,则=,故此选项正确;
B、若=,则=,∴=,=,∴=,故此选项正确;
C、若=,则=,∴=,故此选项正确;
D、若2x﹣5y=0,则x=y,∴==,故此选项错误;
故选:D.
8.解:∵AB=AC=8,
∴∠ABC=∠C=(180°﹣∠A)=(180°﹣36°)=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=∠ABC=36°,
∴∠A=∠ABD,
∴AD=BD,
∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴AD=BD=BC,
∴∠A=∠CBD,∠C=∠C,
∴△ABC∽△BCD,
∴AC:BC=BC:CD,
∴AC:AD=AD:CD,
∴点D为AC的黄金分割点,
∴AD=AC=×8=4()=4.
故选:B.
9.解:∵∠AOD=90°,设OA=OB=BC=CD=x
∴AB=x,AC=x,AD=x,OC=2x,OD=3x,BD=2x
∴,,
∴
∴△BAC∽△BDA
故选:C.
10.解:∵一个图形上各点的横坐标保持不变,而纵坐标分别都变化为原来的,
∴整个图形被纵向压缩为原来的一半
故选:D.
二.填空题
11.解:∵人身高:路灯高=影长:影长与到路灯距离之和,设再走2m时,影长为x
∴人身高:路灯高=2:(2+1)=x:(x+2+1)
解得影长x=6(m)
故他再往前走2m时,影长为6m.
12.解:根据射影定理可得:AB2=BD×BC;AC2=CD×BC,
∴解得:BD=1,AC=.
故答案为:1,.
13.解:∵∠A=∠A
∴当BC∥DE或∠ABC=∠ADE或时,△ABC∽△ADE.
14.解:∵DC∥EF∥AB,
∴==2,又AG=5cm,
∴GC=2.5cm.
=,CF=2cm,
∴BC=6cm.
故答案为:6,2.5.
15.解:根据黄金分割点的概念得:CB=AB=2﹣2.
故本题答案为:2﹣2.
16.解:∵=,
∴设a=3k,b=2k,
则==5.
故答案为:5.
17.解:∵△ABC与△DEF是位似三角形,
∴DF∥AC,EF∥BC
∴△OAC∽△ODF,OE:OB=OF:OC
∴OF:OC=DF:AC
∵AC=2DF
∴OE:OB=DF:AC=1:2.
故答案为:1:2.
18.解:如图所示:
19.解:在Rt△ACB中,
∵∠A+∠B=90°,∠A+∠ACD=90°,∠B+∠BCD=90°
∴∠A=∠DCB,∠ACD=∠B
∴△ACD∽△CBD
∴AC:CB=AD:DC
在Rt△ADC中,同理AD:DC=AE:ED,
∴AE:ED=AC:CB=4:5
故此题应该填4:5.
20.解:因为第一个中点三角形与△ABC相似,所以根据三角形中位线定理得到相似比是,面积的比是相似比的平方是.则第一个中点三角形的周长是△ABC的周长的,同理,第二个中点三角形的周长是第一个的,即△ABC的周长的,第三个是△ABC的周长的;第n个是与△ABC周长的比;同理,面积的比是.
三.解答题
21.解:由于P为线段AB=10cm的黄金分割点,
则AP=10×=5﹣5或AP=10×=15﹣5.
故AP的长为:(5﹣5)cm或(15﹣5)cm.
22.解:设===k(k≠0),则a+2b=7k,3b﹣2c=5k,c﹣2a=3k,
∴a=﹣,b=k,c=k,
∴==.
23.解:(1)过D作DE∥AC,交BF于点E,
∴∠PDE=∠PAF,
∵P是AD的中点,
∴AP=DP,
∵在△PDE和△PAF中,
,
∴△PDE≌△PAF(ASA),
∴PE=PF,
由DE∥AC,得到=,
∵AD是△ABC的中线,
∴BD=DC,
∴BE=EF=2PF,
∴BP=3PF;
(2)∵△PDE≌△PAF,
∴DE=AF,
∴==,
∴AF=AC=×12=4.
24.证明:∵=,∠A=∠A,
∴△BAD∽△CAE,
∴∠B=∠C,
∵∠BOE=∠DOC,
∴△BOE∽△DOC,
∴=,
∴OB?OD=OC?OE.
25.解:AB==,BC=10,AC==,
AE=2,AD=,DE==,CE==,
BD==,
∴===,
===,
∴△ABC∽△ADE,△ABD∽△ACE.
26.解:
(1)纵坐标均增加4,横坐标均不变;
(2)纵坐标不变,横坐标变为原横坐标的相反数;
(3)点C对应点的横坐标增加2个单位,纵坐标增加3个单位,点B对应点的横坐标增加2个单位而纵坐标不变.
27.解:如图,
∵∠1=∠2,
∠SAB=∠PCB,
∴△SAB∽△PBC,
即=,
SA=×PC=24×=12厘米.
故点光源S到平面镜的距离SA的长度是12厘米.
图形的相似》单元测试题
一.选择题
1.已知mn=ef,则下列式子错误的是( )
A.
B.
C.
D.
2.小明的数学作业本的纸上都是等距离的横线,他在上面任意画一条不与这些横线平行的直线,那么这条直线被这些横线所截得的线段( )
A.平行
B.相等
C.平行或相等
D.不相等
3.在相同水压下,口径为4cm的水管的出水量是口径为1cm的水管出水量的( )
A.4倍
B.8倍
C.12倍
D.16倍
4.已知:△ABC∽△DEF相似,,那么△ABC和△DEF的相似比是( )
A.
B.
C.
D.
5.如图,∠CAB=∠CBD,AB=4,AC=6,BD=7.5,BC=5,则CD的长为( )
A.
B.1
C.3.5
D.6
6.在某一时刻测得1米高的竹竿的影长为0.9米,同时测得一棵树的影长,落在地面上的影长为1.8米,落在墙上的影长为0.4米,则这棵树的高度为( )
A.2米
B.2.4米
C.2.2米
D.2.8米
7.若x、y为非零线段的长,则下列说法错误的是( )
A.若=,则=
B.若=,则=
C.若=,则=
D.若2x﹣5y=0,则=
8.如图,在△ABC中,AB=AC=8,∠A=36°,BD平分∠ABC交AC于点D,则AD=( )
A.4
B.4﹣4
C.﹣4+4
D.4﹣4或﹣4+4
9.如图,∠AOD=90°,OA=OB=BC=CD,那么下列结论成立的是( )
A.△OAB∽△OCA
B.△OAB∽△ODA
C.△BAC∽△BDA
D.以上结论都不成立
10.如果一个图形上各点的横坐标保持不变,而纵坐标分别都变化为原来的,那么所得的图形与原图形相比( )
A.形状不变,图形缩小为原来的一半
B.形状不变,图形放大为原来的2倍
C.整个图形被横向压缩为原来的一半
D.整个图形被纵向压缩为原来的一半
二.填空题
11.某人背对路灯离路灯1m处时,影长为2m,他再往前走2m时,影长为
m.
12.在Rt△ABC中,AD是斜边上的高,若AB=,DC=2,则BD=
,AC=
.
13.如图,添上条件
,则△ABC∽△ADE.
14.如图,梯形ABCD中,DC∥EF∥AB,AC交EF于G.若AE=2ED,CF=2cm,AG=5cm,则BC=
cm,CG=
cm.
15.若线段AB上黄金分割点为C,且AC<BC,又AB的长为4cm,则CB的长为
cm.
16.已知,那么=
.
17.如图,△ABC与△DEF是位似三角形,且AC=2DF,则OE:OB=
.
18.在方格纸中,每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.如图,请你在4×4的方格纸中,画一个格点三角形A1B1C1,使△A1B1C1与格点三角形ABC相似(相似比不为1).
.
19.如图,Rt△ABC中,CD是斜边上的高,DE⊥AC于E,AC:CB=4:5,则AE:ED等于
.
20.已知△ABC,取三边中点,连接三个中点构成第一个中点三角形,再取第一个中点三角形三边中点,连接三个中点得到第二个中点三角形…依此类推,当得到第n个中点三角形时,所有这些三角形都相似,此时第n个中点三角形与△ABC周长的比是
,面积的比是
.
三.解答题
21.线段AB的长度为10cm,点P为其一个黄金分割点,求AP的长.
22.已知==,求的值.
23.如图,AD是△ABC的中线,P是AD的中点,延长BP交AC于点F.
(1)试说明PB=3PF;
(2)若AC的长为12,求AF的长.
24.如图,已知=,试说明OB?OD=OC?OE.
25.在边长为1的正方形网格中有A、B、C、D、E五个点,问△ABC与△ADE是否相似?为什么?由此,你还能找出图中相似的三角形吗?若能,请找出来,并说明理由.
26.将△ABC作下列变化,请画出相应的图形,并指出三个顶点的坐标所发生的变化.
(1)向上平移4个单位;
(2)关于y轴对称;
(3)以A点为位似中心,相似比为2.
27.点光源S在平面镜上方,若在点P处可以看到点光源的反射光线,并测得AB=10厘米,BC=20厘米,PC⊥AB,且PC=24厘米,试求点光源S到平面镜的距离SA的长度.
参考答案与试题解析
一.选择题
1.解:根据比例的基本性质,
所给选项中,只有B项经转换后为等积式是me=nf,和已知不符,错误.
故选:B.
2.解:根据平行线等分线段定理,得这条直线被横线所截得的线段相等.故选B.
3.解:水管的截面是圆,两个圆是相似图形,它们的口径分别是4cm和1cm,得到相似比为4:1,所以面积的比是16:1.
所以出水量的比为16:1.
故选:D.
4.解:因为△ABC∽△DEF相似,且,
所以△ABC和△DEF的相似比,故选A.
5.解:∵AB=4,AC=6,BD=7.5,BC=5,
∴=,
∵∠CAB=∠CBD,
∴△ABC∽△BCD,
∴=,
∴CD=BC=×5=.
故选:A.
6.解:设影长为1.8m时树的高度为hm,
∵在某一时刻测得直立的标杆长0.9m,其影长为1m,
∴,
解得x=2m,
∴树的高度=2+0.4=2.4m,
答:树的高度是2.4米.
故选:B.
7.解:A、若=,则=,故此选项正确;
B、若=,则=,∴=,=,∴=,故此选项正确;
C、若=,则=,∴=,故此选项正确;
D、若2x﹣5y=0,则x=y,∴==,故此选项错误;
故选:D.
8.解:∵AB=AC=8,
∴∠ABC=∠C=(180°﹣∠A)=(180°﹣36°)=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=∠ABC=36°,
∴∠A=∠ABD,
∴AD=BD,
∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴BD=BC,
∴AD=BD=BC,
∴∠A=∠CBD,∠C=∠C,
∴△ABC∽△BCD,
∴AC:BC=BC:CD,
∴AC:AD=AD:CD,
∴点D为AC的黄金分割点,
∴AD=AC=×8=4()=4.
故选:B.
9.解:∵∠AOD=90°,设OA=OB=BC=CD=x
∴AB=x,AC=x,AD=x,OC=2x,OD=3x,BD=2x
∴,,
∴
∴△BAC∽△BDA
故选:C.
10.解:∵一个图形上各点的横坐标保持不变,而纵坐标分别都变化为原来的,
∴整个图形被纵向压缩为原来的一半
故选:D.
二.填空题
11.解:∵人身高:路灯高=影长:影长与到路灯距离之和,设再走2m时,影长为x
∴人身高:路灯高=2:(2+1)=x:(x+2+1)
解得影长x=6(m)
故他再往前走2m时,影长为6m.
12.解:根据射影定理可得:AB2=BD×BC;AC2=CD×BC,
∴解得:BD=1,AC=.
故答案为:1,.
13.解:∵∠A=∠A
∴当BC∥DE或∠ABC=∠ADE或时,△ABC∽△ADE.
14.解:∵DC∥EF∥AB,
∴==2,又AG=5cm,
∴GC=2.5cm.
=,CF=2cm,
∴BC=6cm.
故答案为:6,2.5.
15.解:根据黄金分割点的概念得:CB=AB=2﹣2.
故本题答案为:2﹣2.
16.解:∵=,
∴设a=3k,b=2k,
则==5.
故答案为:5.
17.解:∵△ABC与△DEF是位似三角形,
∴DF∥AC,EF∥BC
∴△OAC∽△ODF,OE:OB=OF:OC
∴OF:OC=DF:AC
∵AC=2DF
∴OE:OB=DF:AC=1:2.
故答案为:1:2.
18.解:如图所示:
19.解:在Rt△ACB中,
∵∠A+∠B=90°,∠A+∠ACD=90°,∠B+∠BCD=90°
∴∠A=∠DCB,∠ACD=∠B
∴△ACD∽△CBD
∴AC:CB=AD:DC
在Rt△ADC中,同理AD:DC=AE:ED,
∴AE:ED=AC:CB=4:5
故此题应该填4:5.
20.解:因为第一个中点三角形与△ABC相似,所以根据三角形中位线定理得到相似比是,面积的比是相似比的平方是.则第一个中点三角形的周长是△ABC的周长的,同理,第二个中点三角形的周长是第一个的,即△ABC的周长的,第三个是△ABC的周长的;第n个是与△ABC周长的比;同理,面积的比是.
三.解答题
21.解:由于P为线段AB=10cm的黄金分割点,
则AP=10×=5﹣5或AP=10×=15﹣5.
故AP的长为:(5﹣5)cm或(15﹣5)cm.
22.解:设===k(k≠0),则a+2b=7k,3b﹣2c=5k,c﹣2a=3k,
∴a=﹣,b=k,c=k,
∴==.
23.解:(1)过D作DE∥AC,交BF于点E,
∴∠PDE=∠PAF,
∵P是AD的中点,
∴AP=DP,
∵在△PDE和△PAF中,
,
∴△PDE≌△PAF(ASA),
∴PE=PF,
由DE∥AC,得到=,
∵AD是△ABC的中线,
∴BD=DC,
∴BE=EF=2PF,
∴BP=3PF;
(2)∵△PDE≌△PAF,
∴DE=AF,
∴==,
∴AF=AC=×12=4.
24.证明:∵=,∠A=∠A,
∴△BAD∽△CAE,
∴∠B=∠C,
∵∠BOE=∠DOC,
∴△BOE∽△DOC,
∴=,
∴OB?OD=OC?OE.
25.解:AB==,BC=10,AC==,
AE=2,AD=,DE==,CE==,
BD==,
∴===,
===,
∴△ABC∽△ADE,△ABD∽△ACE.
26.解:
(1)纵坐标均增加4,横坐标均不变;
(2)纵坐标不变,横坐标变为原横坐标的相反数;
(3)点C对应点的横坐标增加2个单位,纵坐标增加3个单位,点B对应点的横坐标增加2个单位而纵坐标不变.
27.解:如图,
∵∠1=∠2,
∠SAB=∠PCB,
∴△SAB∽△PBC,
即=,
SA=×PC=24×=12厘米.
故点光源S到平面镜的距离SA的长度是12厘米.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
