六年级下册数学课件-2.1 圆柱的体积 西师大版(共51张PPT)
文档属性
| 名称 | 六年级下册数学课件-2.1 圆柱的体积 西师大版(共51张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 689.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 00:00:00 | ||
图片预览








文档简介
(共51张PPT)
六年级下册第二单元
圆柱的体积
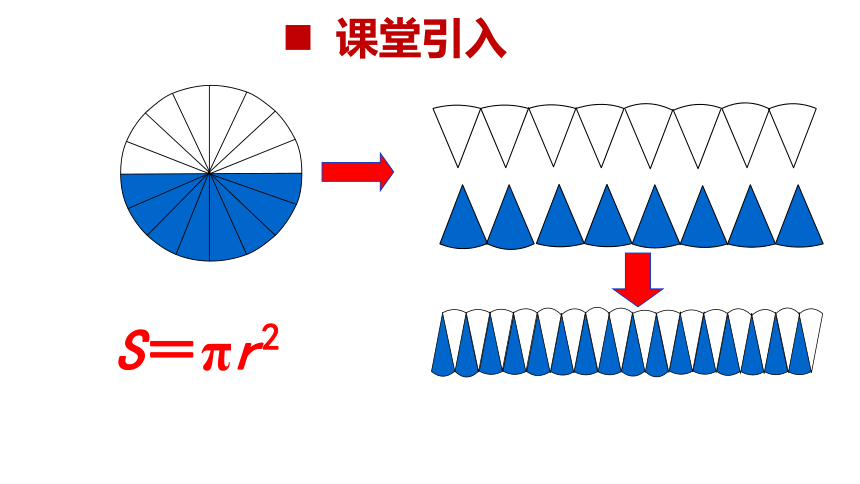
课堂引入
S=πr2
v
长
=a
b
h
v
3
正
=a
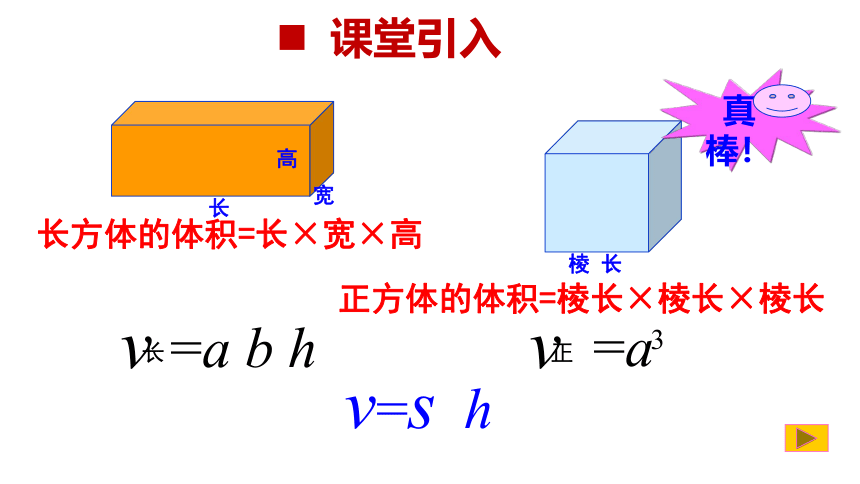
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
v=s
h
长
宽
高
棱
长
真
棒!
课堂引入
圆柱体积的大小与哪些条件有关?
底面积
高
课堂探索
怎样计算圆柱的体积呢?
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
自学指导
1、以小组为单位,把圆柱体的底面平均分成若干个扇形,再纵切成相等的两部分,再把它们拼成一个近似的长方体。
2、议一议:拼成的长方体与原来的圆柱体的底面积的大小有什么关系?高的大小有什么关系?体积的大小有什么关系?
3、根据这些关系,你能推出圆柱的体积计算公式吗?
(分一分
拼一拼
议一议)
底面积
课堂探索
长方体的体积=底面积×高
底面积
长方体的体积=底面积×高
课堂探索
底面积
长方体的体积=底面积×高
课堂探索
高
圆柱的体积=
×
底面积
课堂探索
长方体的体积=底面积×高
把圆柱切割拼成近似(
),它们的(
)相等。长方体的高就是圆柱的(
),长方体的底面积就是圆柱的(
),因为长方体的体积=(
),所以圆柱的体积=(
)。用字母“V
”表示( ),“S
”表示(
),“h”表示( ),那么,圆柱的体积用字母表示为( )。
长方体
体积
高
底面积
底面积×高
底面积×高
体积
底面积
高
v
=sh
课堂练习——填一填
(1)
(2)
(3)
看图列式,并写出相应的公式。
v=s
h
12×6
3.14
×3
×7
2
3.14
×(6÷2)
×8
2
6dm
12dm2
7dm
.
3dm
6dm
8dm
V=兀(d÷2)×h
2
V=
兀r2
×
h
课堂探索
(1)已知底面半径和高,怎样求圆柱的体积?
(2)已知底面直径和高,怎样求圆柱的体积?
(3)已知底面周长和高,怎样求圆柱的体积?
课堂探索——讨论
(1)已知底面半径和高:
(2)已知底面直径和高:
(3)已知底面周长和高:
V=πr2h
V=π(
)2h
d
2
V=π(C÷d÷2
)2h
课堂探索——讨论
一根圆柱形钢材,底面积是28.6cm2,高是15cm。它的体积是多少?
圆柱体积=底面积×高
28.6×15=429(cm3)
答:它的体积是429cm3
。
试
一
试
课堂练习
一个压路机的前轮是圆柱,轮宽2.5m,半径1m,它的体积是多少立方米?
3.14×12×2.5
=3.14×2.5
=7.85(m3)
答:它的体积是7.85m3。
拓展训练
通过这节课的学习,你学到了什么?
课堂总结
讨论
(1)已知底面半径和高:
(2)已知底面直径和高:
(3)已知底面周长和高:
V=πr2h
V=π(
)2h
d
2
V=π(C÷
π
÷2
)2h
圆柱的体积=底面积×高
V
=s
h
课堂总结
再见!!!
六年级下册第二单元
圆柱的体积
课堂引入
S=πr2
v
长
=a
b
h
v
3
正
=a
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
v=s
h
长
宽
高
棱
长
真
棒!
课堂引入
圆柱体积的大小与哪些条件有关?
底面积
高
课堂探索
怎样计算圆柱的体积呢?
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
课堂探索
自学指导
1、以小组为单位,把圆柱体的底面平均分成若干个扇形,再纵切成相等的两部分,再把它们拼成一个近似的长方体。
2、议一议:拼成的长方体与原来的圆柱体的底面积的大小有什么关系?高的大小有什么关系?体积的大小有什么关系?
3、根据这些关系,你能推出圆柱的体积计算公式吗?
(分一分
拼一拼
议一议)
底面积
课堂探索
长方体的体积=底面积×高
底面积
长方体的体积=底面积×高
课堂探索
底面积
长方体的体积=底面积×高
课堂探索
高
圆柱的体积=
×
底面积
课堂探索
长方体的体积=底面积×高
把圆柱切割拼成近似(
),它们的(
)相等。长方体的高就是圆柱的(
),长方体的底面积就是圆柱的(
),因为长方体的体积=(
),所以圆柱的体积=(
)。用字母“V
”表示( ),“S
”表示(
),“h”表示( ),那么,圆柱的体积用字母表示为( )。
长方体
体积
高
底面积
底面积×高
底面积×高
体积
底面积
高
v
=sh
课堂练习——填一填
(1)
(2)
(3)
看图列式,并写出相应的公式。
v=s
h
12×6
3.14
×3
×7
2
3.14
×(6÷2)
×8
2
6dm
12dm2
7dm
.
3dm
6dm
8dm
V=兀(d÷2)×h
2
V=
兀r2
×
h
课堂探索
(1)已知底面半径和高,怎样求圆柱的体积?
(2)已知底面直径和高,怎样求圆柱的体积?
(3)已知底面周长和高,怎样求圆柱的体积?
课堂探索——讨论
(1)已知底面半径和高:
(2)已知底面直径和高:
(3)已知底面周长和高:
V=πr2h
V=π(
)2h
d
2
V=π(C÷d÷2
)2h
课堂探索——讨论
一根圆柱形钢材,底面积是28.6cm2,高是15cm。它的体积是多少?
圆柱体积=底面积×高
28.6×15=429(cm3)
答:它的体积是429cm3
。
试
一
试
课堂练习
一个压路机的前轮是圆柱,轮宽2.5m,半径1m,它的体积是多少立方米?
3.14×12×2.5
=3.14×2.5
=7.85(m3)
答:它的体积是7.85m3。
拓展训练
通过这节课的学习,你学到了什么?
课堂总结
讨论
(1)已知底面半径和高:
(2)已知底面直径和高:
(3)已知底面周长和高:
V=πr2h
V=π(
)2h
d
2
V=π(C÷
π
÷2
)2h
圆柱的体积=底面积×高
V
=s
h
课堂总结
再见!!!
