18.1.1平行四边形的性质 课件(17张)
文档属性
| 名称 | 18.1.1平行四边形的性质 课件(17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 331.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 00:00:00 | ||
图片预览





文档简介
18.1.1平行四边形的性质
你能利用手中两张全等的三角形纸片将它们相等的一组边重合拼出四边形吗?一共可以拼出几种?
拼一拼
拼出的效果图有以下6种:
拼一拼
观察拼出的四边形它们的对边有怎样的位置关系?说说你的理由.
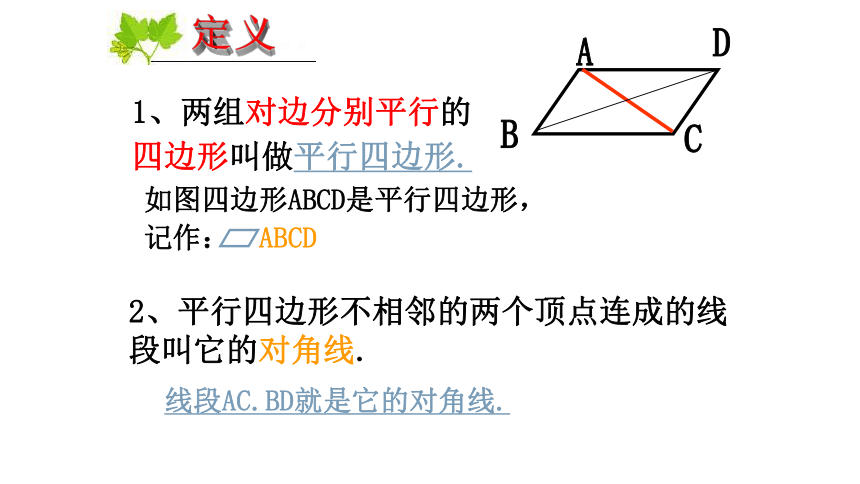
1、两组对边分别平行的
四边形叫做平行四边形.
如图四边形ABCD是平行四边形,
记作: ABCD
A
B
C
D
2、平行四边形不相邻的两个顶点连成的线段叫它的对角线.
定义
线段AC.BD就是它的对角线.
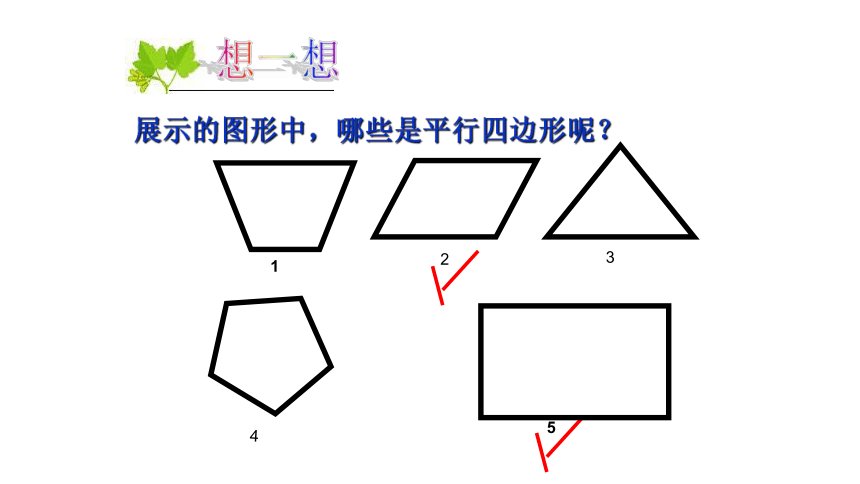
想一想
展示的图形中,哪些是平行四边形呢?
2
3
1
4
5
画一画
根据定义画一个平行四边形.
平行四边形的边与边、角与角之间有怎样的数量关系?
A
B
C
D
猜一猜
开放探究平行四边形的性质
活动
活动要求 :
可以采用度量、平移、旋转、折叠,拼图等方法,通过小组合作探究平行四边形有哪些性质(边与边,角与角);结论写在白纸上.
已知:如图平行四边形ABCD,求证:AB=CD,BC=AD,∠B=∠D,∠BAD=∠BCD
证明:连接AC,
∵ AB∥CD,AD∥BC,
∴ ∠1=∠3,∠2=∠4.
又 AC=CA,
∴ △ABC≌△CDA (ASA).
∴ AB=CD,CB=AD,∠B=∠D.
又 ∠1+∠4=∠2+∠3,
∴ ∠BAD=∠BCD.
证一证
平行四边形的性质:
A
B
C
D
文字叙述
几何语言
对边平行
AB∥DC ,AD∥BC
对边相等
AB=DC ,AD=BC
邻角互补
∠A +∠ B =180°……
边
角
∠A=∠C ,∠B=∠D
对角相等
例题讲解
例1.已知:平行四边形ABCD,
BD为对角线(如图)∠A=70°, ∠BDC=30°, AD=15,求:∠C,
∠ADB的度数, 并求BC边的长.
解: ∵四边形ABCD是平行四边形
∴∠C=∠A=70°
∠ADC=180°- 70°= 110°
又∵ ∠BDC=30°
∴ ∠ADB = 80°
而 BC = AD = 15
已知在 ABCD中,∠A=60°,BC=3cm,则∠B=_____,∠C=_____,AD=_____.
A
B
C
D
60°
3cm
120°
比一比看谁做题规范
练习1
如图:四边形ABCD是平行四边形,四条边中哪些线段可以通过平移而相互得到?
C
B
A
D
结论:平行四边形的对边平行且相等.
练习2
你学到了什么?
ABCD
② 角
① 边
对边平行且相等
对角相等
邻角互补
知识点(一):定义及表示方法.
知识点(二):性质
知识总结
1.必做题:教材P43:练习1、2
2.选做题:
(1)已知平行四边形ABCD中, ∠1=15°, ∠2=25°,且AB=5cm,AO=2cm,求∠DAB和∠ABC的度数,并找出长度分别为5cm和2cm的线段.
(2)在平行四边形ABCD中, DB⊥AD, AD=6cm, 平行四边形ABCD的面积为24, 求平行四边形ABCD的周长.
作业
你能利用手中两张全等的三角形纸片将它们相等的一组边重合拼出四边形吗?一共可以拼出几种?
拼一拼
拼出的效果图有以下6种:
拼一拼
观察拼出的四边形它们的对边有怎样的位置关系?说说你的理由.
1、两组对边分别平行的
四边形叫做平行四边形.
如图四边形ABCD是平行四边形,
记作: ABCD
A
B
C
D
2、平行四边形不相邻的两个顶点连成的线段叫它的对角线.
定义
线段AC.BD就是它的对角线.
想一想
展示的图形中,哪些是平行四边形呢?
2
3
1
4
5
画一画
根据定义画一个平行四边形.
平行四边形的边与边、角与角之间有怎样的数量关系?
A
B
C
D
猜一猜
开放探究平行四边形的性质
活动
活动要求 :
可以采用度量、平移、旋转、折叠,拼图等方法,通过小组合作探究平行四边形有哪些性质(边与边,角与角);结论写在白纸上.
已知:如图平行四边形ABCD,求证:AB=CD,BC=AD,∠B=∠D,∠BAD=∠BCD
证明:连接AC,
∵ AB∥CD,AD∥BC,
∴ ∠1=∠3,∠2=∠4.
又 AC=CA,
∴ △ABC≌△CDA (ASA).
∴ AB=CD,CB=AD,∠B=∠D.
又 ∠1+∠4=∠2+∠3,
∴ ∠BAD=∠BCD.
证一证
平行四边形的性质:
A
B
C
D
文字叙述
几何语言
对边平行
AB∥DC ,AD∥BC
对边相等
AB=DC ,AD=BC
邻角互补
∠A +∠ B =180°……
边
角
∠A=∠C ,∠B=∠D
对角相等
例题讲解
例1.已知:平行四边形ABCD,
BD为对角线(如图)∠A=70°, ∠BDC=30°, AD=15,求:∠C,
∠ADB的度数, 并求BC边的长.
解: ∵四边形ABCD是平行四边形
∴∠C=∠A=70°
∠ADC=180°- 70°= 110°
又∵ ∠BDC=30°
∴ ∠ADB = 80°
而 BC = AD = 15
已知在 ABCD中,∠A=60°,BC=3cm,则∠B=_____,∠C=_____,AD=_____.
A
B
C
D
60°
3cm
120°
比一比看谁做题规范
练习1
如图:四边形ABCD是平行四边形,四条边中哪些线段可以通过平移而相互得到?
C
B
A
D
结论:平行四边形的对边平行且相等.
练习2
你学到了什么?
ABCD
② 角
① 边
对边平行且相等
对角相等
邻角互补
知识点(一):定义及表示方法.
知识点(二):性质
知识总结
1.必做题:教材P43:练习1、2
2.选做题:
(1)已知平行四边形ABCD中, ∠1=15°, ∠2=25°,且AB=5cm,AO=2cm,求∠DAB和∠ABC的度数,并找出长度分别为5cm和2cm的线段.
(2)在平行四边形ABCD中, DB⊥AD, AD=6cm, 平行四边形ABCD的面积为24, 求平行四边形ABCD的周长.
作业
