3.2图形的旋转课件(第2课时 22张)
文档属性
| 名称 | 3.2图形的旋转课件(第2课时 22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 913.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 21:48:55 | ||
图片预览



文档简介
3.2图形的旋转
第2课时
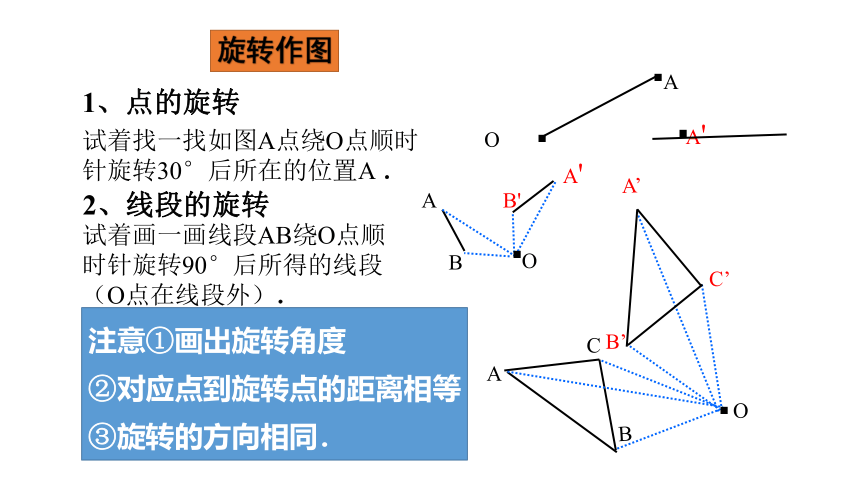
1、点的旋转
A
O
A'
2、线段的旋转
A
A'
O
B
B'
3、图形的旋转
A’
B’
C’
A
B
C
O
试着找一找如图A点绕O点顺时针旋转30°后所在的位置A .
试着画一画线段AB绕O点顺时针旋转90°后所得的线段(O点在线段外).
试着画△ABC绕O点逆时针旋转60°后所得的三角形.
——自主观察
.
.
.
.
.
知识点
旋转作图
注意①画出旋转角度
②对应点到旋转点的距离相等
③旋转的方向相同.
解:(1)以AB为一边按顺时针方向画∠BAX,使得∠BAX=60°.
(2)在射线AX上取点C,使得AC=AB.
线段AC就是线段AB绕点A按顺时针方向旋转60°后的线段.
X
.
C
在图中,画出线段AB绕点A按顺时针方向旋转60°后的线段.
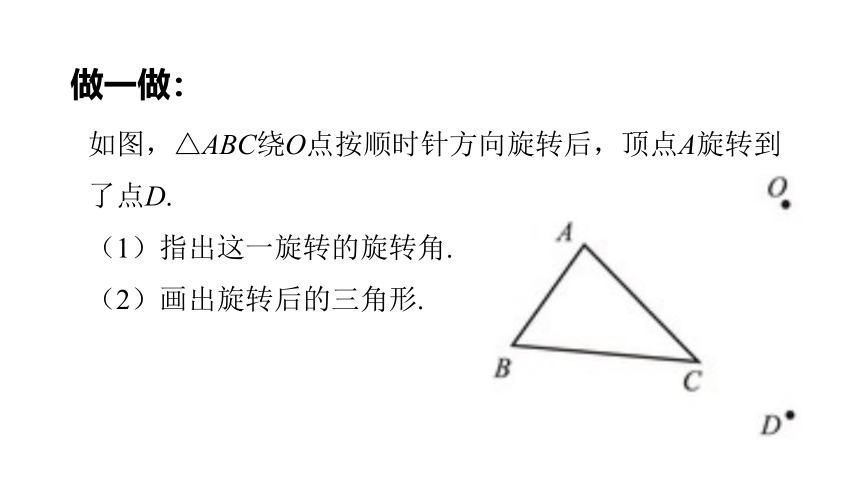
做一做:
如图,△ABC绕O点按顺时针方向旋转后,顶点A旋转到了点D.
(1)指出这一旋转的旋转角.
(2)画出旋转后的三角形.
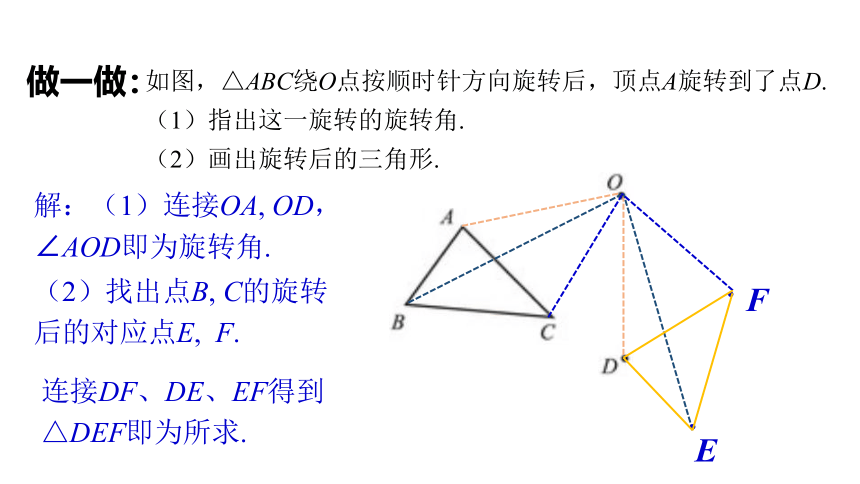
做一做:
解:(1)连接OA, OD,∠AOD即为旋转角.
(2)找出点B, C的旋转后的对应点E, F.
.
.
E
F
连接DF、DE、EF得到△DEF即为所求.
做一做:
如图,△ABC绕O点按顺时针方向旋转后,顶点A旋转到了点D.
(1)指出这一旋转的旋转角.
(2)画出旋转后的三角形.
目标检测1:
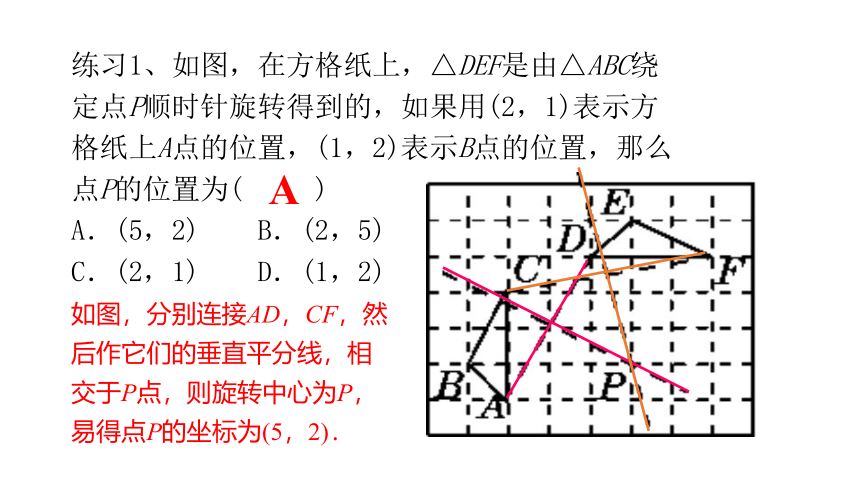
练习1、如图,在方格纸上,△DEF是由△ABC绕定点P顺时针旋转得到的,如果用(2,1)表示方格纸上A点的位置,(1,2)表示B点的位置,那么点P的位置为( )
A.(5,2) B.(2,5)
C.(2,1) D.(1,2)
A
如图,分别连接AD,CF,然后作它们的垂直平分线,相交于P点,则旋转中心为P,易得点P的坐标为(5,2).
2.如图,四边形ABCD经过旋转后与四边形ADEF重合.则下列结论:①AB=AD=AF;②BC=CD;③CD=EF;④∠B=∠F;⑤∠BAD=∠CAE=∠DAF;⑥∠BCD=∠DEF.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在6×4的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
A.格点M B.格点N
C.格点P D.格点Q
D
B
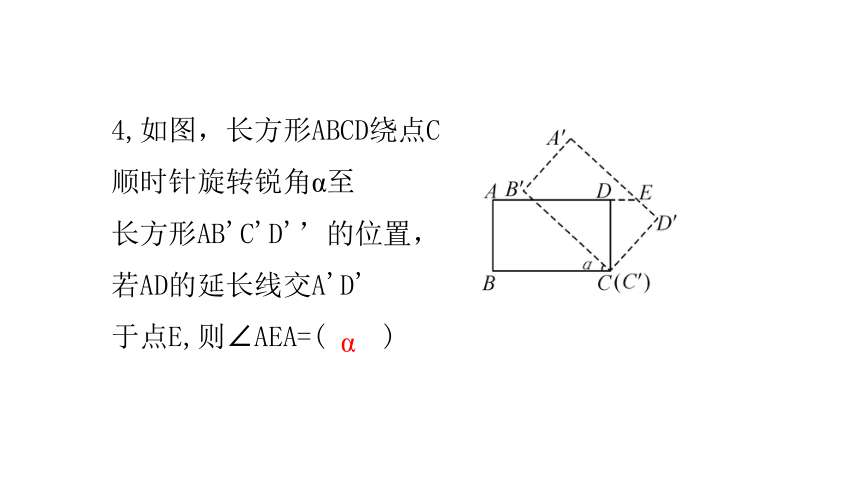
4,如图,长方形ABCD绕点C顺时针旋转锐角α至
长方形AB'C'D'’的位置,若AD的延长线交A'D'
于点E,则∠AEA=( )
α
知识点
做一做:
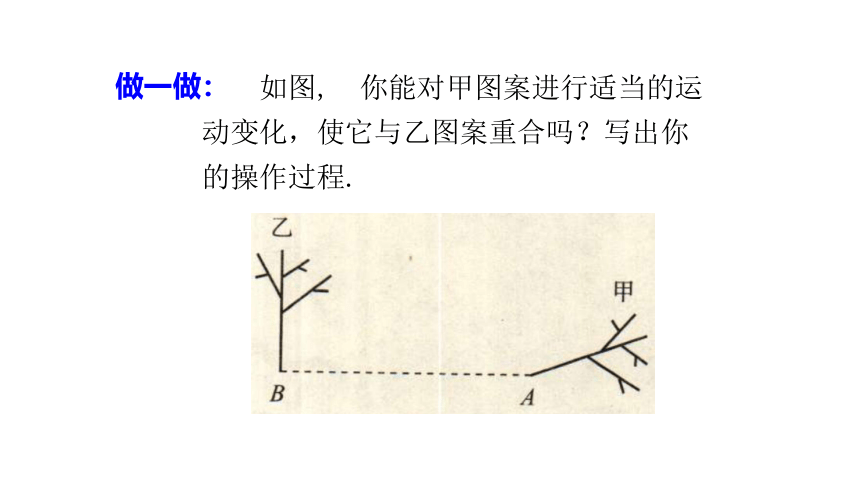
如图, 你能对甲图案进行适当的运动变化,使它与乙图案重合吗?写出你的操作过程.
怎样将甲图案变成乙图案?
甲
甲
乙
乙
A
B
B
A
可以先将甲图案绕图上的A点旋转,使得图案被“扶直”,然后,再沿AB方向将所得图案平移到B点位置,即可得到乙图案
还可以用什么方法把甲图案变成乙图案?
知识点
平移、 旋转相结合:
先平移
后旋转
下图由四部分组成,每部分都包括两个小”十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?
O
整个图形可以看作是左边的两个小“十字”先通过一次平移成图形右侧的部分,然后左、右部分一起绕图形的中心旋转90°前后图形组成的。
知识点
轴对称:
下图由四部分组成,每部分都包括两个小”十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?
直线EF与GH相交于图形的中心O,且互相垂直,先把左边的两个“十字”作关于EF的轴对称图形,然后作这两部分关于GH的轴对称图形,这样就可以得到整个图形。
E
F
G
H
O
知识点
例1 如图所示,已知△ACB与△DFE是两个全等的直角三角形,量得它们的斜边长为10 cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B,C,F,D在一条直线上,且点C与点F重合,将图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC交DE于点G,求线段FG的长(结果保留根号).
分析:根据图形旋转的特征,找出对应线段相等、对应角相等是解决问题的关键.
解:∵BC=EF,∠B=60°,
∴△BCE是等边三角形.
∴∠AFE=30°.
∴∠GFD=60°.
又∠D=∠A=30°,
∴∠FGD=90°.
在Rt△DEF中,DE=AB=10 cm,
确定旋转中心与旋转角的方法:
在图形的旋转过程中,判断谁是旋转中心,要看旋转中心是在图形上还是不在图形上;若在图形
上,哪一点在旋转过程中位置没有改变,这一点就
是旋转中心;若不在图形上,对应点连线的垂直平
分线的交点就是旋转中心,旋转角等于对应点与旋
转中心所连线段的夹角.
总 结
1.如图,在直角梯形ABCD中,AD // BC,AD= 3,
BC=5,将腰DC绕点D逆时针方向旋转90°至DE,连接AE,则△ADE的面积是( )
3
课后作业
2.如图所示,已知正三角形ABC内有一点P,PA=6,PB=8,PC=10,求∠APB的大小.
分析:将△BCP绕点B逆时针旋转60°,点C和点A重合,点P旋转到点P',连接PP',得正三角形PBP',从而可知∠BPP'=60°,推出Rt△APP',求出∠APP',即可求出∠APB的大小.
2.如图所示,已知正三角形ABC内有一点P,PA=6,PB=8,PC=10,求∠APB的大小.
解:将△BCP绕点B逆时针旋转60°,点C和A重合,点P旋转到点P',连接PP'.
∵∠PBP'=60°,BP=BP',
∴△PBP'是正三角形.
∴∠BPP'=60°,P'P=BP=8.
由旋转知,AP'=PC=10,
又PA=6,∴PP'2+PA2=AP'2.
∴∠APP'=90°.
∴∠APB=60°+90°=150°.
3.如图,△ABC为等腰直角三角形,而△AFC是由△ABD按顺时针方向旋转而来的,如果BD=EC.
(1)△AFC是由△ABD旋转多少度得到的?旋转中心在哪里?
(2)∠FCE为多少度?
解:(1)△AFC是由△ABD顺时针旋转270°得到的.旋转中心是点A.
(2)∵△ABC为等腰直角三角形,
∴∠ABD=∠ACE=∠ACF=45°,
∴∠FCE=90°.
4. 如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转变换得到的.
(1)请写出旋转中心的坐标是________,旋转角是________°;
(2)以(1)中的旋转中心为中心,分别画出将△A1AC1顺时针旋转90°,180°的三角形;
(3)设Rt△ABC的两直角边BC=a,AC=b,斜边AB=c,利用变换前后所形成的图案证明勾股定理.
.
4. 如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转变换得到的.
(2)以(1)中的旋转中心为中心,分别画出将△A1AC1顺时针旋转90°,180°的三角形;
(3)设Rt△ABC的两直角边BC=a,AC=b,斜边AB=c,利用变换前后所形成的图案证明勾股定理.
(2)解:图形如图.
4. 如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转变换得到的.
(3)设Rt△ABC的两直角边BC=a,AC=b,斜边AB=c,利用变换前后所形成的图案证明勾股定理.
第2课时
1、点的旋转
A
O
A'
2、线段的旋转
A
A'
O
B
B'
3、图形的旋转
A’
B’
C’
A
B
C
O
试着找一找如图A点绕O点顺时针旋转30°后所在的位置A .
试着画一画线段AB绕O点顺时针旋转90°后所得的线段(O点在线段外).
试着画△ABC绕O点逆时针旋转60°后所得的三角形.
——自主观察
.
.
.
.
.
知识点
旋转作图
注意①画出旋转角度
②对应点到旋转点的距离相等
③旋转的方向相同.
解:(1)以AB为一边按顺时针方向画∠BAX,使得∠BAX=60°.
(2)在射线AX上取点C,使得AC=AB.
线段AC就是线段AB绕点A按顺时针方向旋转60°后的线段.
X
.
C
在图中,画出线段AB绕点A按顺时针方向旋转60°后的线段.
做一做:
如图,△ABC绕O点按顺时针方向旋转后,顶点A旋转到了点D.
(1)指出这一旋转的旋转角.
(2)画出旋转后的三角形.
做一做:
解:(1)连接OA, OD,∠AOD即为旋转角.
(2)找出点B, C的旋转后的对应点E, F.
.
.
E
F
连接DF、DE、EF得到△DEF即为所求.
做一做:
如图,△ABC绕O点按顺时针方向旋转后,顶点A旋转到了点D.
(1)指出这一旋转的旋转角.
(2)画出旋转后的三角形.
目标检测1:
练习1、如图,在方格纸上,△DEF是由△ABC绕定点P顺时针旋转得到的,如果用(2,1)表示方格纸上A点的位置,(1,2)表示B点的位置,那么点P的位置为( )
A.(5,2) B.(2,5)
C.(2,1) D.(1,2)
A
如图,分别连接AD,CF,然后作它们的垂直平分线,相交于P点,则旋转中心为P,易得点P的坐标为(5,2).
2.如图,四边形ABCD经过旋转后与四边形ADEF重合.则下列结论:①AB=AD=AF;②BC=CD;③CD=EF;④∠B=∠F;⑤∠BAD=∠CAE=∠DAF;⑥∠BCD=∠DEF.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在6×4的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
A.格点M B.格点N
C.格点P D.格点Q
D
B
4,如图,长方形ABCD绕点C顺时针旋转锐角α至
长方形AB'C'D'’的位置,若AD的延长线交A'D'
于点E,则∠AEA=( )
α
知识点
做一做:
如图, 你能对甲图案进行适当的运动变化,使它与乙图案重合吗?写出你的操作过程.
怎样将甲图案变成乙图案?
甲
甲
乙
乙
A
B
B
A
可以先将甲图案绕图上的A点旋转,使得图案被“扶直”,然后,再沿AB方向将所得图案平移到B点位置,即可得到乙图案
还可以用什么方法把甲图案变成乙图案?
知识点
平移、 旋转相结合:
先平移
后旋转
下图由四部分组成,每部分都包括两个小”十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?
O
整个图形可以看作是左边的两个小“十字”先通过一次平移成图形右侧的部分,然后左、右部分一起绕图形的中心旋转90°前后图形组成的。
知识点
轴对称:
下图由四部分组成,每部分都包括两个小”十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?
直线EF与GH相交于图形的中心O,且互相垂直,先把左边的两个“十字”作关于EF的轴对称图形,然后作这两部分关于GH的轴对称图形,这样就可以得到整个图形。
E
F
G
H
O
知识点
例1 如图所示,已知△ACB与△DFE是两个全等的直角三角形,量得它们的斜边长为10 cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B,C,F,D在一条直线上,且点C与点F重合,将图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC交DE于点G,求线段FG的长(结果保留根号).
分析:根据图形旋转的特征,找出对应线段相等、对应角相等是解决问题的关键.
解:∵BC=EF,∠B=60°,
∴△BCE是等边三角形.
∴∠AFE=30°.
∴∠GFD=60°.
又∠D=∠A=30°,
∴∠FGD=90°.
在Rt△DEF中,DE=AB=10 cm,
确定旋转中心与旋转角的方法:
在图形的旋转过程中,判断谁是旋转中心,要看旋转中心是在图形上还是不在图形上;若在图形
上,哪一点在旋转过程中位置没有改变,这一点就
是旋转中心;若不在图形上,对应点连线的垂直平
分线的交点就是旋转中心,旋转角等于对应点与旋
转中心所连线段的夹角.
总 结
1.如图,在直角梯形ABCD中,AD // BC,AD= 3,
BC=5,将腰DC绕点D逆时针方向旋转90°至DE,连接AE,则△ADE的面积是( )
3
课后作业
2.如图所示,已知正三角形ABC内有一点P,PA=6,PB=8,PC=10,求∠APB的大小.
分析:将△BCP绕点B逆时针旋转60°,点C和点A重合,点P旋转到点P',连接PP',得正三角形PBP',从而可知∠BPP'=60°,推出Rt△APP',求出∠APP',即可求出∠APB的大小.
2.如图所示,已知正三角形ABC内有一点P,PA=6,PB=8,PC=10,求∠APB的大小.
解:将△BCP绕点B逆时针旋转60°,点C和A重合,点P旋转到点P',连接PP'.
∵∠PBP'=60°,BP=BP',
∴△PBP'是正三角形.
∴∠BPP'=60°,P'P=BP=8.
由旋转知,AP'=PC=10,
又PA=6,∴PP'2+PA2=AP'2.
∴∠APP'=90°.
∴∠APB=60°+90°=150°.
3.如图,△ABC为等腰直角三角形,而△AFC是由△ABD按顺时针方向旋转而来的,如果BD=EC.
(1)△AFC是由△ABD旋转多少度得到的?旋转中心在哪里?
(2)∠FCE为多少度?
解:(1)△AFC是由△ABD顺时针旋转270°得到的.旋转中心是点A.
(2)∵△ABC为等腰直角三角形,
∴∠ABD=∠ACE=∠ACF=45°,
∴∠FCE=90°.
4. 如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转变换得到的.
(1)请写出旋转中心的坐标是________,旋转角是________°;
(2)以(1)中的旋转中心为中心,分别画出将△A1AC1顺时针旋转90°,180°的三角形;
(3)设Rt△ABC的两直角边BC=a,AC=b,斜边AB=c,利用变换前后所形成的图案证明勾股定理.
.
4. 如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转变换得到的.
(2)以(1)中的旋转中心为中心,分别画出将△A1AC1顺时针旋转90°,180°的三角形;
(3)设Rt△ABC的两直角边BC=a,AC=b,斜边AB=c,利用变换前后所形成的图案证明勾股定理.
(2)解:图形如图.
4. 如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转变换得到的.
(3)设Rt△ABC的两直角边BC=a,AC=b,斜边AB=c,利用变换前后所形成的图案证明勾股定理.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
