2020-2021学年华东师大版九年级下册数学 第27章 圆 达标检测卷(Word版含答案)
文档属性
| 名称 | 2020-2021学年华东师大版九年级下册数学 第27章 圆 达标检测卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 485.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 22:47:48 | ||
图片预览




文档简介
第27章达标检测卷
一、选择题(每题3分,共30分)
1.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是( )
A.点P在⊙O外
B.点P在⊙O内
C.点P在⊙O上
D.无法确定
2.如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( )
A.8 B.4 C.10 D.5
3.下列说法正确的是( )
A.三点确定一个圆
B.一个三角形只有一个外接圆
C.若点P到圆心O的距离为8 cm,圆O的直径为8 cm,则点P在圆O上
D.三角形的内心到三角形三个顶点的距离相等
4.如图,在⊙O中,CD⊥AB,则下列结论中正确的是( )
A.AC=AB B.∠C=∠BOD C.∠C=∠B D.∠A=∠BOD
5.如图,在⊙O中,弦BC=1,点A是圆上一点,且∠A=30°,则⊙O的半径是( )
A.1 B.2 C. D.
6.如图,BD为⊙O的直径,直线ED为⊙O的切线,A、C两点在圆上,AC平分∠BAD且交BD于点F.若∠ADE=19°,则∠AFB的度数是( )
A.97° B.104° C.116° D.142°
7.如图,在Rt△ABC中,∠A=90°,BC=2,以BC的中点O为圆心的圆分别与AB、AC相切于D、E两点,则的长为( )
A. B.
C.π D.2π
8.如图,△ABC内接于⊙O,D为BC上一点,E、F分别为AD、CD的中点.若⊙O的半径为1,则sin ∠ABC的值为( )
A.AD B.AC
C.EF D.CD
9.已知AC⊥BC于点C,BC=a,CA=b,AB=c,则下列选项中⊙O的半径为的是( )
10.如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切……按这样的规律进行下去,正六边形A10B10C10D10E10F10的边长为( )
A. B. C. D.
二、填空题(每题3分,共30分)
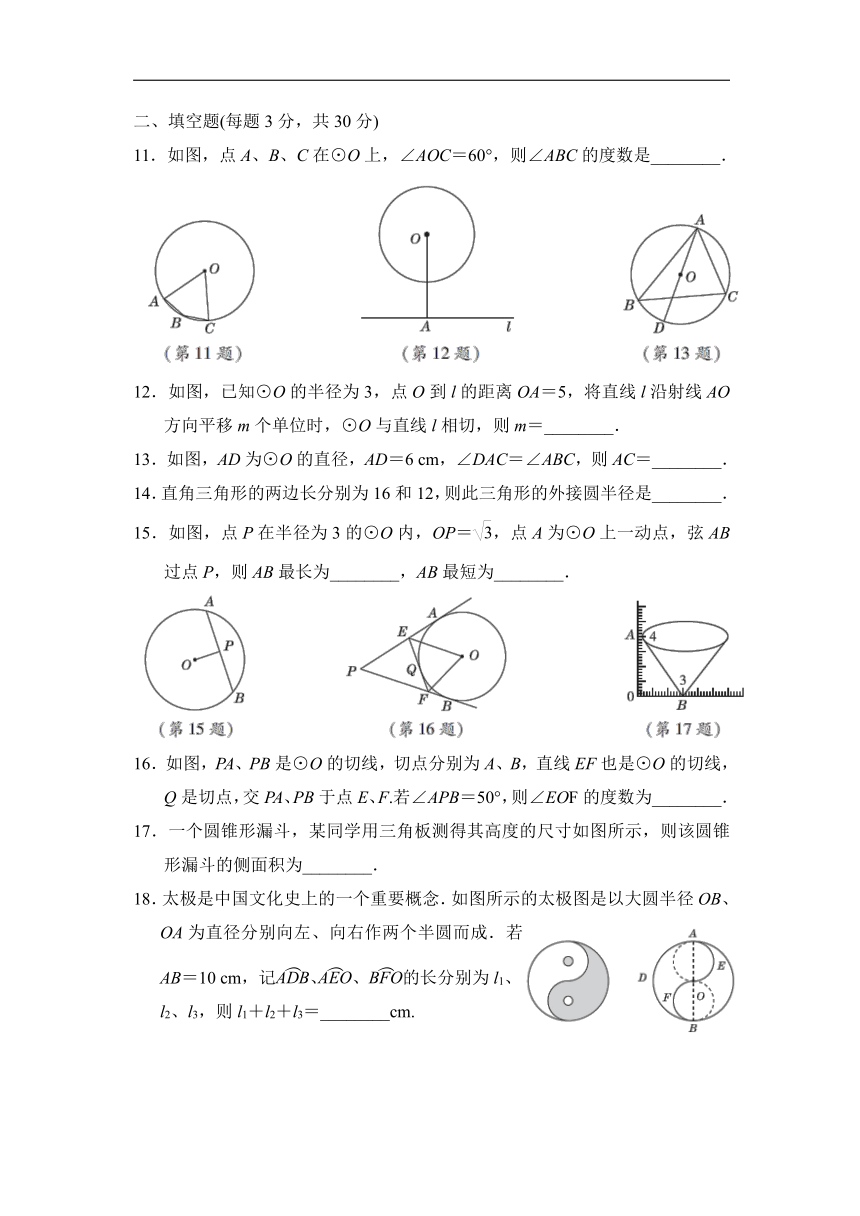
11.如图,点A、B、C在⊙O上,∠AOC=60°,则∠ABC的度数是________.
12.如图,已知⊙O的半径为3,点O到l的距离OA=5,将直线l沿射线AO方向平移m个单位时,⊙O与直线l相切,则m=________.
13.如图,AD为⊙O的直径,AD=6 cm,∠DAC=∠ABC,则AC=________.
14.直角三角形的两边长分别为16和12,则此三角形的外接圆半径是________.
15.如图,点P在半径为3的⊙O内,OP=,点A为⊙O上一动点,弦AB过点P,则AB最长为________,AB最短为________.
16.如图,PA、PB是⊙O的切线,切点分别为A、B,直线EF也是⊙O的切线,Q是切点,交PA、PB于点E、F.若∠APB=50°,则∠EOF的度数为________.
17.一个圆锥形漏斗,某同学用三角板测得其高度的尺寸如图所示,则该圆锥形漏斗的侧面积为________.
18.太极是中国文化史上的一个重要概念.如图所示的太极图是以大圆半径OB、OA为直径分别向左、向右作两个半圆而成.若AB=10 cm,记、、的长分别为l1、l2、l3,则l1+l2+l3=________cm.
19.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径是7,则GE+FH的最大值是________.
20.如图,在⊙O中,C、D分别是OA、OB的中点,MC⊥AB,ND⊥AB,M、N在⊙O上.下列结论:①MC=ND;②==;③四边形MCDN是正方形;④MN=AB,其中正确的是________.(填序号)
三、解答题(21、22题每题8分,23、24题每题10分,25、26题每题12分,共60分)
21.如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上,连结DE、BE.
(1)若∠AOD=60°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.
22.如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O于点D.已知⊙O的半径为6,∠C=40°.
(1)求∠B的度数;
(2)求的长(结果保留π).
23.如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)判断四边形AOCD是否为菱形,并说明理由.
24.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°,
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的面积.(结果保留根号和π)
25.如图,一拱形桥,圆弧形桥拱的水面跨度AB=80米,桥拱到水面的最大高度为20米.
(1)求桥拱的半径;
(2)现有一艘宽60米,顶部截面为长方形且高出水面9米的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
26.如图,AB是半圆O的直径,C是AB延长线上的点,AC的垂直平分线交半圆于点D,交AC于点E,连结DA、DC.已知半圆O的半径为3,BC=2.
(1)求AD的长;
(2)点P是线段AC上一动点,连结DP,作∠DPF=∠DAC,PF交线段CD于点F.当△DPF为等腰三角形时,求AP的长.
答案
一、1.A 2.D 3.B 4.B
5.A 点拨:本题运用数形结合思想,如图,过点B作直径BB′,连结B′C,则∠B′=30°,∠B′CB=90°,∴BC=B′B,则B′B=2×1=2,故⊙O的半径是1.
6.C
7.B 点拨:如图,连结OD、OE.设⊙O的半径为r.∵⊙O分别与AB、AC相切于D、E两点,∴OE⊥AC,OD⊥AB.∵∠A=90°,∴∠DOE=90°,OD∥AC.∵点O是BC的中点,∴OD是△ABC的中位线.∴OD=AC.∴AC=2r.同理可得AB=2r.又∵∠A=90°,AB=AC.∴∠B=45°,∵BC=2,∴由勾股定理可得AB=2,∴r=1.∴的长为=,故选B.
8.C
9.A 点拨:选项A中,如图,设⊙O的半径是x,⊙O切AC于点E,切BC于点D,切AB于点F,连结OD、OE,则四边形OECD是正方形,AE=AF,BD=BF,则a-x+b-x=c,解得x=,故A正确.选项B中,⊙O的半径r1满足=,∴r1=.选项C中,⊙O的半径r2满足=,∴r2=.选项D中,⊙O的半径r3满足a+r3=c+b-r3,
∴r3=.故选A.
10.D 点拨:∵正六边形A1B1C1D1E1F1的边长为2=,∴正六边形A2B2C2D2E2F2的外接圆的半径为,则正六边形A2B2C2D2E2F2的边长为=.
同理,正六边形A3B3C3D3E3F3的边长为=……
正六边形AnBnCnDnEnFn的边长为.当n=10时,正六边形A10B10C10D10E10F10的边长为===,故选D.
二、11.150°
12.2或8
13.3 cm
14.8或10 15.6;2 16.65°
17.15π 18.10π 19.10.5
20.①②④ 点拨:连结OM、ON,易证Rt△OMC≌Rt△OND,可得MC=ND,故①正确.在Rt△MOC中,CO=MO,得∠CMO=30°,所以∠MOC=60°,易得∠MOC=∠NOD=∠MON=60°,所以==.故②正确.易得CD=AB=OA=OM,因为MC<OM,所以MC<CD.所以四边形MCDN不是正方形.故③错误.易得MN=CD=AB,故④正确.
三、21.解:(1)∵OD⊥AB,∴=.
∴∠DEB=∠AOD=30°.
(2)在Rt△AOC中,OC=3,OA=5,由勾股定理得AC=4.
∴AB=2AC=8.
22.解:(1)∵AC切⊙O于点A,
∴∠BAC=90°.
∵∠C=40°,∴∠B=50°.
(2)如图,连结OD.∵∠B=50°,
∴∠AOD=2∠B=100°,
∴的长为=π.
23.(1)证明:如图所示,连结AC,
∵点C、D是半圆O的三等分点,
∴==,∴∠DAC=∠CAB.
∵OA=OC,∴∠CAB=∠OCA,
∴∠DAC=∠OCA,∴AE∥OC.
∴∠OCE+∠E=180°.
∵CE⊥AE,∴∠E=90°,
∴∠OCE=90°,∴OC⊥CE,
∴CE是⊙O的切线.
(2)解:四边形AOCD为菱形.理由如下:
∵=,∴∠DCA=∠CAB,
∴CD∥OA.
又∵AE∥OC,
∴四边形AOCD是平行四边形.
∵OA=OC,
∴平行四边形AOCD是菱形.
24.解:(1)相切.理由如下:
如图,连结OD.
∵AD平分∠BAC,
∴∠1=∠2.
∵OA=OD,∴∠1=∠3.
∴∠2=∠3.
∴OD∥AC.
又∵∠C=90°,
∴∠ODB=90°,即OD⊥BC.
又∵点D在⊙O上,
∴BC与⊙O相切.
(2)①设⊙O的半径为r.
∵AC=3,∠B=30°,∴AB=6.
又∵OA=OD=r,∴OB=2r.
∴2r+r=6,解得r=2,即⊙O的半径是2.
②由①得OD=2,OB=4,则BD=2 ,又易知∠DOE=60°,则S阴影=
S△OBD-S扇形DOE=×2 ×2-=2 -.
25.解:(1)如图,设点E是桥拱所在圆的圆心.
过点E作EF⊥AB于点F,延长EF交⊙E于点C,连结AE,
则CF=20米.由垂径定理知,F是AB的中点,
∴AF=FB=AB=40米.设圆的半径是r米,由勾股定理,
得AE2=AF2+EF2=AF2+(CE-CF)2,
即r2=402+(r-20)2,解得r=50.
∴桥拱的半径为50米.
(2)这艘轮船能顺利通过.理由如下:如图,设MN=60米,MN∥AB,
EC与MN的交点为D,连结EM,
易知DE⊥MN,
∴MD=30米,
∴DE===40(米).
∵EF=EC-CF=50-20=30(米),
∴DF=DE-EF=40-30=10(米).
∵10米>9米,
∴这艘轮船能顺利通过.
26.解:(1)如图①,连结OD,
∵OA=OD=OB=3,BC=2,
∴AC=8,
∵DE是AC的垂直平分线,
∴AE=AC=4,
∴OE=AE-OA=1,
在Rt△ODE中,DE==2,
在Rt△ADE中,AD==2.
(2)①当DP=DF时,如图②,点P与点A重合,点F与点C重合,则AP=0;
②当PF=DF时,如图③,则∠FDP=∠FPD,
∵∠DPF=∠DAC=∠C,
∴△DAC∽△PDC,
∴=,即=,
∴AP=5;
③当DP=PF时,如图④,则∠CDP=∠PFD,
∵∠DPF=∠DAC,
∴∠DPF=∠C,
∵∠DFP=180°-∠PDF-∠DPF,∠CPD=180°-∠C-∠CDP,
∴∠DFP=∠DPC,
∴∠CDP=∠CPD,
∴CP=CD,
∴AP=AC-CP=AC-CD=AC-AD=8-2.
综上所述,当△DPF为等腰三角形时,AP的长为0或5或8-2.
一、选择题(每题3分,共30分)
1.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是( )
A.点P在⊙O外
B.点P在⊙O内
C.点P在⊙O上
D.无法确定
2.如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( )
A.8 B.4 C.10 D.5
3.下列说法正确的是( )
A.三点确定一个圆
B.一个三角形只有一个外接圆
C.若点P到圆心O的距离为8 cm,圆O的直径为8 cm,则点P在圆O上
D.三角形的内心到三角形三个顶点的距离相等
4.如图,在⊙O中,CD⊥AB,则下列结论中正确的是( )
A.AC=AB B.∠C=∠BOD C.∠C=∠B D.∠A=∠BOD
5.如图,在⊙O中,弦BC=1,点A是圆上一点,且∠A=30°,则⊙O的半径是( )
A.1 B.2 C. D.
6.如图,BD为⊙O的直径,直线ED为⊙O的切线,A、C两点在圆上,AC平分∠BAD且交BD于点F.若∠ADE=19°,则∠AFB的度数是( )
A.97° B.104° C.116° D.142°
7.如图,在Rt△ABC中,∠A=90°,BC=2,以BC的中点O为圆心的圆分别与AB、AC相切于D、E两点,则的长为( )
A. B.
C.π D.2π
8.如图,△ABC内接于⊙O,D为BC上一点,E、F分别为AD、CD的中点.若⊙O的半径为1,则sin ∠ABC的值为( )
A.AD B.AC
C.EF D.CD
9.已知AC⊥BC于点C,BC=a,CA=b,AB=c,则下列选项中⊙O的半径为的是( )
10.如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切……按这样的规律进行下去,正六边形A10B10C10D10E10F10的边长为( )
A. B. C. D.
二、填空题(每题3分,共30分)
11.如图,点A、B、C在⊙O上,∠AOC=60°,则∠ABC的度数是________.
12.如图,已知⊙O的半径为3,点O到l的距离OA=5,将直线l沿射线AO方向平移m个单位时,⊙O与直线l相切,则m=________.
13.如图,AD为⊙O的直径,AD=6 cm,∠DAC=∠ABC,则AC=________.
14.直角三角形的两边长分别为16和12,则此三角形的外接圆半径是________.
15.如图,点P在半径为3的⊙O内,OP=,点A为⊙O上一动点,弦AB过点P,则AB最长为________,AB最短为________.
16.如图,PA、PB是⊙O的切线,切点分别为A、B,直线EF也是⊙O的切线,Q是切点,交PA、PB于点E、F.若∠APB=50°,则∠EOF的度数为________.
17.一个圆锥形漏斗,某同学用三角板测得其高度的尺寸如图所示,则该圆锥形漏斗的侧面积为________.
18.太极是中国文化史上的一个重要概念.如图所示的太极图是以大圆半径OB、OA为直径分别向左、向右作两个半圆而成.若AB=10 cm,记、、的长分别为l1、l2、l3,则l1+l2+l3=________cm.
19.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径是7,则GE+FH的最大值是________.
20.如图,在⊙O中,C、D分别是OA、OB的中点,MC⊥AB,ND⊥AB,M、N在⊙O上.下列结论:①MC=ND;②==;③四边形MCDN是正方形;④MN=AB,其中正确的是________.(填序号)
三、解答题(21、22题每题8分,23、24题每题10分,25、26题每题12分,共60分)
21.如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上,连结DE、BE.
(1)若∠AOD=60°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.
22.如图,AB是⊙O的直径,AC切⊙O于点A,BC交⊙O于点D.已知⊙O的半径为6,∠C=40°.
(1)求∠B的度数;
(2)求的长(结果保留π).
23.如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)判断四边形AOCD是否为菱形,并说明理由.
24.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°,
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的面积.(结果保留根号和π)
25.如图,一拱形桥,圆弧形桥拱的水面跨度AB=80米,桥拱到水面的最大高度为20米.
(1)求桥拱的半径;
(2)现有一艘宽60米,顶部截面为长方形且高出水面9米的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
26.如图,AB是半圆O的直径,C是AB延长线上的点,AC的垂直平分线交半圆于点D,交AC于点E,连结DA、DC.已知半圆O的半径为3,BC=2.
(1)求AD的长;
(2)点P是线段AC上一动点,连结DP,作∠DPF=∠DAC,PF交线段CD于点F.当△DPF为等腰三角形时,求AP的长.
答案
一、1.A 2.D 3.B 4.B
5.A 点拨:本题运用数形结合思想,如图,过点B作直径BB′,连结B′C,则∠B′=30°,∠B′CB=90°,∴BC=B′B,则B′B=2×1=2,故⊙O的半径是1.
6.C
7.B 点拨:如图,连结OD、OE.设⊙O的半径为r.∵⊙O分别与AB、AC相切于D、E两点,∴OE⊥AC,OD⊥AB.∵∠A=90°,∴∠DOE=90°,OD∥AC.∵点O是BC的中点,∴OD是△ABC的中位线.∴OD=AC.∴AC=2r.同理可得AB=2r.又∵∠A=90°,AB=AC.∴∠B=45°,∵BC=2,∴由勾股定理可得AB=2,∴r=1.∴的长为=,故选B.
8.C
9.A 点拨:选项A中,如图,设⊙O的半径是x,⊙O切AC于点E,切BC于点D,切AB于点F,连结OD、OE,则四边形OECD是正方形,AE=AF,BD=BF,则a-x+b-x=c,解得x=,故A正确.选项B中,⊙O的半径r1满足=,∴r1=.选项C中,⊙O的半径r2满足=,∴r2=.选项D中,⊙O的半径r3满足a+r3=c+b-r3,
∴r3=.故选A.
10.D 点拨:∵正六边形A1B1C1D1E1F1的边长为2=,∴正六边形A2B2C2D2E2F2的外接圆的半径为,则正六边形A2B2C2D2E2F2的边长为=.
同理,正六边形A3B3C3D3E3F3的边长为=……
正六边形AnBnCnDnEnFn的边长为.当n=10时,正六边形A10B10C10D10E10F10的边长为===,故选D.
二、11.150°
12.2或8
13.3 cm
14.8或10 15.6;2 16.65°
17.15π 18.10π 19.10.5
20.①②④ 点拨:连结OM、ON,易证Rt△OMC≌Rt△OND,可得MC=ND,故①正确.在Rt△MOC中,CO=MO,得∠CMO=30°,所以∠MOC=60°,易得∠MOC=∠NOD=∠MON=60°,所以==.故②正确.易得CD=AB=OA=OM,因为MC<OM,所以MC<CD.所以四边形MCDN不是正方形.故③错误.易得MN=CD=AB,故④正确.
三、21.解:(1)∵OD⊥AB,∴=.
∴∠DEB=∠AOD=30°.
(2)在Rt△AOC中,OC=3,OA=5,由勾股定理得AC=4.
∴AB=2AC=8.
22.解:(1)∵AC切⊙O于点A,
∴∠BAC=90°.
∵∠C=40°,∴∠B=50°.
(2)如图,连结OD.∵∠B=50°,
∴∠AOD=2∠B=100°,
∴的长为=π.
23.(1)证明:如图所示,连结AC,
∵点C、D是半圆O的三等分点,
∴==,∴∠DAC=∠CAB.
∵OA=OC,∴∠CAB=∠OCA,
∴∠DAC=∠OCA,∴AE∥OC.
∴∠OCE+∠E=180°.
∵CE⊥AE,∴∠E=90°,
∴∠OCE=90°,∴OC⊥CE,
∴CE是⊙O的切线.
(2)解:四边形AOCD为菱形.理由如下:
∵=,∴∠DCA=∠CAB,
∴CD∥OA.
又∵AE∥OC,
∴四边形AOCD是平行四边形.
∵OA=OC,
∴平行四边形AOCD是菱形.
24.解:(1)相切.理由如下:
如图,连结OD.
∵AD平分∠BAC,
∴∠1=∠2.
∵OA=OD,∴∠1=∠3.
∴∠2=∠3.
∴OD∥AC.
又∵∠C=90°,
∴∠ODB=90°,即OD⊥BC.
又∵点D在⊙O上,
∴BC与⊙O相切.
(2)①设⊙O的半径为r.
∵AC=3,∠B=30°,∴AB=6.
又∵OA=OD=r,∴OB=2r.
∴2r+r=6,解得r=2,即⊙O的半径是2.
②由①得OD=2,OB=4,则BD=2 ,又易知∠DOE=60°,则S阴影=
S△OBD-S扇形DOE=×2 ×2-=2 -.
25.解:(1)如图,设点E是桥拱所在圆的圆心.
过点E作EF⊥AB于点F,延长EF交⊙E于点C,连结AE,
则CF=20米.由垂径定理知,F是AB的中点,
∴AF=FB=AB=40米.设圆的半径是r米,由勾股定理,
得AE2=AF2+EF2=AF2+(CE-CF)2,
即r2=402+(r-20)2,解得r=50.
∴桥拱的半径为50米.
(2)这艘轮船能顺利通过.理由如下:如图,设MN=60米,MN∥AB,
EC与MN的交点为D,连结EM,
易知DE⊥MN,
∴MD=30米,
∴DE===40(米).
∵EF=EC-CF=50-20=30(米),
∴DF=DE-EF=40-30=10(米).
∵10米>9米,
∴这艘轮船能顺利通过.
26.解:(1)如图①,连结OD,
∵OA=OD=OB=3,BC=2,
∴AC=8,
∵DE是AC的垂直平分线,
∴AE=AC=4,
∴OE=AE-OA=1,
在Rt△ODE中,DE==2,
在Rt△ADE中,AD==2.
(2)①当DP=DF时,如图②,点P与点A重合,点F与点C重合,则AP=0;
②当PF=DF时,如图③,则∠FDP=∠FPD,
∵∠DPF=∠DAC=∠C,
∴△DAC∽△PDC,
∴=,即=,
∴AP=5;
③当DP=PF时,如图④,则∠CDP=∠PFD,
∵∠DPF=∠DAC,
∴∠DPF=∠C,
∵∠DFP=180°-∠PDF-∠DPF,∠CPD=180°-∠C-∠CDP,
∴∠DFP=∠DPC,
∴∠CDP=∠CPD,
∴CP=CD,
∴AP=AC-CP=AC-CD=AC-AD=8-2.
综上所述,当△DPF为等腰三角形时,AP的长为0或5或8-2.
