2020-2021学年沪科版九年级下册数学 期末达标检测卷(word版含答案)
文档属性
| 名称 | 2020-2021学年沪科版九年级下册数学 期末达标检测卷(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 459.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 00:00:00 | ||
图片预览


文档简介
期末达标检测卷
一、选择题(每题4分,共40分)
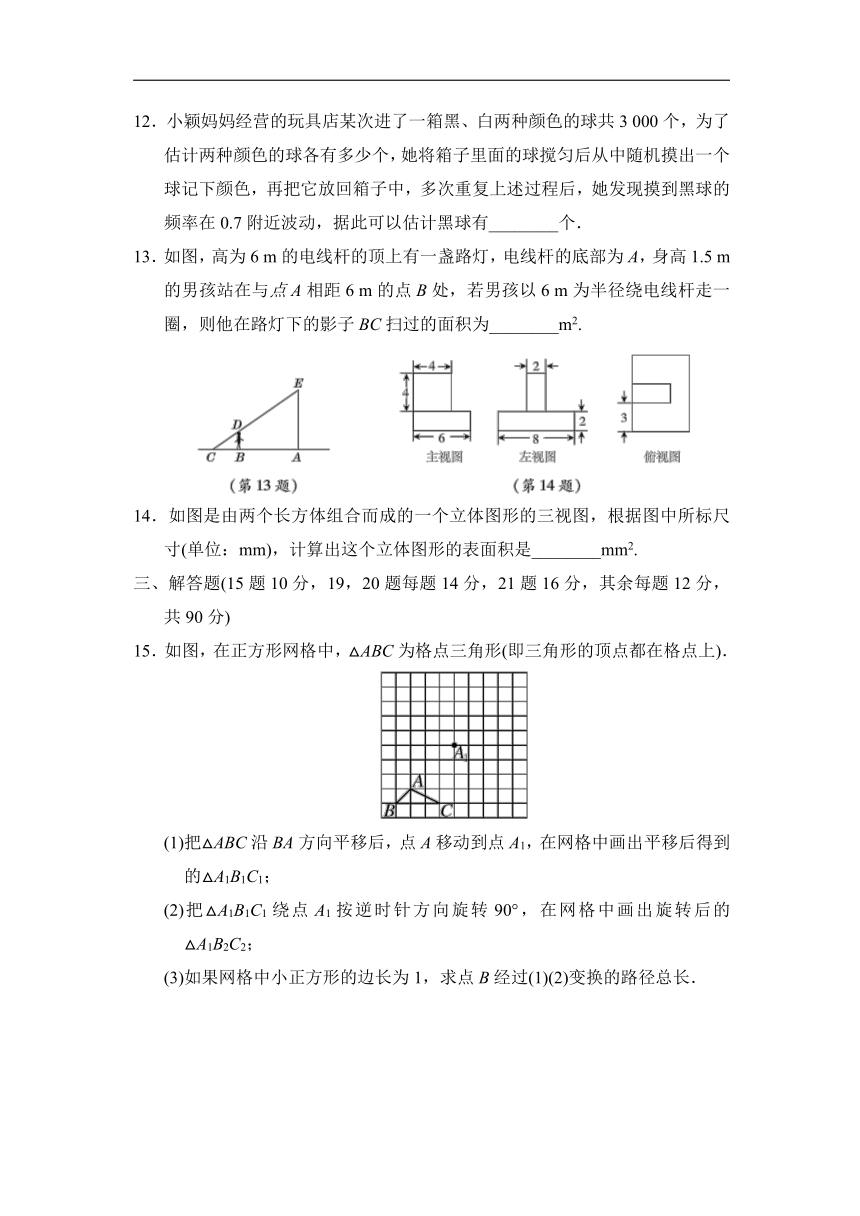
1.下列图形中,是中心对称图形的是( )
2.如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
3.下列语句所描述的事件是随机事件的是( )
A.安徽的省会是合肥
B.打开电视机,正好看到安徽卫视的节目
C.实数的绝对值小于零
D.通常温度降到0 ℃以下,纯净的水会结冰
4.如图,四边形ABCD内接于⊙O,若∠BOD=160°,则∠BCD等于( )
A.160° B.100° C.80° D.20°
5.如图,为了测量学校旗杆的高度,小东用长为3.2 m的竹竿做测量工具.移动竹竿使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8 m,与旗杆相距22 m,则旗杆的高为( )
A.8.8 m B.12 m C.16 m D.20 m
6.如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于D.已知cos∠ACD=,BC=4,则AC的长为( )
A.1 B. C.3 D.
7.九(4)班第三学习小组共有8名学生,其中女生3名,男生5名,如果从中随机选择1名学生参加学校举行的国学经典演讲比赛,那么选到女生的概率是( )
A. B. C. D.
8.如图,空心卷筒纸的高度为12 cm,外径(直径)为10 cm,内径为4 cm,在比例尺为1?4的三视图中,其主视图的面积是( )
A. cm2 B. cm2 C.30 cm2 D.7.5 cm2
9.如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( )
A.2.5 B.2.8 C.3 D.3.2
10.如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过点A的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
二、填空题(每题5分,共20分)
11.如图,AB为⊙O的直径,CD⊥AB,若AB=10,CD=8,则圆心O到弦CD的距离为________.
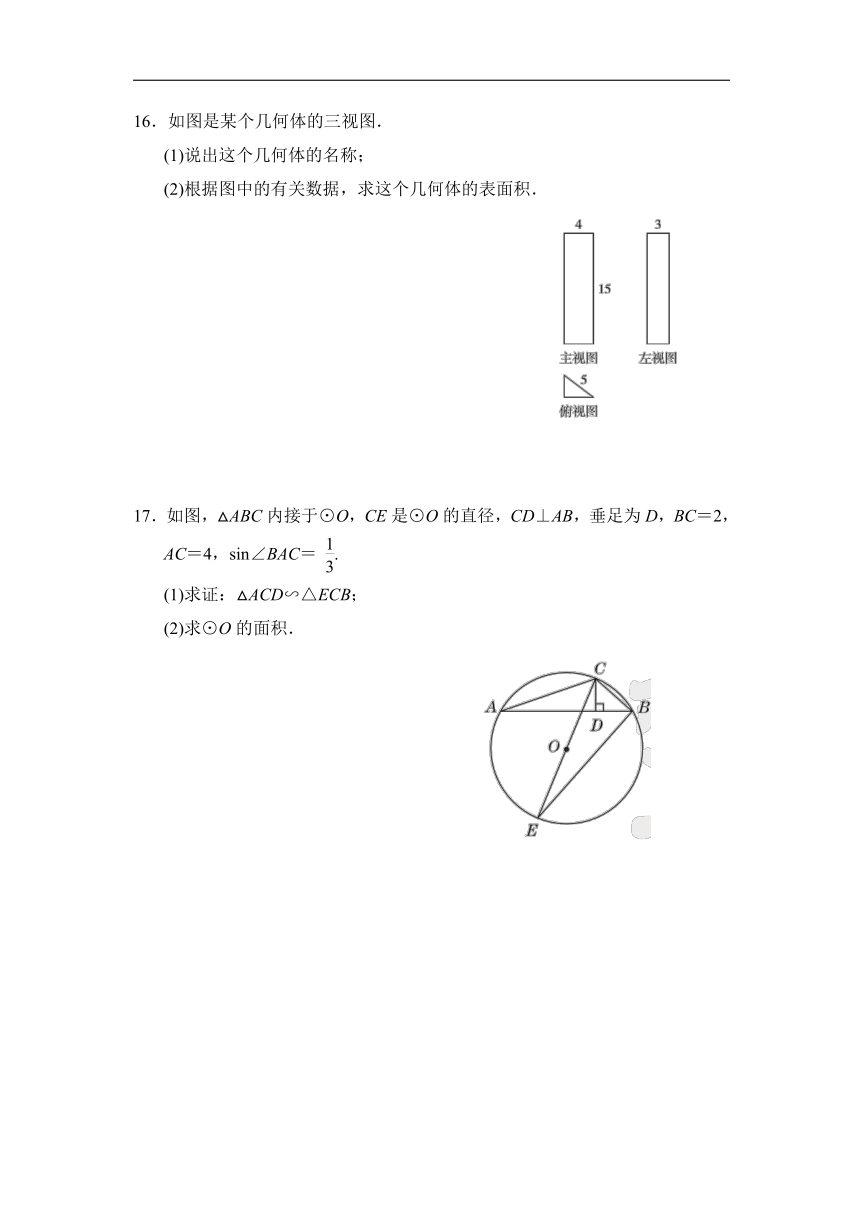
12.小颖妈妈经营的玩具店某次进了一箱黑、白两种颜色的球共3 000个,为了估计两种颜色的球各有多少个,她将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到黑球的频率在0.7附近波动,据此可以估计黑球有________个.
13.如图,高为6 m的电线杆的顶上有一盏路灯,电线杆的底部为A,身高1.5 m的男孩站在与点A相距6 m的点B处,若男孩以6 m为半径绕电线杆走一圈,则他在路灯下的影子BC扫过的面积为________m2.
14.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),计算出这个立体图形的表面积是________mm2.
三、解答题(15题10分,19,20题每题14分,21题16分,其余每题12分,共90分)
15.如图,在正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移动到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)(2)变换的路径总长.
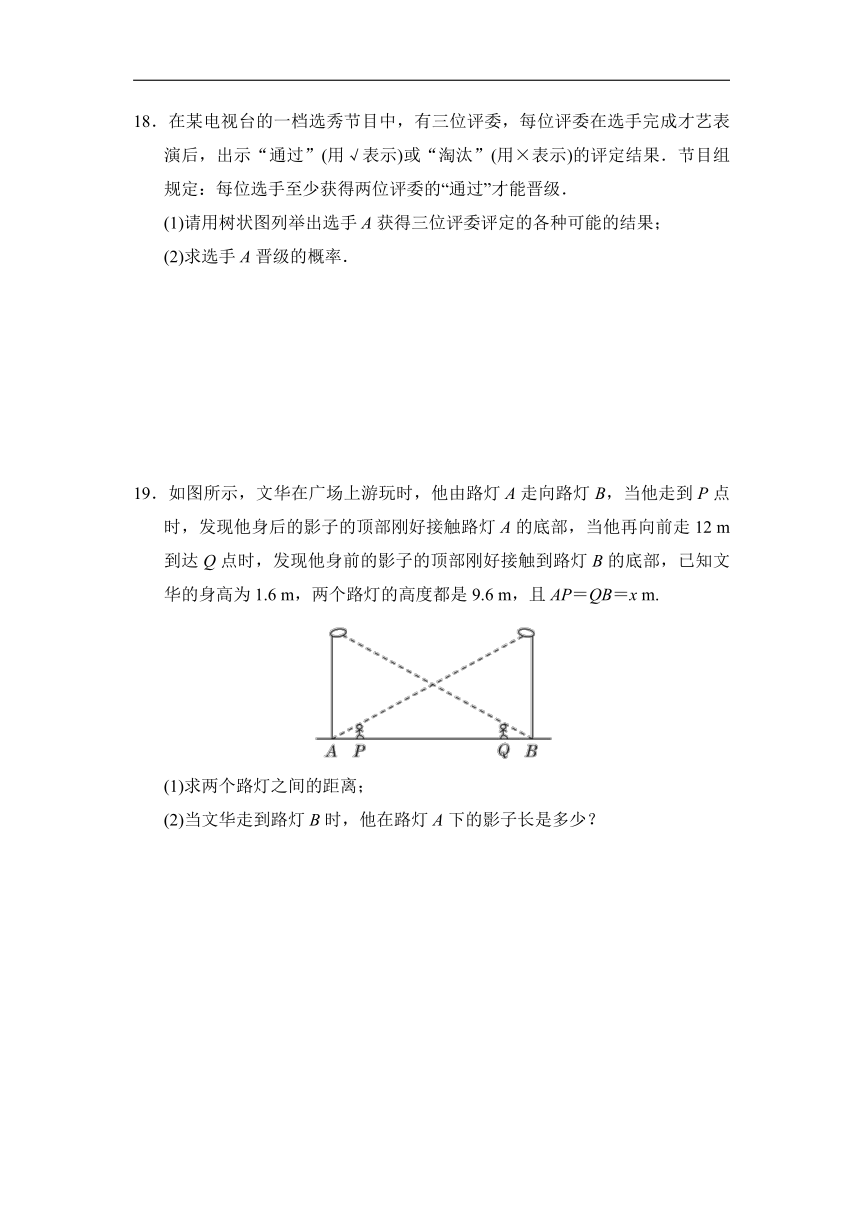
16.如图是某个几何体的三视图.
(1)说出这个几何体的名称;
(2)根据图中的有关数据,求这个几何体的表面积.
17.如图,△ABC内接于⊙O,CE是⊙O的直径,CD⊥AB,垂足为D,BC=2,AC=4,sin∠BAC= .
(1)求证:△ACD∽△ECB;
(2)求⊙O的面积.
18.在某电视台的一档选秀节目中,有三位评委,每位评委在选手完成才艺表演后,出示“通过”(用√表示)或“淘汰”(用×表示)的评定结果.节目组规定:每位选手至少获得两位评委的“通过”才能晋级.
(1)请用树状图列举出选手A获得三位评委评定的各种可能的结果;
(2)求选手A晋级的概率.
19.如图所示,文华在广场上游玩时,他由路灯A走向路灯B,当他走到P点时,发现他身后的影子的顶部刚好接触路灯A的底部,当他再向前走12 m到达Q点时,发现他身前的影子的顶部刚好接触到路灯B的底部,已知文华的身高为1.6 m,两个路灯的高度都是9.6 m,且AP=QB=x m.
(1)求两个路灯之间的距离;
(2)当文华走到路灯B时,他在路灯A下的影子长是多少?
20.如图,AB为半圆O的直径,AC是⊙O的一条弦,D为的中点,作DE⊥AC,交AC的延长线于点E,交AB的延长线于点F,连接DA.
(1)求证:EF为半圆O的切线;
(2)若DA=DF=6,求阴影区域的面积.(结果保留根号和π)
21.如图,在矩形ABCD中,AD=a cm,AB=b cm(a>b>4),半径为2 cm的⊙O在矩形内且与AB,AD均相切.现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动;⊙O在矩形内部沿AD向右匀速平移,移动到与CD相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动.已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).
(1)如图①,点P沿着A→B→C→D的方向匀速移动,全程共移动了______cm.(用含a,b的代数式表示)
(2)如图①,已知点P从A点出发,移动2 s到达B点,继续移动3 s,到达BC的中点.若点P与⊙O的移动速度相等,求在这5 s时间内圆心O移动的距离.
(3)如图②,已知a=20,b=10.是否存在如下情形:当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),PD与⊙O1恰好相切?请说明理由.
答案
一、1.A 2.A 3.B 4.B 5. B
6.D 点拨:∵AB为直径,∴∠ACB=90°,∴∠ACD+∠BCD=90°,∵CD⊥AB,∴∠BCD+∠B=90°,∴∠B=∠ACD,∵cos∠ACD=,∴cos B=,易知tan B=,∵BC=4,∴tan B===,∴AC=.
7.C
8.D 点拨:12×=3(cm),
10×=2.5(cm),
3×2.5=7.5(cm2),
即其主视图的面积是7.5 cm2.
9.B 点拨:连接BD,∵AD平分∠BAC,∴∠CAE=∠DAB,∴=.∵AB是⊙O的直径,∴∠ACE=∠ADB=90°,∴△ACE∽△ADB,∴=,即=.设AC=5x,则AE=6x,∴DE=5-6x.连接OD交BC于点F,则DO⊥BC,∴OD∥AC,易知OF=AC=x,∴DF=OD-OF=3-x,易得△ACE∽△DFE,
∴=,即=,
解得x=(x=0舍去),
则AE=6x=2.8.
10.D
二、11.3
12.2 100
13.28π
14.200 点拨:由三视图可知立体图形由上下两个长方体构成,上面长方体长4 mm,宽2 mm,高4 mm,下面长方体长8 mm,宽6 mm,高2 mm,去掉重合部分,立体图形表面积为6×8×2+8×2×2+6×2×2+4×4×2+4×2×2=200(mm2).
三、15.解:(1)如图.
(2)如图.
(3)如图,点B经过的路径为线段BB1和,∴点B经过的路径总长为+=3 +.
16.解:(1)直三棱柱.
(2)表面积为×3×4×2+15×3+15×4+15×5=192.
17. (1)证明:∵∠CAD和∠CEB都为所对的圆周角,
∴∠CAD=∠CEB.
∵CD⊥AB,∴∠CDA=90°,
∵CE为⊙O的直径,∴∠CBE=90°,
∴∠CDA=∠CBE,∴△ACD ∽△ECB.
(2)解:在Rt△ACD中,sin∠BAC==,∵AC=4,∴CD=AC=.
∵△ACD ∽△ECB,∴=,即=,∴EC=6,
∴⊙O的半径为3,∴⊙O的面积为9π.
点拨:解题的关键是利用三角形相似的判定证得三角形相似,第(1)题的结论可以作为第(2)题的条件.
18.解:(1)画树状图如图:
(2)由(1)可知共有8种等可能的结果,其中晋级的有4种情况,
所以P(A晋级)==.
19.解:(1)由题意可知,PQ=12 m,AB=(12+2x)m.
易知=,即=,解得x=3.∴AB=18 m.
即两个路灯之间的距离为18 m.
(2)设当文华走到路灯B时,他在路灯A下的影子长是a m,则 =,
解得a=3.6.
∴他在路灯A下的影子长是3.6 m.
20.(1)证明:如图,连接OD,
∵D为的中点,∴=.
∴∠EAD=∠DAO.
∵OA=OD,∴∠DAO=∠ODA.
∴∠ODA=∠EAD.
∴OD∥AE.
∵DE⊥AC,∴DE⊥OD.
∴EF是半圆O的切线.
(2)解:如图,连接OC,CD.
∵DA=DF,∴∠DAF=∠F.
又由(1)知∠CAD=∠DAF,
∴∠F=∠DAF=∠CAD.
∵∠EAF+∠F=90°,
∴3∠F=90°.
∴∠F=30°.
∴∠BAC=60°.
又∵OC=OA,
∴△OAC为等边三角形.
∴∠AOC=60°.
由(1)知OD⊥EF,
∴∠DOF=90°-∠F=60°.
在Rt△DOF中,DF=6,
∴OD=DF·tan 30°=6×=6.
在Rt△AED中,DA=6,∠CAD=30°,∴DE=DA=3,
EA=DA·cos 30°=9.
∵∠COD=180°-∠AOC-∠DOF=60°,OC=OD,
∴△COD是等边三角形.
∴∠DCO=60°=∠AOC.
∴CD∥AB.
∴S△ACD=S△COD.
∴S阴影=S△AED-S扇形COD=×9×3-=-6π.
21.解:(1)(a+2b)
(2)∵在整个运动过程中,点P移动的距离为(a+2b) cm,圆心O移动的距离为2(a-4) cm.
由题意,得a+2b=2(a-4). ①
∵点P移动2 s到达B点,即点P用2 s移动了b cm,
点P继续移动3 s,到达BC的中点,即点P用3 s移动了a cm,
∴=. ②
由①②解得
∵点P移动的速度与⊙O移动的速度相等,
∴⊙O移动的速度为=4(cm/s).
∴在这5 s时间内圆心O移动的距离为5×4=20(cm).
(3)存在这种情形.理由如下:
设点P移动的速度为v1 cm/s,
⊙O移动的速度为v2 cm/s,
由题意,得===.
如图,作直线OO1,设直线OO1与AB交于点E,与CD交于点F,⊙O1与AD相切于点G,连接O1G,则O1G⊥AD.
若PD与⊙O1相切,设切点为H,连接O1H,则O1H⊥DP,O1G=O1H,
易得Rt△DO1G≌Rt△DO1H,
∴∠ADB=∠BDP.
∵BC∥AD,
∴∠ADB=∠CBD.
∴∠BDP=∠CBD,
∴BP=DP,
设BP=x cm,则DP=x cm,PC=(20-x) cm,
在Rt△PCD中,由勾股定理,可得PC2+CD2=PD2,
即(20-x)2+102=x2,
解得x=.
∴此时点P移动的距离为10+=(cm),易知EF∥AD,
∴△BEO1∽△BAD,
∴=,即=,
∴EO1=16 cm,
∴OO1=14 cm.
(i)当⊙O首次到达⊙O1的位置时,⊙O移动的距离为14 cm,
此时点P与⊙O移动的速度比为=,
∵≠,
∴此时PD与⊙O1不可能相切.
(ii)当⊙O在返回途中到达⊙O1的位置时,⊙O移动的距离为2×(20-4)-14=18(cm),
此时点P与⊙O移动的速度比为==,
∴此时PD与⊙O1恰好相切.
一、选择题(每题4分,共40分)
1.下列图形中,是中心对称图形的是( )
2.如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
3.下列语句所描述的事件是随机事件的是( )
A.安徽的省会是合肥
B.打开电视机,正好看到安徽卫视的节目
C.实数的绝对值小于零
D.通常温度降到0 ℃以下,纯净的水会结冰
4.如图,四边形ABCD内接于⊙O,若∠BOD=160°,则∠BCD等于( )
A.160° B.100° C.80° D.20°
5.如图,为了测量学校旗杆的高度,小东用长为3.2 m的竹竿做测量工具.移动竹竿使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8 m,与旗杆相距22 m,则旗杆的高为( )
A.8.8 m B.12 m C.16 m D.20 m
6.如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于D.已知cos∠ACD=,BC=4,则AC的长为( )
A.1 B. C.3 D.
7.九(4)班第三学习小组共有8名学生,其中女生3名,男生5名,如果从中随机选择1名学生参加学校举行的国学经典演讲比赛,那么选到女生的概率是( )
A. B. C. D.
8.如图,空心卷筒纸的高度为12 cm,外径(直径)为10 cm,内径为4 cm,在比例尺为1?4的三视图中,其主视图的面积是( )
A. cm2 B. cm2 C.30 cm2 D.7.5 cm2
9.如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( )
A.2.5 B.2.8 C.3 D.3.2
10.如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过点A的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
二、填空题(每题5分,共20分)
11.如图,AB为⊙O的直径,CD⊥AB,若AB=10,CD=8,则圆心O到弦CD的距离为________.
12.小颖妈妈经营的玩具店某次进了一箱黑、白两种颜色的球共3 000个,为了估计两种颜色的球各有多少个,她将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到黑球的频率在0.7附近波动,据此可以估计黑球有________个.
13.如图,高为6 m的电线杆的顶上有一盏路灯,电线杆的底部为A,身高1.5 m的男孩站在与点A相距6 m的点B处,若男孩以6 m为半径绕电线杆走一圈,则他在路灯下的影子BC扫过的面积为________m2.
14.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),计算出这个立体图形的表面积是________mm2.
三、解答题(15题10分,19,20题每题14分,21题16分,其余每题12分,共90分)
15.如图,在正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移动到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)(2)变换的路径总长.
16.如图是某个几何体的三视图.
(1)说出这个几何体的名称;
(2)根据图中的有关数据,求这个几何体的表面积.
17.如图,△ABC内接于⊙O,CE是⊙O的直径,CD⊥AB,垂足为D,BC=2,AC=4,sin∠BAC= .
(1)求证:△ACD∽△ECB;
(2)求⊙O的面积.
18.在某电视台的一档选秀节目中,有三位评委,每位评委在选手完成才艺表演后,出示“通过”(用√表示)或“淘汰”(用×表示)的评定结果.节目组规定:每位选手至少获得两位评委的“通过”才能晋级.
(1)请用树状图列举出选手A获得三位评委评定的各种可能的结果;
(2)求选手A晋级的概率.
19.如图所示,文华在广场上游玩时,他由路灯A走向路灯B,当他走到P点时,发现他身后的影子的顶部刚好接触路灯A的底部,当他再向前走12 m到达Q点时,发现他身前的影子的顶部刚好接触到路灯B的底部,已知文华的身高为1.6 m,两个路灯的高度都是9.6 m,且AP=QB=x m.
(1)求两个路灯之间的距离;
(2)当文华走到路灯B时,他在路灯A下的影子长是多少?
20.如图,AB为半圆O的直径,AC是⊙O的一条弦,D为的中点,作DE⊥AC,交AC的延长线于点E,交AB的延长线于点F,连接DA.
(1)求证:EF为半圆O的切线;
(2)若DA=DF=6,求阴影区域的面积.(结果保留根号和π)
21.如图,在矩形ABCD中,AD=a cm,AB=b cm(a>b>4),半径为2 cm的⊙O在矩形内且与AB,AD均相切.现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动;⊙O在矩形内部沿AD向右匀速平移,移动到与CD相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动.已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).
(1)如图①,点P沿着A→B→C→D的方向匀速移动,全程共移动了______cm.(用含a,b的代数式表示)
(2)如图①,已知点P从A点出发,移动2 s到达B点,继续移动3 s,到达BC的中点.若点P与⊙O的移动速度相等,求在这5 s时间内圆心O移动的距离.
(3)如图②,已知a=20,b=10.是否存在如下情形:当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),PD与⊙O1恰好相切?请说明理由.
答案
一、1.A 2.A 3.B 4.B 5. B
6.D 点拨:∵AB为直径,∴∠ACB=90°,∴∠ACD+∠BCD=90°,∵CD⊥AB,∴∠BCD+∠B=90°,∴∠B=∠ACD,∵cos∠ACD=,∴cos B=,易知tan B=,∵BC=4,∴tan B===,∴AC=.
7.C
8.D 点拨:12×=3(cm),
10×=2.5(cm),
3×2.5=7.5(cm2),
即其主视图的面积是7.5 cm2.
9.B 点拨:连接BD,∵AD平分∠BAC,∴∠CAE=∠DAB,∴=.∵AB是⊙O的直径,∴∠ACE=∠ADB=90°,∴△ACE∽△ADB,∴=,即=.设AC=5x,则AE=6x,∴DE=5-6x.连接OD交BC于点F,则DO⊥BC,∴OD∥AC,易知OF=AC=x,∴DF=OD-OF=3-x,易得△ACE∽△DFE,
∴=,即=,
解得x=(x=0舍去),
则AE=6x=2.8.
10.D
二、11.3
12.2 100
13.28π
14.200 点拨:由三视图可知立体图形由上下两个长方体构成,上面长方体长4 mm,宽2 mm,高4 mm,下面长方体长8 mm,宽6 mm,高2 mm,去掉重合部分,立体图形表面积为6×8×2+8×2×2+6×2×2+4×4×2+4×2×2=200(mm2).
三、15.解:(1)如图.
(2)如图.
(3)如图,点B经过的路径为线段BB1和,∴点B经过的路径总长为+=3 +.
16.解:(1)直三棱柱.
(2)表面积为×3×4×2+15×3+15×4+15×5=192.
17. (1)证明:∵∠CAD和∠CEB都为所对的圆周角,
∴∠CAD=∠CEB.
∵CD⊥AB,∴∠CDA=90°,
∵CE为⊙O的直径,∴∠CBE=90°,
∴∠CDA=∠CBE,∴△ACD ∽△ECB.
(2)解:在Rt△ACD中,sin∠BAC==,∵AC=4,∴CD=AC=.
∵△ACD ∽△ECB,∴=,即=,∴EC=6,
∴⊙O的半径为3,∴⊙O的面积为9π.
点拨:解题的关键是利用三角形相似的判定证得三角形相似,第(1)题的结论可以作为第(2)题的条件.
18.解:(1)画树状图如图:
(2)由(1)可知共有8种等可能的结果,其中晋级的有4种情况,
所以P(A晋级)==.
19.解:(1)由题意可知,PQ=12 m,AB=(12+2x)m.
易知=,即=,解得x=3.∴AB=18 m.
即两个路灯之间的距离为18 m.
(2)设当文华走到路灯B时,他在路灯A下的影子长是a m,则 =,
解得a=3.6.
∴他在路灯A下的影子长是3.6 m.
20.(1)证明:如图,连接OD,
∵D为的中点,∴=.
∴∠EAD=∠DAO.
∵OA=OD,∴∠DAO=∠ODA.
∴∠ODA=∠EAD.
∴OD∥AE.
∵DE⊥AC,∴DE⊥OD.
∴EF是半圆O的切线.
(2)解:如图,连接OC,CD.
∵DA=DF,∴∠DAF=∠F.
又由(1)知∠CAD=∠DAF,
∴∠F=∠DAF=∠CAD.
∵∠EAF+∠F=90°,
∴3∠F=90°.
∴∠F=30°.
∴∠BAC=60°.
又∵OC=OA,
∴△OAC为等边三角形.
∴∠AOC=60°.
由(1)知OD⊥EF,
∴∠DOF=90°-∠F=60°.
在Rt△DOF中,DF=6,
∴OD=DF·tan 30°=6×=6.
在Rt△AED中,DA=6,∠CAD=30°,∴DE=DA=3,
EA=DA·cos 30°=9.
∵∠COD=180°-∠AOC-∠DOF=60°,OC=OD,
∴△COD是等边三角形.
∴∠DCO=60°=∠AOC.
∴CD∥AB.
∴S△ACD=S△COD.
∴S阴影=S△AED-S扇形COD=×9×3-=-6π.
21.解:(1)(a+2b)
(2)∵在整个运动过程中,点P移动的距离为(a+2b) cm,圆心O移动的距离为2(a-4) cm.
由题意,得a+2b=2(a-4). ①
∵点P移动2 s到达B点,即点P用2 s移动了b cm,
点P继续移动3 s,到达BC的中点,即点P用3 s移动了a cm,
∴=. ②
由①②解得
∵点P移动的速度与⊙O移动的速度相等,
∴⊙O移动的速度为=4(cm/s).
∴在这5 s时间内圆心O移动的距离为5×4=20(cm).
(3)存在这种情形.理由如下:
设点P移动的速度为v1 cm/s,
⊙O移动的速度为v2 cm/s,
由题意,得===.
如图,作直线OO1,设直线OO1与AB交于点E,与CD交于点F,⊙O1与AD相切于点G,连接O1G,则O1G⊥AD.
若PD与⊙O1相切,设切点为H,连接O1H,则O1H⊥DP,O1G=O1H,
易得Rt△DO1G≌Rt△DO1H,
∴∠ADB=∠BDP.
∵BC∥AD,
∴∠ADB=∠CBD.
∴∠BDP=∠CBD,
∴BP=DP,
设BP=x cm,则DP=x cm,PC=(20-x) cm,
在Rt△PCD中,由勾股定理,可得PC2+CD2=PD2,
即(20-x)2+102=x2,
解得x=.
∴此时点P移动的距离为10+=(cm),易知EF∥AD,
∴△BEO1∽△BAD,
∴=,即=,
∴EO1=16 cm,
∴OO1=14 cm.
(i)当⊙O首次到达⊙O1的位置时,⊙O移动的距离为14 cm,
此时点P与⊙O移动的速度比为=,
∵≠,
∴此时PD与⊙O1不可能相切.
(ii)当⊙O在返回途中到达⊙O1的位置时,⊙O移动的距离为2×(20-4)-14=18(cm),
此时点P与⊙O移动的速度比为==,
∴此时PD与⊙O1恰好相切.
同课章节目录
