2020-2021学年沪科版九年级下册数学 第26章 概率初步 达标检测卷(word版含答案)
文档属性
| 名称 | 2020-2021学年沪科版九年级下册数学 第26章 概率初步 达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 365.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 23:26:20 | ||
图片预览



文档简介
第26章达标检测卷
一、选择题(每题4分,共40分)
1.下列事件中,属于不可能事件的是( )
A.滴水成冰 B.水落石出 C.守株待兔 D.水中捞月
2.张志伟同学的班里共有45名学生,其中男生28人,女生17人,张老师想从中任意选取一名学生当数学课代表,则下列事件发生的可能性最大的是( )
A.选到张志伟 B.选到一名男生
C.选到一名女生 D.选到张志伟的同桌
3.不透明的袋子中有2个红球和4个蓝球,这些球除颜色外无其他差别,从袋子中随机取出1个球是红球的概率是( )
A. B. C. D.
4. 用如图所示的两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是( )
A. B. C. D.
5.某人做投硬币试验时,投掷m次,正面朝上n次(即正面朝上的频率P=),则下列说法正确的是( )
A.P一定等于 B.P一定不等于
C.多投一次,P更接近 D.投掷次数逐渐增加,P稳定在附近
6.在-1,1,2中任取两个数作为点的坐标,那么该点刚好在一次函数y=x-2的图象上的概率是( )
A. B. C. D.
7.有编号为Ⅰ,Ⅱ,Ⅲ的3个信封,现将编号为Ⅰ,Ⅱ的两封信随机地放入其中两个信封里,则信封与信的编号都相同的概率为( )
A. B. C. D.
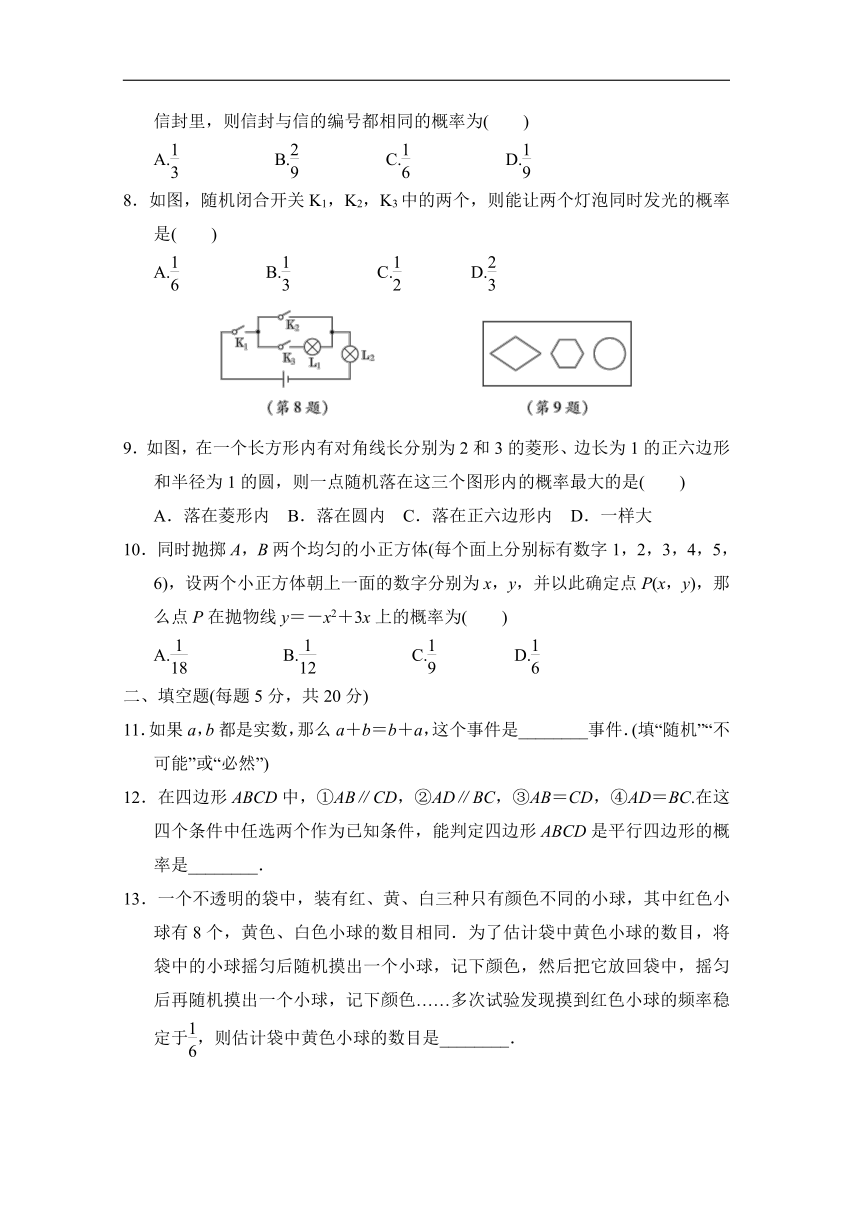
8.如图,随机闭合开关K1,K2,K3中的两个,则能让两个灯泡同时发光的概率是( )
A. B. C. D.
9.如图,在一个长方形内有对角线长分别为2和3的菱形、边长为1的正六边形和半径为1的圆,则一点随机落在这三个图形内的概率最大的是( )
A.落在菱形内 B.落在圆内 C.落在正六边形内 D.一样大
10.同时抛掷A,B两个均匀的小正方体(每个面上分别标有数字1,2,3,4,5,6),设两个小正方体朝上一面的数字分别为x,y,并以此确定点P(x,y),那么点P在抛物线y=-x2+3x上的概率为( )
A. B. C. D.
二、填空题(每题5分,共20分)
11.如果a,b都是实数,那么a+b=b+a,这个事件是________事件.(填“随机”“不可能”或“必然”)
12.在四边形ABCD中,①AB∥CD,②AD∥BC,③AB=CD,④AD=BC.在这四个条件中任选两个作为已知条件,能判定四边形ABCD是平行四边形的概率是________.
13.一个不透明的袋中,装有红、黄、白三种只有颜色不同的小球,其中红色小球有8个,黄色、白色小球的数目相同.为了估计袋中黄色小球的数目,将袋中的小球摇匀后随机摸出一个小球,记下颜色,然后把它放回袋中,摇匀后再随机摸出一个小球,记下颜色……多次试验发现摸到红色小球的频率稳定于,则估计袋中黄色小球的数目是________.
14.从-3,-2,-1,0,4这五个数中随机抽取一个数记为a,a的值既是不等式组的解,又在函数y=的自变量取值范围内的概率是________.
三、解答题(16题10分,19,20题每题14分,21题16分,其余每题12分,共90分)
15.掷两个普通的正方体骰子,把两个骰子的点数相加,请问:下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件?并说明理由.
(1)和为1;(2)和为4;(3)和为12;(4)和小于14.
16.在一次大规模的统计中发现英文文献中字母E使用的频率在0.105附近,而字母J使用的频率大约为0.001,如果这次统计是可信的,那么下列说法正确吗?试说明理由 .
(1)在英文文献中字母E出现的概率在10.5%左右,字母J出现的概率在0.1%左右;
(2)如果再去统计一篇约含200个字母的英文文献,那么字母E出现的概率一定会非常接近10.5%.
17.在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,若A为必然事件,则m的值为________,若A为随机事件,则m的值为________;
(2)若从袋子中随机摸出2个球,正好红球、黑球各1个,求这个事件发生的概率.
18.某人的钱包内有10元、20元和50元的纸币各1张,从中随机取出2张纸币.
(1)求取出纸币的总额是30元的概率;
(2)求取出纸币的总额可购买一件51元的商品的概率.
19.如图所示,有A,B两个大小均匀的转盘,其中A转盘被分成3等份,B转盘被分成4等份,并在每一份内标上数.小明和小红同时各转动其中一个转盘,转盘停止后(当指针指在边界线时视为无效,重转),若将A转盘指针指向的数记作一次函数表达式中的k,将B转盘指针指向的数记作一次函数表达式中的b.
(1)请用列表或画树状图的方法写出所有的可能;
(2)求一次函数y=kx+b的图象经过第一、二、四象限的概率.
20.某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分为100分)分成四类,并制作了统计表和统计图(如图).
根据图表信息,回答下列问题:
(1)该班共有学生________名,表中a=________;
(2)将丁类的五名学生分别记为A,B,C,D,E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方法,求B能参加决赛的概率.
21.从一副52张(没有大、小王)的扑克牌中,每次抽出1张,然后放回洗匀再抽,在试验中得到下表中部分数据:
(1)将上表补充完整.
(2)从上表中可以估计出现方块的概率是________.(精确到0.01)
(3)从这副扑克牌中取出两组牌,分别是方块1,2,3和红桃1,2,3,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,若摸出的两张牌的牌面数字之和等于3,则甲方赢;若摸出的两张牌的牌面数字之和等于4,则乙方赢.你认为这个游戏对双方是公平的吗?若不是,有利于谁?请你用概率知识(列表法或画树状图法)加以分析说明.
答案
一、1.D 2.B 3.A 4.D 5.D 6.D
7.C 8.B 9.B
10.A 点拨:列表:
B A 1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
共有36种等可能的情况,点P(x,y)在抛物线y=-x2+3x上的情况有(1,2),(2,2)2种.
∴点P在抛物线y=-x2+3x上的概率为=.
二、11.必然 12. 13.20个
14. 点拨:不等式组的解集为-<x<,函数y=的自变量的取值范围是x≠0且x≠-1.在所给的五个数-3,-2,-1,0,4中,-3与-2既满足-<x<,又满足x≠0且x≠-1,故所求概率为.
三、15.解:(4)是必然事件,(1)是不可能事件,(2)(3)是随机事件.理由如下:
最小的和为2,所以(1)是不可能事件;
和为2到12之间(包括2和12)的任意一个整数,所以(2)(3)是随机事件;
和最大为12,所以(4)是必然事件.
16.解:(1)正确,理由:当试验次数很大时可以用频率估计概率.
(2)不正确,理由:当试验次数不够大时,频率不一定接近概率.
17.解:(1)3;2
(2)画树状图如图所示:
由树状图可知,共有20种等可能的情况,从袋子中随机摸出2个球,正好红球、黑球各1个的情况有12种,∴从袋子中随机摸出2个球,正好红球、黑球各1个的概率为=.
18.解:某人从钱包内随机取出2张纸币,可能出现的结果有3种,即10元与20元,10元与50元,20元与50元,并且它们出现的可能性相等.
(1)取出纸币的总额是30元(记为事件A)的结果有1种,即10元与20元,所以P(A)=.
(2)取出纸币的总额可购买一件51元的商品(记为事件B)的结果有2种,即10元与50元,20元与50元,所以P(B)=.
19.解:(1)列表如下:
k b -1 -2 3
-1 (-1,-1) (-2,-1) (3,-1)
-2 (-1,-2) (-2,-2) (3,-2)
3 (-1,3) (-2,3) (3,3)
4 (-1,4) (-2,4) (3,4)
(2)由表格可知,所有等可能的情况有12种.一次函数y=kx+b的图象经过第一、二、四象限时,k<0,b>0,有4种情况,则P(一次函数y=kx+b的图象经过第一、二、四象限)==.
20.解:(1)40;20.
(2)列表:
所以B能参加决赛的概率为=.
21.解:(1)30;0.250 (2)0.25
(3)列表如下:
方块 红桃 1 2 3
1 (1,1) (2,1) (3,1)
2 (1,2) (2,2) (3,2)
3 (1,3) (2,3) (3,3)
所有等可能的结果有9种,其中甲方赢的结果有2种,乙方赢的结果有3种,∴P(甲方赢)=,P(乙方赢)==,∴P(乙方赢)>P(甲方赢).∴这个游戏对双方是不公平的,有利于乙方.
一、选择题(每题4分,共40分)
1.下列事件中,属于不可能事件的是( )
A.滴水成冰 B.水落石出 C.守株待兔 D.水中捞月
2.张志伟同学的班里共有45名学生,其中男生28人,女生17人,张老师想从中任意选取一名学生当数学课代表,则下列事件发生的可能性最大的是( )
A.选到张志伟 B.选到一名男生
C.选到一名女生 D.选到张志伟的同桌
3.不透明的袋子中有2个红球和4个蓝球,这些球除颜色外无其他差别,从袋子中随机取出1个球是红球的概率是( )
A. B. C. D.
4. 用如图所示的两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是( )
A. B. C. D.
5.某人做投硬币试验时,投掷m次,正面朝上n次(即正面朝上的频率P=),则下列说法正确的是( )
A.P一定等于 B.P一定不等于
C.多投一次,P更接近 D.投掷次数逐渐增加,P稳定在附近
6.在-1,1,2中任取两个数作为点的坐标,那么该点刚好在一次函数y=x-2的图象上的概率是( )
A. B. C. D.
7.有编号为Ⅰ,Ⅱ,Ⅲ的3个信封,现将编号为Ⅰ,Ⅱ的两封信随机地放入其中两个信封里,则信封与信的编号都相同的概率为( )
A. B. C. D.
8.如图,随机闭合开关K1,K2,K3中的两个,则能让两个灯泡同时发光的概率是( )
A. B. C. D.
9.如图,在一个长方形内有对角线长分别为2和3的菱形、边长为1的正六边形和半径为1的圆,则一点随机落在这三个图形内的概率最大的是( )
A.落在菱形内 B.落在圆内 C.落在正六边形内 D.一样大
10.同时抛掷A,B两个均匀的小正方体(每个面上分别标有数字1,2,3,4,5,6),设两个小正方体朝上一面的数字分别为x,y,并以此确定点P(x,y),那么点P在抛物线y=-x2+3x上的概率为( )
A. B. C. D.
二、填空题(每题5分,共20分)
11.如果a,b都是实数,那么a+b=b+a,这个事件是________事件.(填“随机”“不可能”或“必然”)
12.在四边形ABCD中,①AB∥CD,②AD∥BC,③AB=CD,④AD=BC.在这四个条件中任选两个作为已知条件,能判定四边形ABCD是平行四边形的概率是________.
13.一个不透明的袋中,装有红、黄、白三种只有颜色不同的小球,其中红色小球有8个,黄色、白色小球的数目相同.为了估计袋中黄色小球的数目,将袋中的小球摇匀后随机摸出一个小球,记下颜色,然后把它放回袋中,摇匀后再随机摸出一个小球,记下颜色……多次试验发现摸到红色小球的频率稳定于,则估计袋中黄色小球的数目是________.
14.从-3,-2,-1,0,4这五个数中随机抽取一个数记为a,a的值既是不等式组的解,又在函数y=的自变量取值范围内的概率是________.
三、解答题(16题10分,19,20题每题14分,21题16分,其余每题12分,共90分)
15.掷两个普通的正方体骰子,把两个骰子的点数相加,请问:下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件?并说明理由.
(1)和为1;(2)和为4;(3)和为12;(4)和小于14.
16.在一次大规模的统计中发现英文文献中字母E使用的频率在0.105附近,而字母J使用的频率大约为0.001,如果这次统计是可信的,那么下列说法正确吗?试说明理由 .
(1)在英文文献中字母E出现的概率在10.5%左右,字母J出现的概率在0.1%左右;
(2)如果再去统计一篇约含200个字母的英文文献,那么字母E出现的概率一定会非常接近10.5%.
17.在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,若A为必然事件,则m的值为________,若A为随机事件,则m的值为________;
(2)若从袋子中随机摸出2个球,正好红球、黑球各1个,求这个事件发生的概率.
18.某人的钱包内有10元、20元和50元的纸币各1张,从中随机取出2张纸币.
(1)求取出纸币的总额是30元的概率;
(2)求取出纸币的总额可购买一件51元的商品的概率.
19.如图所示,有A,B两个大小均匀的转盘,其中A转盘被分成3等份,B转盘被分成4等份,并在每一份内标上数.小明和小红同时各转动其中一个转盘,转盘停止后(当指针指在边界线时视为无效,重转),若将A转盘指针指向的数记作一次函数表达式中的k,将B转盘指针指向的数记作一次函数表达式中的b.
(1)请用列表或画树状图的方法写出所有的可能;
(2)求一次函数y=kx+b的图象经过第一、二、四象限的概率.
20.某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分为100分)分成四类,并制作了统计表和统计图(如图).
根据图表信息,回答下列问题:
(1)该班共有学生________名,表中a=________;
(2)将丁类的五名学生分别记为A,B,C,D,E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方法,求B能参加决赛的概率.
21.从一副52张(没有大、小王)的扑克牌中,每次抽出1张,然后放回洗匀再抽,在试验中得到下表中部分数据:
(1)将上表补充完整.
(2)从上表中可以估计出现方块的概率是________.(精确到0.01)
(3)从这副扑克牌中取出两组牌,分别是方块1,2,3和红桃1,2,3,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,若摸出的两张牌的牌面数字之和等于3,则甲方赢;若摸出的两张牌的牌面数字之和等于4,则乙方赢.你认为这个游戏对双方是公平的吗?若不是,有利于谁?请你用概率知识(列表法或画树状图法)加以分析说明.
答案
一、1.D 2.B 3.A 4.D 5.D 6.D
7.C 8.B 9.B
10.A 点拨:列表:
B A 1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
共有36种等可能的情况,点P(x,y)在抛物线y=-x2+3x上的情况有(1,2),(2,2)2种.
∴点P在抛物线y=-x2+3x上的概率为=.
二、11.必然 12. 13.20个
14. 点拨:不等式组的解集为-<x<,函数y=的自变量的取值范围是x≠0且x≠-1.在所给的五个数-3,-2,-1,0,4中,-3与-2既满足-<x<,又满足x≠0且x≠-1,故所求概率为.
三、15.解:(4)是必然事件,(1)是不可能事件,(2)(3)是随机事件.理由如下:
最小的和为2,所以(1)是不可能事件;
和为2到12之间(包括2和12)的任意一个整数,所以(2)(3)是随机事件;
和最大为12,所以(4)是必然事件.
16.解:(1)正确,理由:当试验次数很大时可以用频率估计概率.
(2)不正确,理由:当试验次数不够大时,频率不一定接近概率.
17.解:(1)3;2
(2)画树状图如图所示:
由树状图可知,共有20种等可能的情况,从袋子中随机摸出2个球,正好红球、黑球各1个的情况有12种,∴从袋子中随机摸出2个球,正好红球、黑球各1个的概率为=.
18.解:某人从钱包内随机取出2张纸币,可能出现的结果有3种,即10元与20元,10元与50元,20元与50元,并且它们出现的可能性相等.
(1)取出纸币的总额是30元(记为事件A)的结果有1种,即10元与20元,所以P(A)=.
(2)取出纸币的总额可购买一件51元的商品(记为事件B)的结果有2种,即10元与50元,20元与50元,所以P(B)=.
19.解:(1)列表如下:
k b -1 -2 3
-1 (-1,-1) (-2,-1) (3,-1)
-2 (-1,-2) (-2,-2) (3,-2)
3 (-1,3) (-2,3) (3,3)
4 (-1,4) (-2,4) (3,4)
(2)由表格可知,所有等可能的情况有12种.一次函数y=kx+b的图象经过第一、二、四象限时,k<0,b>0,有4种情况,则P(一次函数y=kx+b的图象经过第一、二、四象限)==.
20.解:(1)40;20.
(2)列表:
所以B能参加决赛的概率为=.
21.解:(1)30;0.250 (2)0.25
(3)列表如下:
方块 红桃 1 2 3
1 (1,1) (2,1) (3,1)
2 (1,2) (2,2) (3,2)
3 (1,3) (2,3) (3,3)
所有等可能的结果有9种,其中甲方赢的结果有2种,乙方赢的结果有3种,∴P(甲方赢)=,P(乙方赢)==,∴P(乙方赢)>P(甲方赢).∴这个游戏对双方是不公平的,有利于乙方.
