4.2.2用列举法求概率 同步练习(含解析)
文档属性
| 名称 | 4.2.2用列举法求概率 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 414.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-24 00:00:00 | ||
图片预览




文档简介
初中数学湘教版九年级下册4.2.2用列举法求概率 同步练习
一、单选题
1.放假了,小明与小颖两家准备从红荷湿地、台儿庄古城、莲青山中选择一景点游玩,小明与小颖通过抽签方式确定景点,则两家抽到同一景点的概率是(?? )
A.?13??????????????????????????????????????????B.?16??????????????????????????????????????????C.?19??????????????????????????????????????????D.?14
2.小明将分别标有爱我中华汉字的四个小球装在一个不透明的口袋中,这些球除汉字外都相同,每次摸球前先搅拌均匀,随机摸出一球记下汉字后放回,再随机摸出一球,两次摸出的球上的汉字能组成“中华”的概率是(? )
A.?12?????????????????????????????????????????B.?18?????????????????????????????????????????C.?14?????????????????????????????????????????D.?16
3.一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数.将骰子抛掷两次,掷第一次,将朝上一面的点数记为x,掷第二次,将朝上一面的点数记为y,则点( x,y )落在直线 y=-x+5 上的概率为:
A.?118????????????????????????????????????????B.?112????????????????????????????????????????C.?19????????????????????????????????????????D.?14
4.如图,两个转盘分别自由转动一次(当指针恰好指在分界线上时重转),当停止转动时,两个转盘的指针都指向3的概率为(?? )
A.?116?????????????????????????????????????????B.?18?????????????????????????????????????????C.?14?????????????????????????????????????????D.?12
5.有编号为Ⅰ,Ⅱ,Ⅲ的3个信封,现将编号为Ⅰ,Ⅱ的两封信,随机的放入其中两个信封里,则信封与信编号都相同的概率为(?? )
A.?16??????????????????????????????????????????B.?19??????????????????????????????????????????C.?29??????????????????????????????????????????D.?13
6.某地新高考有一项“6选3”选课制,高中学生李鑫和张锋都已选了地理和生物,现在他们还需要从“物理、化学、政治、历史”四科中选一科参加考试.若这四科被选中的机会均等,则他们恰好一人选物理,另一人选化学的概率为(?? )
A.?18??????????????????????????????????????????B.?14??????????????????????????????????????????C.?38??????????????????????????????????????????D.?12
7.两道单选题都含有A、B、C、D四个选项,小明同学在不会做的情况下,两题都答对的概率是( )
A.?18?????????????????????????????????????????B.?14?????????????????????????????????????????C.?116?????????????????????????????????????????D.?38
8.为增强学生环保意识,某中学举办了环保知识竞赛,某班共有3名学生(2名男生,1名女生)获奖.老师若从获奖的3名学生中任选两名作为班级的“环保小卫士”,则恰好是一名男生、一名女生的概率为(?? )
A.?23??????????????????????????????????????????B.?12??????????????????????????????????????????C.?49??????????????????????????????????????????D.?13
9.如图,用两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是(?? )
A.?14??????????????????????????????????????????B.?13??????????????????????????????????????????C.?12??????????????????????????????????????????D.?34
10.定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“V数”,如“947”就是一个“V数”.若十位上的数字为2,则从1,3,4,5中任选两数,能与2组成“V数”得概率是(????? )
A.?14?????????????????????????????????????????B.?310?????????????????????????????????????????C.?12?????????????????????????????????????????D.?34
二、填空题
11.从数字2,3,4中任选两个数组成一个两位数,组成的数是偶数的概率是________.
12.一个不透明的口袋中装有4个除颜色外,其他都一样的小球,其中有2个黄球,2个蓝球,现从中随机摸出2个球,则这2个球为同色的概率是________.
13.小明抛掷两枚质地均匀的骰子(如图,骰子的六个面上分别刻有1到6的点数),两枚骰子朝上的点数和是7的概率是________.
14.现有A,B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A立方体朝上的数字为x、小明 掷B立方体朝上的数字为y来确定点P( x,y ),那么它们各掷一次所确定的点P落在已知抛物线 y=-x2+4x 上的概率为________.
三、综合题
15.小明和小亮玩一个游戏,游戏规则是:在三张完全相同的卡片上分别标记 4 、 5 、 6 三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则小明获胜,若抽出的两张卡片标记的数字之和为奇数,则小亮获胜.你认为这个游戏公平吗?请说明理由.
16.小明和小刚打算寒假去北京游玩,他们准备从锦州南站乘坐动车去北京,锦州南站每天开四个检票口,其中有三个电子检票口,分别记为 A , B , C ,一个人工检票口记为 D (如图).
(1)小明随机选择一个检票口进入候车大厅,那么他从电子检票口 A 进入的概率为________;
(2)若小明和小刚分别随机选择其中一个检票口进入候车大厅,请用树状图或列表法求他们选择不同电子检票口的概率.
17.2020年春季在新冠疫情的背景下,全国各大中小学纷纷开设空中课堂,学生要面对电脑等电子产品上网课,某校为了解本校学生对自己视力保护的重视程度,随机在校内调查了部分学生,调直结果分为“非常重视”“重视”“比较重视”“不重视”四类,并将结果绘制成如图所示的两幅不完整的统计图:根据图中信息,解答下列问题:
(1)在扇形统计图中,“比较重视”所占的圆心角的度数为 ? , 并补全条形统计图;
(2)该校共有学生3200人,请你估计该校对视力保护“非常重视”的学生人数;
(3)对视力“非常重视”的4人有A1 , A2两名男生,B1 , B2两名女生,若从中随机抽取两人向全校作视力保护经验交流,请利用树状图或列表法,求出恰好抽到同性别学生的概率.
18.中考是学习生涯中的第一次重要考试.每年中考前多数学生都因学习、升学的压力过大,进而引发焦虑等不良情绪.2020年中考前,我校心理咨询室为缓解学生的压力,使每个学生都能轻松应考,制定了切实可行的减压方式,并将其分为五类(A:交流谈心,B:宣泄减压,C:沙盘游戏,D:听音乐,E:其它)同学们可根据自身的情况选择其中的一项缓解压力.
(1)小明从五类方式中随机选择一项缓解压力,则选择“沙盘游戏”的概率为________.
(2)某班一学习小组的同学在课间讨论如何缓解考试压力,其中有3名以“交流谈心”缓解考试压力,1名以“宣泄减压”缓解考试压力,1名以“听音乐”缓解考试压力;李老师想从5名同学中任选两名同学进行交流.请用树状图或列表法求选中的学生恰好都是以“交流谈心”缓解考试压力的概率.
答案解析部分
一、单选题
1. A
考点:列表法与树状图法,概率公式
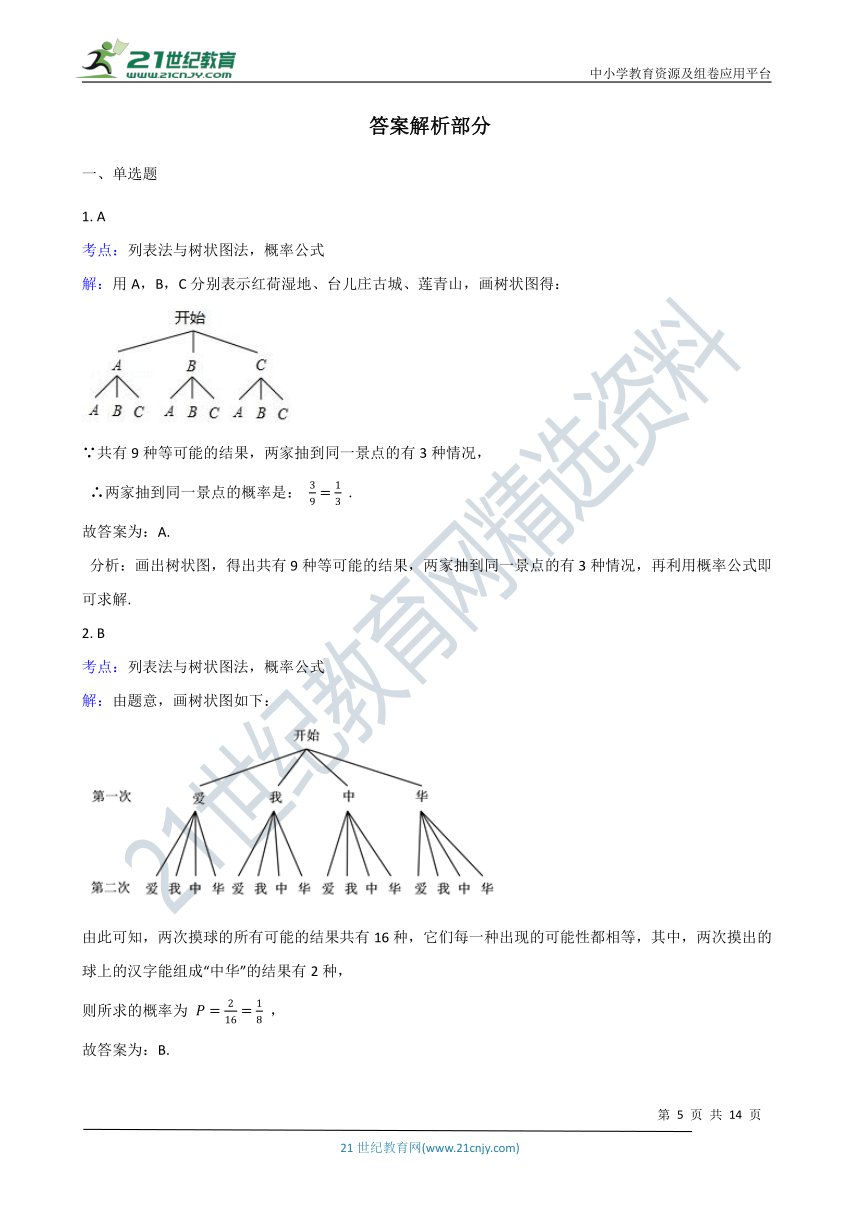
解:用A,B,C分别表示红荷湿地、台儿庄古城、莲青山,画树状图得:
∵共有9种等可能的结果,两家抽到同一景点的有3种情况,
∴两家抽到同一景点的概率是: 39=13 .
故答案为:A.
分析:画出树状图,得出共有9种等可能的结果,两家抽到同一景点的有3种情况,再利用概率公式即可求解.
2. B
考点:列表法与树状图法,概率公式
解:由题意,画树状图如下:
由此可知,两次摸球的所有可能的结果共有16种,它们每一种出现的可能性都相等,其中,两次摸出的球上的汉字能组成“中华”的结果有2种,
则所求的概率为 P=216=18 ,
故答案为:B.
分析:先画出树状图,从而可得两次摸球的所有可能的结果,再找出两次摸出的球上的汉字能组成“中华”的结果,然后利用概率公式即可得.
3. C
考点:列表法与树状图法
解:
?
1
2
3
4
5
6
1
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
2
(2,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
3
(3,1)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
4
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
(4,6)
5
(5,1)
(5,2)
(5,3)
(5,4)
(5,5)
(5,6)
6
(6,1)
(6,2)
(6,3)
(6,4)
(6,5)
(6,6)
共有36种情况,落在直线y=-x+5上的情况有(1,4)(2,3)(3,2)(4,1)4种情况,概率是 19 ,
故答案为:C.
分析:由题意列表,从表格中的信息可知所有可能的结果有36种情况,符合题意的有4种情况,再根据概率公式计算即可求解.
4. A
考点:列表法与树状图法
解:列表如下:
?
1
2
3
4
1
(1,1)
(2,1)
(3,1)
(4,1)
2
(1,2)
(2,2)
(3,2)
(4,2)
3
(1,3)
(2,3)
(3,3)
(4,3)
4
(1,4)
(2,4)
(3,4)
(4,4)
∵ 共有16种等可能的结果,两个转盘的指针都指向3的只有1种结果,
∴ 两个转盘的指针都指向3的概率为 116 ,
故答案为:A.
分析:首先根据题意列出表格,然后由表格即可求得所有等可能的结果与都指向3的情况数,继而求得答案.
5. A
考点:列表法与树状图法
解:列表如下:
信封
Ⅰ
Ⅱ
Ⅲ
信封与信编号是否都相同
信
Ⅰ
Ⅱ
空
是
信
Ⅰ
空
Ⅱ
否
信
Ⅱ
Ⅰ
空
否
信
空
Ⅰ
Ⅱ
否
信
Ⅱ
空
Ⅰ
否
信
空
Ⅱ
Ⅰ
否
由上表可知,共有6种等可能结果,其中信封与信编号都相同的只有1种结果,
∴信封与信编号都相同的概率为:16.
故答案为:A.
分析:首先根据题意用列表的方法列举出所有可能出现的结果,然后利用信封与信编号都相同的情况数除以总情况数即可求出概率.
6. A
考点:列表法与树状图法
解:如图
一共有16种结果数,但他们恰好一人选物理,另一人选化学的有2种情况,
∴P(他们恰好一人选物理,另一人选化学)=216=18.
故答案为:A.
分析:由题意可知此事件是抽取放回,列出树状图,根据树状图求出所有的可能的结果数及他们恰好一人选物理,另一人选化学的情况数,再利用概率公式进行计算.
7. C
考点:列表法与树状图法
解:据题意画图如下:
∵共有16种等情况数,两题都答对的情况有1种,
∴小明同学在不会做的情况下,两题都答对的概率 =116 .
故答案为:C.
分析:利用树状图列举出共有16种等情况数,两题都答对的情况有1种,利用概率公式计算即得.
8. A
考点:列表法与树状图法,概率公式
解:画树状图为:
?
共有6种等可能的结果数,其中抽到一名男生一名女生的结果数为4,
所以抽到一名男生一名女生的概率 46=23 ,
故答案为:A.
分析:列树状图,求出所有情况,再利用概率公式求解即可。
9. B
考点:列表法与树状图法
解:画树状图如下:
总共有6种搭配情况,其中一红一蓝的情况有2种,
所以配成紫色的概率是 P=26=13 .
故答案为:B.
分析:画出树状图,列举出所有等可能的情况数,找出能配成紫色的情况数,根据概率公式即可求出概率.
10. C
考点:列表法与树状图法
解:画树状图得:
∵可以组成的数有:321,421,521,123,423,523,124,324,524,125,325,425,
其中是“V数”的有:423,523,324,524,325,425六个,
∴从1,3,4,5中任选两数,能与2组成“V数”的概率是: 612=12 。
故答案为:C。
分析:利用树状图列举出共有12等可能结果,求出能与2组成“V数”的有6种,利用概率公式计算即可.
二、填空题
11.23
考点:列表法与树状图法
解:画树状图为:
共有6种可等可能的结果数,其中组成两位数是偶数的结果数为4,
所以组成一个两位数为偶数的概率= 46 = 23 .
故答案为 23 .
分析:画树状图展示所有6种可等可能的结果数,再找出组成两位数是偶数的结果数,然后根据概率公式求解.
12. 13
考点:列表法与树状图法
解:画树状图如图:
从中随机摸出2个球,共有12个等可能的结果,这2个球为同色的结果有4个,
∴从中随机摸出2个球,则这2个球为同色的概率是 412=13 ;
故答案为: 13 .
分析:画出树状图,得出所有各种可能的情况,然后利用概率公式即可求解.
13. 16
考点:列表法与树状图法
解:画树状图为:
共有36个等可能的结果数,其中两枚骰子朝上的点数和是7的结果数为6个,
∴两枚骰子朝上的点数和是7的概率为 636=16 ,
故答案为: 16 .
分析:画出树状图,共有36个等可能的结果数,其中两枚骰子朝上的点数和是7的结果数为6个,再由概率公式求解即可.
14. 112
考点:列表法与树状图法
解:列表如下:
y???? x
1
2
3
4
5
6
1
(1,1)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
2
(1,2)
(2,2)
(3,2)
(4,2)
(5,2)
(6,2)
3
(1,3)
(2,3)
(3,3)
(4,3)
(5,3)
(6,3)
4
(1,4)
(2,4)
(3,4)
(4,4)
(5,4)
(6,4)
5
(1,5)
(2,5)
(3,5)
(4,5)
(5,5)
(6,5)
6
(1,6)
(2,6)
(3,6)
(4,6)
(5,6)
(6,6)
点P共有36种等可能的情况,其中(1,3)、(2,4)、(3,3)三个点在抛物线y=﹣x2+4x上,
所以它们各掷一次所确定的点P落在已知抛物线y=﹣x2+4x上的概率为 336=112
故答案为 112 .
分析:根据题意列出表格可知,点P共有36种等可能的情况,而符合题意的有3个点,根据概率公式可求解.
三、综合题
15. 解:不公平,
列表如下:
4
5
6
4
8
9
10
5
9
10
11
6
10
11
12
由表可知,共有9种等可能结果,其中和为偶数的有5种结果,和为奇数的有4种结果,
所以按照游戏规则,小明获胜的概率为 59 ,小亮获胜的概率为 49 ,
由 59≠49 知这个游戏不公平;
考点:列表法与树状图法,游戏公平性
【解析】分析:首先根据题意列表,然后根据表求得所有等可能的结果与和为奇数、偶数的情况,再利用概率公式求解即可.
16. (1)14
(2)根据题意,列表格如下:
小刚
小明
A
B
C
D
A
(A,A)
(A,B)
(A,C)
(A,D)
B
(B,A)
(B,B)
(B,C)
(B,D)
C
(C,A)
(C,B)
(C,C)
(C,D)
D
(D,A)
(D,B)
(D,C)
(D,D)
由表格可知,共有16种可能的结果,每种结果出现的可能性相同,其中小明和小刚选择不同电子检票口进入候车大厅的结果有6种,即 (A,B) (A,C) (B,A) (B,C) (C,A) (C,B) ,所以 P (他们选择不同的电子检票口) =616=38 .
考点:列表法与树状图法
解:(1)∵共有四个检票口,
∴他从电子检票口 A 进入的概率为 14 .
故答案为: 14 ;
分析:(1)利用概率公式计算得出答案;(2)通过列表展示所有16种等可能结果,再找出选择不同电子检票口进入的结果数,然后根据概率公式求解.
17. (1)162°;解:“重视”的人数为80-4-36-16=24(人),补全条形统计图如图
(2)解:由题意得∶3200× 480 =160(人) ,
即估计该校对视力保护“非常重视”的学生人数为160人
(3)解:画树状图如图∶
共有12个等可能的结果,恰好抽到同性别学生的结果有4个.".恰好抽到同性别学生的概率为 412=13
考点:扇形统计图,条形统计图,列表法与树状图法
解:(1)调查的学生人数为16÷20%=80 (人),
∴“比较重视"所占的圆心角的度数为360°× 3680 =162°
故答案为∶162°.
分析:(1)用不重视的人数除以所占的百分比求出调查的人数,然后利用比较重视的人数除以总人数,再乘以360°可得所占的圆心角的度数,利用调查的人数减去非常重视、比较重视、不重视的人数,即为重视的人数,最后不全条形统计图即可;
(2)首先利用非常重视的人数除以总人数,求出所占的圆心角的度数,然后乘以该校的学生人数即可;
(3)画出树状图,找出总情况数以及恰好抽到同性别学生的结果?数,最后根据概率公式计算即可.
18. (1)15
(2)解:记3名以“交流谈心”缓解考试压力的学生分别为A1 , A2 , A3;列表如下:
A1
A2
A3
B
D
A1
(A1 , A2)
(A1 , A3)
(A1 , B)
(A1 , D)
A2
(A2 , A1)
(A2 , A3)
(A2 , B)
(A2 , D)
A3
(A3 , A1)
(A3 , A2)
(A3 , B)
(A3 , D)
B
(B,A1)
(B,A2)
(B,A3)
(B,D)
D
(D,A1)
(D,A2)
(D,A3)
(D,B)
共有20种等可能性的结果,其中恰好都是以“交流谈心”缓解考试压力的结果有6种,分别为(A2 , A1),(A3 , A1),(A1 , A2),(A3 , A2),
∴P(“交流谈心”缓解考试压力) =620=310 .
考点:列表法与树状图法,概率公式
解:(1)P(沙盘游戏)= 15 ;
分析:(1)直接根据概率公式求解即可;(2)列出表格,然后用符合条件的情况数除以所有情况的总数即可.
一、单选题
1.放假了,小明与小颖两家准备从红荷湿地、台儿庄古城、莲青山中选择一景点游玩,小明与小颖通过抽签方式确定景点,则两家抽到同一景点的概率是(?? )
A.?13??????????????????????????????????????????B.?16??????????????????????????????????????????C.?19??????????????????????????????????????????D.?14
2.小明将分别标有爱我中华汉字的四个小球装在一个不透明的口袋中,这些球除汉字外都相同,每次摸球前先搅拌均匀,随机摸出一球记下汉字后放回,再随机摸出一球,两次摸出的球上的汉字能组成“中华”的概率是(? )
A.?12?????????????????????????????????????????B.?18?????????????????????????????????????????C.?14?????????????????????????????????????????D.?16
3.一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数.将骰子抛掷两次,掷第一次,将朝上一面的点数记为x,掷第二次,将朝上一面的点数记为y,则点( x,y )落在直线 y=-x+5 上的概率为:
A.?118????????????????????????????????????????B.?112????????????????????????????????????????C.?19????????????????????????????????????????D.?14
4.如图,两个转盘分别自由转动一次(当指针恰好指在分界线上时重转),当停止转动时,两个转盘的指针都指向3的概率为(?? )
A.?116?????????????????????????????????????????B.?18?????????????????????????????????????????C.?14?????????????????????????????????????????D.?12
5.有编号为Ⅰ,Ⅱ,Ⅲ的3个信封,现将编号为Ⅰ,Ⅱ的两封信,随机的放入其中两个信封里,则信封与信编号都相同的概率为(?? )
A.?16??????????????????????????????????????????B.?19??????????????????????????????????????????C.?29??????????????????????????????????????????D.?13
6.某地新高考有一项“6选3”选课制,高中学生李鑫和张锋都已选了地理和生物,现在他们还需要从“物理、化学、政治、历史”四科中选一科参加考试.若这四科被选中的机会均等,则他们恰好一人选物理,另一人选化学的概率为(?? )
A.?18??????????????????????????????????????????B.?14??????????????????????????????????????????C.?38??????????????????????????????????????????D.?12
7.两道单选题都含有A、B、C、D四个选项,小明同学在不会做的情况下,两题都答对的概率是( )
A.?18?????????????????????????????????????????B.?14?????????????????????????????????????????C.?116?????????????????????????????????????????D.?38
8.为增强学生环保意识,某中学举办了环保知识竞赛,某班共有3名学生(2名男生,1名女生)获奖.老师若从获奖的3名学生中任选两名作为班级的“环保小卫士”,则恰好是一名男生、一名女生的概率为(?? )
A.?23??????????????????????????????????????????B.?12??????????????????????????????????????????C.?49??????????????????????????????????????????D.?13
9.如图,用两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是(?? )
A.?14??????????????????????????????????????????B.?13??????????????????????????????????????????C.?12??????????????????????????????????????????D.?34
10.定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“V数”,如“947”就是一个“V数”.若十位上的数字为2,则从1,3,4,5中任选两数,能与2组成“V数”得概率是(????? )
A.?14?????????????????????????????????????????B.?310?????????????????????????????????????????C.?12?????????????????????????????????????????D.?34
二、填空题
11.从数字2,3,4中任选两个数组成一个两位数,组成的数是偶数的概率是________.
12.一个不透明的口袋中装有4个除颜色外,其他都一样的小球,其中有2个黄球,2个蓝球,现从中随机摸出2个球,则这2个球为同色的概率是________.
13.小明抛掷两枚质地均匀的骰子(如图,骰子的六个面上分别刻有1到6的点数),两枚骰子朝上的点数和是7的概率是________.
14.现有A,B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A立方体朝上的数字为x、小明 掷B立方体朝上的数字为y来确定点P( x,y ),那么它们各掷一次所确定的点P落在已知抛物线 y=-x2+4x 上的概率为________.
三、综合题
15.小明和小亮玩一个游戏,游戏规则是:在三张完全相同的卡片上分别标记 4 、 5 、 6 三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则小明获胜,若抽出的两张卡片标记的数字之和为奇数,则小亮获胜.你认为这个游戏公平吗?请说明理由.
16.小明和小刚打算寒假去北京游玩,他们准备从锦州南站乘坐动车去北京,锦州南站每天开四个检票口,其中有三个电子检票口,分别记为 A , B , C ,一个人工检票口记为 D (如图).
(1)小明随机选择一个检票口进入候车大厅,那么他从电子检票口 A 进入的概率为________;
(2)若小明和小刚分别随机选择其中一个检票口进入候车大厅,请用树状图或列表法求他们选择不同电子检票口的概率.
17.2020年春季在新冠疫情的背景下,全国各大中小学纷纷开设空中课堂,学生要面对电脑等电子产品上网课,某校为了解本校学生对自己视力保护的重视程度,随机在校内调查了部分学生,调直结果分为“非常重视”“重视”“比较重视”“不重视”四类,并将结果绘制成如图所示的两幅不完整的统计图:根据图中信息,解答下列问题:
(1)在扇形统计图中,“比较重视”所占的圆心角的度数为 ? , 并补全条形统计图;
(2)该校共有学生3200人,请你估计该校对视力保护“非常重视”的学生人数;
(3)对视力“非常重视”的4人有A1 , A2两名男生,B1 , B2两名女生,若从中随机抽取两人向全校作视力保护经验交流,请利用树状图或列表法,求出恰好抽到同性别学生的概率.
18.中考是学习生涯中的第一次重要考试.每年中考前多数学生都因学习、升学的压力过大,进而引发焦虑等不良情绪.2020年中考前,我校心理咨询室为缓解学生的压力,使每个学生都能轻松应考,制定了切实可行的减压方式,并将其分为五类(A:交流谈心,B:宣泄减压,C:沙盘游戏,D:听音乐,E:其它)同学们可根据自身的情况选择其中的一项缓解压力.
(1)小明从五类方式中随机选择一项缓解压力,则选择“沙盘游戏”的概率为________.
(2)某班一学习小组的同学在课间讨论如何缓解考试压力,其中有3名以“交流谈心”缓解考试压力,1名以“宣泄减压”缓解考试压力,1名以“听音乐”缓解考试压力;李老师想从5名同学中任选两名同学进行交流.请用树状图或列表法求选中的学生恰好都是以“交流谈心”缓解考试压力的概率.
答案解析部分
一、单选题
1. A
考点:列表法与树状图法,概率公式
解:用A,B,C分别表示红荷湿地、台儿庄古城、莲青山,画树状图得:
∵共有9种等可能的结果,两家抽到同一景点的有3种情况,
∴两家抽到同一景点的概率是: 39=13 .
故答案为:A.
分析:画出树状图,得出共有9种等可能的结果,两家抽到同一景点的有3种情况,再利用概率公式即可求解.
2. B
考点:列表法与树状图法,概率公式
解:由题意,画树状图如下:
由此可知,两次摸球的所有可能的结果共有16种,它们每一种出现的可能性都相等,其中,两次摸出的球上的汉字能组成“中华”的结果有2种,
则所求的概率为 P=216=18 ,
故答案为:B.
分析:先画出树状图,从而可得两次摸球的所有可能的结果,再找出两次摸出的球上的汉字能组成“中华”的结果,然后利用概率公式即可得.
3. C
考点:列表法与树状图法
解:
?
1
2
3
4
5
6
1
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
2
(2,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
3
(3,1)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
4
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
(4,6)
5
(5,1)
(5,2)
(5,3)
(5,4)
(5,5)
(5,6)
6
(6,1)
(6,2)
(6,3)
(6,4)
(6,5)
(6,6)
共有36种情况,落在直线y=-x+5上的情况有(1,4)(2,3)(3,2)(4,1)4种情况,概率是 19 ,
故答案为:C.
分析:由题意列表,从表格中的信息可知所有可能的结果有36种情况,符合题意的有4种情况,再根据概率公式计算即可求解.
4. A
考点:列表法与树状图法
解:列表如下:
?
1
2
3
4
1
(1,1)
(2,1)
(3,1)
(4,1)
2
(1,2)
(2,2)
(3,2)
(4,2)
3
(1,3)
(2,3)
(3,3)
(4,3)
4
(1,4)
(2,4)
(3,4)
(4,4)
∵ 共有16种等可能的结果,两个转盘的指针都指向3的只有1种结果,
∴ 两个转盘的指针都指向3的概率为 116 ,
故答案为:A.
分析:首先根据题意列出表格,然后由表格即可求得所有等可能的结果与都指向3的情况数,继而求得答案.
5. A
考点:列表法与树状图法
解:列表如下:
信封
Ⅰ
Ⅱ
Ⅲ
信封与信编号是否都相同
信
Ⅰ
Ⅱ
空
是
信
Ⅰ
空
Ⅱ
否
信
Ⅱ
Ⅰ
空
否
信
空
Ⅰ
Ⅱ
否
信
Ⅱ
空
Ⅰ
否
信
空
Ⅱ
Ⅰ
否
由上表可知,共有6种等可能结果,其中信封与信编号都相同的只有1种结果,
∴信封与信编号都相同的概率为:16.
故答案为:A.
分析:首先根据题意用列表的方法列举出所有可能出现的结果,然后利用信封与信编号都相同的情况数除以总情况数即可求出概率.
6. A
考点:列表法与树状图法
解:如图
一共有16种结果数,但他们恰好一人选物理,另一人选化学的有2种情况,
∴P(他们恰好一人选物理,另一人选化学)=216=18.
故答案为:A.
分析:由题意可知此事件是抽取放回,列出树状图,根据树状图求出所有的可能的结果数及他们恰好一人选物理,另一人选化学的情况数,再利用概率公式进行计算.
7. C
考点:列表法与树状图法
解:据题意画图如下:
∵共有16种等情况数,两题都答对的情况有1种,
∴小明同学在不会做的情况下,两题都答对的概率 =116 .
故答案为:C.
分析:利用树状图列举出共有16种等情况数,两题都答对的情况有1种,利用概率公式计算即得.
8. A
考点:列表法与树状图法,概率公式
解:画树状图为:
?
共有6种等可能的结果数,其中抽到一名男生一名女生的结果数为4,
所以抽到一名男生一名女生的概率 46=23 ,
故答案为:A.
分析:列树状图,求出所有情况,再利用概率公式求解即可。
9. B
考点:列表法与树状图法
解:画树状图如下:
总共有6种搭配情况,其中一红一蓝的情况有2种,
所以配成紫色的概率是 P=26=13 .
故答案为:B.
分析:画出树状图,列举出所有等可能的情况数,找出能配成紫色的情况数,根据概率公式即可求出概率.
10. C
考点:列表法与树状图法
解:画树状图得:
∵可以组成的数有:321,421,521,123,423,523,124,324,524,125,325,425,
其中是“V数”的有:423,523,324,524,325,425六个,
∴从1,3,4,5中任选两数,能与2组成“V数”的概率是: 612=12 。
故答案为:C。
分析:利用树状图列举出共有12等可能结果,求出能与2组成“V数”的有6种,利用概率公式计算即可.
二、填空题
11.23
考点:列表法与树状图法
解:画树状图为:
共有6种可等可能的结果数,其中组成两位数是偶数的结果数为4,
所以组成一个两位数为偶数的概率= 46 = 23 .
故答案为 23 .
分析:画树状图展示所有6种可等可能的结果数,再找出组成两位数是偶数的结果数,然后根据概率公式求解.
12. 13
考点:列表法与树状图法
解:画树状图如图:
从中随机摸出2个球,共有12个等可能的结果,这2个球为同色的结果有4个,
∴从中随机摸出2个球,则这2个球为同色的概率是 412=13 ;
故答案为: 13 .
分析:画出树状图,得出所有各种可能的情况,然后利用概率公式即可求解.
13. 16
考点:列表法与树状图法
解:画树状图为:
共有36个等可能的结果数,其中两枚骰子朝上的点数和是7的结果数为6个,
∴两枚骰子朝上的点数和是7的概率为 636=16 ,
故答案为: 16 .
分析:画出树状图,共有36个等可能的结果数,其中两枚骰子朝上的点数和是7的结果数为6个,再由概率公式求解即可.
14. 112
考点:列表法与树状图法
解:列表如下:
y???? x
1
2
3
4
5
6
1
(1,1)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
2
(1,2)
(2,2)
(3,2)
(4,2)
(5,2)
(6,2)
3
(1,3)
(2,3)
(3,3)
(4,3)
(5,3)
(6,3)
4
(1,4)
(2,4)
(3,4)
(4,4)
(5,4)
(6,4)
5
(1,5)
(2,5)
(3,5)
(4,5)
(5,5)
(6,5)
6
(1,6)
(2,6)
(3,6)
(4,6)
(5,6)
(6,6)
点P共有36种等可能的情况,其中(1,3)、(2,4)、(3,3)三个点在抛物线y=﹣x2+4x上,
所以它们各掷一次所确定的点P落在已知抛物线y=﹣x2+4x上的概率为 336=112
故答案为 112 .
分析:根据题意列出表格可知,点P共有36种等可能的情况,而符合题意的有3个点,根据概率公式可求解.
三、综合题
15. 解:不公平,
列表如下:
4
5
6
4
8
9
10
5
9
10
11
6
10
11
12
由表可知,共有9种等可能结果,其中和为偶数的有5种结果,和为奇数的有4种结果,
所以按照游戏规则,小明获胜的概率为 59 ,小亮获胜的概率为 49 ,
由 59≠49 知这个游戏不公平;
考点:列表法与树状图法,游戏公平性
【解析】分析:首先根据题意列表,然后根据表求得所有等可能的结果与和为奇数、偶数的情况,再利用概率公式求解即可.
16. (1)14
(2)根据题意,列表格如下:
小刚
小明
A
B
C
D
A
(A,A)
(A,B)
(A,C)
(A,D)
B
(B,A)
(B,B)
(B,C)
(B,D)
C
(C,A)
(C,B)
(C,C)
(C,D)
D
(D,A)
(D,B)
(D,C)
(D,D)
由表格可知,共有16种可能的结果,每种结果出现的可能性相同,其中小明和小刚选择不同电子检票口进入候车大厅的结果有6种,即 (A,B) (A,C) (B,A) (B,C) (C,A) (C,B) ,所以 P (他们选择不同的电子检票口) =616=38 .
考点:列表法与树状图法
解:(1)∵共有四个检票口,
∴他从电子检票口 A 进入的概率为 14 .
故答案为: 14 ;
分析:(1)利用概率公式计算得出答案;(2)通过列表展示所有16种等可能结果,再找出选择不同电子检票口进入的结果数,然后根据概率公式求解.
17. (1)162°;解:“重视”的人数为80-4-36-16=24(人),补全条形统计图如图
(2)解:由题意得∶3200× 480 =160(人) ,
即估计该校对视力保护“非常重视”的学生人数为160人
(3)解:画树状图如图∶
共有12个等可能的结果,恰好抽到同性别学生的结果有4个.".恰好抽到同性别学生的概率为 412=13
考点:扇形统计图,条形统计图,列表法与树状图法
解:(1)调查的学生人数为16÷20%=80 (人),
∴“比较重视"所占的圆心角的度数为360°× 3680 =162°
故答案为∶162°.
分析:(1)用不重视的人数除以所占的百分比求出调查的人数,然后利用比较重视的人数除以总人数,再乘以360°可得所占的圆心角的度数,利用调查的人数减去非常重视、比较重视、不重视的人数,即为重视的人数,最后不全条形统计图即可;
(2)首先利用非常重视的人数除以总人数,求出所占的圆心角的度数,然后乘以该校的学生人数即可;
(3)画出树状图,找出总情况数以及恰好抽到同性别学生的结果?数,最后根据概率公式计算即可.
18. (1)15
(2)解:记3名以“交流谈心”缓解考试压力的学生分别为A1 , A2 , A3;列表如下:
A1
A2
A3
B
D
A1
(A1 , A2)
(A1 , A3)
(A1 , B)
(A1 , D)
A2
(A2 , A1)
(A2 , A3)
(A2 , B)
(A2 , D)
A3
(A3 , A1)
(A3 , A2)
(A3 , B)
(A3 , D)
B
(B,A1)
(B,A2)
(B,A3)
(B,D)
D
(D,A1)
(D,A2)
(D,A3)
(D,B)
共有20种等可能性的结果,其中恰好都是以“交流谈心”缓解考试压力的结果有6种,分别为(A2 , A1),(A3 , A1),(A1 , A2),(A3 , A2),
∴P(“交流谈心”缓解考试压力) =620=310 .
考点:列表法与树状图法,概率公式
解:(1)P(沙盘游戏)= 15 ;
分析:(1)直接根据概率公式求解即可;(2)列出表格,然后用符合条件的情况数除以所有情况的总数即可.
